Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T08:27:42.570Z Has data issue: false hasContentIssue false
  • English
  • Français

The progeny of a branching process

Published online by Cambridge University Press:  14 July 2016

R. A. Doney
R. A. Doney*
Affiliation:
Imperial College
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let {Z(t), t ≧ 0} be an age-dependent branching process with offspring generating function 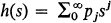and life-time distribution function G(t). Denote by N(t) the progeny of the process, that is the total number of objects which have been born in [0, t], counting the ancestor. (See Section 2 for definitions.) Then in the Galton-Watson process (i.e., when G(t) = 0 for t ≦ 1, G(t) = 1 for t > 1) we have the simple relation Nn = Z0 + Z1 + ··· + Zn, so that the asymptotic behaviour of Nn as n → ∞ follows from a knowledge of the asymptotic behaviour of Zn. In particular, if 1 < m = h'(1) < ∞ and Zn(ω)/E(Zn) → Z(ω) > 0 then also Nn(ω)/E(Nn) → Z(ω) > 0; since E(Zn)/E(Nn) → 1 – m–1 this means that

Type
Short Communications
Information
Journal of Applied Probability , Volume 8 , Issue 2 , June 1971 , pp. 407 - 412
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. (1969) On the supercritical one dimensional age dependent branching process. Ann. Math. Statist. 40, 743–763.CrossRefGoogle Scholar
[2] Harris, T. E. (1963) The Theory of Branching Processes. Springer Verlag, Berlin.Google Scholar
[3] Jagers, P. (1968) Renewal theory and the almost sure convergence of branching processes Ark. Mat. 7, 495–504.Google Scholar