Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-08T12:25:36.726Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase transition in the random triangle model

Part of: Graph theory Equilibrium statistical mechanics

Published online by Cambridge University Press:  14 July 2016

Olle Häggström  and
Johan Jonasson
Olle Häggström*
Affiliation:
Chalmers University of Technology
Johan Jonasson*
Affiliation:
Chalmers University of Technology
*
∗Postal address: Department of Mathematics, Chalmers University of Technology and Göteborg University, S41296 Göteborg, Sweden.
∗Postal address: Department of Mathematics, Chalmers University of Technology and Göteborg University, S41296 Göteborg, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

The random triangle model was recently introduced as a random graph model that captures the property of transitivity that is often found in social networks, i.e. the property that given that two vertices are second neighbors, they are more likely to be neighbors. 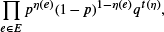For parameters p ∊ [0,1] and q ≥ 1, and a finite graph G = (V, E), it assigns to elements η of {0,1}E probabilities which are proportional to where t(η) is the number of triangles in the open subgraph. In this paper the behavior of the random triangle model on the two-dimensional triangular lattice is studied. By mapping the system onto an Ising model with external field on the hexagonal lattice, it is shown that phase transition occurs if and only if p = (q−1)−2/3 and q > qc for a critical value qc which turns out to equal 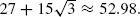It is furthermore demonstrated that phase transition cannot occur unless p = pc(q), the critical value for percolation of open edges for given q. This implies that for q ≥ qc, pc(q) = (q−1)−2/3.

Keywords

Percolationplanar dualitystochastic dominationIsing model

MSC classification

Primary: 05C80: Random graphs 82B20: Lattice systems (Ising, dimer, Potts, etc.) and systems on graphs
Type
Research Papers
Information
Journal of Applied Probability , Volume 36 , Issue 4 , December 1999 , pp. 1101 - 1115
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baxter, R. J. (1982). Exactly Solved Models in Statistical Mechanics. Academic Press, London.Google Scholar
Bollobás, B. (1985). Random Graphs. Academic Press, London.Google Scholar
Broadbent, S. R., and Hammersley, J. M. (1957). Percolation processes I. Crystals and mazes. Proc. Cambridge Phil. Soc. 53, 629–641.CrossRefGoogle Scholar
Burton, R., and Keane, M. (1989). Density and uniqueness in percolation. Commun. Math. Phys. 121, 501–505.CrossRefGoogle Scholar
Ellis, R. S. (1985). Entropy, Large Deviations and Statistical Mechanics. Springer, New York.CrossRefGoogle Scholar
Erdős, P. and Rényi, A. (1959). On random graphs I. Publ. Math. Debrecen 6, 290–297.CrossRefGoogle Scholar
Faust, K., and Wasserman, S. (1994). Social Network Analysis. CUP, Cambridge.Google Scholar
Fortuin, C. M., and Kasteleyn, P. W. (1972). On the random cluster model. I. Introduction and relation to other models. Physica 58, 393–418.CrossRefGoogle Scholar
Frank, O. (1988). Random sampling and social networks: A survey of various approaches. Math. Sci. Humaines 104, 19–33.Google Scholar
Gandolfi, A., Keane, M., and Russo, L. (1988). On the uniqueness of the infinite occupied cluster in dependent two-dimensional site percolation. Ann. Prob. 16, 1147–1157.CrossRefGoogle Scholar
Georgii, H.-O. (1988). Gibbs Measures and Phase Transitions. De Gruyter, New York.CrossRefGoogle Scholar
Grimmett, G. (1989). Percolation. Springer, New York.CrossRefGoogle Scholar
Grimmett, G. (1995). The stochastic random-cluster process and the uniqueness of random-cluster measures. Ann. Prob. 23, 1461–1510.CrossRefGoogle Scholar
Häggström, O. (1997). Ergodicity of the hard-core model on ℤ2 with parity-dependent activities. Ark. Mat. 35, 171–184.CrossRefGoogle Scholar
Häggström, O. (1998). Random-cluster representations in the study of phase transitions. Chalmers University of Technology and Göteborg University. Markov Proc. Rel. Fields 4, 275–321.Google Scholar
Holley, R. (1974). Remarks on the FKG inequalities. Commun. Math. Phys. 36, 227–231.CrossRefGoogle Scholar
Jonasson, J. (1997). The random triangle model. J. Appl. Prob. 36, 852–867.CrossRefGoogle Scholar
Jonasson, J., and Steif, J. (1999). Amenability and phase transition in the Ising model. J. Theor. Prob. 12, 549–559.CrossRefGoogle Scholar
Kotecký, R. (1994). Geometric representation of lattice models and large volume asymptotics. In Probability and Phase Transition, ed. Grimmett, G. Kluwer, Dordrecht.Google Scholar
Liggett, T. (1985). Interacting Particle Systems. Springer, New York.CrossRefGoogle Scholar
Lindvall, T. (1992). Lectures on the Coupling Method. Wiley, New York.Google Scholar
Spitzer, F. (1975). Markov random fields on an infinite tree. Ann. Prob. 3, 387–398.CrossRefGoogle Scholar
Wierman, J. C. (1981). Bond percolation on honeycomb and triangular lattices. Adv. Appl. Prob. 13, 298–313.CrossRefGoogle Scholar