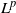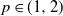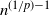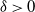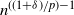1. Introduction
Let
![]() $(\mathcal{X}, \mathcal{F}_\mathcal{X}, \pi) $
be a probability space and
$(\mathcal{X}, \mathcal{F}_\mathcal{X}, \pi) $
be a probability space and
![]() $f \colon \mathcal{X} \to \mathbb{R} $
be measurable as well as
$f \colon \mathcal{X} \to \mathbb{R} $
be measurable as well as
![]() $\pi$
-integrable. For a random variable
$\pi$
-integrable. For a random variable
![]() $X\sim \pi$
we are interested in approximating the expectation
$X\sim \pi$
we are interested in approximating the expectation
A common approach is to use a Markov chain Monte Carlo (MCMC) method. Requiring the density of
![]() $\pi$
only in non-normalised form, many MCMC algorithms provide powerful tools for scientific and statistical applications. The main idea behind these approaches is to construct a Markov chain
$\pi$
only in non-normalised form, many MCMC algorithms provide powerful tools for scientific and statistical applications. The main idea behind these approaches is to construct a Markov chain
![]() $(X_n)_{n \in \mathbb{N}}$
, having
$(X_n)_{n \in \mathbb{N}}$
, having
![]() $\pi$
as the invariant distribution, and to estimate
$\pi$
as the invariant distribution, and to estimate
![]() $\pi(f)$
via
$\pi(f)$
via
 \[S_n f = \frac{1}{n}\sum_{j=1}^n f(X_j).\]
\[S_n f = \frac{1}{n}\sum_{j=1}^n f(X_j).\]
Under fairly mild conditions we have
![]() $S_n f \to \pi(f)$
almost surely as
$S_n f \to \pi(f)$
almost surely as
![]() $n \to \infty$
; cf. [Reference Asmussen and Glynn2] or [Reference Meyn and Tweedie13, Chapter 17]. This ensures the strong consistency of the MCMC estimator, yet it is clearly of interest to have non-asymptotic error bounds. For instance, given some
$n \to \infty$
; cf. [Reference Asmussen and Glynn2] or [Reference Meyn and Tweedie13, Chapter 17]. This ensures the strong consistency of the MCMC estimator, yet it is clearly of interest to have non-asymptotic error bounds. For instance, given some
![]() $p \in [1,\infty)$
, we can consider the p-mean error,
$p \in [1,\infty)$
, we can consider the p-mean error,
however, other criteria are also feasible – see, e.g., [Reference Kunsch and Rudolf9].
Setting
![]() $p=2$
in (1.1), we speak of the mean squared error, and in different settings explicit bounds are known, e.g. under a Wasserstein contraction assumption [Reference Joulin and Ollivier8], spectral gap conditions [Reference Rudolf17], or if we have geometric/polynomial ergodicity [Reference Łatuszyński, Miasojedow and Niemiro10]. For the mean squared error to make sense we require a finite second moment of f, i.e.
$p=2$
in (1.1), we speak of the mean squared error, and in different settings explicit bounds are known, e.g. under a Wasserstein contraction assumption [Reference Joulin and Ollivier8], spectral gap conditions [Reference Rudolf17], or if we have geometric/polynomial ergodicity [Reference Łatuszyński, Miasojedow and Niemiro10]. For the mean squared error to make sense we require a finite second moment of f, i.e.
![]() $\Vert f\Vert_{L^2(\pi)}^2 = \pi(f^2) \lt \infty$
. On the other hand, the absolute mean error, given by
$\Vert f\Vert_{L^2(\pi)}^2 = \pi(f^2) \lt \infty$
. On the other hand, the absolute mean error, given by
![]() $\mathbb{E} \vert S_n f - \pi (f) \vert$
, is well defined and finite as long as f is
$\mathbb{E} \vert S_n f - \pi (f) \vert$
, is well defined and finite as long as f is
![]() $\pi$
-integrable. Bounds for the absolute mean error for functions with
$\pi$
-integrable. Bounds for the absolute mean error for functions with
![]() $\Vert f\Vert_{L^p(\pi)}^p = \pi (\vert f \vert^p) \lt \infty $
, where
$\Vert f\Vert_{L^p(\pi)}^p = \pi (\vert f \vert^p) \lt \infty $
, where
![]() $p \lt 2$
, are still rare. In [Reference Rudolf and Schweizer18] it is shown that, under a spectral gap condition, for any
$p \lt 2$
, are still rare. In [Reference Rudolf and Schweizer18] it is shown that, under a spectral gap condition, for any
![]() $p \in (1,2)$
,
$p \in (1,2)$
,
with constants
![]() $\delta \gt 0$
and
$\delta \gt 0$
and
![]() $C\in (0, \infty)$
.
$C\in (0, \infty)$
.
Setting
![]() $k=0$
in [Reference Novak15, Proposition 1, Section 2.2.9] (see also [Reference Heinrich7, Section 5]) shows that in general we have the lower bound
$k=0$
in [Reference Novak15, Proposition 1, Section 2.2.9] (see also [Reference Heinrich7, Section 5]) shows that in general we have the lower bound
where
![]() $c \in (0, \infty)$
is a constant independent of n.
$c \in (0, \infty)$
is a constant independent of n.
Even though
![]() $\delta \gt 0 $
in (1.2) may be chosen arbitrarily small, it is natural to ask whether it can be removed completely, such that we would have the same rate as in (1.3). Under the (strong) assumption of uniform ergodicity and reversibility we know that this is the case; cf. [Reference Rudolf and Schweizer18, Theorem 1]. To the best of the author’s knowledge this is the only situation where optimal rates are known. The goal of this note is to extend this result to the spectral gap setting – see Theorem 2.1, where we show that
$\delta \gt 0 $
in (1.2) may be chosen arbitrarily small, it is natural to ask whether it can be removed completely, such that we would have the same rate as in (1.3). Under the (strong) assumption of uniform ergodicity and reversibility we know that this is the case; cf. [Reference Rudolf and Schweizer18, Theorem 1]. To the best of the author’s knowledge this is the only situation where optimal rates are known. The goal of this note is to extend this result to the spectral gap setting – see Theorem 2.1, where we show that
for
![]() $p \in (1,2]$
, with an explicit expression for the constant
$p \in (1,2]$
, with an explicit expression for the constant
![]() $\widetilde{C}_p$
.
$\widetilde{C}_p$
.
Let us sketch the proof. The main idea is to employ the Riesz–Thorin interpolation theorem, a technique which goes back at least to [Reference Heinrich7] in Monte Carlo theory, and was also used to derive (1.2) in [Reference Rudolf and Schweizer18]. To this end, we first derive a result for the case where
![]() $(X_n)_{n \in \mathbb{N}}$
is a stationary chain; see Proposition 3.1. Then we apply a change of measure argument to deduce Theorem 2.1. It is worth mentioning that, based on Proposition 3.1, it is also possible to generalise [Reference Rudolf17, Theorem 3.41]; see Corollary 3.1.
$(X_n)_{n \in \mathbb{N}}$
is a stationary chain; see Proposition 3.1. Then we apply a change of measure argument to deduce Theorem 2.1. It is worth mentioning that, based on Proposition 3.1, it is also possible to generalise [Reference Rudolf17, Theorem 3.41]; see Corollary 3.1.
The rest of this note is organised as follows. In Section 2 we state and discuss our assumptions, as well as the main result. The proofs, together with some intermediate results, can be found in Section 3.
2. Error bounds for MCMC integration
This section contains our main result, Theorem 2.1, together with the required notation and assumptions. Let us start by specifying the general setting.
We assume that the state space
![]() $(\mathcal{X}, \mathcal{F}_\mathcal{X})$
is Polish with
$(\mathcal{X}, \mathcal{F}_\mathcal{X})$
is Polish with
![]() $\mathcal{F}_\mathcal{X}$
being countably generated. Let K be a Markov kernel and
$\mathcal{F}_\mathcal{X}$
being countably generated. Let K be a Markov kernel and
![]() $\nu$
a probability measure, called the initial distribution, both defined on
$\nu$
a probability measure, called the initial distribution, both defined on
![]() $(\mathcal{X}, \mathcal{F}_\mathcal{X})$
. Then, the Markov chain corresponding to K and
$(\mathcal{X}, \mathcal{F}_\mathcal{X})$
. Then, the Markov chain corresponding to K and
![]() $\nu$
, say
$\nu$
, say
![]() $(X_n)_{n \in \mathbb{N}}$
, is defined on a probability space
$(X_n)_{n \in \mathbb{N}}$
, is defined on a probability space
![]() $(\Omega, \mathcal{F}, \mathbb{P}_\nu)$
. In particular, such a probability space exists. We assume that
$(\Omega, \mathcal{F}, \mathbb{P}_\nu)$
. In particular, such a probability space exists. We assume that
![]() $\pi$
is the unique invariant distribution of K and that
$\pi$
is the unique invariant distribution of K and that
![]() $(X_n)_{n \in \mathbb{N}}$
is
$(X_n)_{n \in \mathbb{N}}$
is
![]() $\psi$
-irreducible. For definitions and further details we refer to [Reference Douc, Moulines, Priouret and Soulier4, Reference Meyn and Tweedie13].
$\psi$
-irreducible. For definitions and further details we refer to [Reference Douc, Moulines, Priouret and Soulier4, Reference Meyn and Tweedie13].
Given
![]() $p \in [1, \infty)$
, we define
$p \in [1, \infty)$
, we define
![]() $L^p (\pi)$
as the set of all functions
$L^p (\pi)$
as the set of all functions
![]() $f \colon \mathcal{X} \to \mathbb{R}$
such that
$f \colon \mathcal{X} \to \mathbb{R}$
such that
![]() $\Vert f\Vert_{L^p(\pi)}^p = \pi(\vert f \vert^p) \lt \infty$
. Similarly,
$\Vert f\Vert_{L^p(\pi)}^p = \pi(\vert f \vert^p) \lt \infty$
. Similarly,
![]() $L^\infty(\pi)$
denotes the set of functions with finite
$L^\infty(\pi)$
denotes the set of functions with finite
![]() $\Vert f\Vert_{L^\infty(\pi)} = {\rm ess\,sup}_{x \in \mathcal{X}} \vert f(x) \vert$
. We follow the usual convention that two functions in
$\Vert f\Vert_{L^\infty(\pi)} = {\rm ess\,sup}_{x \in \mathcal{X}} \vert f(x) \vert$
. We follow the usual convention that two functions in
![]() $L^p(\pi)$
, with
$L^p(\pi)$
, with
![]() $p \in [1, \infty]$
, are considered as equal if they are equal
$p \in [1, \infty]$
, are considered as equal if they are equal
![]() $\pi$
-almost everywhere. Then,
$\pi$
-almost everywhere. Then,
![]() $(L^p(\pi),\Vert {\cdot}\Vert_{L^p(\pi)})$
is a normed space. Moreover,
$(L^p(\pi),\Vert {\cdot}\Vert_{L^p(\pi)})$
is a normed space. Moreover,
![]() $L^2(\pi)$
, equipped with
$L^2(\pi)$
, equipped with
![]() $\langle f, g\rangle_{L^2(\pi)} = \int_\mathcal{X} f(x) g(x)\,\pi(\mathrm{d} x)$
, is a Hilbert space with induced norm
$\langle f, g\rangle_{L^2(\pi)} = \int_\mathcal{X} f(x) g(x)\,\pi(\mathrm{d} x)$
, is a Hilbert space with induced norm
![]() $\Vert {\cdot}\Vert_{L^2(\pi)}$
, and so is the closed subspace
$\Vert {\cdot}\Vert_{L^2(\pi)}$
, and so is the closed subspace
![]() $L^2_0 (\pi) \,:\!=\, \{f \in L^2(\pi) \colon \pi(f) = 0\}$
.
$L^2_0 (\pi) \,:\!=\, \{f \in L^2(\pi) \colon \pi(f) = 0\}$
.
Let
![]() $p \in [1, \infty]$
; then the Markov kernel K induces a linear operator
$p \in [1, \infty]$
; then the Markov kernel K induces a linear operator
![]() $K\colon L^p(\pi)\to L^p(\pi)$
via
$K\colon L^p(\pi)\to L^p(\pi)$
via
![]() $f \mapsto Kf({\cdot}) = \int_\mathcal{X} f(x')\,K({\cdot}, \mathrm{d} x')$
. Indeed, the operator K is well defined and we have
$f \mapsto Kf({\cdot}) = \int_\mathcal{X} f(x')\,K({\cdot}, \mathrm{d} x')$
. Indeed, the operator K is well defined and we have
![]() $\Vert K\Vert_{L^p(\pi) \to L^p(\pi)} =1$
; we refer to [Reference Rudolf17, Section 3.1] for further details.
$\Vert K\Vert_{L^p(\pi) \to L^p(\pi)} =1$
; we refer to [Reference Rudolf17, Section 3.1] for further details.
We denote by Id the identity on
![]() $L^2(\pi)$
. The following condition about the operator
$L^2(\pi)$
. The following condition about the operator
![]() $\mathrm{Id}-K$
, restricted to
$\mathrm{Id}-K$
, restricted to
![]() $L^2_0(\pi)$
, is our main assumption.
$L^2_0(\pi)$
, is our main assumption.
Assumption 2.1.
Assume that
![]() $\mathrm{Id} - K$
, considered as an operator from
$\mathrm{Id} - K$
, considered as an operator from
![]() $L^2_0(\pi)$
to
$L^2_0(\pi)$
to
![]() $L^2_0(\pi)$
, has a linear and bounded inverse with
$L^2_0(\pi)$
, has a linear and bounded inverse with
![]() $\Vert(\mathrm{Id} - K)^{-1}\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq s \lt \infty$
.
$\Vert(\mathrm{Id} - K)^{-1}\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq s \lt \infty$
.
Remark 2.1. The invertibility of
![]() $\mathrm{Id} -K$
, restricted to a suitable subspace of
$\mathrm{Id} -K$
, restricted to a suitable subspace of
![]() $L^2(\pi)$
, was also studied in [Reference Mathé11] for uniformly ergodic chains and [Reference Mathé12] for V-uniformly ergodic chains. In particular, the existence of
$L^2(\pi)$
, was also studied in [Reference Mathé11] for uniformly ergodic chains and [Reference Mathé12] for V-uniformly ergodic chains. In particular, the existence of
![]() $(\mathrm{Id} - K)^{-1}$
on an appropriate subspace was used there to characterise the convergence behaviour of the mean squared error. Moreover, non-reversible chains on finite state spaces were studied recently in [Reference Chatterjee3]. There, bounds for the mean squared error are shown, where the second smallest singular value of
$(\mathrm{Id} - K)^{-1}$
on an appropriate subspace was used there to characterise the convergence behaviour of the mean squared error. Moreover, non-reversible chains on finite state spaces were studied recently in [Reference Chatterjee3]. There, bounds for the mean squared error are shown, where the second smallest singular value of
![]() $\mathrm{Id} -K$
plays an important role.
$\mathrm{Id} -K$
plays an important role.
We note that Assumption 2.1 is closely related to a spectral gap; there are, however, different definitions for a spectral gap:
-
• Some authors (see, e.g., [Reference Andrieu, Lee, Power and Wang1, Reference Douc, Moulines, Priouret and Soulier4]) say K admits a(n) (absolute
 $L^2$
) spectral gap if
$L^2$
) spectral gap if
 $\sup_{\lambda \in \mathcal{S}_0} \vert \lambda \vert \lt 1$
, where
$\sup_{\lambda \in \mathcal{S}_0} \vert \lambda \vert \lt 1$
, where
 $\mathcal{S}_0$
is the spectrum of
$\mathcal{S}_0$
is the spectrum of
 $K \colon L^2_0 (\pi) \to L^2_0 (\pi)$
. This is equivalent to the existence of some
$K \colon L^2_0 (\pi) \to L^2_0 (\pi)$
. This is equivalent to the existence of some
 $m \in \mathbb{N}$
such that
$m \in \mathbb{N}$
such that
 $\Vert K^m\Vert_{L^2_0(\pi) \to L^2_0(\pi)} < 1$
; cf. [Reference Douc, Moulines, Priouret and Soulier4, Proposition 22.2.4].
$\Vert K^m\Vert_{L^2_0(\pi) \to L^2_0(\pi)} < 1$
; cf. [Reference Douc, Moulines, Priouret and Soulier4, Proposition 22.2.4]. -
• On the other hand, a different definition, for instance used in [Reference Hairer, Stuart and Vollmer6, Reference Natarovskii, Rudolf and Sprungk14, Reference Rudolf17, Reference Rudolf and Schweizer18], is to say that K admits a(n) (absolute
 $L^2$
) spectral gap if
$L^2$
) spectral gap if
 $\Vert K\Vert_{L^2_0(\pi)\to L^2_0(\pi)} \lt 1$
.
$\Vert K\Vert_{L^2_0(\pi)\to L^2_0(\pi)} \lt 1$
.
If K is reversible, which implies that the corresponding Markov operator is self-adjoint on
![]() $L^2(\pi)$
, then both definitions are equivalent.
$L^2(\pi)$
, then both definitions are equivalent.
Let us emphasise that either of the above definitions of a spectral gap implies that Assumption 2.1 is true, including in the non-reversible case. Spectral gap results were established for a number of MCMC methods, see for instance [Reference Andrieu, Lee, Power and Wang1, Reference Hairer, Stuart and Vollmer6, Reference Natarovskii, Rudolf and Sprungk14]; see also [Reference Rudolf17, Section 3.4] and [Reference Roberts and Rosenthal16, Theorem 2.1]. Moreover, we note that under Assumption 2.1 we cover the setting of [Reference Rudolf and Schweizer18, Theorems 1 and 2].
If for the initial distribution we have
![]() $\nu \ll \pi$
with Radon–Nikodým derivative
$\nu \ll \pi$
with Radon–Nikodým derivative
![]() ${\mathrm{d}\nu}/{\mathrm{d}\pi} \in L^q(\pi)$
for some
${\mathrm{d}\nu}/{\mathrm{d}\pi} \in L^q(\pi)$
for some
![]() $q \in[1, \infty]$
, then we set
$q \in[1, \infty]$
, then we set
![]() $M_q = \Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^q(\pi)}$
. In particular, for
$M_q = \Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^q(\pi)}$
. In particular, for
![]() $q = \infty$
we have
$q = \infty$
we have
![]() $\sup_{A \in \mathcal{F}_\mathcal{X}}[{\nu(A)}/{\pi(A)}] \leq M_\infty$
, in which case
$\sup_{A \in \mathcal{F}_\mathcal{X}}[{\nu(A)}/{\pi(A)}] \leq M_\infty$
, in which case
![]() $\nu$
is called
$\nu$
is called
![]() $M_\infty$
-warm.
$M_\infty$
-warm.
The following theorem is our main result, which shows that under Assumption 2.1 we have the optimal rate of convergence for the absolute mean error.
Theorem 2.1.
Let Assumption 2.1
be true,
![]() $p \in (1,2]$
, and assume that
$p \in (1,2]$
, and assume that
![]() $\nu$
is absolutely continuous with respect to
$\nu$
is absolutely continuous with respect to
![]() $\pi$
with Radon–Nikodým derivative
$\pi$
with Radon–Nikodým derivative
![]() ${\mathrm{d}\nu}/{\mathrm{d}\pi} \in L^q(\pi)$
, where
${\mathrm{d}\nu}/{\mathrm{d}\pi} \in L^q(\pi)$
, where
![]() $q \gt 0$
satisfies
$q \gt 0$
satisfies
![]() $p^{-1} + q^{-1} =1$
. Then, for any
$p^{-1} + q^{-1} =1$
. Then, for any
![]() $f \in L^p(\pi)$
and any
$f \in L^p(\pi)$
and any
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
where
![]() $C_p = 2^{2/p-1} \cdot (4s)^{1-1/p}$
and
$C_p = 2^{2/p-1} \cdot (4s)^{1-1/p}$
and
![]() $M_q = \Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^q(\pi)}$
.
$M_q = \Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^q(\pi)}$
.
Remark 2.2. We note that Theorem 2.1 is still true, with the same bound, if we replace
![]() $S_nf$
by
$S_nf$
by
![]() $S_{n, n_0}f = {1}/{n}\sum_{j=1}^{n} f(X_{j+n_0})$
, which corresponds to using a burn in of length
$S_{n, n_0}f = {1}/{n}\sum_{j=1}^{n} f(X_{j+n_0})$
, which corresponds to using a burn in of length
![]() $n_0 \in \mathbb{N}$
.
$n_0 \in \mathbb{N}$
.
Remark 2.3. Let
![]() $p\in (1,2]$
,
$p\in (1,2]$
,
![]() $q \in [1, \infty)$
with
$q \in [1, \infty)$
with
![]() $p^{-1} + q^{-1}=1$
, and
$p^{-1} + q^{-1}=1$
, and
![]() $C_p, M_q$
as specified in Theorem 2.1. Given
$C_p, M_q$
as specified in Theorem 2.1. Given
![]() $c \in \mathbb{R}$
and
$c \in \mathbb{R}$
and
![]() $f \in L^p(\pi)$
, we set
$f \in L^p(\pi)$
, we set
![]() $f_c = f+c$
, and note that
$f_c = f+c$
, and note that
![]() $S_n f_c - \pi(f_c) = S_n f - \pi(f)$
. Thus, for fixed
$S_n f_c - \pi(f_c) = S_n f - \pi(f)$
. Thus, for fixed
![]() $f \in L^p(\pi)$
and any
$f \in L^p(\pi)$
and any
![]() $c \in \mathbb{R}$
we have
$c \in \mathbb{R}$
we have
even though
![]() $\Vert{\cdot}\Vert_{L^p(\pi)}$
is not invariant with respect to linear shifts.
$\Vert{\cdot}\Vert_{L^p(\pi)}$
is not invariant with respect to linear shifts.
Remark 2.4. In Theorem 2.1 the quantity
![]() $\Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^q(\pi)}$
appears. In some sense this penalises our choice of the initial distribution
$\Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^q(\pi)}$
appears. In some sense this penalises our choice of the initial distribution
![]() $\nu$
, which is allowed to differ from the target
$\nu$
, which is allowed to differ from the target
![]() $\pi$
. In the setting where a fixed computational budget is available it may be worth spending some effort to find a ‘good’ initial distribution
$\pi$
. In the setting where a fixed computational budget is available it may be worth spending some effort to find a ‘good’ initial distribution
![]() $\nu$
. However, discussing optimal choices of
$\nu$
. However, discussing optimal choices of
![]() $\nu$
with respect to different theoretical and/or practical aspects is beyond the scope of this note.
$\nu$
with respect to different theoretical and/or practical aspects is beyond the scope of this note.
3. Proofs
In this section we prove our main results. Recall that the chain
![]() $(X_n)_{n \in \mathbb{N}}$
is defined on the probability space
$(X_n)_{n \in \mathbb{N}}$
is defined on the probability space
![]() $(\Omega, \mathcal{F}, \mathbb{P}_\nu)$
. For
$(\Omega, \mathcal{F}, \mathbb{P}_\nu)$
. For
![]() $p \in [1, \infty]$
we define
$p \in [1, \infty]$
we define
![]() $L^p(\mathbb{P}_\nu)$
as the set of random variables Y on
$L^p(\mathbb{P}_\nu)$
as the set of random variables Y on
![]() $(\Omega, \mathcal{F}, \mathbb{P}_\nu)$
such that
$(\Omega, \mathcal{F}, \mathbb{P}_\nu)$
such that
![]() $\Vert Y\Vert_{L^p(\mathbb{P}_\nu)}^p = \mathbb{E}_\nu [\vert Y \vert^p] \lt \infty$
. As for the
$\Vert Y\Vert_{L^p(\mathbb{P}_\nu)}^p = \mathbb{E}_\nu [\vert Y \vert^p] \lt \infty$
. As for the
![]() $L^p(\pi)$
spaces, we consider two random variables
$L^p(\pi)$
spaces, we consider two random variables
![]() $Y_1, Y_2 \in L^p(\mathbb{P}_\nu)$
as equal if
$Y_1, Y_2 \in L^p(\mathbb{P}_\nu)$
as equal if
![]() $Y_1=Y_2$
holds
$Y_1=Y_2$
holds
![]() $\mathbb{P}_\nu$
-almost surely. Then,
$\mathbb{P}_\nu$
-almost surely. Then,
![]() $(L^p(\mathbb{P}_\nu), \Vert \cdot\Vert_{L^p(\mathbb{P}_\nu)})$
is a normed space.
$(L^p(\mathbb{P}_\nu), \Vert \cdot\Vert_{L^p(\mathbb{P}_\nu)})$
is a normed space.
The first result of this section provides a bound for the mean squared error of
![]() $S_n h$
for the case where
$S_n h$
for the case where
![]() $(X_n)_{n \in \mathbb{N}}$
is stationary, i.e. where
$(X_n)_{n \in \mathbb{N}}$
is stationary, i.e. where
![]() $X_1 \sim \pi$
, and h is a centred function.
$X_1 \sim \pi$
, and h is a centred function.
Lemma 3.1.
Let Assumption 2.1 be true and assume that
![]() $(X_n)_{n \in \mathbb{N}}$
has initial distribution
$(X_n)_{n \in \mathbb{N}}$
has initial distribution
![]() $\pi$
, i.e.
$\pi$
, i.e.
![]() $X_1 \sim \pi$
. Then, for any
$X_1 \sim \pi$
. Then, for any
![]() $h \in L^2_0(\pi)$
and any
$h \in L^2_0(\pi)$
and any
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $\mathbb{E}_\pi[\vert S_n h\vert^2] \leq ({4 s}/{n})\Vert h\Vert_{L^2(\pi)}^2$
.
$\mathbb{E}_\pi[\vert S_n h\vert^2] \leq ({4 s}/{n})\Vert h\Vert_{L^2(\pi)}^2$
.
Proof. Expanding
![]() $\mathbb{E}_\pi[\vert S_n h\vert^2]$
and using [Reference Rudolf17, Lemma 3.25], we get
$\mathbb{E}_\pi[\vert S_n h\vert^2]$
and using [Reference Rudolf17, Lemma 3.25], we get
 \[ \mathbb{E}_\pi[\vert S_n h\vert^2] = \frac{1}{n^2}\sum_{j=1}^n\sum_{k=1}^n\mathbb{E}_\pi[h(X_j)h(X_k)] = \frac{1}{n^2}\sum_{j=1}^{n}\sum_{k=1}^n\big\langle h,K^{\vert j-k\vert}h\big\rangle_{L^2(\pi)}. \]
\[ \mathbb{E}_\pi[\vert S_n h\vert^2] = \frac{1}{n^2}\sum_{j=1}^n\sum_{k=1}^n\mathbb{E}_\pi[h(X_j)h(X_k)] = \frac{1}{n^2}\sum_{j=1}^{n}\sum_{k=1}^n\big\langle h,K^{\vert j-k\vert}h\big\rangle_{L^2(\pi)}. \]
We have that
![]() $\sum_{j=1}^n\sum_{k=1}^nK^{\vert j-k\vert} = 2\sum_{\ell=1}^{n-1}(n-\ell)K^\ell + n\mathrm{Id} = 2\sum_{\ell=0}^{n-1}(n-\ell)K^\ell - n\mathrm{Id}$
. Moreover, by induction it follows that
$\sum_{j=1}^n\sum_{k=1}^nK^{\vert j-k\vert} = 2\sum_{\ell=1}^{n-1}(n-\ell)K^\ell + n\mathrm{Id} = 2\sum_{\ell=0}^{n-1}(n-\ell)K^\ell - n\mathrm{Id}$
. Moreover, by induction it follows that
![]() $\sum_{\ell=0}^{n-1}(n-\ell)K^\ell = (\mathrm{Id}-K)^{-1}\sum_{m=1}^{n}(\mathrm{Id} - K^m)$
, where all the operators are understood to act on
$\sum_{\ell=0}^{n-1}(n-\ell)K^\ell = (\mathrm{Id}-K)^{-1}\sum_{m=1}^{n}(\mathrm{Id} - K^m)$
, where all the operators are understood to act on
![]() $L^2_0(\pi)$
.
$L^2_0(\pi)$
.
Hence, again considering all operators to act on
![]() $L^2_0(\pi)$
, the following identity holds:
$L^2_0(\pi)$
, the following identity holds:
 \begin{align} \sum_{j=1}^n\sum_{k=1}^nK^{\vert j-k\vert} & = 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^{n}(\mathrm{Id} - K^m) - n\mathrm{Id} \nonumber \\ & = 2n(\mathrm{Id}-K)^{-1} - 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^n K^m - n\mathrm{Id} \nonumber \\ & = n(\mathrm{Id} - K)^{-1}(\mathrm{Id} + K) - 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^nK^m. \end{align}
\begin{align} \sum_{j=1}^n\sum_{k=1}^nK^{\vert j-k\vert} & = 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^{n}(\mathrm{Id} - K^m) - n\mathrm{Id} \nonumber \\ & = 2n(\mathrm{Id}-K)^{-1} - 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^n K^m - n\mathrm{Id} \nonumber \\ & = n(\mathrm{Id} - K)^{-1}(\mathrm{Id} + K) - 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^nK^m. \end{align}
Set
![]() $R_n =n (\mathrm{Id} - K)^{-1}(\mathrm{Id} + K) - 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^nK^m$
. By the triangle inequality and the bounds
$R_n =n (\mathrm{Id} - K)^{-1}(\mathrm{Id} + K) - 2(\mathrm{Id} - K)^{-1}\sum_{m=1}^nK^m$
. By the triangle inequality and the bounds
![]() $\Vert(\mathrm{Id}-K)^{-1}\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq s$
and
$\Vert(\mathrm{Id}-K)^{-1}\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq s$
and
![]() $\Vert K^m\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq 1$
, which are true for any
$\Vert K^m\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq 1$
, which are true for any
![]() $m \in \mathbb{N}$
, we obtain
$m \in \mathbb{N}$
, we obtain
![]() $\Vert R_n\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq 2sn + 2sn = 4sn$
. Since
$\Vert R_n\Vert_{L^2_0(\pi) \to L^2_0(\pi)} \leq 2sn + 2sn = 4sn$
. Since
![]() $\big\langle h,K^{\vert j-k\vert}h\big\rangle_{L^2(\pi)} = \big\langle h,K^{\vert j-k\vert}h\big\rangle_{L^2_0(\pi)}$
for any
$\big\langle h,K^{\vert j-k\vert}h\big\rangle_{L^2(\pi)} = \big\langle h,K^{\vert j-k\vert}h\big\rangle_{L^2_0(\pi)}$
for any
![]() $j,k \in \{1,\ldots,n\}$
, it follows from (3.1) and the bound on
$j,k \in \{1,\ldots,n\}$
, it follows from (3.1) and the bound on
![]() $\Vert R_n\Vert_{L^2_0(\pi) \to L^2_0(\pi)}$
that
$\Vert R_n\Vert_{L^2_0(\pi) \to L^2_0(\pi)}$
that
which completes the proof.
Proposition 3.1.
Let Assumption 2.1 be true, let
![]() $p \in [1, 2]$
, and assume that
$p \in [1, 2]$
, and assume that
![]() $(X_n)_{n \in \mathbb{N}}$
has initial distribution
$(X_n)_{n \in \mathbb{N}}$
has initial distribution
![]() $\pi$
, i.e.
$\pi$
, i.e.
![]() $X_1 \sim \pi$
. Then, for any
$X_1 \sim \pi$
. Then, for any
![]() $f \in L^p(\pi)$
and any
$f \in L^p(\pi)$
and any
![]() $n \in \mathbb{N}$
we have
$n \in \mathbb{N}$
we have
Proof. For any
![]() $g \in L^2(\pi)$
set
$g \in L^2(\pi)$
set
![]() $\bar{g} = g - \pi(g) \in L^2_0(\pi)$
. Moreover, we set
$\bar{g} = g - \pi(g) \in L^2_0(\pi)$
. Moreover, we set
![]() $T_n f = S_nf-\pi(f)$
for
$T_n f = S_nf-\pi(f)$
for
![]() $f \in L^p(\pi)$
with
$f \in L^p(\pi)$
with
![]() $p \in [1,2]$
.
$p \in [1,2]$
.
By Lemma 3.1 and the inequality
![]() $\Vert\bar{g}\Vert_{L^2(\pi)}^2 = \pi(g^2)-\pi(g)^2 \leq \pi(g^2) = \Vert g\Vert_{L^2(\pi)}^2$
, which is true for any
$\Vert\bar{g}\Vert_{L^2(\pi)}^2 = \pi(g^2)-\pi(g)^2 \leq \pi(g^2) = \Vert g\Vert_{L^2(\pi)}^2$
, which is true for any
![]() $g \in L^2(\pi)$
, we obtain
$g \in L^2(\pi)$
, we obtain
which implies that
![]() $\Vert T_n\Vert_{L^2(\pi) \to L^2(\mathbb{P}_\pi)} \leq \sqrt{{4s}/{n}}$
. Moreover, using the triangle inequality we see that
$\Vert T_n\Vert_{L^2(\pi) \to L^2(\mathbb{P}_\pi)} \leq \sqrt{{4s}/{n}}$
. Moreover, using the triangle inequality we see that
![]() $\Vert T_n\Vert_{L^1(\pi) \to L^1(\mathbb{P}_\pi)} \leq 2$
. Thus, by the Riesz–Thorin interpolation theorem, see [Reference Grafakos5, Theorem 1.3.4] in the setting
$\Vert T_n\Vert_{L^1(\pi) \to L^1(\mathbb{P}_\pi)} \leq 2$
. Thus, by the Riesz–Thorin interpolation theorem, see [Reference Grafakos5, Theorem 1.3.4] in the setting
![]() $p_0 = q_0 = 1$
,
$p_0 = q_0 = 1$
,
![]() $p_1 = q_1 = 2$
, and
$p_1 = q_1 = 2$
, and
![]() $\theta = 2- 2/p$
, we obtain that
$\theta = 2- 2/p$
, we obtain that
which implies the result.
Using a change of measure argument and Proposition 3.1 we are able to prove our main result. However, before we turn to the proof of Theorem 2.1 let us state another consequence of Proposition 3.1. We note that the upcoming result generalises [Reference Rudolf17, Theorem 3.41] by providing a bound for the mean squared error of
![]() $S_n f$
for
$S_n f$
for
![]() $L^2(\pi)$
functions.
$L^2(\pi)$
functions.
Corollary 3.1.
Let Assumption 2.1 be true, let
![]() $p \in [1, 2]$
, and assume that
$p \in [1, 2]$
, and assume that
![]() $\nu \ll \pi$
with Radon–Nikodým derivative
$\nu \ll \pi$
with Radon–Nikodým derivative
![]() ${\mathrm{d}\nu}/{\mathrm{d}\pi} \in L^\infty(\pi)$
. Then, for any
${\mathrm{d}\nu}/{\mathrm{d}\pi} \in L^\infty(\pi)$
. Then, for any
![]() $f \in L^p(\pi)$
and any
$f \in L^p(\pi)$
and any
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
where
![]() $C_p = 2^{2-p}\cdot(4s)^{p-1}$
and
$C_p = 2^{2-p}\cdot(4s)^{p-1}$
and
![]() $M_\infty = \Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^\infty(\pi)}$
.
$M_\infty = \Vert{\mathrm{d}\nu}/{\mathrm{d}\pi}\Vert_{L^\infty(\pi)}$
.
Proof. Since
![]() $\mathbb{P}_\nu$
and
$\mathbb{P}_\nu$
and
![]() $\mathbb{P}_\pi$
only differ by the choice of the initial distribution of
$\mathbb{P}_\pi$
only differ by the choice of the initial distribution of
![]() $(X_n)_{n \in \mathbb{N}}$
, we have
$(X_n)_{n \in \mathbb{N}}$
, we have
Hence, the result follows from Proposition 3.1.
Finally, we turn to the proof of Theorem 2.1.
Proof of Theorem 2.1. By the same change of measure argument as before and Hoelder’s inequality,
Now the desired result is a consequence of Proposition 3.1.
Acknowledgements
The author would like to thank Mareike Hasenpflug and Daniel Rudolf for valuable discussions which helped to significantly improve the presentation of the paper. Moreover, I express my gratitude to two anonymous referees for reading the paper carefully and suggesting a simplification of Section 3.
Funding information
JH is supported by the DFG within project 432680300 – SFB 1456 subproject B02.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.