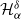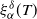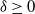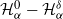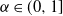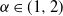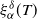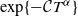1. Introduction
For any
![]() $\alpha\in(0,2]$
let
$\alpha\in(0,2]$
let
![]() $\{B_\alpha(t), t\in\mathbb{R}\}$
be a fractional Brownian motion (fBm) with Hurst parameter
$\{B_\alpha(t), t\in\mathbb{R}\}$
be a fractional Brownian motion (fBm) with Hurst parameter
![]() $H=\alpha/2$
; that is,
$H=\alpha/2$
; that is,
![]() $B_\alpha(t)$
is a centered Gaussian process with covariance function given by
$B_\alpha(t)$
is a centered Gaussian process with covariance function given by
In this manuscript we consider the classical Pickands constant defined by
The constant
![]() $\mathcal H_\alpha$
was first defined by Pickands [Reference Pickands31, Reference Pickands32] to describe the asymptotic behavior of the maximum of stationary Gaussian processes. Since then, Pickands constants have played an important role in the theory of Gaussian processes, appearing in various asymptotic results related to the supremum; see the monographs [Reference Piterbarg33, Reference Piterbarg34]. In [Reference Dieker and Mikosch22], it was recognized that the discrete Pickands constant can be interpreted as an extremal index of a Brown–Resnick process. This new realization motivated the generalization of Pickands constants beyond the realm of Gaussian processes. For further references the reader may consult [Reference Dębicki, Engelke and Hashorva13, Reference Dębicki and Hashorva14], which give an excellent account of the history of Pickands constants, their connection to the theory of max-stable processes, and the most recent advances in the theory.
$\mathcal H_\alpha$
was first defined by Pickands [Reference Pickands31, Reference Pickands32] to describe the asymptotic behavior of the maximum of stationary Gaussian processes. Since then, Pickands constants have played an important role in the theory of Gaussian processes, appearing in various asymptotic results related to the supremum; see the monographs [Reference Piterbarg33, Reference Piterbarg34]. In [Reference Dieker and Mikosch22], it was recognized that the discrete Pickands constant can be interpreted as an extremal index of a Brown–Resnick process. This new realization motivated the generalization of Pickands constants beyond the realm of Gaussian processes. For further references the reader may consult [Reference Dębicki, Engelke and Hashorva13, Reference Dębicki and Hashorva14], which give an excellent account of the history of Pickands constants, their connection to the theory of max-stable processes, and the most recent advances in the theory.
Although it is omnipresent in the asymptotic theory of stochastic processes, to date, the value of
![]() $\mathcal H_\alpha$
is known only in two very special cases:
$\mathcal H_\alpha$
is known only in two very special cases:
![]() $\alpha=1$
and
$\alpha=1$
and
![]() $\alpha=2$
. In these cases, the distribution of the supremum of process
$\alpha=2$
. In these cases, the distribution of the supremum of process
![]() $B_\alpha$
is well known:
$B_\alpha$
is well known:
![]() $B_1$
is a standard Brownian motion, while
$B_1$
is a standard Brownian motion, while
![]() $B_2$
is a straight line with random, normally distributed slope. When
$B_2$
is a straight line with random, normally distributed slope. When
![]() $\alpha\not\in\{1,2\}$
, one may attempt to estimate the numerical value of
$\alpha\not\in\{1,2\}$
, one may attempt to estimate the numerical value of
![]() $\mathcal H_\alpha$
from the definition (1) using Monte Carlo methods. However, there are several problems associated with this approach:
$\mathcal H_\alpha$
from the definition (1) using Monte Carlo methods. However, there are several problems associated with this approach:
-
(i) Firstly, the Pickands constant
 $\mathcal H_\alpha$
in (1) is defined as a limit as
$\mathcal H_\alpha$
in (1) is defined as a limit as
 $S\to\infty$
, so one must approximate it by choosing some (large) S. This results in a bias in the estimation, which we call the truncation error. The truncation error has been shown to decay faster than
$S\to\infty$
, so one must approximate it by choosing some (large) S. This results in a bias in the estimation, which we call the truncation error. The truncation error has been shown to decay faster than
 $S^{-p}$
for any
$S^{-p}$
for any
 $p<1$
; see [Reference Dębicki12, Corollary 3.1].
$p<1$
; see [Reference Dębicki12, Corollary 3.1]. -
(ii) Secondly, for every
 $\alpha\in(0,2)$
, the variance of the truncated estimator blows up as
$\alpha\in(0,2)$
, the variance of the truncated estimator blows up as
 $S\to\infty$
; that is, This can easily be seen by considering the second moment of
$S\to\infty$
; that is, This can easily be seen by considering the second moment of \[\lim_{S\to\infty}\textrm{var} \left\{\frac{1}{S}\text{sup}_{t\in [0,S]}\exp\{\sqrt 2 B_\alpha(t)-t^{\alpha}\}\right\} = \infty.\]
\[\lim_{S\to\infty}\textrm{var} \left\{\frac{1}{S}\text{sup}_{t\in [0,S]}\exp\{\sqrt 2 B_\alpha(t)-t^{\alpha}\}\right\} = \infty.\]
 $\tfrac{1}{S}\exp\{\sqrt{2}B_\alpha(S)-S^\alpha\}$
. This directly affects the sampling error (standard deviation) of the crude Monte Carlo estimator. As
$\tfrac{1}{S}\exp\{\sqrt{2}B_\alpha(S)-S^\alpha\}$
. This directly affects the sampling error (standard deviation) of the crude Monte Carlo estimator. As
 $S\to\infty$
, one needs more and more samples to prevent its variance from blowing up.
$S\to\infty$
, one needs more and more samples to prevent its variance from blowing up.
-
(iii) Finally, there are no methods available for the exact simulation of
 $\text{sup}_{t\in [0,S]}\exp\{\sqrt 2 B_\alpha(t)-t^{\alpha}\}$
for
$\text{sup}_{t\in [0,S]}\exp\{\sqrt 2 B_\alpha(t)-t^{\alpha}\}$
for
 $\alpha\not\in\{1,2\}$
. One must therefore resort to some method of approximation. Typically, one would simulate fBm on a regular
$\alpha\not\in\{1,2\}$
. One must therefore resort to some method of approximation. Typically, one would simulate fBm on a regular
 $\delta$
-grid, i.e. on the set
$\delta$
-grid, i.e. on the set
 $\delta\mathbb{Z}$
for
$\delta\mathbb{Z}$
for
 $\delta>0$
; cf. Equation (2) below. This approximation leads to a bias, which we call the discretization error.
$\delta>0$
; cf. Equation (2) below. This approximation leads to a bias, which we call the discretization error.
In the following, for any fixed
![]() $\delta>0$
we define the discrete Pickands constant
$\delta>0$
we define the discrete Pickands constant
where, for
![]() $a,b\in\mathbb{R}$
and
$a,b\in\mathbb{R}$
and
![]() $\delta>0$
,
$\delta>0$
,
![]() $[a,b]_\delta = [a,b]\cap \delta\mathbb{Z}$
. Additionally, we set
$[a,b]_\delta = [a,b]\cap \delta\mathbb{Z}$
. Additionally, we set
![]() $0\mathbb{Z} = \mathbb{R}$
, so that
$0\mathbb{Z} = \mathbb{R}$
, so that
![]() $\mathcal H^0_\alpha = \mathcal H_\alpha$
. In light of the discussion in item (iii) above, the discretization error equals
$\mathcal H^0_\alpha = \mathcal H_\alpha$
. In light of the discussion in item (iii) above, the discretization error equals
![]() $\mathcal H_\alpha-\mathcal H_\alpha^\delta$
. We should note that the quantity
$\mathcal H_\alpha-\mathcal H_\alpha^\delta$
. We should note that the quantity
![]() $\mathcal H_\alpha^\delta$
is well defined and
$\mathcal H_\alpha^\delta$
is well defined and
![]() $\mathcal{H}_{\alpha}^{\delta}\in (0,\infty)$
for
$\mathcal{H}_{\alpha}^{\delta}\in (0,\infty)$
for
![]() $\delta\ge0$
. Moreover,
$\delta\ge0$
. Moreover,
![]() $\mathcal{H}_{\alpha}^{\delta} \to \mathcal{H}_{\alpha}$
as
$\mathcal{H}_{\alpha}^{\delta} \to \mathcal{H}_{\alpha}$
as
![]() $\delta\to0$
, which means that the discretization error diminishes as the size of the gap of the grid goes to 0. We refer to [Reference Dębicki, Engelke and Hashorva13] for the proofs of these properties.
$\delta\to0$
, which means that the discretization error diminishes as the size of the gap of the grid goes to 0. We refer to [Reference Dębicki, Engelke and Hashorva13] for the proofs of these properties.
In recent years, [Reference Dieker and Yakir23] proposed a new representation of
![]() $\mathcal H^\delta_\alpha$
, which does not involve the limit operation. They show [Reference Dieker and Yakir23, Proposition 3] that for all
$\mathcal H^\delta_\alpha$
, which does not involve the limit operation. They show [Reference Dieker and Yakir23, Proposition 3] that for all
![]() $\delta\ge 0$
and
$\delta\ge 0$
and
![]() $\alpha\in(0,2]$
,
$\alpha\in(0,2]$
,
 \begin{eqnarray} \mathcal{H}_{\alpha}^\delta = \mathbb{E}\left\{ \xi_\alpha^\delta\right\}, \quad \textrm{where} \quad \xi_\alpha^\delta \;:\!=\; \frac{\text{sup}_{t\in\delta\mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in \delta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }}. \end{eqnarray}
\begin{eqnarray} \mathcal{H}_{\alpha}^\delta = \mathbb{E}\left\{ \xi_\alpha^\delta\right\}, \quad \textrm{where} \quad \xi_\alpha^\delta \;:\!=\; \frac{\text{sup}_{t\in\delta\mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in \delta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }}. \end{eqnarray}
For
![]() $\delta = 0$
the denominator in the fraction above is replaced by
$\delta = 0$
the denominator in the fraction above is replaced by
![]() $\int_{\mathbb{R}} e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}\textrm{d}t$
. In fact, the denominator can be replaced by
$\int_{\mathbb{R}} e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}\textrm{d}t$
. In fact, the denominator can be replaced by
![]() $\eta\sum_{t\in \eta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}$
for any
$\eta\sum_{t\in \eta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}$
for any
![]() $\eta$
, which is an integer multiple of
$\eta$
, which is an integer multiple of
![]() $\delta$
; see [Reference Dębicki, Engelke and Hashorva13, Theorem 2]. While one would ideally estimate
$\delta$
; see [Reference Dębicki, Engelke and Hashorva13, Theorem 2]. While one would ideally estimate
![]() $\mathcal H_\alpha$
using
$\mathcal H_\alpha$
using
![]() $\xi_\alpha^0$
, this is unfortunately infeasible since there are no exact simulation methods for
$\xi_\alpha^0$
, this is unfortunately infeasible since there are no exact simulation methods for
![]() $\xi^\delta_\alpha$
(see also item (iii) above). For that reason, the authors define the ‘truncated’ version of the random variable
$\xi^\delta_\alpha$
(see also item (iii) above). For that reason, the authors define the ‘truncated’ version of the random variable
![]() $\xi_\alpha^\delta$
, namely
$\xi_\alpha^\delta$
, namely
 \begin{align*}\xi_\alpha^\delta(T) \;:\!=\; \frac{\text{sup}_{t\in[\!-\!T,T]_\delta}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in[\!-\!T,T]_\delta}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }},\end{align*}
\begin{align*}\xi_\alpha^\delta(T) \;:\!=\; \frac{\text{sup}_{t\in[\!-\!T,T]_\delta}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in[\!-\!T,T]_\delta}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }},\end{align*}
where for
![]() $\delta = 0$
the denominator of the fraction is replaced by
$\delta = 0$
the denominator of the fraction is replaced by
![]() $\int_{-T}^T e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}\textrm{d}t$
. For any
$\int_{-T}^T e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}\textrm{d}t$
. For any
![]() $\delta,T\in(0,\infty)$
, the estimator
$\delta,T\in(0,\infty)$
, the estimator
![]() $\xi_\alpha^\delta(T)$
is a functional of a fractional Brownian motion on a finite grid, and as such it can be simulated exactly; see e.g. [Reference Dieker24] for a survey of methods of simulation of fBm. A side effect of this approach is that the new estimator induces both the truncation and the discretization errors described in items (i) and (iii) above.
$\xi_\alpha^\delta(T)$
is a functional of a fractional Brownian motion on a finite grid, and as such it can be simulated exactly; see e.g. [Reference Dieker24] for a survey of methods of simulation of fBm. A side effect of this approach is that the new estimator induces both the truncation and the discretization errors described in items (i) and (iii) above.
In this manuscript we rigorously show that the estimator
![]() $\xi_\alpha^\delta(T)$
is well suited for simulation. In Theorem 1, we address the conjecture stated by the inventors of the estimator
$\xi_\alpha^\delta(T)$
is well suited for simulation. In Theorem 1, we address the conjecture stated by the inventors of the estimator
![]() $\xi^\delta_\alpha$
about the asymptotic behavior of the discretization error between the continuous and discrete Pickands constant for a fixed
$\xi^\delta_\alpha$
about the asymptotic behavior of the discretization error between the continuous and discrete Pickands constant for a fixed
![]() $\alpha\in(0,2]$
:
$\alpha\in(0,2]$
:
[Reference Dieker and Yakir23, Conjecture 1] For all
![]() $\alpha\in(0,2]$
it holds that
$\alpha\in(0,2]$
it holds that
![]() $\displaystyle \lim_{\delta\to 0}\frac{\mathcal{H}_{\alpha}-\mathcal{H}_{\alpha}^{\delta}}{\delta^{\alpha/2}}\in (0,\infty).$
$\displaystyle \lim_{\delta\to 0}\frac{\mathcal{H}_{\alpha}-\mathcal{H}_{\alpha}^{\delta}}{\delta^{\alpha/2}}\in (0,\infty).$
We establish that the conjecture is true when
![]() $\alpha=1$
and is not true when
$\alpha=1$
and is not true when
![]() $\alpha=2$
; see Corollary 1 below, where the exact asymptotics of the discretization error are derived in these two special cases.
$\alpha=2$
; see Corollary 1 below, where the exact asymptotics of the discretization error are derived in these two special cases.
Furthermore, in Theorem 1(i) we show that
for
![]() $\alpha\in(0,1)$
, and in Theorem 1(ii) we show that
$\alpha\in(0,1)$
, and in Theorem 1(ii) we show that
![]() $\mathcal H_\alpha-\mathcal H_\alpha^\delta$
is upper-bounded by
$\mathcal H_\alpha-\mathcal H_\alpha^\delta$
is upper-bounded by
![]() $\delta^{\alpha/2}$
up to logarithmic terms for
$\delta^{\alpha/2}$
up to logarithmic terms for
![]() $\alpha\in(1,2)$
and all
$\alpha\in(1,2)$
and all
![]() $\delta>0$
small enough. These results support the claim of the conjecture for all
$\delta>0$
small enough. These results support the claim of the conjecture for all
![]() $\alpha\in(0,2)$
.
$\alpha\in(0,2)$
.
Secondly, we consider the truncation and sampling errors induced by
![]() $\xi_\alpha^\delta(T)$
. In Theorem 2 we derive a uniform upper bound for the tail of the probability distribution of
$\xi_\alpha^\delta(T)$
. In Theorem 2 we derive a uniform upper bound for the tail of the probability distribution of
![]() $\xi_\alpha^\delta$
which implies that all moments of
$\xi_\alpha^\delta$
which implies that all moments of
![]() $\xi_\alpha^\delta$
exist and are uniformly bounded in
$\xi_\alpha^\delta$
exist and are uniformly bounded in
![]() $\delta\in[0,1]$
. In Theorem 3 we establish that for any
$\delta\in[0,1]$
. In Theorem 3 we establish that for any
![]() $\alpha\in(0,2)$
and
$\alpha\in(0,2)$
and
![]() $p\ge1$
, the difference
$p\ge1$
, the difference
![]() $|\mathbb{E}(\xi_\alpha^\delta(T))^p - \mathbb{E}(\xi_\alpha^\delta)^p|$
decays no slower than
$|\mathbb{E}(\xi_\alpha^\delta(T))^p - \mathbb{E}(\xi_\alpha^\delta)^p|$
decays no slower than
![]() $\exp\{-\mathcal CT^\alpha\}$
, as
$\exp\{-\mathcal CT^\alpha\}$
, as
![]() $T\to\infty$
, uniformly for all
$T\to\infty$
, uniformly for all
![]() $\delta\in[0,1]$
. This implies that the truncation error of the Dieker–Yakir estimator decays no slower than
$\delta\in[0,1]$
. This implies that the truncation error of the Dieker–Yakir estimator decays no slower than
![]() $\exp\{-\mathcal CT^\alpha\}$
, and combining this with Theorem 2, we have that
$\exp\{-\mathcal CT^\alpha\}$
, and combining this with Theorem 2, we have that
![]() $\xi_\alpha^\delta(T)$
has a uniformly bounded sampling error, i.e.
$\xi_\alpha^\delta(T)$
has a uniformly bounded sampling error, i.e.
Although arguably the most celebrated, Pickands constants are not the only constants appearing in the asymptotic theory of Gaussian processes and related fields. Depending on the setting, other constants may appear, including Parisian Pickands constants [Reference Dębicki, Hashorva and Ji15, Reference Dębicki, Hashorva and Ji16, Reference Jasnovidov and Shemendyuk27], sojourn Pickands constants [Reference Dębicki, Liu and Michna18, Reference Dębicki, Michna and Peng20], Piterbarg-type constants [Reference Bai, Dębicki, Hashorva and Luo3, Reference Ji and Robert28, Reference Piterbarg33, Reference Piterbarg34], and generalized Pickands constants [Reference Dębicki11, Reference Dieker21]. As with the classical Pickands constants, the numerical values of these constants are typically known only in the case
![]() $\alpha\in\{1,2\}$
. To approximate them, one can try the discretization approach. We believe that, using techniques from the proof of Theorem 1(ii), one could derive upper bounds for the discretization error which are exact up to logarithmic terms; see, e.g., [Reference Bisewski and Jasnovidov6].
$\alpha\in\{1,2\}$
. To approximate them, one can try the discretization approach. We believe that, using techniques from the proof of Theorem 1(ii), one could derive upper bounds for the discretization error which are exact up to logarithmic terms; see, e.g., [Reference Bisewski and Jasnovidov6].
The manuscript is organized as follows. In Section 2 we present our main results and discuss their extensions and relationship to other problems. The rigorous proofs are presented in Section 3, while some technical calculations are given in the appendix.
2. Main results
In the following, we give an upper bound for
![]() $\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta}$
for all
$\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta}$
for all
![]() $\alpha\in(0,1)\cup(1,2)$
for small
$\alpha\in(0,1)\cup(1,2)$
for small
![]() $\delta>0$
.
$\delta>0$
.
Theorem 1. The following hold:
-
(i) For any
 $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
 $\varepsilon>0$
, for all
$\varepsilon>0$
, for all
 $\delta>0$
sufficiently small,
$\delta>0$
sufficiently small,  \begin{equation*}\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta} \leq \frac{\mathcal H_\alpha \sqrt{\pi}(1+\varepsilon)}{(1 - 2^{-1-\alpha/2})\sqrt{4-2^\alpha}} \cdot \delta^{\alpha/2}.\end{equation*}
\begin{equation*}\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta} \leq \frac{\mathcal H_\alpha \sqrt{\pi}(1+\varepsilon)}{(1 - 2^{-1-\alpha/2})\sqrt{4-2^\alpha}} \cdot \delta^{\alpha/2}.\end{equation*}
-
(ii) For every
 $\alpha\in(1,2)$
there exists
$\alpha\in(1,2)$
there exists
 $\mathcal C>0$
such that for all
$\mathcal C>0$
such that for all
 $\delta>0$
sufficiently small,
$\delta>0$
sufficiently small,  \begin{equation*}\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta} \leq\mathcal C\delta^{\alpha/2}|\log\delta|^{1/2}.\end{equation*}
\begin{equation*}\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta} \leq\mathcal C\delta^{\alpha/2}|\log\delta|^{1/2}.\end{equation*}
While for the proof of the case
![]() $\alpha\in(1,2)$
we were able to use general results from the theory of Gaussian processes, in the case
$\alpha\in(1,2)$
we were able to use general results from the theory of Gaussian processes, in the case
![]() $\alpha\in(0,1)$
we needed to come up with more precise tools in order to skip the
$\alpha\in(0,1)$
we needed to come up with more precise tools in order to skip the
![]() $|\log \delta|^{1/2}$
part in the upper bound. Therefore, the proofs in these two cases are very different from each other. Unfortunately, the proof in case (i) cannot be extended to case (ii) because of the switch from positive to negative correlations between the increments of fBm; see also Remark 1.
$|\log \delta|^{1/2}$
part in the upper bound. Therefore, the proofs in these two cases are very different from each other. Unfortunately, the proof in case (i) cannot be extended to case (ii) because of the switch from positive to negative correlations between the increments of fBm; see also Remark 1.
In the following two results we establish an upper bound for the survival function of
![]() $\xi_\alpha^\delta$
and for the truncation error discussed in item (i) in Section 1. These two results combined imply that the sampling error of
$\xi_\alpha^\delta$
and for the truncation error discussed in item (i) in Section 1. These two results combined imply that the sampling error of
![]() $\xi_\alpha^\delta(T)$
is uniformly bounded in
$\xi_\alpha^\delta(T)$
is uniformly bounded in
![]() $(\delta,T)\in[0,1]\times[1,\infty)$
; cf. Equation (4).
$(\delta,T)\in[0,1]\times[1,\infty)$
; cf. Equation (4).
Theorem 2. For any
![]() $\alpha \in (0,2)$
,
$\alpha \in (0,2)$
,
![]() $\delta\in[0,1]$
, and
$\delta\in[0,1]$
, and
![]() $\varepsilon>0$
for sufficiently large x, T, we have
$\varepsilon>0$
for sufficiently large x, T, we have
Moreover, there exist positive constants
![]() $\mathcal C_1, \mathcal C_2$
such that for all
$\mathcal C_1, \mathcal C_2$
such that for all
![]() $x,T>0$
and
$x,T>0$
and
![]() $\delta\ge 0$
,
$\delta\ge 0$
,
Evidently, Theorem 2 implies that all moments of
![]() $\xi_\alpha^\delta$
are finite and uniformly bounded in
$\xi_\alpha^\delta$
are finite and uniformly bounded in
![]() $\delta\in [0,1]$
for any fixed
$\delta\in [0,1]$
for any fixed
![]() $\alpha \in (0,2)$
.
$\alpha \in (0,2)$
.
Theorem 3. For any
![]() $\alpha\in (0,2)$
and
$\alpha\in (0,2)$
and
![]() $p>0$
there exist postive constants
$p>0$
there exist postive constants
![]() $\mathcal C_1,\mathcal C_2$
such that
$\mathcal C_1,\mathcal C_2$
such that
for all
![]() $(\delta,T)\in[0,1]\times[1,\infty)$
.
$(\delta,T)\in[0,1]\times[1,\infty)$
.
2.1. Case
 $\alpha\in\{1,2\}$
$\alpha\in\{1,2\}$
In this scenario, the explicit formulas for
![]() $\mathcal H_1^\delta$
(see, e.g., [Reference Dębicki and Mandjes19, Reference Kabluchko and Wang29]) and
$\mathcal H_1^\delta$
(see, e.g., [Reference Dębicki and Mandjes19, Reference Kabluchko and Wang29]) and
![]() $\mathcal H_2^\delta$
(see, e.g., [Reference Dębicki and Hashorva14, Equation (2.9)]) are known. They are summarized in the proposition below, with
$\mathcal H_2^\delta$
(see, e.g., [Reference Dębicki and Hashorva14, Equation (2.9)]) are known. They are summarized in the proposition below, with
![]() $\Phi$
being the cumulative distribution function of a standard Gaussian random variable.
$\Phi$
being the cumulative distribution function of a standard Gaussian random variable.
Proposition 1. It holds that
-
(i)
 $\mathcal H_1 = 1$
and
$\mathcal H_1 = 1$
and
 $\displaystyle \mathcal{H}^{\delta}_1 =\bigg(\delta\exp\Big\{2\sum_{k=1}^\infty\frac{\Phi(\!-\!\sqrt {\delta k/2})}{k}\Big\}\bigg)^{-1}$
for all
$\displaystyle \mathcal{H}^{\delta}_1 =\bigg(\delta\exp\Big\{2\sum_{k=1}^\infty\frac{\Phi(\!-\!\sqrt {\delta k/2})}{k}\Big\}\bigg)^{-1}$
for all
 $\delta>0$
, and
$\delta>0$
, and -
(ii)
 $\mathcal{H}_{2}=\frac{1}{\sqrt{\pi}}$
, and
$\mathcal{H}_{2}=\frac{1}{\sqrt{\pi}}$
, and
 $\displaystyle \mathcal{H}^\delta_{2}=\frac{2}{\delta}\left( \Phi(\delta/\sqrt{2})-\frac{1}{2} \right)$
for all
$\displaystyle \mathcal{H}^\delta_{2}=\frac{2}{\delta}\left( \Phi(\delta/\sqrt{2})-\frac{1}{2} \right)$
for all
 $\delta>0$
.
$\delta>0$
.
Relying on the above, we can provide the exact asymptotics of the discretization error, as
![]() $\delta\to0$
. In the following,
$\delta\to0$
. In the following,
![]() $\zeta$
denotes the Euler–Riemann zeta function.
$\zeta$
denotes the Euler–Riemann zeta function.
Corollary 1. It holds that
-
(i)
 $\displaystyle \lim_{\delta\to0}\frac{\mathcal H_1-\mathcal H_1^\delta}{\sqrt{\delta}} = -\frac{\zeta(1/2)}{\sqrt \pi}$
, and
$\displaystyle \lim_{\delta\to0}\frac{\mathcal H_1-\mathcal H_1^\delta}{\sqrt{\delta}} = -\frac{\zeta(1/2)}{\sqrt \pi}$
, and -
(ii)
 $\displaystyle \lim_{\delta\to0}\frac{\mathcal H_2-\mathcal H_2^\delta}{\delta^2} = \frac{1}{12\sqrt{\pi}}$
.
$\displaystyle \lim_{\delta\to0}\frac{\mathcal H_2-\mathcal H_2^\delta}{\delta^2} = \frac{1}{12\sqrt{\pi}}$
.
2.2. Discussion
We believe that finding the exact asymptotics of the speed of the discretization error
![]() $\mathcal H_{\alpha}-\mathcal H_\alpha^\delta$
is closely related to the behavior of fBm around the time of its supremum. We motivate this by the following heuristic:
$\mathcal H_{\alpha}-\mathcal H_\alpha^\delta$
is closely related to the behavior of fBm around the time of its supremum. We motivate this by the following heuristic:
 \begin{align*}\mathcal H_\alpha - \mathcal H_\alpha^\delta &= \mathbb{E}\left\{ \frac{\text{sup}_{t\in\mathbb{R}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}} - \text{sup}_{t\in\delta\mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in \delta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }}\right\} \\[5pt] & \approx \mathbb{E}\left\{ \Delta(\delta) \cdot \frac{\text{sup}_{t\in\delta\mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in \delta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }}\right\}, \\[5pt] & \approx \mathbb{E}\left\{ \Delta(\delta)\right\}\cdot \mathcal H^\delta_\alpha,\end{align*}
\begin{align*}\mathcal H_\alpha - \mathcal H_\alpha^\delta &= \mathbb{E}\left\{ \frac{\text{sup}_{t\in\mathbb{R}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}} - \text{sup}_{t\in\delta\mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in \delta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }}\right\} \\[5pt] & \approx \mathbb{E}\left\{ \Delta(\delta) \cdot \frac{\text{sup}_{t\in\delta\mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha}}}{\delta\sum_{t\in \delta \mathbb{Z}}e^{\sqrt 2B_\alpha(t)-|t|^{\alpha} }}\right\}, \\[5pt] & \approx \mathbb{E}\left\{ \Delta(\delta)\right\}\cdot \mathcal H^\delta_\alpha,\end{align*}
where
![]() $\Delta(\delta)$
is the difference between the suprema on the continuous and discrete grids, i.e.
$\Delta(\delta)$
is the difference between the suprema on the continuous and discrete grids, i.e.
![]() $\Delta(\delta) \;:\!=\; \text{sup}_{t\in\mathbb{R}}\{\sqrt{2}B_\alpha(t)-|t|^{\alpha}\} - \text{sup}_{t\in\delta\mathbb{Z}}\{\sqrt{2}B_\alpha(t)-|t|^{\alpha}\}$
. The first approximation above is due to the mean value theorem, and the second approximation is based on the assumption that
$\Delta(\delta) \;:\!=\; \text{sup}_{t\in\mathbb{R}}\{\sqrt{2}B_\alpha(t)-|t|^{\alpha}\} - \text{sup}_{t\in\delta\mathbb{Z}}\{\sqrt{2}B_\alpha(t)-|t|^{\alpha}\}$
. The first approximation above is due to the mean value theorem, and the second approximation is based on the assumption that
![]() $\Delta(\delta)$
and
$\Delta(\delta)$
and
![]() $\xi^\delta_\alpha$
are asymptotically independent as
$\xi^\delta_\alpha$
are asymptotically independent as
![]() $\delta\to0$
. We believe that
$\delta\to0$
. We believe that
![]() $\Delta(\delta)\sim \mathcal C\delta^{\alpha/2}$
by self-similarity, where
$\Delta(\delta)\sim \mathcal C\delta^{\alpha/2}$
by self-similarity, where
![]() $\mathcal C>0$
is some constant, which would imply that
$\mathcal C>0$
is some constant, which would imply that
![]() $\mathcal H_\alpha-\mathcal H_\alpha^\delta \sim \mathcal C\mathcal H_\alpha\delta^{\alpha/2}$
. This heuristic reasoning can be made rigorous in the case
$\mathcal H_\alpha-\mathcal H_\alpha^\delta \sim \mathcal C\mathcal H_\alpha\delta^{\alpha/2}$
. This heuristic reasoning can be made rigorous in the case
![]() $\alpha=1$
, when
$\alpha=1$
, when
![]() $\sqrt{2}B_\alpha(t)-|t|^\alpha$
is a Lévy process (Brownian motion with drift). In this case, the asymptotic behavior of functionals such as
$\sqrt{2}B_\alpha(t)-|t|^\alpha$
is a Lévy process (Brownian motion with drift). In this case, the asymptotic behavior of functionals such as
![]() $\mathbb{E}\left\{ \Delta(\delta)\right\}$
, as
$\mathbb{E}\left\{ \Delta(\delta)\right\}$
, as
![]() $\delta\to0$
, can be explained by the weak convergence of trajectories around the time of supremum to the so-called Lévy process conditioned to be positive; see [Reference Ivanovs26] for more information on this topic. In fact, Corollary 1(i) can be proven using the tools developed in [Reference Bisewski and Ivanovs5]. To the best of the authors’ knowledge, there are no such results available for a general fBm. However, it is worth mentioning that recently [Reference Aurzada, Buck and Kilian2] considered the related problem of penalizing fractional Brownian motion for being negative.
$\delta\to0$
, can be explained by the weak convergence of trajectories around the time of supremum to the so-called Lévy process conditioned to be positive; see [Reference Ivanovs26] for more information on this topic. In fact, Corollary 1(i) can be proven using the tools developed in [Reference Bisewski and Ivanovs5]. To the best of the authors’ knowledge, there are no such results available for a general fBm. However, it is worth mentioning that recently [Reference Aurzada, Buck and Kilian2] considered the related problem of penalizing fractional Brownian motion for being negative.
A problem related to the asymptotic behavior of
![]() $\mathcal H_\alpha- \mathcal H_\alpha^\delta$
was considered in [Reference Borovkov, Mishura, Novikov and Zhitlukhin7, Reference Borovkov, Mishura, Novikov and Zhitlukhin8], who showed that
$\mathcal H_\alpha- \mathcal H_\alpha^\delta$
was considered in [Reference Borovkov, Mishura, Novikov and Zhitlukhin7, Reference Borovkov, Mishura, Novikov and Zhitlukhin8], who showed that
![]() $\mathbb{E} \text{sup}_{t\in [0,1]}B_\alpha(t)-\mathbb{E} \text{sup}_{t\in [0,1]_\delta}B_\alpha(t)$
decays like
$\mathbb{E} \text{sup}_{t\in [0,1]}B_\alpha(t)-\mathbb{E} \text{sup}_{t\in [0,1]_\delta}B_\alpha(t)$
decays like
![]() $\delta^{\alpha/2}$
up to logarithmic terms. We should emphasize that in Theorem 1, in the case
$\delta^{\alpha/2}$
up to logarithmic terms. We should emphasize that in Theorem 1, in the case
![]() $\alpha\in(0,1)$
, we were able to establish that the upper bound for the discretization error decays exactly like
$\alpha\in(0,1)$
, we were able to establish that the upper bound for the discretization error decays exactly like
![]() $\delta^{\alpha/2}$
. In light of the discussion above, we believe that the result and the method of proof of Theorem 1(i) could be useful in further research related to the discretization error for fBm.
$\delta^{\alpha/2}$
. In light of the discussion above, we believe that the result and the method of proof of Theorem 1(i) could be useful in further research related to the discretization error for fBm.
Monotonicity of Pickands constants. Based on the definition (2), it is clear that for any
![]() $\alpha\in(0,2)$
, the sequence
$\alpha\in(0,2)$
, the sequence
![]() $\{\mathcal H^{\delta}_\alpha, \mathcal H^{2\delta}_\alpha,\mathcal H^{4\delta}_\alpha, \ldots\}$
is decreasing for any fixed
$\{\mathcal H^{\delta}_\alpha, \mathcal H^{2\delta}_\alpha,\mathcal H^{4\delta}_\alpha, \ldots\}$
is decreasing for any fixed
![]() $\delta>0$
. It is therefore natural to speculate that
$\delta>0$
. It is therefore natural to speculate that
![]() $\delta\mapsto\mathcal H_\alpha^\delta$
is a decreasing function. The explicit formulas for
$\delta\mapsto\mathcal H_\alpha^\delta$
is a decreasing function. The explicit formulas for
![]() $\mathcal H_1^\delta$
and
$\mathcal H_1^\delta$
and
![]() $\mathcal H_2^\delta$
given in Proposition 1 allow us to give a positive answer to this question in these cases.
$\mathcal H_2^\delta$
given in Proposition 1 allow us to give a positive answer to this question in these cases.
Corollary 2. For all
![]() $\delta\ge 0$
,
$\delta\ge 0$
,
![]() $\mathcal{H}^{\delta}_1$
and
$\mathcal{H}^{\delta}_1$
and
![]() $\mathcal{H}^{\delta}_2$
are strictly decreasing functions with respect to
$\mathcal{H}^{\delta}_2$
are strictly decreasing functions with respect to
![]() $\delta$
.
$\delta$
.
3. Proofs
For
![]() $\alpha \in (0,2)$
define
$\alpha \in (0,2)$
define
Assume that all of the random processes and variables we consider are defined on a complete general probability space
![]() $\Omega$
equipped with a probability measure
$\Omega$
equipped with a probability measure
![]() $\mathbb P$
. Let
$\mathbb P$
. Let
![]() $\mathcal C,\mathcal C_1,\mathcal C_2,\ldots$
be some positive constants that may differ from line to line.
$\mathcal C,\mathcal C_1,\mathcal C_2,\ldots$
be some positive constants that may differ from line to line.
3.1. Proof of Theorem 1, case
 $\alpha\in(0,1)$
$\alpha\in(0,1)$
The proof of Theorem 1 in the case
![]() $\alpha\in(0,1)$
is based on the following three results, whose proofs are given later in this section. In what follows,
$\alpha\in(0,1)$
is based on the following three results, whose proofs are given later in this section. In what follows,
![]() $\eta$
is independent of
$\eta$
is independent of
![]() $\{Z_\alpha(t), t\in\mathbb{R}\}$
and follows a standard exponential distribution.
$\{Z_\alpha(t), t\in\mathbb{R}\}$
and follows a standard exponential distribution.
Lemma 1. For all
![]() $\alpha\in (0,2)$
,
$\alpha\in (0,2)$
,
As a side note, we remark that the representation in Lemma 1 yields a straightforward lower bound
for all
![]() $\alpha\in(0,2)$
,
$\alpha\in(0,2)$
,
![]() $\delta>0$
.
$\delta>0$
.
Lemma 2. For all
![]() $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
![]() $\delta>0$
,
$\delta>0$
,
Proposition 2. For any
![]() $\alpha\in(0,2)$
and
$\alpha\in(0,2)$
and
![]() $\varepsilon>0$
, it holds that
$\varepsilon>0$
, it holds that
for all
![]() $\delta>0$
small enough.
$\delta>0$
small enough.
Proof of Theorem
1,
![]() $\alpha\in (0,1)$
. Using the fact that
$\alpha\in (0,1)$
. Using the fact that
![]() $\mathcal H^\delta_\alpha \to \mathcal H_\alpha$
as
$\mathcal H^\delta_\alpha \to \mathcal H_\alpha$
as
![]() $\delta\downarrow0$
, we may represent the discretization error
$\delta\downarrow0$
, we may represent the discretization error
![]() $\mathcal H_\alpha - \mathcal H^\delta_\alpha$
as a telescoping series; that is,
$\mathcal H_\alpha - \mathcal H^\delta_\alpha$
as a telescoping series; that is,
Combining Lemma 2 and Proposition 2, we find that, with
![]() $\mathcal C$
denoting the constant from Proposition 2,
$\mathcal C$
denoting the constant from Proposition 2,
for all
![]() $\delta$
small enough. This completes the proof.
$\delta$
small enough. This completes the proof.
Remark 1. If the upper bound in Lemma 2 holds also for
![]() $\alpha\in(1,2)$
, then the upper bound in Theorem 1(i) holds for all
$\alpha\in(1,2)$
, then the upper bound in Theorem 1(i) holds for all
![]() $\alpha\in(0,2)$
.
$\alpha\in(0,2)$
.
The remainder of this section is devoted to proving Lemma 1, Lemma 2, and Proposition 2.
In what follows, for any
![]() $\alpha\in(0,2)$
, let
$\alpha\in(0,2)$
, let
![]() $\{X_\alpha(t), t\in\mathbb{R}\}$
be a centered, stationary Gaussian process with
$\{X_\alpha(t), t\in\mathbb{R}\}$
be a centered, stationary Gaussian process with
![]() $\textrm{var}\{X_\alpha(t)\} = 1$
, whose covariance function satisfies
$\textrm{var}\{X_\alpha(t)\} = 1$
, whose covariance function satisfies
Before we give the proof of Lemma 1, we introduce the following result.
Lemma 3. The finite-dimensional distributions of
![]() $\{u(X_\alpha(u^{-2/\alpha}t)-u) \mid X_\alpha(0)>u, t\in\mathbb{R}\}$
converge weakly to the finite-dimensional distributions of
$\{u(X_\alpha(u^{-2/\alpha}t)-u) \mid X_\alpha(0)>u, t\in\mathbb{R}\}$
converge weakly to the finite-dimensional distributions of
![]() $\{Z_\alpha(t)+\eta, t\in\mathbb{R}\}$
, where
$\{Z_\alpha(t)+\eta, t\in\mathbb{R}\}$
, where
![]() $\eta$
is a random variable independent of
$\eta$
is a random variable independent of
![]() $\{Z_\alpha(t), t\in\mathbb{R}\}$
following a standard exponential distribution.
$\{Z_\alpha(t), t\in\mathbb{R}\}$
following a standard exponential distribution.
The result in Lemma 3 is well known; see, e.g., [Reference Albin and Choi1, Lemma 2], where the convergence of finite-dimensional distributions is established on
![]() $t\in\mathbb{R}_+$
. The extension to
$t\in\mathbb{R}_+$
. The extension to
![]() $t\in\mathbb{R}$
is straightforward.
$t\in\mathbb{R}$
is straightforward.
Proof of Lemma
1. The following proof is very similar in flavor to the proof of [Reference Bisewski, Hashorva and Shevchenko4, Lemma 3.1]. From [Reference Piterbarg34, Lemma 9.2.2] and the classical definition of the Pickands constant it follows that for any
![]() $\alpha\in (0,2)$
and
$\alpha\in (0,2)$
and
![]() $\delta\ge 0$
,
$\delta\ge 0$
,
where
![]() $\Psi(u)$
is the complementary CDF (tail) of the standard normal distribution and
$\Psi(u)$
is the complementary CDF (tail) of the standard normal distribution and
![]() $\{X_\alpha, t\in\mathbb{R}\}$
is the process introduced above Equation (5). Therefore,
$\{X_\alpha, t\in\mathbb{R}\}$
is the process introduced above Equation (5). Therefore,
Now, notice that we can decompose the event in the numerator above into a sum of disjoint events:
 \begin{align*}& \frac{1}{\Psi(u)}\mathbb{P} \left\{ \displaystyle\max_{t\in[0,T]_{\delta/2}}X_\alpha(u^{-2/\alpha}t) > u, \max_{t\in[0,T]_\delta} X_\alpha(u^{-2/\alpha}t) < u \right \} \\[5pt] & = \sum_{\tau\in[0,T]_{\delta/2}}\mathbb{P} \left\{ \max_{t\in [0,T]_{\delta/2}} X_\alpha(u^{-2/\alpha}t) \leq X_\alpha(u^{-2/\alpha}\tau), \max_{t\in[0,T]_{\delta}} X_\alpha(u^{-2/\alpha}t) \leq u \mid X_\alpha(u^{-2/\alpha}\tau) > u \right \} .\end{align*}
\begin{align*}& \frac{1}{\Psi(u)}\mathbb{P} \left\{ \displaystyle\max_{t\in[0,T]_{\delta/2}}X_\alpha(u^{-2/\alpha}t) > u, \max_{t\in[0,T]_\delta} X_\alpha(u^{-2/\alpha}t) < u \right \} \\[5pt] & = \sum_{\tau\in[0,T]_{\delta/2}}\mathbb{P} \left\{ \max_{t\in [0,T]_{\delta/2}} X_\alpha(u^{-2/\alpha}t) \leq X_\alpha(u^{-2/\alpha}\tau), \max_{t\in[0,T]_{\delta}} X_\alpha(u^{-2/\alpha}t) \leq u \mid X_\alpha(u^{-2/\alpha}\tau) > u \right \} .\end{align*}
Using the stationarity of the process
![]() $X_\alpha$
, the above is equal to
$X_\alpha$
, the above is equal to
Applying Lemma 3 to each element of the sum above, we find that the sum converges to
![]() $\sum_{\tau\in[0,T]_{\delta/2}} U(\tau,T)$
as
$\sum_{\tau\in[0,T]_{\delta/2}} U(\tau,T)$
as
![]() $u\to\infty$
, where
$u\to\infty$
, where
We have now established that
![]() $\mathcal H_\alpha^{\delta/2}-\mathcal H_\alpha^\delta = \lim_{T\to\infty}\frac{1}{T}\sum_{\tau\in[0,T]_{\delta/2}}U(\tau,T)$
. Clearly,
$\mathcal H_\alpha^{\delta/2}-\mathcal H_\alpha^\delta = \lim_{T\to\infty}\frac{1}{T}\sum_{\tau\in[0,T]_{\delta/2}}U(\tau,T)$
. Clearly,
We will now show that
![]() $\mathcal H_\alpha^{\delta/2}-\mathcal H_\alpha^{\delta}$
is lower-bounded and upper-bounded by
$\mathcal H_\alpha^{\delta/2}-\mathcal H_\alpha^{\delta}$
is lower-bounded and upper-bounded by
![]() $\delta^{-1}U(0,\infty)$
, which will complete the proof. For the lower bound note that
$\delta^{-1}U(0,\infty)$
, which will complete the proof. For the lower bound note that
where the limit is equal to
![]() $\delta^{-1}U(0,\infty)$
, because the sum above has
$\delta^{-1}U(0,\infty)$
, because the sum above has
![]() $[T(\delta/2)^{-1}]$
elements, of which half are equal to 0 and the other half are equal to
$[T(\delta/2)^{-1}]$
elements, of which half are equal to 0 and the other half are equal to
![]() $U(0,\infty)$
. In order to show the upper bound, consider
$U(0,\infty)$
. In order to show the upper bound, consider
![]() $\varepsilon>0$
. For any
$\varepsilon>0$
. For any
![]() $\tau\in(\varepsilon T,(1-\varepsilon)T)_{\delta/2}$
we have
$\tau\in(\varepsilon T,(1-\varepsilon)T)_{\delta/2}$
we have
Furthermore, we have the following decomposition:
 \begin{align*}\mathcal H_\alpha^{\delta/2}-\mathcal H_\alpha^\delta & = \lim_{T\to\infty}\frac{1}{T}\left(\sum_{\tau\in(\delta/2)\mathbb{Z}\cap I_-} U(\tau,T) + \sum_{\tau\in(\delta/2)\mathbb{Z} \cap I_0} U(\tau,T) + \sum_{\tau\in(\delta/2)\mathbb{Z}\cap I_+} U(\tau,T)\right),\end{align*}
\begin{align*}\mathcal H_\alpha^{\delta/2}-\mathcal H_\alpha^\delta & = \lim_{T\to\infty}\frac{1}{T}\left(\sum_{\tau\in(\delta/2)\mathbb{Z}\cap I_-} U(\tau,T) + \sum_{\tau\in(\delta/2)\mathbb{Z} \cap I_0} U(\tau,T) + \sum_{\tau\in(\delta/2)\mathbb{Z}\cap I_+} U(\tau,T)\right),\end{align*}
where
![]() $I_- \;:\!=\; [0,\varepsilon T]$
,
$I_- \;:\!=\; [0,\varepsilon T]$
,
![]() $I_0 \;:\!=\; (\varepsilon T,(1-\varepsilon)T)$
,
$I_0 \;:\!=\; (\varepsilon T,(1-\varepsilon)T)$
,
![]() $I_+ \;:\!=\; [(1-\varepsilon),T]$
. The first and last sums can be bounded by their number of elements,
$I_+ \;:\!=\; [(1-\varepsilon),T]$
. The first and last sums can be bounded by their number of elements,
![]() $[\varepsilon T(\delta/2)^{-1}]$
, because
$[\varepsilon T(\delta/2)^{-1}]$
, because
![]() $U(\tau,T)\leq 1$
. The middle sum can be bounded by
$U(\tau,T)\leq 1$
. The middle sum can be bounded by
![]() $\frac{1}{2}\cdot [(1-2\varepsilon)T(\delta/2)^{-1}]\overline U(T,\varepsilon)$
, because half of its elements are equal to 0 and the other half can be upper-bounded by
$\frac{1}{2}\cdot [(1-2\varepsilon)T(\delta/2)^{-1}]\overline U(T,\varepsilon)$
, because half of its elements are equal to 0 and the other half can be upper-bounded by
![]() $\overline U(T,\varepsilon)$
. Letting
$\overline U(T,\varepsilon)$
. Letting
![]() $T\to\infty$
, we obtain
$T\to\infty$
, we obtain
because
![]() $\overline U(T,\varepsilon) \to U(0,\infty)$
as
$\overline U(T,\varepsilon) \to U(0,\infty)$
as
![]() $T\to\infty$
. Finally, letting
$T\to\infty$
. Finally, letting
![]() $\varepsilon\to0$
yields the desired result.
$\varepsilon\to0$
yields the desired result.
Proof of Lemma 2. In light of Lemma 1, it suffices to show that
The left-hand side of the above equals
 \begin{align*}& \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right) - |t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^\alpha + \eta < 0 \right \} \\[5pt] & \qquad = \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} - |t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2} + \frac{\eta}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} < 0 \right \} \\[5pt] & \qquad \leq \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} - |t|^{\alpha/2} + \frac{\eta}{|t|^{\alpha/2}} < 0 \right \} .\end{align*}
\begin{align*}& \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right) - |t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^\alpha + \eta < 0 \right \} \\[5pt] & \qquad = \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} - |t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2} + \frac{\eta}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} < 0 \right \} \\[5pt] & \qquad \leq \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} - |t|^{\alpha/2} + \frac{\eta}{|t|^{\alpha/2}} < 0 \right \} .\end{align*}
Observe that for all
![]() $t,s\in\delta\mathbb{Z}\setminus\{0\}$
it holds that
$t,s\in\delta\mathbb{Z}\setminus\{0\}$
it holds that
 \begin{equation}\textrm{cov}\!\left(\frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}}, \frac{\sqrt{2}B_\alpha(s - \tfrac{\delta}{2}\cdot\textrm{sgn}(s))}{|s - \tfrac{\delta}{2}\cdot\textrm{sgn}(s)|^{\alpha/2}} \right) \leq \textrm{cov}\left(\frac{\sqrt{2}B_\alpha(t)}{|t|^{\alpha/2}}, \frac{\sqrt{2}B_\alpha(s)}{|s|^{\alpha/2}}\right);\end{equation}
\begin{equation}\textrm{cov}\!\left(\frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}}, \frac{\sqrt{2}B_\alpha(s - \tfrac{\delta}{2}\cdot\textrm{sgn}(s))}{|s - \tfrac{\delta}{2}\cdot\textrm{sgn}(s)|^{\alpha/2}} \right) \leq \textrm{cov}\left(\frac{\sqrt{2}B_\alpha(t)}{|t|^{\alpha/2}}, \frac{\sqrt{2}B_\alpha(s)}{|s|^{\alpha/2}}\right);\end{equation}
the proof of this technical inequality is given in the appendix. Since in the case
![]() $t=s$
the covariances in Equation (6) are equal, we may apply the Slepian lemma [Reference Piterbarg34, Lemma 2.1.1] and obtain
$t=s$
the covariances in Equation (6) are equal, we may apply the Slepian lemma [Reference Piterbarg34, Lemma 2.1.1] and obtain
 \begin{align*}\mathbb{P} & \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} - |t|^{\alpha/2} + \frac{\eta}{|t|^{\alpha/2}} < 0 \right \}\\[5pt] & \leq \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha(t)}{|t|^{\alpha/2}} - |t|^{\alpha/2} + \frac{\eta}{|t|^{\alpha/2}} < 0 \right \},\end{align*}
\begin{align*}\mathbb{P} & \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha\!\left(t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)\right)}{|t - \tfrac{\delta}{2}\cdot\textrm{sgn}(t)|^{\alpha/2}} - |t|^{\alpha/2} + \frac{\eta}{|t|^{\alpha/2}} < 0 \right \}\\[5pt] & \leq \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} \frac{\sqrt{2}B_\alpha(t)}{|t|^{\alpha/2}} - |t|^{\alpha/2} + \frac{\eta}{|t|^{\alpha/2}} < 0 \right \},\end{align*}
from which the claim follows.
We will now lay out the preliminaries necessary to prove Proposition 2. First, let us introduce some notation that will be used until the end of this section. For any
![]() $\delta>0$
,
$\delta>0$
,
![]() $\lambda>0$
let
$\lambda>0$
let
 \begin{equation}\begin{split}& p(\delta) \;:\!=\; \mathbb{P} \left\{ A(\delta) \right \} , \quad \textrm{ with } \quad A(\delta) \;:\!=\; \{Z_\alpha(\!-\!\delta) < 0,Z_\alpha(\delta) < 0\}, \textrm{ and} \\[5pt] & q(\delta, \lambda) \;:\!=\; \mathbb{P} \left\{ A(\delta,\lambda) \right \} , \quad \textrm{ with } \quad A(\delta,\lambda) \;:\!=\; \{Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta < 0,Z_\alpha(\delta) + \lambda^{-1}\eta < 0\}.\end{split}\end{equation}
\begin{equation}\begin{split}& p(\delta) \;:\!=\; \mathbb{P} \left\{ A(\delta) \right \} , \quad \textrm{ with } \quad A(\delta) \;:\!=\; \{Z_\alpha(\!-\!\delta) < 0,Z_\alpha(\delta) < 0\}, \textrm{ and} \\[5pt] & q(\delta, \lambda) \;:\!=\; \mathbb{P} \left\{ A(\delta,\lambda) \right \} , \quad \textrm{ with } \quad A(\delta,\lambda) \;:\!=\; \{Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta < 0,Z_\alpha(\delta) + \lambda^{-1}\eta < 0\}.\end{split}\end{equation}
For any
![]() $\delta>0$
and
$\delta>0$
and
![]() $\lambda>0$
we define the densities of the two-dimensional vectors
$\lambda>0$
we define the densities of the two-dimensional vectors
![]() $(Z_\alpha(\!-\!\delta), Z_\alpha(\delta))$
and
$(Z_\alpha(\!-\!\delta), Z_\alpha(\delta))$
and
![]() $(Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta, Z_\alpha(\delta)+ \lambda^{-1}\eta)$
respectively, with
$(Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta, Z_\alpha(\delta)+ \lambda^{-1}\eta)$
respectively, with
![]() $\textbf{x} \;:\!=\; \left(\begin{smallmatrix} x_1\\[5pt] x_2 \end{smallmatrix}\right) \in\mathbb{R}^2$
, as follows:
$\textbf{x} \;:\!=\; \left(\begin{smallmatrix} x_1\\[5pt] x_2 \end{smallmatrix}\right) \in\mathbb{R}^2$
, as follows:
 \begin{align}\begin{split}f(\textbf{x};\; \delta) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta)\in\textrm{d}x_1,Z_\alpha(\delta)\in\textrm{d}x_2 \right \} }{\textrm{d}x_1\textrm{d}x_2}, \\[5pt] g(\textbf{x};\; \delta, \lambda) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta \in\textrm{d}x_1, Z_\alpha(\delta) + \lambda^{-1}\eta \in\textrm{d}x_2 \right \} }{\textrm{d}x_1\textrm{d}x_2}.\end{split}\end{align}
\begin{align}\begin{split}f(\textbf{x};\; \delta) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta)\in\textrm{d}x_1,Z_\alpha(\delta)\in\textrm{d}x_2 \right \} }{\textrm{d}x_1\textrm{d}x_2}, \\[5pt] g(\textbf{x};\; \delta, \lambda) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta \in\textrm{d}x_1, Z_\alpha(\delta) + \lambda^{-1}\eta \in\textrm{d}x_2 \right \} }{\textrm{d}x_1\textrm{d}x_2}.\end{split}\end{align}
We also define the densities of these random vectors conditioned to take negative values on both coordinates:
 \begin{align}\begin{split}f^-(\textbf{x};\; \delta) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta) \in\textrm{d}x_1, Z_\alpha(\delta) \in\textrm{d}x_2 \mid A(\delta) \right \} }{\textrm{d}x_1\textrm{d}x_2},\\[5pt] g^-(\textbf{x};\; \delta, \lambda) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta \in\textrm{d}x_1, Z_\alpha(\delta) + \lambda^{-1}\eta \in\textrm{d}x_2 \mid A(\delta,\lambda) \right \} }{\textrm{d}x_1\textrm{d}x_2}.\end{split}\end{align}
\begin{align}\begin{split}f^-(\textbf{x};\; \delta) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta) \in\textrm{d}x_1, Z_\alpha(\delta) \in\textrm{d}x_2 \mid A(\delta) \right \} }{\textrm{d}x_1\textrm{d}x_2},\\[5pt] g^-(\textbf{x};\; \delta, \lambda) & \;:\!=\; \frac{\mathbb{P} \left\{ Z_\alpha(\!-\!\delta) + \lambda^{-1}\eta \in\textrm{d}x_1, Z_\alpha(\delta) + \lambda^{-1}\eta \in\textrm{d}x_2 \mid A(\delta,\lambda) \right \} }{\textrm{d}x_1\textrm{d}x_2}.\end{split}\end{align}
Notice that both
![]() $f^-$
and
$f^-$
and
![]() $g^-$
are nonzero in the same domain
$g^-$
are nonzero in the same domain
![]() $\textbf{x}\leq \textbf{0}$
. Now, let
$\textbf{x}\leq \textbf{0}$
. Now, let
![]() $\Sigma$
be the covariance matrix of
$\Sigma$
be the covariance matrix of
![]() $(Z_\alpha(\!-\!1), Z_\alpha(1))$
, that is,
$(Z_\alpha(\!-\!1), Z_\alpha(1))$
, that is,
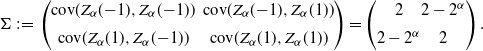 \begin{equation}\Sigma \;:\!=\; \begin{pmatrix}\textrm{cov}(Z_\alpha(\!-\!1), Z_\alpha(\!-\!1)) \ & \ \textrm{cov}(Z_\alpha(\!-\!1), Z_\alpha(1)) \\[5pt] \textrm{cov}(Z_\alpha(1), Z_\alpha(\!-\!1)) \ & \ \textrm{cov}(Z_\alpha(1), Z_\alpha(1))\end{pmatrix}= \begin{pmatrix}2 & 2-2^\alpha \\[5pt] 2-2^\alpha & 2\end{pmatrix}.\end{equation}
\begin{equation}\Sigma \;:\!=\; \begin{pmatrix}\textrm{cov}(Z_\alpha(\!-\!1), Z_\alpha(\!-\!1)) \ & \ \textrm{cov}(Z_\alpha(\!-\!1), Z_\alpha(1)) \\[5pt] \textrm{cov}(Z_\alpha(1), Z_\alpha(\!-\!1)) \ & \ \textrm{cov}(Z_\alpha(1), Z_\alpha(1))\end{pmatrix}= \begin{pmatrix}2 & 2-2^\alpha \\[5pt] 2-2^\alpha & 2\end{pmatrix}.\end{equation}
By the self-similarity property of fBm, the covariance matrix
![]() $\Sigma(\delta)$
of
$\Sigma(\delta)$
of
![]() $(Z_\alpha(\!-\!\delta), Z_\alpha(\delta))$
equals
$(Z_\alpha(\!-\!\delta), Z_\alpha(\delta))$
equals
![]() $\Sigma(\delta) = \delta^{\alpha}\Sigma$
. With
$\Sigma(\delta) = \delta^{\alpha}\Sigma$
. With
![]() ${\textbf{1}}_2 = \left(\begin{array}{c}{1} \\[2pt] {1}\end{array}\right)$
we define
${\textbf{1}}_2 = \left(\begin{array}{c}{1} \\[2pt] {1}\end{array}\right)$
we define
so that, with
![]() $|\Sigma|$
denoting the determinant of matrix
$|\Sigma|$
denoting the determinant of matrix
![]() $\Sigma$
, we have
$\Sigma$
, we have
 \begin{align*}f(\textbf{x};\; \delta) & = \frac{1}{2\pi|\Sigma|^{1/2}\delta^{\alpha}} \exp\!\left\{-\frac{(\textbf{x}+{\mathbf{1}}_2\delta^\alpha)^\top\Sigma(\delta)^{-1}(\textbf{x}+{ \mathbf{1}}_2\delta^\alpha)}{2\delta^{\alpha}}\right\}\\[5pt] & = \frac{1}{2\pi|\Sigma|^{1/2}\delta^{\alpha}} \exp\!\left\{-\frac{a(\textbf{x}) + 2b(\textbf{x})\delta^{\alpha} + c\delta^{2\alpha}}{2\delta^{\alpha}}\right\}.\end{align*}
\begin{align*}f(\textbf{x};\; \delta) & = \frac{1}{2\pi|\Sigma|^{1/2}\delta^{\alpha}} \exp\!\left\{-\frac{(\textbf{x}+{\mathbf{1}}_2\delta^\alpha)^\top\Sigma(\delta)^{-1}(\textbf{x}+{ \mathbf{1}}_2\delta^\alpha)}{2\delta^{\alpha}}\right\}\\[5pt] & = \frac{1}{2\pi|\Sigma|^{1/2}\delta^{\alpha}} \exp\!\left\{-\frac{a(\textbf{x}) + 2b(\textbf{x})\delta^{\alpha} + c\delta^{2\alpha}}{2\delta^{\alpha}}\right\}.\end{align*}
The proofs of the following three lemmas are given in the appendix.
Lemma 4. For any
![]() $\lambda>0$
there exist
$\lambda>0$
there exist
![]() $\mathcal C_{0},\mathcal C_{1}>0$
such that
$\mathcal C_{0},\mathcal C_{1}>0$
such that
for all
![]() $\delta>0$
sufficiently small.
$\delta>0$
sufficiently small.
In the following lemma, we establish the formulas for
![]() $f^-$
and
$f^-$
and
![]() $g^-$
and show that
$g^-$
and show that
![]() $g^-$
is upper-bounded by
$g^-$
is upper-bounded by
![]() $f^-$
uniformly in
$f^-$
uniformly in
![]() $\delta$
, up to a positive constant.
$\delta$
, up to a positive constant.
Lemma 5. For any
![]() $\lambda>0$
,
$\lambda>0$
,
-
(i)
 $\displaystyle f^-(\boldsymbol{x};\; \delta) = p(\delta)^{-1} f(\boldsymbol{x};\;\delta) \mathbb{1}\{\boldsymbol{x}\leq 0\}$
;
$\displaystyle f^-(\boldsymbol{x};\; \delta) = p(\delta)^{-1} f(\boldsymbol{x};\;\delta) \mathbb{1}\{\boldsymbol{x}\leq 0\}$
; -
(ii)
 $\displaystyle g^-(\boldsymbol{x};\; \delta, \lambda) = q(\delta, \lambda)^{-1}f(\boldsymbol{x};\;\delta) \int_0^\infty \lambda\exp\!\left\{-\frac{cz^2 + 2z((\lambda-c)\delta^{\alpha} - b(\boldsymbol{x}))}{2\delta^{\alpha}}\right\}\textrm{d}z \cdot \mathbb{1}\{\textbf{x}\leq 0\}$
;
$\displaystyle g^-(\boldsymbol{x};\; \delta, \lambda) = q(\delta, \lambda)^{-1}f(\boldsymbol{x};\;\delta) \int_0^\infty \lambda\exp\!\left\{-\frac{cz^2 + 2z((\lambda-c)\delta^{\alpha} - b(\boldsymbol{x}))}{2\delta^{\alpha}}\right\}\textrm{d}z \cdot \mathbb{1}\{\textbf{x}\leq 0\}$
; -
(iii) there exists
 $C>0$
, depending only on
$C>0$
, depending only on
 $\lambda$
, such that for all
$\lambda$
, such that for all
 $\delta$
small enough,
$\delta$
small enough, $\displaystyle g^-(\boldsymbol{x};\; \delta,\lambda) \leq C f^-(\boldsymbol{x};\;\delta)$
for all
$\displaystyle g^-(\boldsymbol{x};\; \delta,\lambda) \leq C f^-(\boldsymbol{x};\;\delta)$
for all
 $\boldsymbol{x}\leq 0$
.
$\boldsymbol{x}\leq 0$
.
Recall the definition of
![]() $\Sigma$
in Equation (10). In what follows, for
$\Sigma$
in Equation (10). In what follows, for
![]() $k\in\mathbb{Z}$
we define
$k\in\mathbb{Z}$
we define
 \begin{equation}\begin{split}{\small\begin{pmatrix}c^-(k) \\[5pt] c^+(k)\end{pmatrix}} & \;:\!=\; \Sigma^{-1} \cdot {\small\begin{pmatrix}\textrm{cov}(Z_\alpha(k), Z_\alpha(\!-\!1))\\[5pt] \textrm{cov}(Z_\alpha(k), Z_\alpha(1))\end{pmatrix}}\\[5pt] & = \frac{1}{2^\alpha(4-2^\alpha)} \cdot {\small\begin{pmatrix}2 & 2^\alpha-2\\[5pt] 2^\alpha-2 & 2 \end{pmatrix}} \cdot {\small\begin{pmatrix}k^\alpha + 1 - (k + \textrm{sgn}(k))^\alpha\\[5pt] k^\alpha + 1 - (k - \textrm{sgn}(k))^\alpha\end{pmatrix}}.\end{split}\end{equation}
\begin{equation}\begin{split}{\small\begin{pmatrix}c^-(k) \\[5pt] c^+(k)\end{pmatrix}} & \;:\!=\; \Sigma^{-1} \cdot {\small\begin{pmatrix}\textrm{cov}(Z_\alpha(k), Z_\alpha(\!-\!1))\\[5pt] \textrm{cov}(Z_\alpha(k), Z_\alpha(1))\end{pmatrix}}\\[5pt] & = \frac{1}{2^\alpha(4-2^\alpha)} \cdot {\small\begin{pmatrix}2 & 2^\alpha-2\\[5pt] 2^\alpha-2 & 2 \end{pmatrix}} \cdot {\small\begin{pmatrix}k^\alpha + 1 - (k + \textrm{sgn}(k))^\alpha\\[5pt] k^\alpha + 1 - (k - \textrm{sgn}(k))^\alpha\end{pmatrix}}.\end{split}\end{equation}
Lemma 6. For
![]() $k\in\mathbb{Z}\setminus\{0\}$
,
$k\in\mathbb{Z}\setminus\{0\}$
,
-
(i)
 $\displaystyle (2-2^{\alpha-1})^{-1} < c^-(k) + c^+(k) \leq 1$
when
$\displaystyle (2-2^{\alpha-1})^{-1} < c^-(k) + c^+(k) \leq 1$
when
 $\alpha\in(0,1)$
;
$\alpha\in(0,1)$
; -
(ii)
 $1 \leq c^-(k) + c^+(k) \leq (2-2^{\alpha-1})^{-1}$
when
$1 \leq c^-(k) + c^+(k) \leq (2-2^{\alpha-1})^{-1}$
when
 $\alpha\in(1,2)$
.
$\alpha\in(1,2)$
.
We are now ready to prove Proposition 2. In what follows, for any
![]() $\delta>0$
and
$\delta>0$
and
![]() $t\in\mathbb{R}$
let
$t\in\mathbb{R}$
let
 \begin{align}Y^\delta_\alpha(t) & \;:\!=\; Z_\alpha(t) - \mathbb{E}\left\{ Z_\alpha(t) \mid (Z_\alpha(\!-\!\delta),Z_\alpha(\delta))\right\} \\[5pt] \nonumber& = Z_\alpha(t) - \big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\big).\end{align}
\begin{align}Y^\delta_\alpha(t) & \;:\!=\; Z_\alpha(t) - \mathbb{E}\left\{ Z_\alpha(t) \mid (Z_\alpha(\!-\!\delta),Z_\alpha(\delta))\right\} \\[5pt] \nonumber& = Z_\alpha(t) - \big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\big).\end{align}
It is a well-known fact that
![]() $\{Y_\alpha^\delta(t), t\in\mathbb{R}\}$
is independent of
$\{Y_\alpha^\delta(t), t\in\mathbb{R}\}$
is independent of
![]() $(Z_\alpha(\!-\!\delta),Z_\alpha(\delta))$
.
$(Z_\alpha(\!-\!\delta),Z_\alpha(\delta))$
.
Proof of Proposition
2. Recall the definition of the events
![]() $A(\delta,\lambda)$
and
$A(\delta,\lambda)$
and
![]() $A(\delta)$
in (7). We have
$A(\delta)$
in (7). We have
 \begin{align*}& \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) + \eta \leq 0 \right \} \\[5pt] & \qquad\qquad = \mathbb{P} \left\{ \text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\Big) + \eta < 0; \ A(\delta, 1) \right \} ,\end{align*}
\begin{align*}& \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) + \eta \leq 0 \right \} \\[5pt] & \qquad\qquad = \mathbb{P} \left\{ \text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\Big) + \eta < 0; \ A(\delta, 1) \right \} ,\end{align*}
with
![]() $Y_\alpha(t)$
as defined in (13). Let
$Y_\alpha(t)$
as defined in (13). Let
![]() $\lambda^* \;:\!=\; 1$
when
$\lambda^* \;:\!=\; 1$
when
![]() $\alpha\in(0,1]$
, and
$\alpha\in(0,1]$
, and
![]() $\lambda^* \;:\!=\; (2-2^{\alpha-1})^{-1}$
when
$\lambda^* \;:\!=\; (2-2^{\alpha-1})^{-1}$
when
![]() $\alpha\in[1,2)$
. By Lemma 6 we have
$\alpha\in[1,2)$
. By Lemma 6 we have
![]() $\lambda^*\geq1$
and
$\lambda^*\geq1$
and
![]() $c^-(k)+c^+(k)\leq \lambda^*$
; thus
$c^-(k)+c^+(k)\leq \lambda^*$
; thus
![]() $A(\delta,1) \subseteq A(\delta,\lambda^*)$
, and the display above is upper-bounded by
$A(\delta,1) \subseteq A(\delta,\lambda^*)$
, and the display above is upper-bounded by
 \begin{align*}& \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)\big(Z_\alpha(\!-\!\delta)+\tfrac{\eta}{\lambda^*}\big) + c^+(k)\big(Z_\alpha(\delta) + \tfrac{\eta}{\lambda^*}\big)\!\!\Big) < 0; \ A(\delta,\lambda^*)\Bigg\}\\[5pt] & = q(\delta,\lambda^*) \cdot \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(\!c^-(k)\big(Z_\alpha(\!-\!\delta)+\tfrac{\eta}{\lambda^*}\big) + c^+(k)\big(Z_\alpha(\delta) + \tfrac{\eta}{\lambda^*}\big)\!\!\Big) < 0 \,\Big\vert\, A(\delta,\lambda^*)\!\Bigg\} \\[5pt] & = q(\delta,\lambda^*) \cdot \int_{\textbf{x}\leq\textbf{0}} \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)x_1 + c^+(k)x_2\Big) < 0\Bigg\}g^-(\textbf{x};\; \delta,\lambda^*)\textrm{d}\textbf{x},\end{align*}
\begin{align*}& \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)\big(Z_\alpha(\!-\!\delta)+\tfrac{\eta}{\lambda^*}\big) + c^+(k)\big(Z_\alpha(\delta) + \tfrac{\eta}{\lambda^*}\big)\!\!\Big) < 0; \ A(\delta,\lambda^*)\Bigg\}\\[5pt] & = q(\delta,\lambda^*) \cdot \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(\!c^-(k)\big(Z_\alpha(\!-\!\delta)+\tfrac{\eta}{\lambda^*}\big) + c^+(k)\big(Z_\alpha(\delta) + \tfrac{\eta}{\lambda^*}\big)\!\!\Big) < 0 \,\Big\vert\, A(\delta,\lambda^*)\!\Bigg\} \\[5pt] & = q(\delta,\lambda^*) \cdot \int_{\textbf{x}\leq\textbf{0}} \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)x_1 + c^+(k)x_2\Big) < 0\Bigg\}g^-(\textbf{x};\; \delta,\lambda^*)\textrm{d}\textbf{x},\end{align*}
where
![]() $g^-$
is as defined in (9). By using Lemma 5(iii), in particular Equation (25), we know that for every
$g^-$
is as defined in (9). By using Lemma 5(iii), in particular Equation (25), we know that for every
![]() $\varepsilon>0$
and all
$\varepsilon>0$
and all
![]() $\delta>0$
small enough, with
$\delta>0$
small enough, with
the expression above is upper-bounded by
 \begin{align*}& q(\delta,\lambda^*) \cdot \int_{\textbf{x}\leq\textbf{0}} \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)x_1 + c^+(k)x_2\Big) < 0\Bigg\}\mathcal C(\delta, \varepsilon)f^-(\textbf{x};\; \delta)\textrm{d}\textbf{x} \\[5pt] & = \mathcal C(\delta,\varepsilon) q(\delta,\lambda^*)\mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\Big) < 0 \,\Big\vert\, A(\delta) \Bigg\} \\[5pt] & = \mathcal C(\delta,\varepsilon) q(\delta,\lambda^*)p(\delta)^{-1} \mathbb P \Bigg\{A(\delta), \text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\Big) < 0\Bigg\} \\[5pt] & = \mathcal C(\delta,\varepsilon) q(\delta,\lambda^*)p(\delta)^{-1} \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) \leq 0 \right \} \\[5pt] & = \tfrac{1}{2}\lambda^*\sqrt{\pi(4-2^\alpha)}(1+\varepsilon) \delta^{\alpha/2} \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) \leq 0 \right \}.\end{align*}
\begin{align*}& q(\delta,\lambda^*) \cdot \int_{\textbf{x}\leq\textbf{0}} \mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)x_1 + c^+(k)x_2\Big) < 0\Bigg\}\mathcal C(\delta, \varepsilon)f^-(\textbf{x};\; \delta)\textrm{d}\textbf{x} \\[5pt] & = \mathcal C(\delta,\varepsilon) q(\delta,\lambda^*)\mathbb P \Bigg\{\text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\Big) < 0 \,\Big\vert\, A(\delta) \Bigg\} \\[5pt] & = \mathcal C(\delta,\varepsilon) q(\delta,\lambda^*)p(\delta)^{-1} \mathbb P \Bigg\{A(\delta), \text{sup}_{k\in\mathbb{Z}\setminus\{-1,0,1\}} Y^\delta_\alpha(\delta k) + \Big(c^-(k)Z_\alpha(\!-\!\delta) + c^+(k)Z_\alpha(\delta)\Big) < 0\Bigg\} \\[5pt] & = \mathcal C(\delta,\varepsilon) q(\delta,\lambda^*)p(\delta)^{-1} \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) \leq 0 \right \} \\[5pt] & = \tfrac{1}{2}\lambda^*\sqrt{\pi(4-2^\alpha)}(1+\varepsilon) \delta^{\alpha/2} \mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) \leq 0 \right \}.\end{align*}
Finally, from [Reference Dieker and Yakir23, Proposition 4] we know that
![]() $\mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) \leq 0 \right \} \sim \delta\mathcal H_\alpha$
; therefore, after substituting for
$\mathbb{P} \left\{ \text{sup}_{t\in\delta\mathbb{Z}\setminus\{0\}} Z_\alpha(t) \leq 0 \right \} \sim \delta\mathcal H_\alpha$
; therefore, after substituting for
![]() $\lambda^*$
, we find that the above is upper-bounded by
$\lambda^*$
, we find that the above is upper-bounded by
for all
![]() $\delta>0$
sufficiently small.
$\delta>0$
sufficiently small.
3.2. Proof of Theorem 1, case
 $\alpha\in (1,2)$
$\alpha\in (1,2)$
The following lemma provides a crucial bound for
![]() $\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta}$
.
$\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta}$
.
Lemma 7. For sufficiently small
![]() $\delta>0$
it holds that
$\delta>0$
it holds that
Proof of Lemma
7. As follows from the proof of [Reference Dębicki, Hashorva and Michna17, Theorem 1], in particular the first equation on p. 12 with
![]() $c_\delta \;:\!=\; [1/\delta]\delta$
, where
$c_\delta \;:\!=\; [1/\delta]\delta$
, where
![]() $[\!\cdot\!]$
is the integer part of a real number, it holds that
$[\!\cdot\!]$
is the integer part of a real number, it holds that
 \begin{align*}\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta} &\le c_\delta^{-1}\mathbb{E}\left\{ \text{sup}_{t\in [0,c_\delta]}e^{Z_\alpha(t)}-\text{sup}_{t\in [0,c_\delta]_\delta}e^{Z_\alpha(t)}\right\}\\[5pt] &\le 2\mathbb{E}\left\{ \text{sup}_{t\in [0,c_\delta]}e^{Z_\alpha(t)}-\text{sup}_{t\in [0,c_\delta]_\delta}e^{Z_\alpha(t)}\right\}\\[5pt] &\le 2\mathbb{E}\left\{ \text{sup}_{t\in [0,1]}e^{Z_\alpha(t)}-\text{sup}_{t\in [0,1]_\delta}e^{Z_\alpha(t)}\right\}. \end{align*}
\begin{align*}\mathcal H_{\alpha} - \mathcal H_{\alpha}^{\delta} &\le c_\delta^{-1}\mathbb{E}\left\{ \text{sup}_{t\in [0,c_\delta]}e^{Z_\alpha(t)}-\text{sup}_{t\in [0,c_\delta]_\delta}e^{Z_\alpha(t)}\right\}\\[5pt] &\le 2\mathbb{E}\left\{ \text{sup}_{t\in [0,c_\delta]}e^{Z_\alpha(t)}-\text{sup}_{t\in [0,c_\delta]_\delta}e^{Z_\alpha(t)}\right\}\\[5pt] &\le 2\mathbb{E}\left\{ \text{sup}_{t\in [0,1]}e^{Z_\alpha(t)}-\text{sup}_{t\in [0,1]_\delta}e^{Z_\alpha(t)}\right\}. \end{align*}
This completes the proof.
Now we are ready to prove Theorem 1(ii).
Proof of Theorem
1,
![]() $\alpha\in (1,2)$
. Note that for any
$\alpha\in (1,2)$
. Note that for any
![]() $ y\le x$
it holds that
$ y\le x$
it holds that
![]() $e^x-e^y\le (x-y)e^x$
. Implementing this inequality, we find that for
$e^x-e^y\le (x-y)e^x$
. Implementing this inequality, we find that for
![]() $s,t\in[0,1]$
,
$s,t\in[0,1]$
,
 \begin{align*}\left|e^{Z_\alpha(t)}-e^{Z_\alpha(s)}\right| &\le e^{\max\!(Z_\alpha(t),Z_\alpha(s))}|Z_\alpha(t)-Z_\alpha(s)|\\[5pt] &\le e^{\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\left|\sqrt 2(B_\alpha(t)-B_\alpha(s))-(t^\alpha-s^\alpha)\right|. \end{align*}
\begin{align*}\left|e^{Z_\alpha(t)}-e^{Z_\alpha(s)}\right| &\le e^{\max\!(Z_\alpha(t),Z_\alpha(s))}|Z_\alpha(t)-Z_\alpha(s)|\\[5pt] &\le e^{\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\left|\sqrt 2(B_\alpha(t)-B_\alpha(s))-(t^\alpha-s^\alpha)\right|. \end{align*}
Next, by Lemma 7 we have
 \begin{align*}\mathcal H_\alpha - \mathcal H_\alpha^\delta & \leq 2\mathbb{E}\left\{ \mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}\left|e^{Z_\alpha(t)}-e^{Z_\alpha(s)}\right|\right\} \\[5pt] & \leq 2\sqrt{2}\mathbb{E}\left\{ e^{\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\text{sup}_{t,s\in [0,1],|t-s|\le\delta}|B_\alpha(t)-B_\alpha(s)|\right\}\\[5pt] & \quad + 2\mathbb{E}\left\{ e^{\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}|t^\alpha-s^\alpha|\right\}.\end{align*}
\begin{align*}\mathcal H_\alpha - \mathcal H_\alpha^\delta & \leq 2\mathbb{E}\left\{ \mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}\left|e^{Z_\alpha(t)}-e^{Z_\alpha(s)}\right|\right\} \\[5pt] & \leq 2\sqrt{2}\mathbb{E}\left\{ e^{\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\text{sup}_{t,s\in [0,1],|t-s|\le\delta}|B_\alpha(t)-B_\alpha(s)|\right\}\\[5pt] & \quad + 2\mathbb{E}\left\{ e^{\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}|t^\alpha-s^\alpha|\right\}.\end{align*}
Clearly, the second term is upper-bounded by
![]() $\mathcal C_1 \delta$
for all
$\mathcal C_1 \delta$
for all
![]() $\delta$
small enough. Using the Hölder inequality, the first term can be bounded by
$\delta$
small enough. Using the Hölder inequality, the first term can be bounded by
 \begin{equation*}2\sqrt{2}\mathbb{E}\left\{ e^{2\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\right\}^{1/2}\mathbb{E}\left\{ \left(\mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}(B_\alpha(t)-B_\alpha(s))\right)^2\right\}^{1/2}.\end{equation*}
\begin{equation*}2\sqrt{2}\mathbb{E}\left\{ e^{2\sqrt 2\max\limits_{w\in [0,1]}B_\alpha(w)}\right\}^{1/2}\mathbb{E}\left\{ \left(\mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}(B_\alpha(t)-B_\alpha(s))\right)^2\right\}^{1/2}.\end{equation*}
The first expectation is finite. The random variable inside the second expectation is called the uniform modulus of continuity. From [Reference Dalang10, Theorem 4.2, p. 164] it follows that there exists
![]() $\mathcal C>0$
such that
$\mathcal C>0$
such that
 \begin{equation*}\mathbb{E}\left\{ \left(\mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}(B_\alpha(t)-B_\alpha(s))\right)^2\right\}^{1/2} \leq \mathcal C\delta^{\alpha/2}|\log\!(\delta)|^{1/2}.\end{equation*}
\begin{equation*}\mathbb{E}\left\{ \left(\mathop{\text{sup}}\limits_{t,s\in [0,1],|t-s|\le\delta}(B_\alpha(t)-B_\alpha(s))\right)^2\right\}^{1/2} \leq \mathcal C\delta^{\alpha/2}|\log\!(\delta)|^{1/2}.\end{equation*}
This concludes the proof.
3.3. Proofs of Theorems 2 and 3
Let
![]() $\delta\geq0$
. Define a measure
$\delta\geq0$
. Define a measure
![]() $\mu_\delta$
such that for real numbers
$\mu_\delta$
such that for real numbers
![]() $a\le b$
,
$a\le b$
,
 \begin{eqnarray*}\mu_\delta([a,b]) =\begin{cases}\delta\cdot \#\{[a,b]_\delta \}, & \delta>0,\\[5pt] b-a, & \delta = 0.\end{cases} \end{eqnarray*}
\begin{eqnarray*}\mu_\delta([a,b]) =\begin{cases}\delta\cdot \#\{[a,b]_\delta \}, & \delta>0,\\[5pt] b-a, & \delta = 0.\end{cases} \end{eqnarray*}
Proof of Theorem
2. For any
![]() $T>0$
,
$T>0$
,
![]() $x\ge 1$
, and
$x\ge 1$
, and
![]() $\delta\ge 0$
, we have
$\delta\ge 0$
, we have
 \begin{align} \mathbb{P} \left\{ \xi_\alpha^\delta>x \right \} &\le \notag\mathbb{P} \left\{ \frac {e^{\text{sup}_{t\in \mathbb{R}}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \}\\[5pt] &=\notag\mathbb{P} \left\{ \frac{e^{\text{sup}_{t\in [\!-\!T,T]}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \textrm{ and } Z_\alpha(t) \textrm{ achieves its maximum at } t \in [\!-\!T,T] \right \}\\[5pt] \notag & \ \ + \mathbb{P} \left\{\frac{e^{\text{sup}_{t\in \mathbb{R}\backslash [\!-\!T,T]}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \textrm{ and } Z_\alpha(t)\textrm{ achieves its maximum at } t \in \mathbb{R}\backslash[\!-\!T,T] \right \}\\[5pt] \notag & \le \mathbb{P} \left\{\frac{e^{\text{sup}_{t\in [\!-\!T,T]}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \}+\mathbb{P} \left\{ \exists t\in \mathbb{R}\backslash [\!-\!T,T]\; :\; Z_\alpha(t)>0 \right \}\\[5pt] \notag &\le\mathbb{P} \left\{\frac{e^{\text{sup}_{t\in [\!-\!T,T]}Z_\alpha(t)}}{\int_{[\!-\!T,T)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} +2\mathbb{P} \left\{ \exists t\ge T \;:\; Z_\alpha(t)>0 \right \}\\[5pt] & \;=\!:\; p_1(T,x)+2p_2(T). \end{align}
\begin{align} \mathbb{P} \left\{ \xi_\alpha^\delta>x \right \} &\le \notag\mathbb{P} \left\{ \frac {e^{\text{sup}_{t\in \mathbb{R}}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \}\\[5pt] &=\notag\mathbb{P} \left\{ \frac{e^{\text{sup}_{t\in [\!-\!T,T]}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \textrm{ and } Z_\alpha(t) \textrm{ achieves its maximum at } t \in [\!-\!T,T] \right \}\\[5pt] \notag & \ \ + \mathbb{P} \left\{\frac{e^{\text{sup}_{t\in \mathbb{R}\backslash [\!-\!T,T]}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \textrm{ and } Z_\alpha(t)\textrm{ achieves its maximum at } t \in \mathbb{R}\backslash[\!-\!T,T] \right \}\\[5pt] \notag & \le \mathbb{P} \left\{\frac{e^{\text{sup}_{t\in [\!-\!T,T]}Z_\alpha(t)}}{\int_\mathbb{R} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \}+\mathbb{P} \left\{ \exists t\in \mathbb{R}\backslash [\!-\!T,T]\; :\; Z_\alpha(t)>0 \right \}\\[5pt] \notag &\le\mathbb{P} \left\{\frac{e^{\text{sup}_{t\in [\!-\!T,T]}Z_\alpha(t)}}{\int_{[\!-\!T,T)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} +2\mathbb{P} \left\{ \exists t\ge T \;:\; Z_\alpha(t)>0 \right \}\\[5pt] & \;=\!:\; p_1(T,x)+2p_2(T). \end{align}
Estimation of
![]() $p_2(T)$
. By the self-similarity of fBm we have
$p_2(T)$
. By the self-similarity of fBm we have
 \begin{align*} \notag p_2(T) &\le \sum_{k=1}^\infty \mathbb{P} \left\{ \exists t \in [kT,(k+1)T]\;:\; \sqrt 2B_\alpha(t)-t^{\alpha}>0 \right \}\\[5pt] &= \notag\sum_{k=1}^\infty \mathbb{P} \left\{ \exists t \in [1,1+\frac{1}{k}]\;:\; \sqrt 2B_\alpha(t)(kT)^{\alpha/2}>(kT)^{\alpha}t^{\alpha} \right \}\\[5pt] &\le \notag\sum_{k=1}^\infty \mathbb{P} \left\{ \exists t \in [1,2]\;:\; \sqrt 2B_\alpha(t)>(kT)^{\alpha/2} \right \}. \end{align*}
\begin{align*} \notag p_2(T) &\le \sum_{k=1}^\infty \mathbb{P} \left\{ \exists t \in [kT,(k+1)T]\;:\; \sqrt 2B_\alpha(t)-t^{\alpha}>0 \right \}\\[5pt] &= \notag\sum_{k=1}^\infty \mathbb{P} \left\{ \exists t \in [1,1+\frac{1}{k}]\;:\; \sqrt 2B_\alpha(t)(kT)^{\alpha/2}>(kT)^{\alpha}t^{\alpha} \right \}\\[5pt] &\le \notag\sum_{k=1}^\infty \mathbb{P} \left\{ \exists t \in [1,2]\;:\; \sqrt 2B_\alpha(t)>(kT)^{\alpha/2} \right \}. \end{align*}
Thus, using the Borell–TIS inequality, we find that for all
![]() $T\ge 1$
,
$T\ge 1$
,
Estimation of
![]() $p_1(T,x)$
. Observe that for
$p_1(T,x)$
. Observe that for
![]() $T,x\ge 1$
and
$T,x\ge 1$
and
![]() $\delta\in[0,1]$
,
$\delta\in[0,1]$
,
 \begin{eqnarray*}p_1(T,x) &\le& \mathbb{P} \left\{\frac{ \sum_{k=-T}^{T-1}e^{\text{sup}_{t\in [k,k+1]}Z_\alpha(t)}}{\sum_{k=-T}^{T-1}\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} \;=\!:\; \mathbb{P} \left\{ \frac{\sum_{k=-T}^{T-1}a_k(\omega)}{\sum_{k=-T}^{T-1}b_k(\omega)}>x \right \} . \end{eqnarray*}
\begin{eqnarray*}p_1(T,x) &\le& \mathbb{P} \left\{\frac{ \sum_{k=-T}^{T-1}e^{\text{sup}_{t\in [k,k+1]}Z_\alpha(t)}}{\sum_{k=-T}^{T-1}\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} \;=\!:\; \mathbb{P} \left\{ \frac{\sum_{k=-T}^{T-1}a_k(\omega)}{\sum_{k=-T}^{T-1}b_k(\omega)}>x \right \} . \end{eqnarray*}
Since the event
![]() $\{\sum_{k=-T}^{T-1}a_k(\omega)/\sum_{k=-T}^{T-1}b_k(\omega)>x\}$
implies
$\{\sum_{k=-T}^{T-1}a_k(\omega)/\sum_{k=-T}^{T-1}b_k(\omega)>x\}$
implies
![]() $\{a_k(\omega)/b_k(\omega)>x, \textrm{ for some } k \in [\!-\!T,T-1]_1\}$
, we have
$\{a_k(\omega)/b_k(\omega)>x, \textrm{ for some } k \in [\!-\!T,T-1]_1\}$
, we have
 \begin{eqnarray*}\mathbb{P} \left\{ \frac{\sum_{k=-T}^{T-1}a_k(\omega)}{\sum_{k=-T}^{T-1}b_k(\omega)}>x \right \} \le\sum_{k=-T}^{T-1}\mathbb{P} \left\{ \frac{a_k(\omega)}{b_k(\omega)}>x \right \}\le 2T \text{sup}_{k \in [\!-\!T,T]}\mathbb{P} \left\{\frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} . \end{eqnarray*}
\begin{eqnarray*}\mathbb{P} \left\{ \frac{\sum_{k=-T}^{T-1}a_k(\omega)}{\sum_{k=-T}^{T-1}b_k(\omega)}>x \right \} \le\sum_{k=-T}^{T-1}\mathbb{P} \left\{ \frac{a_k(\omega)}{b_k(\omega)}>x \right \}\le 2T \text{sup}_{k \in [\!-\!T,T]}\mathbb{P} \left\{\frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} . \end{eqnarray*}
Therefore, we obtain that for
![]() $x,T\ge 1$
$x,T\ge 1$
 \begin{eqnarray*}p_1(T,x) \le 2T \text{sup}_{k \in [\!-\!T,T]}\mathbb{P} \left\{ \frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \}. \end{eqnarray*}
\begin{eqnarray*}p_1(T,x) \le 2T \text{sup}_{k \in [\!-\!T,T]}\mathbb{P} \left\{ \frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \}. \end{eqnarray*}
Next, by the stationarity of the increments of fBm, for
![]() $x,T\ge 1$
we have
$x,T\ge 1$
we have
 \begin{align*}& \mathbb{P} \left\{ \frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} \leq \mathbb{P} \left\{ \frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\mu_\delta[k,k+1]\inf_{[k,k+1]} e^{Z_\alpha(t)}}>x \right \} \\[5pt] & \qquad\qquad\leq \mathbb{P} \left\{ \exists t,s \in [k,k+1]\;:\; Z_\alpha(t)-Z_\alpha(s)>\log\!(\tfrac{x}{2}) \right \} \\[5pt] & \qquad\qquad\leq \mathbb{P} \left\{ \exists t,s \in [k,k+1] \;:\; B_\alpha(t)-B_\alpha(s)>\frac{\log\!(\tfrac{x}{2}) - \text{sup}_{t,s \in [k,k+1]}(|t|^{\alpha}-|s|^{\alpha}) }{\sqrt 2} \right \} \\[5pt] & \qquad\qquad\leq \mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\frac{\log x -\mathcal C\max\!(1,T^{\alpha-1})}{\sqrt 2} \right \} ,\end{align*}
\begin{align*}& \mathbb{P} \left\{ \frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\int_{[k,k+1)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>x \right \} \leq \mathbb{P} \left\{ \frac{\text{sup}_{t\in [k,k+1]}e^{Z_\alpha(t)}}{\mu_\delta[k,k+1]\inf_{[k,k+1]} e^{Z_\alpha(t)}}>x \right \} \\[5pt] & \qquad\qquad\leq \mathbb{P} \left\{ \exists t,s \in [k,k+1]\;:\; Z_\alpha(t)-Z_\alpha(s)>\log\!(\tfrac{x}{2}) \right \} \\[5pt] & \qquad\qquad\leq \mathbb{P} \left\{ \exists t,s \in [k,k+1] \;:\; B_\alpha(t)-B_\alpha(s)>\frac{\log\!(\tfrac{x}{2}) - \text{sup}_{t,s \in [k,k+1]}(|t|^{\alpha}-|s|^{\alpha}) }{\sqrt 2} \right \} \\[5pt] & \qquad\qquad\leq \mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\frac{\log x -\mathcal C\max\!(1,T^{\alpha-1})}{\sqrt 2} \right \} ,\end{align*}
where in the second line we used that
![]() $\mu_\delta[k,k+1]\geq1/2$
for
$\mu_\delta[k,k+1]\geq1/2$
for
![]() $\delta\in[0,1]$
. Thus, for
$\delta\in[0,1]$
. Thus, for
![]() $T,x\ge 1$
,
$T,x\ge 1$
,
Combining the statement above with (14) and (15), for
![]() $x,T\ge1$
we have
$x,T\ge1$
we have
Assume that
![]() $\alpha\le 1$
. Then, choosing
$\alpha\le 1$
. Then, choosing
![]() $T=x$
in the line above, by the Borell–TIS inequality we have for any fixed
$T=x$
in the line above, by the Borell–TIS inequality we have for any fixed
![]() $\varepsilon>0$
and sufficiently large x that
$\varepsilon>0$
and sufficiently large x that
Assume that
![]() $\alpha>1$
. Taking
$\alpha>1$
. Taking
![]() $T = \mathcal C'(\log x)^{\frac{1}{\alpha-1}}$
with sufficiently small
$T = \mathcal C'(\log x)^{\frac{1}{\alpha-1}}$
with sufficiently small
![]() $\mathcal C'>0$
, we obtain by the Borell–TIS inequality that for any fixed
$\mathcal C'>0$
, we obtain by the Borell–TIS inequality that for any fixed
![]() $\varepsilon>0$
and sufficiently large x,
$\varepsilon>0$
and sufficiently large x,
The first claim now follows since
![]() $\mathbb{P} \left\{ \xi_\alpha^\delta(T)>x \right \} =p_1(T,x)$
and
$\mathbb{P} \left\{ \xi_\alpha^\delta(T)>x \right \} =p_1(T,x)$
and
![]() $\frac{\alpha}{\alpha-1}>2$
. The second claims follows in the same way by (17).
$\frac{\alpha}{\alpha-1}>2$
. The second claims follows in the same way by (17).
Proof of Theorem
3. Observe that
![]() $|x^p-y^p| \le p|x-y|(x^{p-1}+y^{p-1})$
for all
$|x^p-y^p| \le p|x-y|(x^{p-1}+y^{p-1})$
for all
![]() $x,y\ge 0$
and
$x,y\ge 0$
and
![]() $p\ge 1$
; this can be shown straightforwardly by differentiation. Hence we have
$p\ge 1$
; this can be shown straightforwardly by differentiation. Hence we have

We have
where
 \begin{align*}\beta_1 &= \frac{\mathop{\text{sup}}\limits_{t\in\delta\mathbb{Z}}e^{Z_\alpha(t)}-\mathop{\text{sup}}\limits_{t\in[\!-\!T,T]_\delta}e^{Z_\alpha(t)}}{\int_{\mathbb{R}}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}\ge 0,\\[5pt] \beta_2 &= \frac{\int_{\mathbb{R}\backslash[\!-\!T,T]}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}{\int_{\mathbb{R}}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>0,\\[5pt] \beta_3 &= \frac{\mathop{\text{sup}}\limits_{t\in[\!-\!T,T]_\delta}e^{Z_\alpha(t)}}{\int_{[\!-\!T,T]}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>0. \end{align*}
\begin{align*}\beta_1 &= \frac{\mathop{\text{sup}}\limits_{t\in\delta\mathbb{Z}}e^{Z_\alpha(t)}-\mathop{\text{sup}}\limits_{t\in[\!-\!T,T]_\delta}e^{Z_\alpha(t)}}{\int_{\mathbb{R}}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}\ge 0,\\[5pt] \beta_2 &= \frac{\int_{\mathbb{R}\backslash[\!-\!T,T]}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}{\int_{\mathbb{R}}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>0,\\[5pt] \beta_3 &= \frac{\mathop{\text{sup}}\limits_{t\in[\!-\!T,T]_\delta}e^{Z_\alpha(t)}}{\int_{[\!-\!T,T]}e^{Z_\alpha(t)}\textrm{d}\mu_\delta}>0. \end{align*}
Applying the Hölder inequality, we obtain
We have by (16) that for
![]() $x,T\ge 1$
,
$x,T\ge 1$
,
which implies that for
![]() $T\ge 1$
,
$T\ge 1$
,
 \begin{align}&\notag\mathbb{E}\left\{ \beta_3^4\right\} = \int_{0}^\infty\mathbb{P} \left\{ \beta_2>x^{1/4} \right \} \textrm{d}x\\[5pt] &\quad \le 2T \int_{0}^\infty\mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\frac{\frac{1}{4}\log x -\mathcal C\max\!(1,T^{\alpha-1})}{\sqrt 2} \right \} \textrm{d}x\\[5pt] &\quad\le\notag 2T\left( \int_0^{\exp(5\mathcal C\max\!(1,T^{\alpha-1}))}1\textrm{d}x+\int_{\exp(5\mathcal C\max\!(1,T^{\alpha-1}))}^\infty\mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\mathcal C_3\log x \right \} \textrm{d}x\right)\\[5pt] &\quad\le \notag\mathcal C_1e^{\mathcal C\max\!(1,T^{\alpha-1})}. \end{align}
\begin{align}&\notag\mathbb{E}\left\{ \beta_3^4\right\} = \int_{0}^\infty\mathbb{P} \left\{ \beta_2>x^{1/4} \right \} \textrm{d}x\\[5pt] &\quad \le 2T \int_{0}^\infty\mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\frac{\frac{1}{4}\log x -\mathcal C\max\!(1,T^{\alpha-1})}{\sqrt 2} \right \} \textrm{d}x\\[5pt] &\quad\le\notag 2T\left( \int_0^{\exp(5\mathcal C\max\!(1,T^{\alpha-1}))}1\textrm{d}x+\int_{\exp(5\mathcal C\max\!(1,T^{\alpha-1}))}^\infty\mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\mathcal C_3\log x \right \} \textrm{d}x\right)\\[5pt] &\quad\le \notag\mathcal C_1e^{\mathcal C\max\!(1,T^{\alpha-1})}. \end{align}
Finally for
![]() $\alpha\in (0,2)$
and
$\alpha\in (0,2)$
and
![]() $T\ge 1$
we have
$T\ge 1$
we have
Next, we focus on the properties of
![]() $\beta_2$
. For
$\beta_2$
. For
![]() $k>0$
and sufficiently large T we have
$k>0$
and sufficiently large T we have
 \begin{align*}&\mathbb{P} \left\{ \int_{[kT,(k+1)T)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta >e^{-\frac{1}{2}T^\alpha k^\alpha} \right \}\le\mathbb{P} \left\{ (T+1) \text{sup}_{t\in[kT,(k+1)T]}e^{Z_\alpha(t)} >e^{-\frac{1}{2}T^\alpha k^\alpha} \right \}\\[5pt] &\quad =\mathbb{P} \left\{ \log\!(T+1)+ \text{sup}_{t\in[kT,(k+1)T]} Z_\alpha(t) > -\frac{1}{2}T^\alpha k^\alpha \right \}\\[5pt] &\quad=\mathbb{P} \left\{ \exists t\in[kT,(k+1)T] \;:\; \frac{B_\alpha(t)}{t^{\alpha/2}} > \frac{t^{\alpha}-\frac{1}{2}T^\alpha k^\alpha-\log\!(T+1)}{\sqrt 2 t^{\alpha/2}} \right \}\\[5pt] &\quad \le\mathbb{P} \left\{ \exists t\in[kT,(k+1)T] \;:\; \frac{B_\alpha(t)}{t^{\alpha/2}} > (Tk)^{\alpha/2}/3 \right \} , \end{align*}
\begin{align*}&\mathbb{P} \left\{ \int_{[kT,(k+1)T)} e^{Z_\alpha(t)}\textrm{d}\mu_\delta >e^{-\frac{1}{2}T^\alpha k^\alpha} \right \}\le\mathbb{P} \left\{ (T+1) \text{sup}_{t\in[kT,(k+1)T]}e^{Z_\alpha(t)} >e^{-\frac{1}{2}T^\alpha k^\alpha} \right \}\\[5pt] &\quad =\mathbb{P} \left\{ \log\!(T+1)+ \text{sup}_{t\in[kT,(k+1)T]} Z_\alpha(t) > -\frac{1}{2}T^\alpha k^\alpha \right \}\\[5pt] &\quad=\mathbb{P} \left\{ \exists t\in[kT,(k+1)T] \;:\; \frac{B_\alpha(t)}{t^{\alpha/2}} > \frac{t^{\alpha}-\frac{1}{2}T^\alpha k^\alpha-\log\!(T+1)}{\sqrt 2 t^{\alpha/2}} \right \}\\[5pt] &\quad \le\mathbb{P} \left\{ \exists t\in[kT,(k+1)T] \;:\; \frac{B_\alpha(t)}{t^{\alpha/2}} > (Tk)^{\alpha/2}/3 \right \} , \end{align*}
which, by the Borell–TIS inequality, is upper-bounded by
![]() $e^{-k^{\alpha}T^{\alpha}/19}$
. By the lines above we obtain that with probability at least
$e^{-k^{\alpha}T^{\alpha}/19}$
. By the lines above we obtain that with probability at least
![]() $1-\sum_{k\in \mathbb{Z}\backslash\{0\}}e^{-|k|^{\alpha}T^{\alpha}/19}\ge 1-e^{-T^{\alpha}/20}$
, for large T,
$1-\sum_{k\in \mathbb{Z}\backslash\{0\}}e^{-|k|^{\alpha}T^{\alpha}/19}\ge 1-e^{-T^{\alpha}/20}$
, for large T,
Putting everything together, we find that for sufficiently large T,
Next we notice that for
![]() $T\geq1$
,
$T\geq1$
,
so, by the Borell–TIS inequality, the above is bounded by
![]() $e^{-\frac{T^{2\alpha}}{65}}$
for all sufficiently large T. This result in combination with (21) gives us
$e^{-\frac{T^{2\alpha}}{65}}$
for all sufficiently large T. This result in combination with (21) gives us
![]() $\mathbb{P} \left\{ \beta_2>e^{-T^\alpha/12 } \right \} \le e^{-T^\alpha/21}$
for all sufficiently large T. Thus, since
$\mathbb{P} \left\{ \beta_2>e^{-T^\alpha/12 } \right \} \le e^{-T^\alpha/21}$
for all sufficiently large T. Thus, since
![]() $\beta_2\in [0,1]$
, from the line above we immediately obtain that
$\beta_2\in [0,1]$
, from the line above we immediately obtain that
for
![]() $T\ge 1$
. By (15) we observe that
$T\ge 1$
. By (15) we observe that
Next, by Theorem 2, for
![]() $x\ge 1$
we have
$x\ge 1$
we have
and thus
![]() $\mathbb{E}\left\{ \beta_1^4\right\}<\mathcal C$
for a positive constant
$\mathbb{E}\left\{ \beta_1^4\right\}<\mathcal C$
for a positive constant
![]() $\mathcal C$
that does not depend on T. With
$\mathcal C$
that does not depend on T. With
![]() $A_T\;:\!=\; \{\beta_1(\omega)>0\}$
, by the Hölder inequality, for large T we have
$A_T\;:\!=\; \{\beta_1(\omega)>0\}$
, by the Hölder inequality, for large T we have
By the line above and (20), (22), and (18), for
![]() $T\ge 1$
we obtain
$T\ge 1$
we obtain
Our next aim is to estimate
![]() $\mathbb{E}\left\{ \kappa_{p}\right\}$
. We have for
$\mathbb{E}\left\{ \kappa_{p}\right\}$
. We have for
![]() $T\ge 1$
that
$T\ge 1$
that
 \begin{eqnarray*}\mathbb{E}\left\{ (\xi_\alpha^\delta(T))^{2p-2}\right\} &=& \int_0^\infty\mathbb{P} \left\{ \xi_\alpha^\delta(T)>x^{\frac{1}{2p-2}} \right \} \textrm{d}x =\int_0^\infty\mathbb{P} \left\{ p_1(T,x^{\frac{1}{2p-2}}) \right \} \textrm{d}x\\[5pt] &\le &\int_{0}^\infty\mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\frac{\log x^{\frac{1}{2p-2}} -\mathcal C\max\!(1,T^{\alpha-1})}{\sqrt 2} \right \} \textrm{d}x. \end{eqnarray*}
\begin{eqnarray*}\mathbb{E}\left\{ (\xi_\alpha^\delta(T))^{2p-2}\right\} &=& \int_0^\infty\mathbb{P} \left\{ \xi_\alpha^\delta(T)>x^{\frac{1}{2p-2}} \right \} \textrm{d}x =\int_0^\infty\mathbb{P} \left\{ p_1(T,x^{\frac{1}{2p-2}}) \right \} \textrm{d}x\\[5pt] &\le &\int_{0}^\infty\mathbb{P} \left\{ \exists t \in [0,1]\;:\; B_\alpha(t)>\frac{\log x^{\frac{1}{2p-2}} -\mathcal C\max\!(1,T^{\alpha-1})}{\sqrt 2} \right \} \textrm{d}x. \end{eqnarray*}
By the same arguments as in Equation (19), the last integral above does not exceed
![]() $\mathcal C_1e^{\max \mathcal C_2(T^{\alpha-1},1)}$
, and since Theorem 2 implies that
$\mathcal C_1e^{\max \mathcal C_2(T^{\alpha-1},1)}$
, and since Theorem 2 implies that
![]() $\xi_\alpha^\delta$
has all finite moments uniformly bounded for all
$\xi_\alpha^\delta$
has all finite moments uniformly bounded for all
![]() $\delta\ge 0$
, we obtain for
$\delta\ge 0$
, we obtain for
![]() $T\ge 1$
that
$T\ge 1$
that
Combining the bound above with (23), we have
![]() $\sqrt 2 p\mathbb{E}\left\{ \beta^2\right\}\mathbb{E}\left\{ \kappa_{p}\right\} \le e^{-\mathcal C_pT^\alpha}$
for sufficiently large T, and the claim follows.
$\sqrt 2 p\mathbb{E}\left\{ \beta^2\right\}\mathbb{E}\left\{ \kappa_{p}\right\} \le e^{-\mathcal C_pT^\alpha}$
for sufficiently large T, and the claim follows.
3.4. Proofs of Corollaries 1 and 2
In the following,
![]() $\phi$
stands for the probability density function of a standard Gaussian random variable and
$\phi$
stands for the probability density function of a standard Gaussian random variable and
 \begin{align*} v(\eta) \;:\!=\; \eta\exp\!\left(2\sum_{k=1}^\infty \frac{\Psi(\sqrt {\eta k/2})}{k}\right), \qquad \eta>0,\end{align*}
\begin{align*} v(\eta) \;:\!=\; \eta\exp\!\left(2\sum_{k=1}^\infty \frac{\Psi(\sqrt {\eta k/2})}{k}\right), \qquad \eta>0,\end{align*}
with (recall)
![]() $\Psi$
the survival function of a standard Gaussian random variable. Before giving the proofs we introduce the following auxiliary lemma, whose proof is given in the appendix.
$\Psi$
the survival function of a standard Gaussian random variable. Before giving the proofs we introduce the following auxiliary lemma, whose proof is given in the appendix.
Lemma 8. It holds that for any
![]() $\eta>0$
,
$\eta>0$
,
 \begin{eqnarray*} v'(\eta) = \exp\!\left(2\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k} \right)\left(1-\frac{\sqrt \eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k}\right). \end{eqnarray*}
\begin{eqnarray*} v'(\eta) = \exp\!\left(2\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k} \right)\left(1-\frac{\sqrt \eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k}\right). \end{eqnarray*}
Proof of Corollary
1,
![]() $\alpha=1$
. By Proposition 1(i), we find that
$\alpha=1$
. By Proposition 1(i), we find that
Since
![]() $\mathcal H_\eta = v(\eta)^{-1} \to 1$
as
$\mathcal H_\eta = v(\eta)^{-1} \to 1$
as
![]() $\eta \to 0$
(see, e.g., [Reference Dieker and Yakir23]), we conclude that
$\eta \to 0$
(see, e.g., [Reference Dieker and Yakir23]), we conclude that
![]() $\lim_{\eta\to 0} v(\eta)=1$
and hence
$\lim_{\eta\to 0} v(\eta)=1$
and hence
![]() $\mathcal A = \lim_{\eta \to 0}\frac{v(\eta)-1}{\sqrt \eta}.$
Implementing L’Hôpital’s rule, we obtain by Lemma 8 that
$\mathcal A = \lim_{\eta \to 0}\frac{v(\eta)-1}{\sqrt \eta}.$
Implementing L’Hôpital’s rule, we obtain by Lemma 8 that
 \begin{eqnarray*} \mathcal A =\lim_{\eta \to 0} \frac{v'(\eta)}{1/(2\sqrt \eta)}= 2\lim_{\eta \to 0}\sqrt\eta \exp\!\left(2\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\right)\left(1-\frac{\sqrt \eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k}\right). \end{eqnarray*}
\begin{eqnarray*} \mathcal A =\lim_{\eta \to 0} \frac{v'(\eta)}{1/(2\sqrt \eta)}= 2\lim_{\eta \to 0}\sqrt\eta \exp\!\left(2\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\right)\left(1-\frac{\sqrt \eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k}\right). \end{eqnarray*}
Note that by the definition of
![]() $v(\eta)$
, the observation that
$v(\eta)$
, the observation that
![]() $\lim_{\eta\to 0}v(\eta) = 1$
implies
$\lim_{\eta\to 0}v(\eta) = 1$
implies
 \begin{align*}\sqrt\eta \exp\bigg(2\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\bigg)\sim \frac{1}{\sqrt \eta}, \quad \eta \to 0,\end{align*}
\begin{align*}\sqrt\eta \exp\bigg(2\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\bigg)\sim \frac{1}{\sqrt \eta}, \quad \eta \to 0,\end{align*}
and hence, with
![]() $x \;:\!=\; \sqrt \eta/2$
,
$x \;:\!=\; \sqrt \eta/2$
,
where
![]() $\textrm{Li}_{\frac{1}{2}}$
is the polylogarithm function; see, e.g., [Reference Cvijović9]. As follows from [Reference Wood35, Equation (9.3)],
$\textrm{Li}_{\frac{1}{2}}$
is the polylogarithm function; see, e.g., [Reference Cvijović9]. As follows from [Reference Wood35, Equation (9.3)],
 \begin{align*}&\lim_{x\to 0}\frac{1}{x}\Big(1-\frac{x}{\sqrt \pi}\textrm{Li}_{\frac{1}{2}}(e^{-x^2})\Big) \\[5pt] &\quad =\lim_{x\to 0}\frac{1}{x}\Big(1-\frac{x}{\sqrt \pi}\Big(\Gamma(1/2)(x^2)^{-1/2}+\zeta(1/2)+\sum_{k=1}^\infty\zeta(1/2-k)\frac{(\!-\!x^2)^k}{k!} \Big)\Big)\\[5pt] &\quad =\frac{\zeta(1/2)}{\sqrt \pi}-\frac{1}{\sqrt \pi}\lim_{x\to 0}\Big(\sum_{k=1}^\infty\zeta(1/2-k)\frac{x^{2k}(\!-\!1)^k}{k!}\Big). \end{align*}
\begin{align*}&\lim_{x\to 0}\frac{1}{x}\Big(1-\frac{x}{\sqrt \pi}\textrm{Li}_{\frac{1}{2}}(e^{-x^2})\Big) \\[5pt] &\quad =\lim_{x\to 0}\frac{1}{x}\Big(1-\frac{x}{\sqrt \pi}\Big(\Gamma(1/2)(x^2)^{-1/2}+\zeta(1/2)+\sum_{k=1}^\infty\zeta(1/2-k)\frac{(\!-\!x^2)^k}{k!} \Big)\Big)\\[5pt] &\quad =\frac{\zeta(1/2)}{\sqrt \pi}-\frac{1}{\sqrt \pi}\lim_{x\to 0}\Big(\sum_{k=1}^\infty\zeta(1/2-k)\frac{x^{2k}(\!-\!1)^k}{k!}\Big). \end{align*}
Thus, to prove the claim it is enough to show that
By the Riemann functional equation (see [Reference Guariglia25, Equation (2.3)]) and the observation that
![]() $\zeta(s)$
is strictly decreasing for real
$\zeta(s)$
is strictly decreasing for real
![]() $s>1$
, we have for any natural number k that
$s>1$
, we have for any natural number k that
Thus, for
![]() $|x|<1$
we have
$|x|<1$
we have
and (24) follows, which completes the proof of the first statement.
For the statement (ii), by Proposition 1(ii) we have, as
![]() $\delta\to 0$
,
$\delta\to 0$
,
 \begin{align*}\mathcal H_2-\mathcal H_2^\delta &=\frac{1}{\sqrt\pi}-\frac{2}{\delta}\left(\Phi(\frac{\delta}{\sqrt 2})-\frac{1}{2}\right) = \frac{1}{\sqrt \pi}\left(1- \frac{\sqrt 2}{\delta}\int^{\delta/\sqrt 2}_0 e^{-x^2/2}\textrm{d}x\right) \\[5pt] &= \frac{1}{\sqrt \pi}\left(1- \frac{\sqrt 2}{\delta}\int^{\delta/\sqrt 2}_0\left(1-\frac{x^2}{2}\right)\textrm{d}x+O(\delta^4)\right)= \frac{1}{12\sqrt\pi}, \end{align*}
\begin{align*}\mathcal H_2-\mathcal H_2^\delta &=\frac{1}{\sqrt\pi}-\frac{2}{\delta}\left(\Phi(\frac{\delta}{\sqrt 2})-\frac{1}{2}\right) = \frac{1}{\sqrt \pi}\left(1- \frac{\sqrt 2}{\delta}\int^{\delta/\sqrt 2}_0 e^{-x^2/2}\textrm{d}x\right) \\[5pt] &= \frac{1}{\sqrt \pi}\left(1- \frac{\sqrt 2}{\delta}\int^{\delta/\sqrt 2}_0\left(1-\frac{x^2}{2}\right)\textrm{d}x+O(\delta^4)\right)= \frac{1}{12\sqrt\pi}, \end{align*}
and the claim follows.
Proof of Corollary
2. Case
![]() $\alpha=1$
. First we show that
$\alpha=1$
. First we show that
![]() $v(\eta)$
is an increasing function for
$v(\eta)$
is an increasing function for
![]() $\eta> 0$
, which is equivalent to the fact that
$\eta> 0$
, which is equivalent to the fact that
![]() $v'(\eta)>0$
for
$v'(\eta)>0$
for
![]() $\eta>0$
. In light of Lemma 8 it is sufficient to show that
$\eta>0$
. In light of Lemma 8 it is sufficient to show that
 \begin{eqnarray*} \frac{\sqrt \eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k}<1,\quad \eta>0. \end{eqnarray*}
\begin{eqnarray*} \frac{\sqrt \eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k}<1,\quad \eta>0. \end{eqnarray*}
We have
 \begin{align*}\frac{\sqrt\eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k} < \frac{1}{\sqrt \pi} \sqrt{\frac{\eta}{4}}\int_0^\infty e^{-\frac{\eta z}{4}}z^{-1/2}dz &=\frac{1}{\sqrt{\pi}}\int_0^\infty e^{-\frac{\eta z}{4}}(\frac{\eta z}{4})^{-1/2}d(\frac{\eta z}{4}) \\[5pt] &=\frac{1}{\sqrt{\pi}}\Gamma(1/2) = 1, \end{align*}
\begin{align*}\frac{\sqrt\eta}{2\sqrt \pi}\sum_{k=1}^\infty \frac{e^{-\frac{\eta k}{4}}}{\sqrt k} < \frac{1}{\sqrt \pi} \sqrt{\frac{\eta}{4}}\int_0^\infty e^{-\frac{\eta z}{4}}z^{-1/2}dz &=\frac{1}{\sqrt{\pi}}\int_0^\infty e^{-\frac{\eta z}{4}}(\frac{\eta z}{4})^{-1/2}d(\frac{\eta z}{4}) \\[5pt] &=\frac{1}{\sqrt{\pi}}\Gamma(1/2) = 1, \end{align*}
and hence
![]() $\mathcal{H}^{\eta}_1 =1/v(\eta)$
is decreasing for
$\mathcal{H}^{\eta}_1 =1/v(\eta)$
is decreasing for
![]() $\eta>0$
. Since, by the classical definition,
$\eta>0$
. Since, by the classical definition,
![]() $\mathcal{H}_{1}^0>\mathcal{H}_1^{\eta}$
for any
$\mathcal{H}_{1}^0>\mathcal{H}_1^{\eta}$
for any
![]() $\eta>0$
, we obtain the claim.
$\eta>0$
, we obtain the claim.
Case
![]() $\alpha =2$
. By Proposition 1(ii) we have
$\alpha =2$
. By Proposition 1(ii) we have
where
![]() $\eta = \delta/\sqrt 2$
. The derivative of the last integral above with respect to
$\eta = \delta/\sqrt 2$
. The derivative of the last integral above with respect to
![]() $\eta$
equals
$\eta$
equals
and the claim follows.
Appendix
Proof of Equation (6). Let
![]() $t,s\in\mathbb{R}$
be fixed, and let
$t,s\in\mathbb{R}$
be fixed, and let
We will show that
![]() $\delta\mapsto c(\delta;\;t,s)$
is a nondecreasing function, which will conclude the proof. We have
$\delta\mapsto c(\delta;\;t,s)$
is a nondecreasing function, which will conclude the proof. We have
We consider two cases: (i)
![]() $t,s>0$
, and (ii)
$t,s>0$
, and (ii)
![]() $s<0<t$
. Consider case (i) first. Without loss of generality we assume that
$s<0<t$
. Consider case (i) first. Without loss of generality we assume that
![]() $t\geq s$
; then
$t\geq s$
; then
It suffices to show that the first derivative of
![]() $\delta\mapsto c(\delta;\;t,s)$
is nonnegative. We have
$\delta\mapsto c(\delta;\;t,s)$
is nonnegative. We have
where
![]() $x \;:\!=\; \frac{s+\delta}{t+\delta} \in (0,1]$
. The derivative above is nonnegative if and only if
$x \;:\!=\; \frac{s+\delta}{t+\delta} \in (0,1]$
. The derivative above is nonnegative if and only if
![]() $G_1(x,\alpha) \;:\!=\;$
$G_1(x,\alpha) \;:\!=\;$
![]() $(1-x)^{\alpha-1}(1+x) + x^{\alpha} - 1 \geq 0$
for all
$(1-x)^{\alpha-1}(1+x) + x^{\alpha} - 1 \geq 0$
for all
![]() $x\in(0,1]$
. It is easy to see that, for any fixed
$x\in(0,1]$
. It is easy to see that, for any fixed
![]() $x\in(0,1]$
,
$x\in(0,1]$
,
![]() $\alpha\mapsto G_1(x,\alpha)$
is a nondecreasing function; this observation combined with the fact that
$\alpha\mapsto G_1(x,\alpha)$
is a nondecreasing function; this observation combined with the fact that
![]() $G(x,2)=0$
completes the proof of case (i). In case (ii) we need to show that
$G(x,2)=0$
completes the proof of case (i). In case (ii) we need to show that
is a nondecreasing function of x for any
![]() $s,t>0$
. Without loss of generality let
$s,t>0$
. Without loss of generality let
![]() $0<s\leq t$
. Again, we take the first derivative of the above and see that
$0<s\leq t$
. Again, we take the first derivative of the above and see that
where
![]() $x \;:\!=\; \frac{s+\delta}{t+\delta}\in(0,1]$
. The derivative above is nonnegative if and only if
$x \;:\!=\; \frac{s+\delta}{t+\delta}\in(0,1]$
. The derivative above is nonnegative if and only if
![]() $G_2(x,\alpha) \;:\!=\;$
$G_2(x,\alpha) \;:\!=\;$
![]() $(1-x)(1+x)^{\alpha-1} + x^\alpha - 1 \geq 0$
. Notice that
$(1-x)(1+x)^{\alpha-1} + x^\alpha - 1 \geq 0$
. Notice that
![]() $G_2(x,1) = 0$
. We will now show that
$G_2(x,1) = 0$
. We will now show that
![]() $\frac{\partial}{\partial\alpha}G_2(x,\alpha) \leq 0$
for all
$\frac{\partial}{\partial\alpha}G_2(x,\alpha) \leq 0$
for all
![]() $\alpha\in[0,1]$
and
$\alpha\in[0,1]$
and
![]() $x\in(0,1]$
, which will conclude the proof. We have
$x\in(0,1]$
, which will conclude the proof. We have
 \begin{align*}\frac{\partial}{\partial\alpha}G_2(x,\alpha) & = (1-x)(1+x)^{\alpha-1}\log\!(x+1)+x^\alpha\log x \\[5pt] & \leq (1-x)x^{\alpha-1}\log\!(x+1)+x^\alpha\log x \\[5pt] & = x^{\alpha-1}((1-x)\log\!(x+1)+x\log x) \\[5pt] & \leq x^{\alpha-1}((1-x)x + x(x-1)) = 0,\end{align*}
\begin{align*}\frac{\partial}{\partial\alpha}G_2(x,\alpha) & = (1-x)(1+x)^{\alpha-1}\log\!(x+1)+x^\alpha\log x \\[5pt] & \leq (1-x)x^{\alpha-1}\log\!(x+1)+x^\alpha\log x \\[5pt] & = x^{\alpha-1}((1-x)\log\!(x+1)+x\log x) \\[5pt] & \leq x^{\alpha-1}((1-x)x + x(x-1)) = 0,\end{align*}
where in the last line we used the fact that
![]() $\log\!(1+x)\leq x$
for all
$\log\!(1+x)\leq x$
for all
![]() $x>-1$
.
$x>-1$
.
Proof of Lemma 4. For the lower bound, observe that
 \begin{align*}q(\delta, \lambda) & = \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!\delta) -\delta^\alpha+ \lambda^{-1}\eta < 0, \sqrt{2}B_\alpha(\delta) -\delta^\alpha+ \lambda^{-1}\eta < 0) \right \} \\[5pt] & \geq \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!\delta) + \lambda^{-1}\eta < 0, \sqrt{2}B_\alpha(\delta) + \lambda^{-1}\eta < 0, \lambda^{-1}\eta < \delta^{\alpha/2} \right \} \\[5pt] & \geq \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!\delta) < -\delta^{\alpha/2}, \sqrt{2}B_\alpha(\delta) < -\delta^{\alpha/2}, \lambda^{-1}\eta < \delta^{\alpha/2} \right \} \\[5pt] & = \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!1) > 1, \sqrt{2}B_\alpha(1) > 1 \right \} \mathbb{P} \left\{ \lambda^{-1}\eta < \delta^{\alpha/2} \right \} \\[5pt] & = \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!1) > 1, \sqrt{2}B_\alpha(1) > 1 \right \} \cdot \left(1-\exp\!\left\{-\lambda\delta^{\alpha/2}\right\}\right),\end{align*}
\begin{align*}q(\delta, \lambda) & = \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!\delta) -\delta^\alpha+ \lambda^{-1}\eta < 0, \sqrt{2}B_\alpha(\delta) -\delta^\alpha+ \lambda^{-1}\eta < 0) \right \} \\[5pt] & \geq \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!\delta) + \lambda^{-1}\eta < 0, \sqrt{2}B_\alpha(\delta) + \lambda^{-1}\eta < 0, \lambda^{-1}\eta < \delta^{\alpha/2} \right \} \\[5pt] & \geq \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!\delta) < -\delta^{\alpha/2}, \sqrt{2}B_\alpha(\delta) < -\delta^{\alpha/2}, \lambda^{-1}\eta < \delta^{\alpha/2} \right \} \\[5pt] & = \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!1) > 1, \sqrt{2}B_\alpha(1) > 1 \right \} \mathbb{P} \left\{ \lambda^{-1}\eta < \delta^{\alpha/2} \right \} \\[5pt] & = \mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!1) > 1, \sqrt{2}B_\alpha(1) > 1 \right \} \cdot \left(1-\exp\!\left\{-\lambda\delta^{\alpha/2}\right\}\right),\end{align*}
which behaves like
![]() $\lambda\delta^{\alpha/2}\mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!1) > 1, \sqrt{2}B_\alpha(1) > 1 \right \} $
as
$\lambda\delta^{\alpha/2}\mathbb{P} \left\{ \sqrt{2}B_\alpha(\!-\!1) > 1, \sqrt{2}B_\alpha(1) > 1 \right \} $
as
![]() $\delta\downarrow0$
. For the upper bound, observe that
$\delta\downarrow0$
. For the upper bound, observe that
 \begin{align*}q(\delta, \lambda) & \leq \mathbb{P} \left\{ Z_\alpha(\delta) + \lambda^{-1}\eta < 0 \right \} = \mathbb{P} \left\{ \delta^{\alpha/2}\sqrt{2}B_\alpha(1) - \delta^\alpha + \lambda^{-1}\eta < 0 \right \} \\[5pt] & = \int_0^\infty \Phi\left(\tfrac{\delta^\alpha-z}{\sqrt{2}\delta^{\alpha/2}}\right)\lambda e^{-\lambda z}\textrm{d}z \leq \sqrt{2}\delta^{\alpha/2}\lambda\int_0^\infty\Phi\left(\tfrac{\delta^{\alpha/2}}{\sqrt{2}}-z\right)\textrm{d}z \\[5pt] & \leq \sqrt{2}\delta^{\alpha/2}\lambda\left(\tfrac{\delta^{\alpha/2}}{\sqrt{2}} + \int_{0}^{\infty}\Psi(z)\textrm{d}z\right) = \delta^{\alpha/2}\lambda\left(\delta^{\alpha/2} + \frac{\mathbb E|\mathcal N(0,1)|}{\sqrt{2}}\right),\end{align*}
\begin{align*}q(\delta, \lambda) & \leq \mathbb{P} \left\{ Z_\alpha(\delta) + \lambda^{-1}\eta < 0 \right \} = \mathbb{P} \left\{ \delta^{\alpha/2}\sqrt{2}B_\alpha(1) - \delta^\alpha + \lambda^{-1}\eta < 0 \right \} \\[5pt] & = \int_0^\infty \Phi\left(\tfrac{\delta^\alpha-z}{\sqrt{2}\delta^{\alpha/2}}\right)\lambda e^{-\lambda z}\textrm{d}z \leq \sqrt{2}\delta^{\alpha/2}\lambda\int_0^\infty\Phi\left(\tfrac{\delta^{\alpha/2}}{\sqrt{2}}-z\right)\textrm{d}z \\[5pt] & \leq \sqrt{2}\delta^{\alpha/2}\lambda\left(\tfrac{\delta^{\alpha/2}}{\sqrt{2}} + \int_{0}^{\infty}\Psi(z)\textrm{d}z\right) = \delta^{\alpha/2}\lambda\left(\delta^{\alpha/2} + \frac{\mathbb E|\mathcal N(0,1)|}{\sqrt{2}}\right),\end{align*}
where (recall)
![]() $\Phi(\!\cdot\!), \Psi(\!\cdot\!)$
are the CDF and complementary CDF, respectively, of the standard normal distribution. This concludes the proof.
$\Phi(\!\cdot\!), \Psi(\!\cdot\!)$
are the CDF and complementary CDF, respectively, of the standard normal distribution. This concludes the proof.
Proof of Lemma 5. Part (i) follows directly from the definition. For part (ii),
for
![]() $\textbf{x}\leq0$
we have
$\textbf{x}\leq0$
we have
 \begin{align*}g^{-}(\textbf{x};\;\delta,\lambda) & = q(\delta, \lambda)^{-1}\int_0^\infty f(\textbf{x}-{\textbf{1}}_2z;\; \delta)\cdot \lambda\textrm{e}^{-\lambda z} \textrm{d}z \\[5pt] & = \int_0^\infty\frac{q(\delta, \lambda)^{-1}}{2\pi|\Sigma|\delta^{\alpha}}\exp\!\left\{-\frac{(\textbf{x}+{\textbf{1}}_2(\delta^\alpha-z))^\top\Sigma^{-1}(\textbf{x}+{\textbf{1}}_2(\delta^\alpha-z))}{2\delta^{\alpha}}\right\}\cdot \lambda\textrm{e}^{-\lambda z} \textrm{d}z \\[5pt] & = \int_0^\infty\frac{\lambda q(\delta, \lambda)^{-1}}{2\pi|\Sigma|\delta^{\alpha}}\exp\!\left\{-\frac{a(\textbf{x}) + 2b(\textbf{x})(\delta^\alpha-z) + c(\delta^{2\alpha}-2\delta^\alpha z + z^2) + 2\lambda\delta^\alpha z}{2\delta^{\alpha}}\right\} \textrm{d}z \\[5pt] & = q(\delta, \lambda)^{-1}f(\textbf{x};\; \delta)\int_0^\infty \lambda \exp\!\left\{-\frac{cz^2 + 2z((\lambda-c)\delta^\alpha - b(\textbf{x}))}{2\delta^{\alpha}}\right\} \textrm{d}z.\end{align*}
\begin{align*}g^{-}(\textbf{x};\;\delta,\lambda) & = q(\delta, \lambda)^{-1}\int_0^\infty f(\textbf{x}-{\textbf{1}}_2z;\; \delta)\cdot \lambda\textrm{e}^{-\lambda z} \textrm{d}z \\[5pt] & = \int_0^\infty\frac{q(\delta, \lambda)^{-1}}{2\pi|\Sigma|\delta^{\alpha}}\exp\!\left\{-\frac{(\textbf{x}+{\textbf{1}}_2(\delta^\alpha-z))^\top\Sigma^{-1}(\textbf{x}+{\textbf{1}}_2(\delta^\alpha-z))}{2\delta^{\alpha}}\right\}\cdot \lambda\textrm{e}^{-\lambda z} \textrm{d}z \\[5pt] & = \int_0^\infty\frac{\lambda q(\delta, \lambda)^{-1}}{2\pi|\Sigma|\delta^{\alpha}}\exp\!\left\{-\frac{a(\textbf{x}) + 2b(\textbf{x})(\delta^\alpha-z) + c(\delta^{2\alpha}-2\delta^\alpha z + z^2) + 2\lambda\delta^\alpha z}{2\delta^{\alpha}}\right\} \textrm{d}z \\[5pt] & = q(\delta, \lambda)^{-1}f(\textbf{x};\; \delta)\int_0^\infty \lambda \exp\!\left\{-\frac{cz^2 + 2z((\lambda-c)\delta^\alpha - b(\textbf{x}))}{2\delta^{\alpha}}\right\} \textrm{d}z.\end{align*}
For part (iii), we have
![]() $\Sigma^{-1} = \big(2^\alpha(4-2^\alpha)\big)^{-1} \cdot \left(\begin{smallmatrix}2 & 2^\alpha-2\\[5pt] 2^\alpha-2 & 2 \end{smallmatrix}\right)$
; thus
$\Sigma^{-1} = \big(2^\alpha(4-2^\alpha)\big)^{-1} \cdot \left(\begin{smallmatrix}2 & 2^\alpha-2\\[5pt] 2^\alpha-2 & 2 \end{smallmatrix}\right)$
; thus
![]() $\Sigma^{-1}{\textbf{1}}_2 \geq \textbf{0}$
element-wise. It then follows that
$\Sigma^{-1}{\textbf{1}}_2 \geq \textbf{0}$
element-wise. It then follows that
![]() $b(\textbf{x}) \leq \textbf{0}$
for all
$b(\textbf{x}) \leq \textbf{0}$
for all
![]() $\textbf{x}\leq \textbf{0}$
. Since
$\textbf{x}\leq \textbf{0}$
. Since
![]() $g^{-}$
is nonzero only on
$g^{-}$
is nonzero only on
![]() $\textbf{x} \leq \textbf{0}$
, this yields the following upper bound:
$\textbf{x} \leq \textbf{0}$
, this yields the following upper bound:
Now, after applying the substitution
![]() $z \;:\!=\; \delta^{\alpha/2} z$
, we find that for any
$z \;:\!=\; \delta^{\alpha/2} z$
, we find that for any
![]() $\varepsilon>0$
and all
$\varepsilon>0$
and all
![]() $\delta$
small enough,
$\delta$
small enough,
 \begin{align*}\int_0^\infty \lambda \exp\!\left\{-\frac{cz^2 + 2z(\lambda-c)\delta^\alpha}{2\delta^{\alpha}}\right\} \textrm{d}z & = \int_0^\infty \lambda\delta^{\alpha/2} \exp\!\left\{-\frac{cz^2 + 2\delta^{\alpha/2}z(\lambda-c)}{2} \right\} \textrm{d}z \\[5pt] & < \frac{\lambda\sqrt{\pi}}{\sqrt{2c}}((1+\varepsilon) \cdot \delta^{\alpha/2}.\end{align*}
\begin{align*}\int_0^\infty \lambda \exp\!\left\{-\frac{cz^2 + 2z(\lambda-c)\delta^\alpha}{2\delta^{\alpha}}\right\} \textrm{d}z & = \int_0^\infty \lambda\delta^{\alpha/2} \exp\!\left\{-\frac{cz^2 + 2\delta^{\alpha/2}z(\lambda-c)}{2} \right\} \textrm{d}z \\[5pt] & < \frac{\lambda\sqrt{\pi}}{\sqrt{2c}}((1+\varepsilon) \cdot \delta^{\alpha/2}.\end{align*}
Hence, using part (i) and substituting
![]() $c = 2/(4-2^\alpha)$
as in Equation (11), we obtain
$c = 2/(4-2^\alpha)$
as in Equation (11), we obtain
for all
![]() $\delta>0$
sufficiently small. The proof is concluded by noting that
$\delta>0$
sufficiently small. The proof is concluded by noting that
![]() $p(\delta) \to \mathbb{P} \left\{ B_\alpha(\!-\!1)<0, B_\alpha(1)<0 \right \} > 0$
and
$p(\delta) \to \mathbb{P} \left\{ B_\alpha(\!-\!1)<0, B_\alpha(1)<0 \right \} > 0$
and
![]() $\delta^{\alpha/2}q(\delta,\lambda)^{-1} = O(1)$
, by Lemma 4.
$\delta^{\alpha/2}q(\delta,\lambda)^{-1} = O(1)$
, by Lemma 4.
Proof of Lemma 6. After some algebraic transformations, from (12) we find that
Let
![]() $f(x) = 2x^{\alpha}-(x-1)^\alpha-(x+1)^\alpha$
. For
$f(x) = 2x^{\alpha}-(x-1)^\alpha-(x+1)^\alpha$
. For
![]() $x>1$
we have
$x>1$
we have
 \begin{align*}f'(x) &= \alpha x^{\alpha-1}\left(2-(1-1/x)^{\alpha-1}-(1+1/x)^{\alpha-1} \right)\\[5pt] &=\alpha x^{\alpha-1}\left[ 2 - \sum_{n=0}^\infty (\!-\!1)^n \frac{(\alpha-1)\cdots(\alpha-n)}{n!}x^{-n} - \sum_{n=0}^\infty \frac{(\alpha-1)\cdots(\alpha-n)}{n!}x^{-n}\right]\\[5pt] &=\alpha x^{\alpha-3}(\alpha-1)(2-\alpha)\left[\frac{1}{2!} + \sum_{n=1}^\infty \frac{(\alpha-3)\cdots(\alpha-2(n+1))}{(2(n+1))!}x^{-2n}\right]. \end{align*}
\begin{align*}f'(x) &= \alpha x^{\alpha-1}\left(2-(1-1/x)^{\alpha-1}-(1+1/x)^{\alpha-1} \right)\\[5pt] &=\alpha x^{\alpha-1}\left[ 2 - \sum_{n=0}^\infty (\!-\!1)^n \frac{(\alpha-1)\cdots(\alpha-n)}{n!}x^{-n} - \sum_{n=0}^\infty \frac{(\alpha-1)\cdots(\alpha-n)}{n!}x^{-n}\right]\\[5pt] &=\alpha x^{\alpha-3}(\alpha-1)(2-\alpha)\left[\frac{1}{2!} + \sum_{n=1}^\infty \frac{(\alpha-3)\cdots(\alpha-2(n+1))}{(2(n+1))!}x^{-2n}\right]. \end{align*}
We see that each of the terms in the sum above is positive, so
![]() $\textrm{sgn}(f'(x)) = \textrm{sgn}(\alpha-1)$
. Thus, f’(x) is negative for
$\textrm{sgn}(f'(x)) = \textrm{sgn}(\alpha-1)$
. Thus, f’(x) is negative for
![]() $\alpha\in (0,1)$
and positive for
$\alpha\in (0,1)$
and positive for
![]() $\alpha\in(1,2)$
. Finally, since
$\alpha\in(1,2)$
. Finally, since
and
![]() $c^-(1) + c^+(1) =1$
, the claim follows.
$c^-(1) + c^+(1) =1$
, the claim follows.
Proof of Lemma
8. It is sufficient to show that for any
![]() $\eta>0$
,
$\eta>0$
,
 \begin{eqnarray*}\frac{\partial}{\partial \eta}\left(\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\right) =\sum_{k=1}^\infty\frac{\partial}{\partial \eta}\left(\frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\right). \end{eqnarray*}
\begin{eqnarray*}\frac{\partial}{\partial \eta}\left(\sum_{k=1}^\infty \frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\right) =\sum_{k=1}^\infty\frac{\partial}{\partial \eta}\left(\frac{\Psi\left(\sqrt{\frac{\eta k}{2}}\right)}{k}\right). \end{eqnarray*}
Take
![]() $a,b>0$
such that
$a,b>0$
such that
![]() $\eta\in [a,b]$
,
$\eta\in [a,b]$
,
![]() $f(\eta) = \sum_{k=1}^\infty (\Psi(\sqrt{\eta k/2})/k)$
and
$f(\eta) = \sum_{k=1}^\infty (\Psi(\sqrt{\eta k/2})/k)$
and
![]() $f_n(\eta) =\sum_{k=1}^n (\Psi(\sqrt{\eta k/2})/k)$
,
$f_n(\eta) =\sum_{k=1}^n (\Psi(\sqrt{\eta k/2})/k)$
,
![]() $n \in \mathbb{N}$
. According to [Reference Kudryavtsev, Kutasov, Chehlov and Shabunin30, paragraph 3.1, p. 385], to claim the line above it is enough to show that (1) there exists
$n \in \mathbb{N}$
. According to [Reference Kudryavtsev, Kutasov, Chehlov and Shabunin30, paragraph 3.1, p. 385], to claim the line above it is enough to show that (1) there exists
![]() $\eta_0 \in[a,b]$
such that the sequence
$\eta_0 \in[a,b]$
such that the sequence
![]() $\{f_n(\eta_0)\}_{n\in \mathbb{N}}$
converges to a finite limit, and (2)
$\{f_n(\eta_0)\}_{n\in \mathbb{N}}$
converges to a finite limit, and (2)
![]() $f'_n(\eta)$
,
$f'_n(\eta)$
,
![]() $\eta\in [a,b]$
, converge uniformly to some function.
$\eta\in [a,b]$
, converge uniformly to some function.
The first condition holds since
![]() $\Psi(x)<e^{-x^2/2}$
for
$\Psi(x)<e^{-x^2/2}$
for
![]() $x>0$
. For the second condition we need to prove that, uniformly for all
$x>0$
. For the second condition we need to prove that, uniformly for all
![]() $\eta\in [a,b]$
, it holds that
$\eta\in [a,b]$
, it holds that
![]() $\sum_{k=n+1}^\infty f'_k(\eta) \to 0$
as
$\sum_{k=n+1}^\infty f'_k(\eta) \to 0$
as
![]() $n \to \infty$
. We have
$n \to \infty$
. We have
so the claim holds.
Acknowledgements
We would like to thank Professor Enkelejd Hashorva and Professor Krzysztof Dębicki for fruitful discussions.
Funding information
K. Bisewski’s research was funded by SNSF Grant 200021-196888. G. Jasnovidov was supported by the Ministry of Science and Higher Education of the Russian Federation, under agreements 075-15-2019-1620 (dated 08/11/2019) and 075-15-2022-289 (dated 06/04/2022).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.