On the rate of convergence for an α-stable central limit theorem under sublinear expectation

Abstract

We propose a monotone approximation scheme for a class of fully nonlinear degenerate partial integro-differential equations which characterize nonlinear $\alpha$-stable Lévy processes under a sublinear expectation space with $\alpha\in(1,2)$. We further establish the error bounds for the monotone approximation scheme. This in turn yields an explicit Berry–Esseen bound and convergence rate for the $\alpha$-stable central limit theorem under sublinear expectation.

1. Introduction

Motivated by measuring risks under model uncertainty, [31–33, 36] introduced the notion of a sublinear expectation space, called a G-expectation space. The G-expectation theory has been widely used to evaluate random outcomes, not using a single probability measure, but using the supremum over a family of possibly mutually singular probability measures. One of the fundamental results in this theory is the robust central limit theorem introduced in [34, 36]. The corresponding convergence rate was an open problem until recently. The first convergence rate was established in [14, 37] using Stein’s method and later in [28] using a stochastic control method under different model assumptions. More recently, [20] studied the convergence rate of a more general central limit theorem via a monotone approximation scheme for the G-equation.

On the other hand, nonlinear Lévy processes have been studied in [19, 29]. For $\alpha\in(1,2)$ , they considered a nonlinear $\alpha$ -stable Lévy process $(X_{t})_{t\geq0}$ defined on a sublinear expectation space $(\Omega,\mathcal{H},\hat{\mathbb{E}})$ , whose local characteristics are described by a set of Lévy triplets $\Theta=\{(0,0,F_{k_{\pm}})\colon k_{\pm}\in K_{\pm}\}$ , where $K_{\pm}\subset(\lambda_{1},\lambda_{2})$ for some $\lambda_{1},\lambda_{2}\geq0$ , and $F_{k_{\pm}}(\textrm{d} z)$ is the $\alpha$ -stable Lévy measure

\[ F_{k_{\pm}}(\textrm{d} z) = \frac{k_{-}}{|z|^{\alpha+1}}\mathbf{1}_{(\!-\infty,0)}(z)\,\textrm{d} z + \frac{k_{+}}{|z|^{\alpha+1}}\mathbf{1}_{(0,+\infty)}(z)\,\textrm{d} z.\]

Such a nonlinear $\alpha$ -stable Lévy process can be characterized via a fully nonlinear partial integro-differential equation (PIDE). For any $\phi \in C_{\textrm{b,Lip}}(\mathbb{R})$ , [29] proved the representation result $u(t,x)\;:\!=\;\hat{\mathbb{E}}[\phi(x+X_{t})]$ , $(t,x)\in \lbrack 0,T]\times \mathbb{R}$ , where u is the unique viscosity solution of the fully nonlinear PIDE

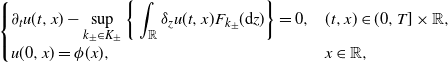(1) \begin{equation} \left \{ \begin{array}[c]{l@{\quad}l} \displaystyle \partial_{t}u(t,x) - \sup\limits_{k_{\pm}\in K_{\pm}} \bigg\{\int_{\mathbb{R}}\delta_{z}u(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} = 0, & (t,x)\in(0,T]\times\mathbb{R}, \\[5pt] \displaystyle u(0,x)=\phi(x), & x\in \mathbb{R}, \end{array} \right. \end{equation}

with $\delta_{z}u(t,x)\;:\!=\;u(t,x+z)-u(t,x)-D_{x}u(t,x)z$ . In contrast to the fully nonlinear PIDEs studied in the partial differential equation (PDE) literature, (1) is driven by a family of $\alpha$ -stable Lévy measures rather than a single Lévy measure. Moreover, since $F_{k_{\pm}}(\textrm{d} z)$ possesses a singularity at the origin, the integral term degenerates and (1) is a degenerate equation.

The corresponding generalized central limit theorem for $\alpha$ -stable random variables under sublinear expectation was established in [6]. For this, let $(\xi_{i})_{i=1}^{\infty}$ be a sequence of independent and identically distributed (i.i.d.) $\mathbb{R}$ -valued random variables on a sublinear expectation space $(\Omega,\mathcal{H},\tilde{\mathbb{E})}$ . After proper normalization, [6] showed that

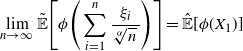\[ \lim_{n\rightarrow\infty}\tilde{\mathbb{E}}\Bigg[\phi\Bigg(\sum_{i=1}^{n} \frac{\xi_{i}}{\sqrt[\alpha]{n}\,}\Bigg)\Bigg] = {\hat{\mathbb{E}}}[\phi(X_{1})]\]

for any $\phi\in C_{\textrm{b,Lip}}(\mathbb{R})$ . We refer to the above convergence result as the $\alpha$ -stable central limit theorem under sublinear expectation.

Noting that $\hat{\mathbb{E}}[\phi(X_{1})]=u(1,0)$ , where u is the viscosity solution of (1), in this work we study the rate of convergence for the $\alpha$ -stable central limit theorem under sublinear expectation via the numerical analysis method for the nonlinear PIDE (1). To do this, we first construct a sublinear expectation space $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ and introduce a random variable $\xi$ on this space. For given $T>0$ and $\Delta \in(0,1)$ , using the random variable $\xi$ under $\tilde{\mathbb{E}}$ as input, we define a discrete scheme $u_{\Delta}\colon[0,T]\times \mathbb{R\rightarrow R}$ to approximate u by

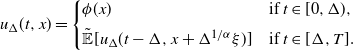(2) \begin{equation} u_{\Delta}(t,x) = \left\{ \begin{array}[c]{l@{\quad}l} \phi(x) & \text{if } t\in\lbrack0,\Delta), \\[5pt] \tilde{\mathbb{E}}[u_{\Delta}(t-\Delta,x+\Delta^{1/\alpha}\xi)] & \text{if } t\in \lbrack \Delta,T]. \end{array} \right. \end{equation}

Taking $T=1$ and $\Delta={1}/{n}$ , we can recursively apply the above scheme to obtain

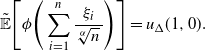\[ \tilde{\mathbb{E}}\Bigg[\phi\Bigg(\sum_{i=1}^{n}\frac{\xi_{i}}{\sqrt[\alpha]{n}\,}\Bigg)\Bigg]=u_{\Delta}(1,0).\]

In this way, the convergence rate of the $\alpha$ -stable central limit theorem is transformed into the convergence rate of the discrete scheme (2) for approximating the nonlinear PIDE (1).

The basic framework for convergence of numerical schemes to viscosity solutions of Hamilton–Jacobi–Bellman equations was established in [5], which showed that any monotone, stable, and consistent approximation scheme converges to the correct solution, provided that there exists a comparison principle for the limiting equation. The corresponding convergence rate was first obtained with the introduction of the shaking coefficients technique to construct a sequence of smooth subsolutions/supersolutions in [25–27]. This technique was further developed to general monotone approximation schemes (see [2–4] and references therein).

The design and analysis of numerical schemes for nonlinear PIDEs is a relatively new area of research. For nonlinear degenerate PIDEs driven by a family of $\alpha$ -stable Lévy measures, there are no general results giving error bounds for numerical schemes. Most of the existing results in the PDE literature only deal with a single Lévy measure and its finite difference method, e.g. [7–9, 22]. One exception is [12], which considers a nonlinear PIDE driven by a set of tempered $\alpha$ -stable Lévy measures for $\alpha \in(0,1)$ by using the finite difference method.

To derive the error bounds for the discrete scheme (2), the key step is to interchange the roles of the discrete scheme and the original equation when the approximate solution has enough regularity. The classical regularity estimates of the approximate solution depend on the finite variance of random variables. Since $\xi$ has infinite variance, the method developed in [28] cannot be applied to $u_{\Delta}$ . To overcome this difficulty, by introducing a truncated discrete scheme $u_{\Delta,N}$ related to a truncated random variable $\xi^{N}$ with finite variance, we construct a new type of regularity estimate of $u_{\Delta,N}$ that plays a pivotal role in establishing the space and time regularity properties for $u_{\Delta}$ . With the help of a precise estimate of the truncation $\tilde{\mathbb{E}}[|\xi-\xi^{N}|]$ , a novel estimate for $|u_{\Delta}-u_{\Delta,N}|$ is obtained. By choosing a proper N, we then establish the regularity estimates for $u_{\Delta}$ . Together with the concavity of (1) and (2), and the regularity estimates of their solutions, we are able to interchange their roles and thus derive the error bounds for the discrete scheme. To the best of our knowledge, these are the first error bounds for numerical schemes for fully nonlinear PIDEs associated with a family of $\alpha$ -stable Lévy measures, which in turn provide a nontrivial convergence rate result for the $\alpha$ -stable central limit theorem under sublinear expectation.

On the other hand, the classical probability literature mainly deals with $\Theta$ as a singleton, so $(X_{t})_{t\geq0}$ becomes a classical Lévy process with triplet $\Theta$ , and $X_{1}$ is an $\alpha$ -stable random variable. The corresponding convergence rate of the classical $\alpha$ -stable central limit theorem (with $\Theta$ as a singleton) has been studied using the Kolmogorov distance (see, e.g., [13, 15–17, 21, 24]) and the Wasserstein-1 distance or the smooth Wasserstein distance (see, e.g., [1, 10, 11, 23, 30, 38]). The first type is proved by the characteristic functions, which do not exist in the sublinear framework, while the second type relies on Stein’s method which also fails under the sublinear setting.

The rest of the paper is organized as follows. In Section 2, we review some necessary results about sublinear expectation and $\alpha$ -stable Lévy processes. In Section 3, we list the assumptions and our main results, the convergence rate of $\alpha$ -stable random variables under sublinear expectation. We present two examples to illustrate our results in Section 4. Finally, by using the monotone scheme method, the proof of our main result is given in Section 5.

2. Preliminaries

In this section, we recall some basic results of sublinear expectation and $\alpha$ -stable Lévy processes that are needed in the sequel. For more details, we refer the reader to [6, 29, 32, 36] and the references therein.

We start with some notation. Let $C_\textrm{Lip}(\mathbb{R}^{n})$ be the space of Lipschitz functions on $\mathbb{R}^{n}$ , and $C_\textrm{b,Lip}(\mathbb{R}^{n})$ be the space of bounded Lipschitz functions on $\mathbb{R}^{n}$ . For any subset $Q\subset \lbrack0,T]\times \mathbb{R}$ and for any bounded function on Q, we define the norm $|\omega|_{0}\;:\!=\;\sup_{(t,x)\in Q}|\omega(t,x)|$ . We also use the following spaces: $C_\textrm{b}(Q)$ and $C_\textrm{b}^{\infty}(Q)$ , denoting, respectively, the space of bounded continuous functions on Q and the space of bounded continuous functions on Q with bounded derivatives of any order. For the rest of this paper we take a nonnegative function $\zeta \in C^{\infty} (\mathbb{R}^{2})$ with unit integral and support in $\{(t,x)\colon-1<t<0,|x|<1\}$ and, for $\varepsilon \in(0,1)$ , let $\zeta_{\varepsilon}(t,x)=\varepsilon^{-3}\zeta(t/\varepsilon^{2},x/\varepsilon)$ .

2.1. Sublinear expectation

Let $\mathcal{H}$ be a linear space of real-valued functions defined on a set $\Omega$ such that if $X_{1},\ldots,X_{n}\in\mathcal{H}$ , then $\varphi(X_{1},\ldots,X_{n})\in \mathcal{H}$ for each $\varphi \in C_{\textrm{Lip}}(\mathbb{R}^{n})$ .

Definition 1. A functional $\hat{\mathbb{E}}\colon\mathcal{H}\rightarrow\mathbb{R}$ is called a sublinear expectation if, for all $X,Y \in \mathcal{H}$ , it satisfies the following properties:

1. (i) Monotonicity: If $X\geq Y$ then $\hat{\mathbb{E}}[X] \geq \hat{\mathbb{E}}[Y]$ .

2. (ii) Constant preservation: $\hat{\mathbb{E}}[c]=c$ for any $c\in \mathbb{R}$ .

3. (iii) Subadditivity: $\hat{\mathbb{E}}[X+Y] \leq \hat{\mathbb{E}}[X] + \hat{\mathbb{E}}[Y]$ .

4. (iv) Positive homogeneity: $\hat{\mathbb{E}}[\lambda X] = \lambda\hat{\mathbb{E}}[X]$ for each $\lambda>0$ .

The triplet $(\Omega,\mathcal{H},\hat{\mathbb{E})}$ is called a sublinear expectation space. From the definition of the sublinear expectation $\hat{\mathbb{E}}$ , the following results can be easily obtained.

Proposition 1. For $X,Y \in \mathcal{H}$ ,

1. (i) if $\hat{\mathbb{E}}[X] = -\hat{\mathbb{E}}[-X]$ , then $\hat{\mathbb{E}}[X+Y] = \hat{\mathbb{E}}[X] + \hat{\mathbb{E}}[Y]$ ;

2. (ii) $|\hat{\mathbb{E}}[X] - \hat{\mathbb{E}}[Y]| \leq \hat{\mathbb{E}}[\vert X-Y\vert]$ ;

3. (iii) $\hat{\mathbb{E}}[\vert XY\vert] \leq (\hat{\mathbb{E}}[\vert X\vert^{p}])^{1/p} \cdot (\hat{\mathbb{E}}[\vert Y\vert^{q}])^{1/q}$ for $1\leq p,q<\infty$ with ${1}/{p}+{1}/{q}=1$ .

Definition 2. Let $X_{1}$ and $X_{2}$ be two n-dimensional random vectors defined respectively in sublinear expectation spaces $(\Omega_{1},\mathcal{H}_{1},\hat{\mathbb{E}}_{1})$ and $(\Omega_{2},\mathcal{H}_{2},\hat{\mathbb{E}}_{2})$ . They are called identically distributed, denoted by $X_{1}\overset{\textrm{d}}{=}X_{2}$ , if $\hat{\mathbb{E}}_{1}[\varphi(X_{1})] = \hat{\mathbb{E}}_{2}[\varphi(X_{2})]$ for all $\varphi \in C_\textrm{Lip}(\mathbb{R}^{n})$ .

Definition 3. In a sublinear expectation space $(\Omega,\mathcal{H},\hat{\mathbb{E})}$ , a random vector $Y=(Y_{1}$ , $\ldots,Y_{n}) \in \mathcal{H}^{n}$ is said to be independent of another random vector $X=(X_{1},\ldots,X_{m})\in\mathcal{H}^{m}$ under $\hat{\mathbb{E}}[\!\cdot\!]$ , denoted by $Y\perp X$ , if, for every test function $\varphi \in C_\textrm{Lip}(\mathbb{R}^{m}\times \mathbb{R}^{n})$ , $\hat{\mathbb{E}}[\varphi(X,Y)] = \hat{\mathbb{E}}[\hat{\mathbb{E}}[\varphi(x,Y)]_{x=X}]$ . $\bar{X}=(\bar{X}_{1},\ldots,\bar{X}_{m})\in \mathcal{H}^{m}$ is said to be an independent copy of X if $\bar{X}\overset{\textrm{d}}{=}X$ and $\bar{X}\perp X$ .

More details concerning general sublinear expectation spaces can be found in [33, 36] and references therein.

2.2. $\alpha$ -stable Lévy process

Definition 4. Let $\alpha\in(0,2]$ . A random variable X on a sublinear expectation space $(\Omega,\mathcal{H},\hat{\mathbb{E})}$ is said to be (strictly) $\alpha$ -stable if, for all $a,b\geq0$ , $aX+bY\overset{\textrm{d}}{=}(a^{\alpha}+b^{\alpha})^{1/\alpha}X$ , where Y is an independent copy of X.

Remark 1. For $\alpha=1$ , X is the maximal random variable discussed in [18, 34, 36]. When $\alpha=2$ , X becomes the G-normal random variable introduced in [35, 36]. In this paper, we shall focus on the case of $\alpha\in(1,2)$ and consider X for a nonlinear $\alpha$ -stable Lévy process $(X_{t})_{t\geq0}$ in the framework of [29].

Let $\alpha \in(1,2)$ , $K_{\pm}$ be a bounded measurable subset of $\mathbb{R}_{+}$ , and $F_{k_{\pm}}$ be the $\alpha$ -stable Lévy measure

\[ F_{k_{\pm}}(\textrm{d} z) = \frac{k_{-}}{|z|^{\alpha+1}}\mathbf{1}_{(\!-\infty,0)}(z)\,\textrm{d} z + \frac{k_{+}}{|z|^{\alpha+1}}\mathbf{1}_{(0,+\infty)}(z)\,\textrm{d} z\]

for all $k_{-},k_{+}\in K_{\pm}$ , and denote by $\Theta\;:\!=\;\{(0,0,F_{k_{\pm}})\colon k_{\pm}\in K_{\pm}\}$ the set of Lévy triplets. From [29, Theorem 2.1], we can define a nonlinear $\alpha$ -stable Lévy process $(X_{t})_{t\geq0}$ with respect to a sublinear expectation $\hat{\mathbb{E}}[\!\cdot\!] = \sup_{P\in\mathfrak{B}_{\Theta}}E^{P}[\!\cdot\!]$ , where $E^{P}$ is the usual expectation under the probability measure P, and $\mathfrak{B}_{\Theta}$ is the set of all semimartingales with $\Theta$ -valued differential characteristics. This implies the following:

• • $(X_{t})_{t\geq0}$ is real-valued càdlàg process and $X_{0}=0$ .

• • $(X_{t})_{t\geq0}$ has stationary increments, i.e. $X_{t}-X_{s}$ and $X_{t-s}$ are identically distributed for all $0\leq s\leq t$ .

• • $(X_{t})_{t\geq0}$ has independent increments, i.e. $X_{t}-X_{s}$ is independent of $(X_{s_{1}},\ldots,X_{s_{n}})$ for each $n\in\mathbb{N}$ and $0\leq s_{1}\leq \cdots \leq s_{n}\leq s$ .

We now present some basic lemmas for the $\alpha$ -stable Lévy process $(X_{t})_{t\geq0}$ . We refer to [6, Lemmas 2.6–2.9] and [29, Lemmas 5.1–5.3] for the details of the proofs.

Lemma 1. $\hat{\mathbb{E}}[|X_{1}|]<\infty$ .

Lemma 2. For all $\lambda>0$ and $t\geq0$ , $X_{\lambda t}$ and $\lambda^{1/\alpha}X_{t}$ are identically distributed.

Lemma 3. Suppose that $\phi\in C_\textrm{b,Lip}(\mathbb{R})$ . Then, for any $(t,x)\in[0,T]\times\mathbb{R}$ , $u(t,x)=\hat{\mathbb{E}}[\phi(x+X_{t})]$ is the unique viscosity solution of the fully nonlinear PIDE

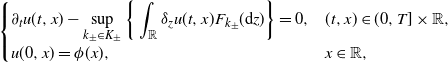(3) \begin{equation} \left \{ \begin{array}[c]{l@{\quad}l} \displaystyle \partial_{t}u(t,x) - \sup\limits_{k_{\pm}\in K_{\pm}} \bigg\{\int_{\mathbb{R}}\delta_{z}u(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} = 0, & (t,x) \in (0,T]\times\mathbb{R}, \\[5pt] \displaystyle u(0,x) = \phi(x), & x \in \mathbb{R}, \end{array} \right. \end{equation}

with $\delta_{z}u(t,x)\;:\!=\;u(t,x+z)-u(t,x)-D_{x}u(t,x)z$ . Moreover, for any $0\leq s\leq t\leq T$ , $u(t,x)=\hat{\mathbb{E}}[u(t-s,x+X_{s})]$ .

Lemma 4. Suppose that $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ . Then the function u is uniformly bounded by $|\phi|_{0}$ and jointly continuous. More precisely, for any $t,s\in[0,T]$ and $x,y\in\mathbb{R}$ ,

\[ \vert u(t,x) - u(s,y)\vert \leq C_{\phi,\mathcal{K}}(|x-y|+|t-s|^{1/\alpha}), \]

where $C_{\phi,\mathcal{K}}$ is a constant depending only on the Lipschitz constant of $\phi$ and

\[ \mathcal{K} \;:\!=\; \sup\limits_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{\mathbb{R}}|z|\wedge|z|^{2}F_{k_{\pm}}(\textrm{d} z)\bigg\} < \infty. \]

3. Main results

First, we construct a sublinear expectation space and introduce random variables on it. For each $k_{\pm}\in K_{\pm}\subset(\lambda_{1},\lambda_{2})$ for some $\lambda_{1},\lambda_{2}\geq0$ , let $W_{k_{\pm}}$ be a classical mean-zero random variable with a cumulative distribution function (CDF)

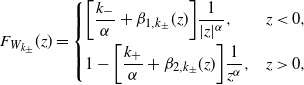(4) \begin{equation} F_{W_{k_{\pm}}}(z) = \left \{ \begin{array}[c]{l@{\quad}l} \displaystyle \bigg[\frac{k_{-}}{\alpha} + \beta_{1,k_{\pm}}(z)\bigg]\frac{1}{|z|^{\alpha}}, & z<0, \\[3mm] \displaystyle 1 - \bigg[\frac{k_{+}}{\alpha} + \beta_{2,k_{\pm}}(z)\bigg]\frac{1}{z^{\alpha}}, & z>0, \end{array} \right. \end{equation}

for some functions $\beta_{1,k_{\pm}}\colon(\!-\infty,0] \rightarrow \mathbb{R}$ and $\beta_{2,k_{\pm}}\colon[0,\infty)\rightarrow \mathbb{R}$ such that $\lim_{z\rightarrow-\infty}\beta_{1,k_{\pm}}(z)=\lim_{z\rightarrow \infty}\beta_{2,k_{\pm}}(z)=0$ . Define a sublinear expectation $\tilde{\mathbb{E}}$ on $C_\textrm{Lip}(\mathbb{R})$ by

\begin{equation*} \tilde{\mathbb{E}}[\varphi] = \sup_{k_{\pm}\in K_{\pm}} \int_{\mathbb{R}}\varphi(z)\,\textrm{d} F_{W_{k_{\pm}}}(z)\end{equation*}

for all $\varphi \in C_\textrm{Lip}(\mathbb{R})$ . Clearly, $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ is a sublinear expectation space. Let $\xi$ be a random variable on this space given by $\xi(z)=z$ for all $z\in \mathbb{R}$ . Since $W_{k\pm}$ has mean zero, this yields $\tilde{\mathbb{E}}[\xi]=\tilde{\mathbb{E}}[-\xi]=0$ .

We need the following assumptions, which are motivated by [6, Example 4.2].

Assumption 1. For each $k_{\pm}\in K_{\pm}$ , $\beta_{1,k_{\pm}}$ and $\beta_{2,k_{\pm}}$ are continuously differentiable functions in (4) satisfying $\int_{\mathbb{R}}z\,\textrm{d} F_{W_{k_{\pm}}}(z)=0$ .

Assumption 2. There exists a constant $M>0$ such that, for any $k_{\pm}\in K_{\pm}$ , the following quantities are less than M:

\[ \bigg\vert\int_{-\infty}^{-1}\frac{\beta_{1,k_{\pm}}(z)}{|z|^{\alpha}}\,\textrm{d} z\bigg\vert, \qquad \bigg\vert\int_{1}^{\infty}\frac{\beta_{2,k_{\pm}}(z)}{z^{\alpha}}\,\textrm{d} z\bigg\vert .\]

Assumption 3. There exists a constant $q>0$ such that, for any $k_{\pm}\in K_{\pm}$ and $\Delta \in(0,1)$ , the following quantities are less than $C\Delta^{q}$ :

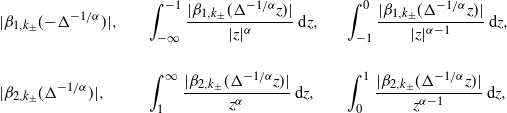$$\begin{array}[c]{l@{\quad}l@{\quad}l} \displaystyle|\beta_{1,k_{\pm}}(\!-\!\Delta^{-1/\alpha})|,& \displaystyle\int_{-\infty}^{-1}\frac{|\beta_{1,k_{\pm}}(\Delta^{-1/\alpha}z)|}{|z|^{\alpha}}\,\textrm{d} z, & \displaystyle\int_{-1}^{0}\frac{|\beta_{1,k_{\pm}}(\Delta^{-1/\alpha}z)|}{|z|^{\alpha-1}}\,\textrm{d} z, \\[5pt] & & \\[5pt] \displaystyle|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha})|, & \displaystyle\int_{1}^{\infty}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha}}\,\textrm{d} z, & \displaystyle\int_{0}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z, \end{array} $$

where $C>0$ is a constant.

Remark 2. Note that by Assumption 1 alone, the terms in Assumption 2 are finite and the terms in Assumption 3 approach zero as $\Delta\rightarrow0$ . In other words, the content of Assumptions 2 and 3 are the uniform bounds and the existence of minimum convergence rates.

Remark 3. By (4), we can write $\beta_{1,k_{\pm}}$ and $\beta_{2,k_{\pm}}$ as

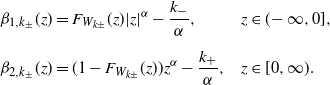\begin{alignat*}{2} \beta_{1,k_{\pm}}(z) & = F_{W_{k\pm}}(z)|z|^{\alpha} - \frac{k_{-}}{\alpha}, & z & \in (\!-\infty,0], \\[5pt] \beta_{2,k_{\pm}}(z) & = (1-F_{W_{k\pm}}(z))z^{\alpha} - \frac{k_{+}}{\alpha}, \quad & z & \in \lbrack0,\infty). \end{alignat*}

Under Assumption 1, it can be checked that for any $k_{\pm}\in K_{\pm}$ the following quantities are uniformly bounded (we also assume the uniform bound is M):

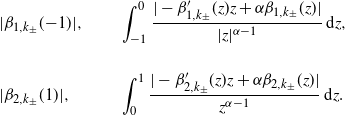\[ \begin{array}[c]{l@{\quad}l@{\quad}l} \displaystyle|\beta_{1,k_{\pm}}(\!-\!1)|, & & \displaystyle\int_{-1}^{0}\frac{|-\beta_{1,k_{\pm}}^{\prime}(z)z+\alpha\beta_{1,k_{\pm}}(z)|} {|z|^{\alpha-1}}\,\textrm{d} z, \\[5pt] & & \\[5pt] \displaystyle|\beta_{2,k_{\pm}}(1)|, & & \displaystyle\int_{0}^{1}\frac{|-\beta_{2,k_{\pm}}^{\prime}(z)z+\alpha\beta_{2,k_{\pm}}(z)|}{z^{\alpha-1}}\,\textrm{d} z. \end{array} \]

Remark 4. Under Assumptions 1 and (A2), it is easy to check that

\[ \tilde{\mathbb{E}}[|\xi|] = \tilde{\mathbb{E}}\bigg[\int_{0}^{\infty}\mathbf{1}_{\{|\xi|>z\}}\,\textrm{d} z\bigg] = \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{0}^{\infty}P_{k_{\pm}}(|\xi|>z)\,\textrm{d} z\bigg\} , \]

where $\{P_{k_{\pm}}, k_{\pm}\in K_{\pm}\}$ is the set of probability measures related to uncertainty distributions $\{F_{W_{k\pm}},k_{\pm}\in K_{\pm}\}$ . It follows that

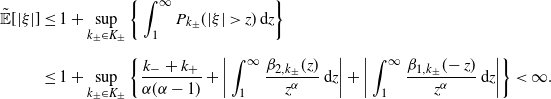\begin{align*} \tilde{\mathbb{E}}[|\xi|] & \leq 1 + \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{1}^{\infty}P_{k_{\pm}}(|\xi|>z)\,\textrm{d} z\bigg\} \\[5pt] & \leq 1 + \sup_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{\alpha(\alpha-1)} + \bigg\vert\int_{1}^{\infty}\frac{\beta_{2,k_{\pm}}(z)}{z^{\alpha}}\,\textrm{d} z\bigg\vert + \bigg\vert\int_{1}^{\infty}\frac{\beta_{1,k_{\pm}}(\!-z)}{z^{\alpha}}\,\textrm{d} z\bigg\vert\bigg\} < \infty. \end{align*}

Similarly,

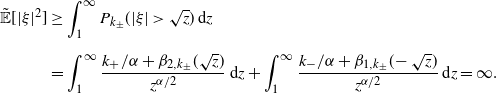\begin{align*} \tilde{\mathbb{E}}[|\xi|^{2}] & \geq \int_{1}^{\infty}P_{k_{\pm}}(|\xi|>\sqrt{z})\,\textrm{d} z \\[5pt] & = \int_{1}^{\infty}\frac{k_{+}/\alpha+\beta_{2,k_{\pm}}(\sqrt{z})}{z^{\alpha/2}}\,\textrm{d} z + \int_{1}^{\infty}\frac{k_{-}/\alpha+\beta_{1,k_{\pm}}(\!-\sqrt{z})}{z^{\alpha/2}}\,\textrm{d} z = \infty. \end{align*}

Let $(\xi_{i})_{i=1}^{\infty}$ be a sequence of i.i.d. $\mathbb{R}$ -valued random variables defined on $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ in the sense that $\xi_{1}=\xi$ , $\xi_{i+1}\overset{\textrm{d}}{=}\xi_{i}$ , and $\xi_{i+1}\perp(\xi_{1},\xi_{2},\ldots,\xi_{i})$ for each $i\in \mathbb{N}$ ; we write

(5) \begin{equation}\bar{S}_{n}\;:\!=\;\sum_{i=1}^{n}\frac{\xi_{i}}{\sqrt[\alpha]{n}\,}. \end{equation}

Now we state our first main result.

Theorem 1. Suppose that Assumptions 1–3 hold. Let $(\bar{S}_{n})_{n=1}^{\infty}$ be a sequence as defined in (5), and $(X_{t})_{t\geq0}$ be a nonlinear $\alpha$ -stable Lévy process with the characteristic set $\Theta$ . Then, for any $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ , $\big|\tilde{\mathbb{E}}[\phi(\bar{S}_{n})] - \hat{\mathbb{E}}[\phi(X_{1})]\big| \leq C_{0}n^{-\Gamma(\alpha,q)}$ , where

\begin{equation*}\Gamma(\alpha,q) = \min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha},\frac{q}{2}\bigg\}\end{equation*}

with $q>0$ given in Assumption 3, and $C_{0}$ is a constant depending on the Lipschitz constant of $\phi$ , which is given in Theorem 2.

Remark 5. The classical $\alpha$ -stable central limit theorem (see, e.g., [21, Theorem 2.6.7]) states that for a classical mean-zero random variable $\xi_{1}$ , the sequence $\bar{S}_{n}$ converges in law to $X_{1}$ as $n\rightarrow \infty$ if and only if the CDF of $\xi$ has the form given in (4), where $(X_{t})_{t\geq0}$ is a classical Lévy process with triplet $(0,0,F_{k_{\pm}})$ . In the framework of sublinear expectation, sufficient conditions for the $\alpha$ -stable central limit theorem are given in [6], which showed that, for a mean-zero random variable $\xi_{1}$ under the sublinear expectation $\tilde{\mathbb{E}}$ defined above, $\bar{S}_{n}$ converges in law to $X_{1}$ as $n\rightarrow\infty$ , where $(X_{t})_{t\geq0}$ is a nonlinear Lévy process with triplet set $\Theta$ . Here, Theorem 1 further provides an explicit convergence rate of the limit theorem in [6], which can be seen as a special $\alpha$ -stable central limit theorem under the sublinear expectation.

Remark 6. Assumptions 1–3 are sufficient conditions for [6, Theorem 3.1]. Indeed, by [6, Proposition 2.10], we know that for any $0<h<1$ , $u\in C_\textrm{b}^{1,2}([h,1+h]\times\mathbb{R})$ . Under Assumptions 1–3, by using II from (19) we get, for any $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ and $0<h<1$ ,

\begin{equation*} n\bigg\vert\tilde{\mathbb{E}}\big[\delta_{n^{-1/\alpha}\xi_{1}}v(t,x)\big] - \frac{1}{n}\sup\limits_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}\delta_{z}v(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\}\bigg\vert \rightarrow 0 \end{equation*}

uniformly on $[0,1]\times \mathbb{R}$ as $n\rightarrow \infty$ , where v is the unique viscosity solution of

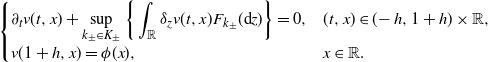\[ \left\{ \begin{array}[c]{l@{\quad}l} \displaystyle \partial_{t}v(t,x) + \sup\limits_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{\mathbb{R}}\delta_{z}v(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} = 0, & (t,x) \in (\!-h,1+h)\times\mathbb{R}, \\[5pt] \displaystyle v(1+h,x) = \phi(x), & x\in\mathbb{R}. \end{array} \right. \]

In addition, the necessary conditions for the $\alpha$ -stable central limit theorem under sublinear expectation are still unknown.

4. Two examples

In this section we give two examples to illustrate our results.

Example 1. Let $(\xi_{i})_{i=1}^{\infty}$ be a sequence of i.i.d. $\mathbb{R}$ -valued random variables defined on $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ with CDF (4) satisfying $\beta_{1,k_{\pm}}(z)=0$ for $z\leq-1$ and $\beta_{2,k_{\pm}}(z)=0$ for $z\geq1$ with $\lambda_{2}<{\alpha}/{2}$ . The exact expressions for $\beta_{1,k_{\pm}}(z)$ and $\beta_{2,k_{\pm}}(z)$ for $0<|z|<1$ are not specified here, but we require $\beta_{1,k_{\pm}}(z)$ and $\beta_{2,k_{\pm}}(z)$ to satisfy Assumption 1. It is clear that Assumption 2 holds. In addition, for each $k_{\pm}\in K_{\pm}$ and $\Delta\in(0,1)$ ,

\[ \int_{0}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z = \int_{0}^{\Delta^{1/\alpha}}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z \leq \frac{c}{2-\alpha}\Delta^{({2-\alpha})/{\alpha}}, \]

where $c\;:\!=\;\sup_{z\in(0,1)}|\beta_{2,k_{\pm}}(z)|<\infty$ , and similarly for the negative half-line. This indicates that Assumption 3 holds with $q=({2-\alpha})/{\alpha}$ . According to Theorem 1, we get the convergence rate $\big|\tilde{\mathbb{E}}[\phi(\bar{S}_{n})]-\hat{\mathbb{E}}[\phi(X_{1})]\big|\leq C_{0}n^{-\Gamma(\alpha)}$ , where

\begin{equation*}\Gamma(\alpha) = \min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha}\bigg\}.\end{equation*}

Example 2. Let $(\xi_{i})_{i=1}^{\infty}$ be a sequence of i.i.d. $\mathbb{R}$ -valued random variables defined on $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ with CDF (4) satisfying $\beta_{1,k_{\pm}}(z)=a_{1}|z|^{\alpha-\beta}$ for $z\leq-1$ and $\beta_{2,k_{\pm}}(z)= a_{2}z^{\alpha-\beta}$ for $z\geq1$ , with $\beta>\alpha$ and two proper constants $a_{1}, a_{2}$ . The exact expressions for $\beta_{1,k_{\pm}}(z)$ and $\beta_{2,k_{\pm}}(z)$ for $0<|z|<1$ are not specified here, but we require that $\beta_{1,k_{\pm}}(z)$ and $\beta_{2,k_{\pm}}(z)$ satisfy Assumption 1. For simplicity, we will only check the integral along the positive half-line; the negative half-line case is similar. Observe that

\[ \int_{1}^{\infty}\frac{\beta_{2,k_{\pm}}(z)}{z^{\alpha}}\,\textrm{d} z = \frac{a_{2}}{\beta-1}, \]

which shows that Assumption 2 holds. Also, it can be verified that, for each $k_{\pm}\in K_{\pm}$ and $\Delta \in(0,1)$ ,

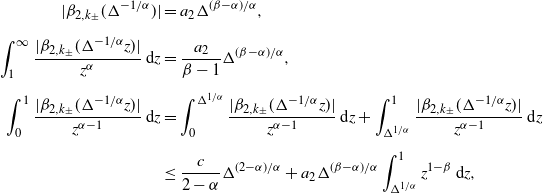\begin{align*} |\beta_{2,k_{\pm}}(\Delta^{-1/\alpha})| & = a_{2}\Delta^{({\beta-\alpha})/{\alpha}}, \\[5pt] \int_{1}^{\infty}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha}}\,\textrm{d} z & = \frac{a_{2}}{\beta-1}\Delta^{({\beta-\alpha})/{\alpha}}, \\[5pt] \int_{0}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z & = \int_{0}^{\Delta^{1/\alpha}}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z + \int_{\Delta^{1/\alpha}}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z \\[5pt] & \leq \frac{c}{2-\alpha}\Delta^{({2-\alpha})/{\alpha}} + a_{2}\Delta^{({\beta-\alpha})/{\alpha}}\int_{\Delta^{1/\alpha}}^{1}z^{1-\beta}\,\textrm{d} z, \end{align*}

where $c=\sup_{z\in(0,1)}|\beta_{2,k_{\pm}}(z)|<\infty$ . We further distinguish three cases based on the value of $\beta$ .

If $\beta=2$ ,

\[ \int_{0}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z \leq \frac{c}{2-\alpha}\Delta^{({2-\alpha})/{\alpha}} + a_{2}\Delta^{({2-\alpha})/{\alpha}}\ln\Delta^{-{1}/{\alpha}} \leq C\Delta^{({2-\alpha})/{\alpha}-\varepsilon}, \]

where $C=({c}/({2-\alpha}))+a_{2}$ , for any small $\varepsilon>0$ .

If $\alpha<\beta<2$ ,

\[ \int_{0}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z \leq \frac{c}{2-\alpha}\Delta^{({2-\alpha})/{\alpha}} + \frac{a_{2}}{2-\beta}(\Delta^{({\beta-\alpha})/{\alpha}} - \Delta^{({2-\alpha})/{\alpha}}) \leq C\Delta^{({\beta-\alpha})/{\alpha}}, \]

where

\begin{equation*}C=\frac{c}{2-\alpha}+\frac{2a_{2}}{2-\beta}.\end{equation*}

If $\beta>2$ , it follows that

\[ \int_{0}^{1}\frac{|\beta_{2,k_{\pm}}(\Delta^{-1/\alpha}z)|}{z^{\alpha-1}}\,\textrm{d} z \leq \frac{c}{2-\alpha}\Delta^{({2-\alpha})/{\alpha}} + \frac{a_{2}}{\beta-2}(\Delta^{({2-\alpha})/{\alpha}} - \Delta^{({\beta-\alpha})/{\alpha}}) \leq C\Delta^{({2-\alpha})/{\alpha}}, \]

where

\begin{equation*}C=\frac{c}{2-\alpha}+\frac{2a_{2}}{\beta-2}.\end{equation*}

Then, Assumption 3 holds with

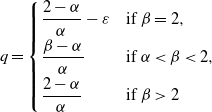\[ q=\left \{ \begin{array}[c]{l@{\quad}l} \dfrac{2-\alpha}{\alpha}-\varepsilon & \text{if }\beta=2, \\[2mm] \dfrac{\beta-\alpha}{\alpha} & \text{if }\alpha<\beta<2, \\[2mm] \dfrac{2-\alpha}{\alpha} & \text{if }\beta>2 \end{array} \right. \]

for any small $\varepsilon>0$ . From Theorem 1, we immediately obtain $\big|\tilde{\mathbb{E}}[\phi(\bar{S}_{n})]-\hat{\mathbb{E}}[\phi(X_{1})]\big|\leq C_{0}n^{-\Gamma(\alpha,\beta)}$ , where

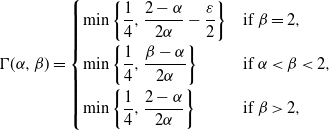\[ \Gamma(\alpha,\beta) = \left \{ \begin{array}[c]{l@{\quad}l} \min\bigg\{\dfrac{1}{4},\dfrac{2-\alpha}{2\alpha}-\dfrac{\varepsilon}{2}\bigg\} & \text{if }\beta=2, \\[3mm] \min\bigg\{\dfrac{1}{4},\dfrac{\beta-\alpha}{2\alpha}\bigg\} & \text{if }\alpha<\beta<2, \\[3mm] \min\bigg\{\dfrac{1}{4},\dfrac{2-\alpha}{2\alpha}\bigg\} & \text{if }\beta>2, \end{array} \right. \]

with $\varepsilon>0$ .

5. Proof of Theorem 1: Monotone scheme method

In this section we introduce the numerical analysis tools of nonlinear partial differential equations to prove Theorem 1. Noting that $\hat{\mathbb{E}}[\phi(X_{1})]=u(1,0)$ , where u is the viscosity solution of (3), we propose a discrete scheme to approximate u by merely using the random variable $\xi$ under $\tilde{\mathbb{E}}$ as input. For given $T>0$ and $\Delta \in(0,1)$ , define $u_{\Delta}\colon[0,T]\times \mathbb{R\rightarrow R}$ recursively by

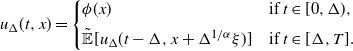(6) \begin{equation} u_{\Delta}(t,x) = \left\{ \begin{array}[c]{l@{\quad}l} \phi(x) & \text{if } t\in \lbrack0,\Delta), \\[5pt] \tilde{\mathbb{E}}[u_{\Delta}(t-\Delta,x+\Delta^{{1}/{\alpha}}\xi)] & \text{if } t\in\lbrack\Delta,T]. \end{array} \right.\end{equation}

From the above recursive process, we can see that, for each $x\in \mathbb{R}$ and $n\in \mathbb{N}$ such that $n\Delta \leq T$ , $u_{\Delta}(\cdot,x)$ is a constant on the interval $[n\Delta,(n+1)\Delta \wedge T)$ , that is, $u_{\Delta}(t,x)=u_{\Delta}(n\Delta,x)$ for all $t\in \lbrack n\Delta,(n+1)\Delta \wedge T)$ .

By induction (see [20, Theorem 2.1]), we can derive that, for all $n\in \mathbb{N}$ such that $n\Delta \leq T$ and $x\in \mathbb{R}$ ,

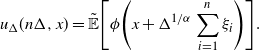\[ u_{\Delta}(n\Delta,x) = \tilde{\mathbb{E}}\Bigg[\phi\Bigg(x+\Delta^{{1}/{\alpha}}\sum_{i=1}^{n}\xi_{i}\Bigg)\Bigg].\]

In particular, taking $T=1$ and $\Delta={1}/{n}$ , we have $u_{\Delta}(1,0)=\tilde{\mathbb{E}[}\phi(\bar{S}_{n})]$ , and Theorem 1 follows from the following result.

Theorem 2. Suppose that Assumptions 1–3 hold, and $\phi\in C_\textrm{b,Lip}(\mathbb{R})$ . Then, for any $(t,x) \in \lbrack0,T]\times\mathbb{R}$ , $\vert u(t,x) - u_{\Delta}(t,x)\vert \leq C_{0}\Delta^{\Gamma(\alpha,q)}$ , where the Berry–Esseen constant $C_{0}=L_{0}\vee U_{0}$ , with $L_{0}$ and $U_{0}$ given explicitly in Lemmas 11 and 12, respectively, and

\[ \Gamma(\alpha,q) = \min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha},\frac{q}{2}\bigg\}. \]

5.1. Regularity estimates

To prove Theorem 2, we first need to establish the space and time regularity properties of $u_{\Delta}$ , which are crucial for proving the convergence of $u_{\Delta}$ to u and determining its convergence rate. Before showing our regularity estimates of $u_{\Delta}$ , we set

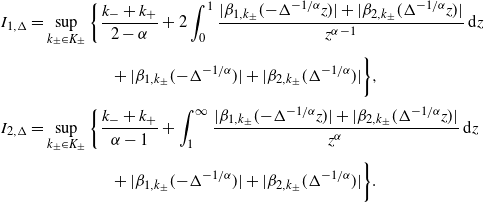\begin{align*} I_{1,\Delta} & = \sup\limits_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{2-\alpha} + 2\int_{0}^{1}\frac{|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)|+|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|} {z^{\alpha-1}}\,\textrm{d} z \\[2pt] & \qquad\qquad\quad + |\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}})| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})|\bigg\}, \\[2pt] I_{2,\Delta} & = \sup\limits_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{\alpha-1} + \int_{1}^{\infty}\frac{|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)|+|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|} {z^{\alpha}}\,\textrm{d} z \\[2pt] & \qquad\qquad\quad + |\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}})| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})|\bigg\}.\end{align*}

Theorem 3. Suppose that Assumptions 1 and 3 hold, and $\phi\in C_\textrm{b,Lip}(\mathbb{R})$ . Then:

1. (i) for any $t\in\lbrack0,T]$ and $x,y\in \mathbb{R}$ , $\vert u_{\Delta}(t,x) - u_{\Delta}(t,y)\vert \leq C_{\phi}|x-y|$ ;

2. (ii) for any $t,s\in\lbrack0,T]$ and $x\in \mathbb{R}$ , $\vert u_{\Delta}(t,x) - u_{\Delta}(s,x)\vert \leq C_{\phi}I_{\Delta}(|t-s|^{1/2}+\Delta^{1/2})$ ;

where $C_{\phi}$ is the Lipschitz constant of $\phi$ and, $I_{\Delta}=\sqrt{I_{1,\Delta}}+2I_{2,\Delta}$ with $I_{\Delta}<\infty$ .

Notice that $\tilde{\mathbb{E}}[\xi^{2}]=\infty$ , so the classical method developed in [28] fails. To prove Theorem 3, for fixed $N>0$ , we define $\xi^{N}\;:\!=\;\xi\mathbf{1}_{\{|\xi|\leq N\}}$ and introduce the truncated scheme $u_{\Delta,N}\colon[0,T]\times \mathbb{R\rightarrow R}$ recursively by

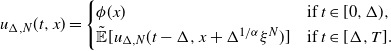(7) \begin{equation} u_{\Delta,N}(t,x) = \left\{ \begin{array}[c]{l@{\quad}l} \phi(x) & \text{if } t\in \lbrack0,\Delta), \\[2pt] \tilde{\mathbb{E}}[u_{\Delta,N}(t-\Delta,x+\Delta^{{1}/{\alpha}}\xi^{N})] & \text{if } t\in\lbrack \Delta,T]. \end{array} \right.\end{equation}

We get the following estimates.

Lemma 5. For each fixed $N>0$ , $\tilde{\mathbb{E}}[|\xi^{N}|^{2}]=N^{2-\alpha}I_{1,N}$ , where

\[ I_{1,N} \;:\!=\; \sup_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{2-\alpha} + 2\int_{0}^{1}\frac{\beta_{1,k_{\pm}}(\!-zN)+\beta_{2,k_{\pm}}(zN)}{z^{\alpha-1}}\,\textrm{d} z - \beta_{1,k_{\pm}}(\!-\!N) - \beta_{2,k_{\pm}}(N)\bigg\}. \]

Proof. Using Fubini’s theorem,

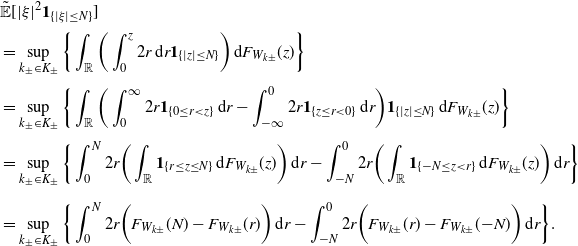\begin{align*} & \tilde{\mathbb{E}}[|\xi|^{2}\mathbf{1}_{\{|\xi|\leq N\}}] \\[2pt] & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{\mathbb{R}}\bigg(\int_{0}^{z}2r\,\textrm{d} r\mathbf{1}_{\{|z|\leq N\}}\bigg)\,\textrm{d} F_{W_{k\pm}}(z)\bigg\} \\[2pt] & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{\mathbb{R}}\bigg(\int_{0}^{\infty}2r\mathbf{1}_{\{0\leq r<z\}}\,\textrm{d} r - \int_{-\infty}^{0}2r\mathbf{1}_{\{z\leq r<0\}}\,\textrm{d} r\bigg)\mathbf{1}_{\{|z|\leq N\}}\,\textrm{d} F_{W_{k\pm}}(z)\bigg\} \\[2pt] & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{0}^{N}2r\bigg(\int_{\mathbb{R}}\mathbf{1}_{\{r\leq z\leq N\}}\,\textrm{d} F_{W_{k\pm}}(z)\bigg)\,\textrm{d} r - \int_{-N}^{0}2r\bigg(\int_{\mathbb{R}}\mathbf{1}_{\{-N\leq z<r\}}\,\textrm{d} F_{W_{k\pm}}(z)\bigg)\,\textrm{d} r\bigg\} \\[5pt] & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{0}^{N}2r\bigg(F_{W_{k\pm}}(N)-F_{W_{k\pm}}(r)\bigg)\,\textrm{d} r - \int_{-N}^{0}2r\bigg(F_{W_{k\pm}}(r)-F_{W_{k\pm}}(\!-\!N)\bigg)\,\textrm{d} r\bigg\}. \end{align*}

By changing variables, it is straightforward to check that

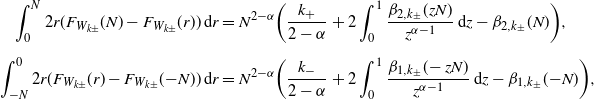\begin{align*} \int_{0}^{N}2r(F_{W_{k\pm}}(N)-F_{W_{k\pm}}(r))\,\textrm{d} r & = N^{2-\alpha}\bigg(\frac{k_{+}}{2-\alpha} + 2\int_{0}^{1}\frac{\beta_{2,k_{\pm}}(zN)}{z^{\alpha-1}}\,\textrm{d} z - \beta_{2,k_{\pm}}(N)\bigg), \\[5pt] \int_{-N}^{0}2r(F_{W_{k\pm}}(r)-F_{W_{k\pm}}(\!-\!N))\,\textrm{d} r & = N^{2-\alpha}\bigg(\frac{k_{-}}{2-\alpha} + 2\int_{0}^{1}\frac{\beta_{1,k_{\pm}}(\!-zN)}{z^{\alpha-1}}\,\textrm{d} z - \beta_{1,k_{\pm}}(\!-\!N)\bigg), \end{align*}

which immediately implies the result.

Lemma 6. For each fixed $N>0$ , $\tilde{\mathbb{E}}[|\xi-\xi^{N}|]=N^{1-\alpha}I_{2,N}$ , where

\[ I_{2,N} \;:\!=\; \sup_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{\alpha-1} + \beta_{1,k_{\pm}}(\!-\!N) + \beta_{2,k_{\pm}}(N) + \int_{1}^{+\infty}\frac{\beta_{1,k_{\pm}}(\!-zN)+\beta_{2,k_{\pm}}(zN)}{z^{\alpha}}\,\textrm{d} z\bigg\}. \]

Proof. Notice that

(8) \begin{equation} \tilde{\mathbb{E}}[|\xi-\xi^{N}|] = \tilde{\mathbb{E}}\big[|\xi|\mathbf{1}_{\{|\xi|>N\}}\big] = \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}|z|\mathbf{1}_{\{|z|>N\}}\,\textrm{d} F_{W_{k\pm}}(z)\bigg\}. \end{equation}

Observe by Fubini’s theorem that

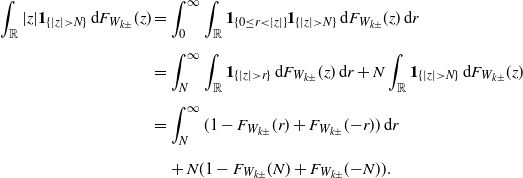(9) \begin{align} \int_{\mathbb{R}}|z|\mathbf{1}_{\{|z|>N\}}\,\textrm{d} F_{W_{k\pm}}(z) & = \int_{0}^{\infty}\int_{\mathbb{R}}\mathbf{1}_{\{0\leq r<|z|\}}\mathbf{1}_{\{|z|>N\}}\,\textrm{d} F_{W_{k\pm}}(z)\,\textrm{d} r \nonumber \\[5pt] & = \int_{N}^{\infty}\int_{\mathbb{R}}\mathbf{1}_{\{|z|>r\}}\,\textrm{d} F_{W_{k\pm}}(z)\,\textrm{d} r + N\int_{\mathbb{R}}\mathbf{1}_{\{|z|>N\}}\,\textrm{d} F_{W_{k\pm}}(z) \nonumber \\[5pt] & = \int_{N}^{\infty}(1-F_{W_{k\pm}}(r)+F_{W_{k\pm}}(\!-\!r))\,\textrm{d} r \nonumber \\[5pt] & \quad + N(1-F_{W_{k\pm}}(N)+F_{W_{k\pm}}(\!-\!N)). \end{align}

Using (8) and (9), we obtain

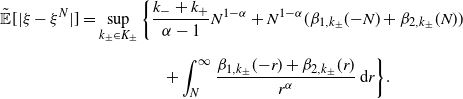\begin{align*} \tilde{\mathbb{E}}[|\xi-\xi^{N}|] & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{\alpha-1}N^{1-\alpha} + N^{1-\alpha}(\beta_{1,k_{\pm}}(\!-\!N) + \beta_{2,k_{\pm}}(N)) \\[5pt] & \qquad\qquad\quad + \int_{N}^{\infty}\frac{\beta_{1,k_{\pm}}(\!-\!r)+\beta_{2,k_{\pm}}(r)}{r^{\alpha}}\,\textrm{d} r\bigg\}. \end{align*}

By changing variables, we immediately conclude the proof.

Lemma 7. Suppose that $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ . Then:

1. (i) for any $k\in\mathbb{N}$ such that $k\Delta \leq T$ and $x,y\in \mathbb{R}$ , $\vert u_{\Delta,N}(k\Delta,x)-u_{\Delta,N}(k\Delta,y)\vert \leq C_{\phi}|x-y|$ ;

2. (ii) for any $k\in \mathbb{N}$ such that $k\Delta \leq T$ and $x\in \mathbb{R}$ ,

   \begin{align*} \vert u_{\Delta,N}(k\Delta,x)-u_{\Delta,N}(0,x)\vert & \leq C_{\phi}\big((I_{1,N})^{{1}/{2}}N^{({2-\alpha})/{2}}\Delta^{({2-\alpha})/{2\alpha}} \\[5pt] & \qquad\quad + I_{2,N}N^{1-\alpha}\Delta^{({1-\alpha})/{\alpha}}\big)(k\Delta)^{{1}/{2}}; \end{align*}

where $C_{\phi}$ is the Lipschitz constant of $\phi$ , and $I_{1,N}$ , $I_{2,N}$ are given in Lemmas 5 and 6, respectively.

Proof. Assertion (i) is proved by induction using (7). Clearly, the estimate holds for $k=0$ . In general, we assume the assertion holds for some $k\in\mathbb{N}$ with $k\Delta\leq T$ . Then, using Proposition 1, we have

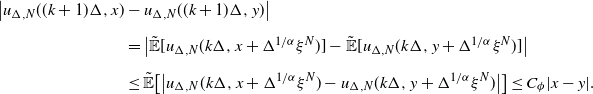\begin{align*} \big\vert u_{\Delta,N}((k+1)\Delta,x) & - u_{\Delta,N}((k+1)\Delta,y)\big\vert \\[5pt] & = \big\vert\tilde{\mathbb{E}}[u_{\Delta,N}(k\Delta,x+\Delta^{{1}/{\alpha}}\xi^{N})] - \tilde{\mathbb{E}}[u_{\Delta,N}(k\Delta,y+\Delta^{{1}/{\alpha}}\xi^{N})]\big\vert \\[5pt] & \leq \tilde{\mathbb{E}}\big[\big\vert u_{\Delta,N}(k\Delta,x+\Delta^{{1}/{\alpha}}\xi^{N}) - u_{\Delta,N}(k\Delta,y+\Delta^{{1}/{\alpha}}\xi^{N})\big\vert\big] \leq C_{\phi}|x-y|. \end{align*}

By the principle of induction the assertion is true for all $k\in \mathbb{N}$ with $k\Delta \leq T$ .

Now we establish the time regularity for $u_{\Delta,N}$ in (ii). Note that Young’s inequality implies that, for any $x,y>0$ , $xy\leq \frac{1}{2}(x^{2}+y^{2})$ . For any $\varepsilon>0$ , let $x=|x-y|$ and $y={1}/{\varepsilon}$ ; then it follows from (i) that

\[ u_{\Delta,N}(k\Delta,x)\leq u_{\Delta,N}(k\Delta,y)+A|x-y|^{2}+B, \]

where $A=({\varepsilon}/{2})C_{\phi}$ and $B=({1}/{2\varepsilon})C_{\phi}$ .

We claim that, for any $k\in \mathbb{N}$ such that $k\Delta \leq T$ and $x,y\in \mathbb{R}$ ,

(10) \begin{equation} u_{\Delta,N}(k\Delta,x) \leq u_{\Delta,N}(0,y)+A|x-y|^{2}+AM_{N}^{2}k\Delta^{{2}/{\alpha}} + C_{\phi}D_{N}k\Delta^{{1}/{\alpha}} + B, \end{equation}

where $M_{N}^{2}=\tilde{\mathbb{E}}[|\xi^{N}|^{2}]$ and $D_{N}=\tilde{\mathbb{E}}[|\xi-\xi^{N}|]$ . Indeed, (10) obviously holds for $k=0$ . Assume that for some $k\in \mathbb{N}$ the assertion (10) holds. Notice that

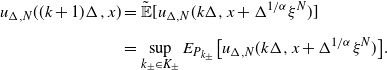(11) \begin{align} u_{\Delta,N}((k+1)\Delta,x) & = \tilde{\mathbb{E}}[u_{\Delta,N}(k\Delta,x+\Delta^{{1}/{\alpha}}\xi^{N})] \nonumber \\[5pt] & = \sup_{k_{\pm}\in K_{\pm}}E_{P_{k_{\pm}}}\big[u_{\Delta,N}(k\Delta,x+\Delta^{{1}/{\alpha}}\xi^{N})\big]. \end{align}

Then, for any $k_{\pm}\in K_{\pm}$ ,

(12) \begin{align} E_{P_{k_{\pm}}}[u_{\Delta,N}(k\Delta,x+\Delta^{{1}/{\alpha}}\xi^{N})] & \leq u_{\Delta,N}(0,y+\Delta^{{1}/{\alpha}}E_{P_{k_{\pm}}}[\xi^{N}]) + AM_{N}^{2}k\Delta^{{2}/{\alpha}} + C_{\phi}D_{N}k\Delta^{{1}/{\alpha}} \nonumber \\[5pt] & \quad + B + AE_{P_{k_{\pm}}}\big[\big|x-y+\Delta^{{1}/{\alpha}}(\xi^{N}-E_{P_{k_{\pm}}}[\xi^{N}])\big|^{2}\big]. \end{align}

Seeing that $E_{P_{k_{\pm}}}\big[\xi^{N}-E_{P_{k_{\pm}}}[\xi^{N}]\big]=0$ and

\[ E_{P_{k_{\pm}}}\big[\big(\xi^{N}-E_{P_{k_{\pm}}}[\xi^{N}]\big)^{2}\big] = E_{P_{k_{\pm}}}\big[(\xi^{N})^{2}\big]-\big(E_{P_{k_{\pm}}}[\xi^{N}]\big)^{2} \leq \tilde{\mathbb{E}}\big[|\xi^{N}|^{2}\big], \]

we can deduce that

(13) \begin{equation} E_{P_{k_{\pm}}}\big[\big|x-y+\Delta^{{1}/{\alpha}}\big(\xi^{N}-E_{P_{k_{\pm}}}[\xi^{N}]\big)\big|^{2}\big] \leq |x-y|^{2} + M_{N}^{2}\Delta^{{2}/{\alpha}}. \end{equation}

Also, since $E_{P_{k_{\pm}}}[\xi]=0$ , it follows from (i) that

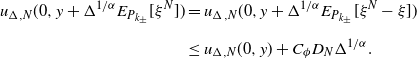(14) \begin{align} u_{\Delta,N}(0,y+\Delta^{{1}/{\alpha}}E_{P_{k_{\pm}}}[\xi^{N}]) & = u_{\Delta,N}(0,y+\Delta^{{1}/{\alpha}}E_{P_{k_{\pm}}}[\xi^{N}-\xi]) \nonumber \\[5pt] & \leq u_{\Delta,N}(0,y) + C_{\phi}D_{N}\Delta^{{1}/{\alpha}}. \end{align}

Combining (11)–(14), we obtain

\[ u_{\Delta,N}((k+1)\Delta,x) \leq u_{\Delta,N}(0,y) + A|x-y|^{2}+AM_{N}^{2}(k+1)\Delta^{{2}/{\alpha}} + C_{\phi}D_{N}(k+1)\Delta^{{1}/{\alpha}} + B, \]

which shows that (10) also holds for $k+1$ . By the principle of induction our claim is true for all $k\in \mathbb{N}$ such that $k\Delta \leq T$ and $x,y\in \mathbb{R}$ . By taking $y=x$ in (10) we have, for any $\varepsilon>0$ ,

\[ u_{\Delta,N}(k\Delta,x) \leq u_{\Delta,N}(0,x) + \frac{\varepsilon}{2}C_{\phi}M_{N}^{2}k\Delta^{{2}/{\alpha}} + C_{\phi}D_{N}k\Delta^{{1}/{\alpha}} + \frac{1}{2\varepsilon}C_{\phi}. \]

By minimizing of the right-hand side with respect to $\varepsilon$ , we obtain

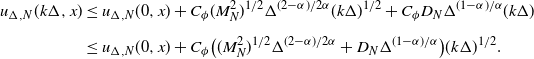\begin{align*} u_{\Delta,N}(k\Delta,x) & \leq u_{\Delta,N}(0,x) + C_{\phi}(M_{N}^{2})^{{1}/{2}}\Delta^{({2-\alpha})/{2\alpha}}(k\Delta)^{{1}/{2}} + C_{\phi}D_{N}\Delta^{({1-\alpha})/{\alpha}}(k\Delta) \\[5pt] & \leq u_{\Delta,N}(0,x) + C_{\phi}\big((M_{N}^{2})^{{1}/{2}}\Delta^{({2-\alpha})/{2\alpha}} + D_{N}\Delta^{({1-\alpha})/{\alpha}}\big)(k\Delta)^{{1}/{2}}. \end{align*}

Similarly, we also have

\[ u_{\Delta,N}(0,x) \leq u_{\Delta,N}(k\Delta,x) + C_{\phi}\big((M_{N}^{2})^{{1}/{2}}\Delta^{({2-\alpha})/{2\alpha}} + D_{N}\Delta^{({1-\alpha})/{\alpha}}\big)(k\Delta)^{{1}/{2}}. \]

Combining with Lemmas 5 and 6, we obtain our desired result (ii).

Lemma 8. Suppose that $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ and $N>0$ is fixed. Then, for any $k\in \mathbb{N}$ such that $k\Delta \leq T$ and $x\in \mathbb{R}$ ,

\[ vert u_{\Delta}(k\Delta,x) - u_{\Delta,N}(k\Delta,x)\vert \leq C_{\phi}I_{2,N}N^{1-\alpha}\Delta^{({1-\alpha})/{\alpha}}k\Delta, \]

where $C_{\phi}$ is the Lipschitz constant of $\phi$ and $I_{2,N}$ is given in Lemma 6.

Proof. Let $(\xi_{i})_{i\geq1}$ be a sequence of random variables on $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ such that $\xi_{1}=\xi$ , $\xi_{i+1}\overset{\textrm{d}}{=}\xi_{i}$ , and $\xi_{i+1}\perp(\xi_{1},\xi_{2},\ldots,\xi_{i})$ for each $i\in \mathbb{N}$ , and let $\xi_{i}^{N}=\xi_{i}\wedge N\vee(\!-\!N)$ for each $i\in \mathbb{N}$ . In view of (6) and (7), by using the induction method of [20, Theorem 2.1] we have, for any $k\in \mathbb{N}$ such that $k\Delta \leq T$ and $x\in \mathbb{R}$ ,

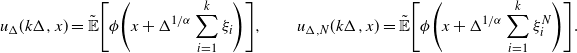\begin{equation*} u_{\Delta}(k\Delta,x) = \tilde{\mathbb{E}}\Bigg[\phi\Bigg(x + \Delta^{{1}/{\alpha}}\sum\limits_{i=1}^{k}\xi_{i}\Bigg)\Bigg], \qquad u_{\Delta,N}(k\Delta,x) = \tilde{\mathbb{E}}\Bigg[\phi\Bigg(x + \Delta^{{1}/{\alpha}}\sum\limits_{i=1}^{k}\xi_{i}^{N}\Bigg)\Bigg]. \end{equation*}

Then, it follows from the Lipschitz condition of $\phi$ and Lemma 6 that

\begin{equation*} \!\qquad\quad \vert u_{\Delta}(k\Delta,x)-u_{\Delta,N}(k\Delta,x)\vert \leq C_{\phi}\Delta^{{1}/{\alpha}}k\tilde{\mathbb{E}}[|\xi_{1}-\xi_{1}^{N}|] \leq C_{\phi}I_{2,N}N^{1-\alpha}\Delta^{({1-\alpha})/{\alpha}}k\Delta.\qquad \square \end{equation*}

Now we start to prove the regularity results of $u_{\Delta}$ .

Proof of Theorem 3. The space regularity of $u_{\Delta}$ can be proved by induction using (6). We only focus on the time regularity of $u_{\Delta}$ and divide its proof into three steps.

Step 1. Consider the special case $\vert u_{\Delta}(k\Delta,\cdot)-u_{\Delta}(0,\cdot)\vert $ for any $k\in \mathbb{N}$ such that $k\Delta \leq T$ . Noting that $u_{\Delta,N}(0,x)=u_{\Delta}(0,x)=\phi(x)$ , we have

\[ \vert u_{\Delta}(k\Delta,x)-u_{\Delta}(0,x)\vert \leq \vert u_{\Delta}(k\Delta,x)-u_{\Delta,N}(k\Delta,x)\vert + \vert u_{\Delta,N}(k\Delta,x)-u_{\Delta,N}(0,x)\vert . \]

In view of Lemmas 7 and 8, by choosing $N=\Delta^{-{1}/{\alpha}}$ we obtain

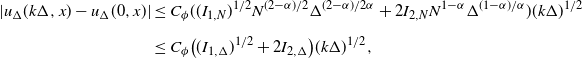(15) \begin{align} \vert u_{\Delta}(k\Delta,x)-u_{\Delta}(0,x)\vert & \leq C_{\phi}((I_{1,N})^{{1}/{2}}N^{({2-\alpha})/{2}}\Delta^{({2-\alpha})/{2\alpha}} + 2I_{2,N}N^{1-\alpha}\Delta^{({1-\alpha})/{\alpha}})(k\Delta)^{{1}/{2}} \nonumber \\[5pt] & \leq C_{\phi}\big((I_{1,\Delta})^{{1}/{2}} + 2I_{2,\Delta}\big)(k\Delta)^{{1}/{2}}, \end{align}

where

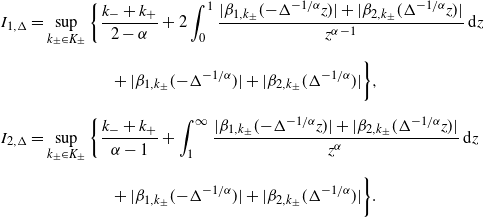\begin{align*} I_{1,\Delta} & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{2-\alpha} + 2\int_{0}^{1}\frac{|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)|+|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|} {z^{\alpha-1}}\,\textrm{d} z \\[5pt] & \qquad\qquad\quad + |\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}})| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})|\bigg\}, \\[5pt] I_{2,\Delta} & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{\frac{k_{-}+k_{+}}{\alpha-1} + \int_{1}^{\infty}\frac{|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)|+|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|} {z^{\alpha}}\,\textrm{d} z \\[5pt] & \qquad\qquad\quad + |\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}})| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})|\bigg\}. \end{align*}

In addition, by Assumption 1, it is easy to obtain that $I_{1,\Delta}$ and $I_{2,\Delta}$ are finite as $\Delta \rightarrow0$ .

Step 2. Let us turn to the case $\vert u_{\Delta}(k\Delta,\cdot)-u_{\Delta}(l\Delta,\cdot)\vert$ for any $k,l\in \mathbb{N}$ such that $(k\vee l)\Delta \leq T$ . Without loss of generality, we assume that $k\geq l$ . Let $(\xi_{i})_{i=1}^{\infty}$ be a sequence of random variables on $(\mathbb{R},C_\textrm{Lip}(\mathbb{R}),\tilde{\mathbb{E}})$ such that $\xi_{1}=\xi$ , $\xi_{i+1}\overset{\textrm{d}}{=}\xi_{i}$ , and $\xi_{i+1}\perp(\xi_{1},\xi_{2},\ldots,\xi_{i})$ for each $i\in\mathbb{N}$ . By using induction (6) and the estimate (15), it is easy to obtain that, for any $k\geq l$ and $x\in \mathbb{R}$ ,

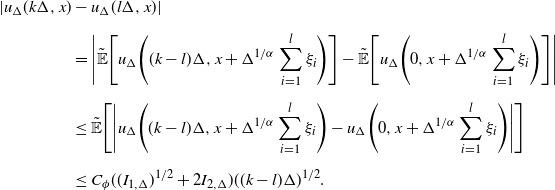(16) \begin{align} \vert u_{\Delta}(k\Delta,x) & - u_{\Delta}(l\Delta,x)\vert \nonumber \\[5pt] & = \Bigg\vert\tilde{\mathbb{E}}\Bigg[u_{\Delta}\Bigg((k-l)\Delta, x+\Delta^{{1}/{\alpha}}\sum_{i=1}^{l}\xi_{i}\Bigg)\Bigg] - \tilde{\mathbb{E}}\Bigg[u_{\Delta}\Bigg(0,x+\Delta^{{1}/{\alpha}}\sum_{i=1}^{l}\xi_{i}\Bigg)\Bigg]\Bigg\vert \nonumber \\[5pt] & \leq \tilde{\mathbb{E}}\Bigg[\Bigg\vert u_{\Delta}\Bigg((k-l)\Delta,x+\Delta^{{1}/{\alpha}}\sum_{i=1}^{l}\xi_{i}\Bigg) - u_{\Delta}\Bigg(0,x+\Delta^{{1}/{\alpha}}\sum_{i=1}^{l}\xi_{i}\Bigg)\Bigg\vert\Bigg] \nonumber \\[5pt] & \leq C_{\phi}((I_{1,\Delta})^{{1}/{2}}+2I_{2,\Delta})((k-l)\Delta)^{{1}/{2}}. \end{align}

Step 3. In general, for $s,t\in \lbrack0,T]$ , let $\delta_{s},\delta_{t}\in \lbrack0,\Delta)$ such that $s-\delta_{s}$ and $t-\delta_{t}$ are in the grid points $\{k\Delta\colon k\in \mathbb{N}\}$ . Then, from (16),

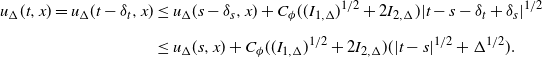\begin{align*} u_{\Delta}(t,x) = u_{\Delta}(t-\delta_{t},x) & \leq u_{\Delta}(s-\delta_{s},x) + C_{\phi}((I_{1,\Delta})^{{1}/{2}} + 2I_{2,\Delta})|t-s-\delta_{t}+\delta_{s}|^{{1}/{2}} \\[5pt] & \leq u_{\Delta}(s,x) + C_{\phi}((I_{1,\Delta})^{{1}/{2}} + 2I_{2,\Delta})(|t-s|^{{1}/{2}}+\Delta^{{1}/{2}}). \end{align*}

We can similarly prove that

\[ u_{\Delta}(s,x) \leq u_{\Delta}(t,x) + C_{\phi}((I_{1,\Delta})^{{1}/{2}} + 2I_{2,\Delta})(|t-s|^{{1}/{2}} + \Delta^{{1}/{2}}), \]

and this yields (ii).

5.2. The monotone approximation scheme

In this section we first rewrite the recursive approximation (6) as a monotone scheme, and then derive its consistency error estimates and comparison result.

For $\Delta \in(0,1)$ , based on (6), we introduce the monotone approximation scheme as

(17) \begin{equation} \left \{ \begin{array}[c]{l@{\quad}l} S(\Delta,x,u_{\Delta}(t,x),u_{\Delta}(t-\Delta,\cdot))=0, & (t,x)\in\lbrack\Delta,T]\times\mathbb{R}, \\[5pt] u_{\Delta}(t,x)=\phi(x), & (t,x)\in \lbrack0,\Delta)\times\mathbb{R}, \end{array} \right. \end{equation}

where $S\colon(0,1)\times\mathbb{R}\times\mathbb{R}\times C_\textrm{b}(\mathbb{R}){\rightarrow R}$ is defined by

(18) \begin{equation} S(\Delta,x,p,v) = \frac{p-\tilde{\mathbb{E}}[v(x+\Delta^{{1}/{\alpha}}\xi)]}{\Delta}. \end{equation}

For a function f defined on $[0,T]\times \mathbb{R}$ , introduce its norm $|f|_{0}\;:\!=\;\sup_{[0,T]\times \mathbb{R}}|f(t,x)|$ . We now give some key properties of the approximation scheme (17).

Proposition 2. Suppose that $S(\Delta,x,p,v)$ is as given in (18). Then the following properties hold:

1. (i) Monotonicity. For any $c_{1},c_{2}\in \mathbb{R}$ and any function $u\in C_{b}(\mathbb{R})$ with $u\leq v$ ,

   \[ S(\Delta,x,p+c_{1},u+c_{2})\geq S(\Delta,x,p,v)+\frac{c_{1}-c_{2}}{\Delta}. \]

2. (ii) Concavity. For any $\lambda \in[0,1]$ , $p_{1},p_{2}\in \mathbb{R}$ , and $v_{1},v_{2}\in C_\textrm{b}(\mathbb{R})$ , $S(\Delta,x,p,v)$ is concave in (p,v), i.e.

   \begin{align*} S(\Delta,x,\lambda p_{1}&+(1-\lambda)p_{2},\lambda v_{1}(\cdot)+(1-\lambda)v_{2}(\cdot)) \geq \lambda S(\Delta,x,p_{1},v_{1}(\cdot))\\[5pt] &+(1-\lambda)S(\Delta,x,p_{2},v_{2}(\cdot)). \end{align*}

3. (iii) Consistency. For any $\omega \in C_\textrm{b}^{\infty}([\Delta,T]\times \mathbb{R})$ ,

   \begin{align*} & \bigg\vert\partial_{t}\omega(t,x) - \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}\delta_{z}\omega(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} - S(\Delta,x,\omega(t,x),\omega(t-\Delta,\cdot))\bigg\vert \\[5pt] &\leq \big(1+\tilde{\mathbb{E}}[|\xi|]\big) \big(|\partial_{t}^{2}\omega|_{0}\Delta + |\partial_{t}D_{x}\omega|_{0}\Delta^{{1}/{\alpha}}\big) + R^{0}|D_{x}^{2}\omega|_{0}\Delta^{({2-\alpha})/{\alpha}}\\[5pt] &\quad + |D_{x}^{2}\omega|_{0}R_{\Delta}^{1} + \vert D_{x}\omega\vert_{0}R_{\Delta}^{2}, \end{align*}
   where
   \begin{align*} R^{0} & = \sup_{k_{\pm}\in K_{\pm}}\bigg\{|\beta_{1,k_{\pm}}(\!-\!1)| + |\beta_{2,k_{\pm}}(1)| \\[5pt] & \qquad\qquad\quad + \int_{0}^{1}\big[|\alpha\beta_{1,k_{\pm}}(\!-z)+\beta_{1,k_{\pm}}^{\prime}(\!-z)z| + |\alpha\beta_{2,k_{\pm}}(z) - \beta_{2,k_{\pm}}^{\prime}(z)z|\big]z^{1-\alpha}\,\textrm{d} z\bigg\}, \\[5pt] R_{\Delta}^{1} & = 5\sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{0}^{1}\big[|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|\big]z^{1-\alpha}\,\textrm{d} z\bigg\}, \\[5pt] R_{\Delta}^{2} & = 4\sup_{k_{\pm}\in K_{\pm}}\bigg\{|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}})| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})| \\[5pt] & \qquad\qquad\quad + \int_{1}^{\infty}\big[|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|\big]z^{-\alpha}\,\textrm{d} z\bigg\}. \end{align*}

Proof. Parts (i) and (ii) are immediate, so we only prove (iii). To this end, we split the consistency error into two parts. Specifically, for $(t,x)\in[\Delta,T]\times \mathbb{R}$ ,

(19) \begin{align} & \bigg\vert\partial_{t}\omega(t,x) - \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}\delta_{z}\omega(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} - S(\Delta,x,\omega(t,x),\omega(t-\Delta,\cdot))\bigg\vert \nonumber \\[5pt] & \leq \Delta^{-1}\big\vert\tilde{\mathbb{E}}[\omega(t-\Delta,x+\Delta^{{1}/{\alpha}}\xi)] - \tilde{\mathbb{E}}[\omega(t,x+\Delta^{{1}/{\alpha}}\xi)-D_{x}\omega(t,x)\Delta^{{1}/{\alpha}}\xi] + \partial_{t}\omega(t,x)\Delta\big\vert \nonumber \\[5pt] & \quad + \Delta^{-1}\bigg\vert\tilde{\mathbb{E}}[\delta_{\Delta^{1/\alpha}\xi}\omega(t,x)] - \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}\delta_{z}\omega(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\}\Delta\bigg\vert \;:\!=\; I + II. \end{align}

Applying Taylor’s expansion (twice) yields

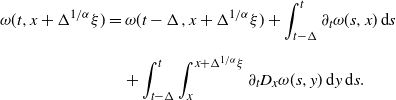(20) \begin{align} \omega(t,x+\Delta^{{1}/{\alpha}}\xi) & = \omega(t-\Delta,x+\Delta^{{1}/{\alpha}}\xi) + \int_{t-\Delta}^{t}\partial_{t}\omega(s,x)\,\textrm{d} s \nonumber \\[5pt] & \quad + \int_{t-\Delta}^{t}\int_{x}^{x+\Delta^{1/\alpha}\xi}\partial_{t}D_{x}\omega(s,y)\,\textrm{d} y\,\textrm{d} s. \end{align}

Since $\tilde{\mathbb{E}}[\xi]=\tilde{\mathbb{E}}[-\xi]=0$ , (20) and the mean value theorem give

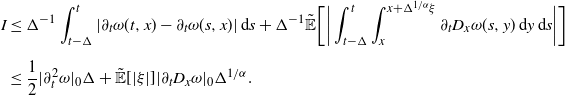(21) \begin{align} I & \leq \Delta^{-1}\int_{t-\Delta}^{t}\vert\partial_{t}\omega(t,x)-\partial_{t}\omega(s,x)\vert\,\textrm{d} s + \Delta^{-1}\tilde{\mathbb{E}}\bigg[\bigg\vert \int_{t-\Delta}^{t}\int_{x}^{x+\Delta^{1/\alpha}\xi}\partial_{t}D_{x}\omega(s,y)\,\textrm{d} y\,\textrm{d} s\bigg\vert\bigg] \nonumber \\[5pt] & \leq \frac{1}{2}|\partial_{t}^{2}\omega|_{0}\Delta + \tilde{\mathbb{E}}[|\xi|]|\partial_{t}D_{x}\omega|_{0}\Delta^{{1}/{\alpha}}. \end{align}

For II, by changing variables we get

\begin{align*} II & \leq \sup_{k_{\pm}\in K_{\pm}}\bigg\{\bigg\vert\int_{\mathbb{-\infty}}^{0} \delta_{z}\omega(t,x)[\!-\!\beta_{1,k_{\pm}}^{\prime}(\Delta^{-{1}/{\alpha}}z)\Delta^{-{1}/{\alpha}}z + \alpha\beta_{1,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)]|z|^{-\alpha-1}\,\textrm{d} z \\[5pt] & \qquad\qquad\quad + \int_{0}^{\infty}\delta_{z}\omega(t,x) \big[{-}\beta_{2,k_{\pm}}^{\prime}(\Delta^{-{1}/{\alpha}}z)\Delta^{-{1}/{\alpha}}z + \alpha\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)\big]z^{-\alpha-1}\,\textrm{d} z\bigg\vert\bigg\}. \end{align*}

We only consider the integral above along the positive half-line; the integral along the negative half-line is similar. For simplicity, we set

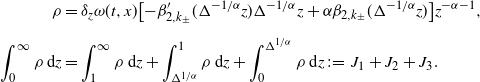\begin{align*} \rho & = \delta_{z}\omega(t,x)\big[{-}\beta_{2,k_{\pm}}^{\prime}(\Delta^{-{1}/{\alpha}}z)\Delta^{-{1}/{\alpha}}z + \alpha\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)\big]z^{-\alpha-1}, \\[5pt] \int_{0}^{\infty}\rho\,\textrm{d} z & = \int_{1}^{\infty}\rho\,\textrm{d} z + \int_{\Delta^{1/\alpha}}^{1}\rho\,\textrm{d} z + \int_{0}^{\Delta^{1/\alpha}}\rho\,\textrm{d} z \;:\!=\; J_{1} + J_{2} + J_{3}. \end{align*}

Using integration by parts, for any $k_{\pm}\in K_{\pm}$ ,

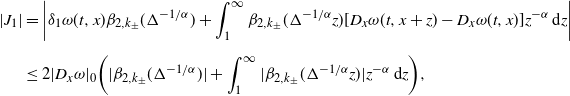\begin{align*} |J_{1}| & = \bigg\vert\delta_{1}\omega(t,x)\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}) + \int_{1}^{\infty}\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z) [D_{x}\omega(t,x+z)-D_{x}\omega(t,x)]z^{-\alpha}\,\textrm{d} z\bigg\vert \\[5pt] & \leq 2\vert D_{x}\omega\vert_{0}\bigg (|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})| + \int_{1}^{\infty}|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|z^{-\alpha}\,\textrm{d} z\bigg), \end{align*}

where we have used the fact that, for $\theta \in(0,1)$ ,

\[ |\delta_{1}\omega(t,x)|=|D_{x}\omega(t,x+\theta)-D_{x}\omega(t,x)|\leq2|D_{x}\omega|_{0}. \]

Notice that, for any $k_{\pm}\in K_{\pm}$ ,

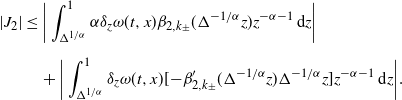\begin{align*} |J_{2}| & \leq \bigg\vert\int_{\Delta^{1/\alpha}}^{1}\alpha\delta_{z}\omega(t,x)\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z) z^{-\alpha-1}\,\textrm{d} z\bigg\vert \\[5pt] & \quad + \bigg\vert\int_{\Delta^{1/\alpha}}^{1}\delta_{z}\omega(t,x) [\!-\!\beta_{2,k_{\pm}}^{\prime}(\Delta^{-{1}/{\alpha}}z)\Delta^{-{1}/{\alpha}}z]z^{-\alpha-1}\,\textrm{d} z\bigg\vert. \end{align*}

By means of integration by parts and the mean value theorem, we obtain

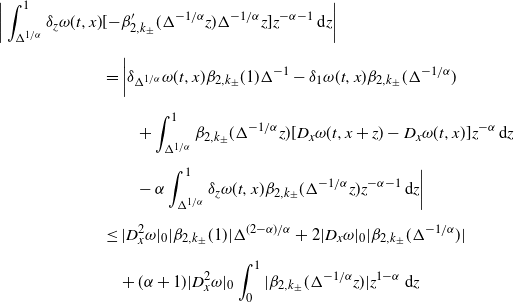\begin{align*} \bigg\vert\int_{\Delta^{1/\alpha}}^{1}\delta_{z}\omega(t,x) & [\!-\!\beta_{2,k_{\pm}}^{\prime}(\Delta^{-{1}/{\alpha}}z)\Delta^{-{1}/{\alpha}}z]z^{-\alpha-1}\,\textrm{d} z\bigg\vert \\[5pt] & = \bigg\vert\delta_{\Delta^{1/\alpha}}\omega(t,x)\beta_{2,k_{\pm}}(1)\Delta^{-1} - \delta_{1}\omega(t,x)\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}) \\[5pt] & \qquad + \int_{\Delta^{1/\alpha}}^{1}\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z) [D_{x}\omega(t,x+z)-D_{x}\omega(t,x)]z^{-\alpha}\,\textrm{d} z \\[5pt] & \qquad - \alpha\int_{\Delta^{1/\alpha}}^{1}\delta_{z}\omega(t,x)\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z) z^{-\alpha-1}\,\textrm{d} z\bigg\vert \\[5pt] & \leq |D_{x}^{2}\omega|_{0}|\beta_{2,k_{\pm}}(1)|\Delta^{({2-\alpha})/{\alpha}} + 2|D_{x}\omega|_{0}|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})| \\[5pt] & \quad + (\alpha+1)|D_{x}^{2}\omega|_{0}\int_{0}^{1}|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|z^{1-\alpha}\,\textrm{d} z \end{align*}

by using the fact that, for $\theta \in(0,1)$ , $|\delta_{z}\omega(t,x)|=\frac{1}{2}|D_{x}^{2}\omega(t,x+\theta z)z^{2}|\leq|D_{x}^{2}\omega|_{0}z^{2}$ ; similarly,

\[ \bigg\vert\int_{\Delta^{1/\alpha}}^{1}\alpha\delta_{z}\omega(t,x)\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z) z^{-\alpha-1}\,\textrm{d} z\bigg\vert \leq \alpha|D_{x}^{2}\omega|_{0}\int_{0}^{1}|\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|z^{1-\alpha}\,\textrm{d} z. \]

In the same way, we can also obtain

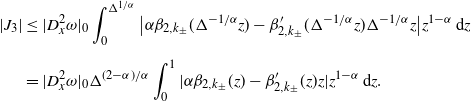\begin{align*} |J_{3}| & \leq |D_{x}^{2}\omega|_{0}\int_{0}^{\Delta^{1/\alpha}}\big\vert\alpha\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z) - \beta_{2,k_{\pm}}^{\prime}(\Delta^{-{1}/{\alpha}}z)\Delta^{-{1}/{\alpha}}z\big\vert z^{1-\alpha}\,\textrm{d} z \\[5pt] & = |D_{x}^{2}\omega|_{0}\Delta^{({2-\alpha})/{\alpha}}\int_{0}^{1}\vert\alpha\beta_{2,k_{\pm}}(z) - \beta_{2,k_{\pm}}^{\prime}(z)z\vert z^{1-\alpha}\,\textrm{d} z. \end{align*}

Together with $J_{1}$ , $J_{2}$ , and $J_{3}$ , we conclude that

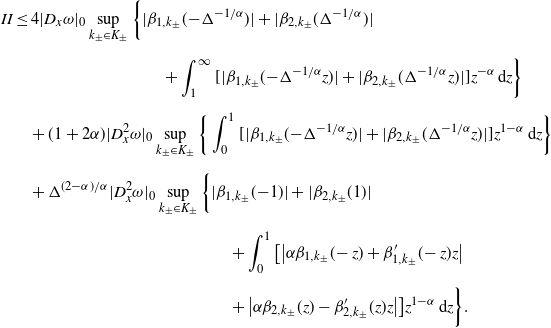\begin{align*} II & \leq 4\vert D_{x}\omega\vert_{0}\sup_{k_{\pm}\in K_{\pm}}\bigg\{|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}})| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}})| \\[5pt] & \qquad\qquad\qquad\qquad\quad + \int_{1}^{\infty}[|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|]z^{-\alpha}\,\textrm{d} z\bigg\} \\[5pt] & \quad + (1+2\alpha)|D_{x}^{2}\omega|_{0}\sup_{k_{\pm}\in K_{\pm}}\bigg\{ \int_{0}^{1}[|\beta_{1,k_{\pm}}(\!-\!\Delta^{-{1}/{\alpha}}z)| + |\beta_{2,k_{\pm}}(\Delta^{-{1}/{\alpha}}z)|]z^{1-\alpha}\,\textrm{d} z\bigg\} \\[5pt] & \quad + \Delta^{({2-\alpha})/{\alpha}}|D_{x}^{2}\omega|_{0}\sup_{k_{\pm}\in K_{\pm}} \bigg\{|\beta_{1,k_{\pm}}(\!-\!1)| + |\beta_{2,k_{\pm}}(1)| \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad\quad + \int_{0}^{1}\big[ \big|\alpha\beta_{1,k_{\pm}}(\!-z)+\beta_{1,k_{\pm}}^{\prime}(\!-z)z\big| \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad\quad + \big|\alpha\beta_{2,k_{\pm}}(z) - \beta_{2,k_{\pm}}^{\prime}(z)z\big|\big]z^{1-\alpha}\,\textrm{d} z\bigg\}. \end{align*}

The desired conclusion follows from this and (21).

From Proposition 2(i) we can derive the following comparison result for the scheme (17), which is used throughout this paper.

Lemma 9. Suppose that $\underline{v},\bar{v}\in C_\textrm{b}([0,T]\times \mathbb{R})$ satisfy

\begin{align*} S(\Delta,x,\underline{v}(t,x),\underline{v}(t-\Delta,\cdot)) & \leq h_{1} \quad \text{in } (\Delta,T]\times\mathbb{R}, \\[5pt] S(\Delta,x,\bar{v}(t,x),\bar{v}(t-\Delta,\cdot)) & \geq h_{2} \quad \text{in } (\Delta,T]\times\mathbb{R}, \end{align*}

where $h_{1},h_{2}\in C_\textrm{b}((\Delta,T]\times \mathbb{R})$ . Then

\[ \underline{v}-\bar{v}\leq \sup_{(t,x)\in \lbrack0,\Delta]\times \mathbb{R} }(\underline{v}-\bar{v})^{+}+t\sup_{(t,x)\in(\Delta,T]\times \mathbb{R}} (h_{1}-h_{2})^{+}\text{.} \]

Proof. The basic idea of the proof comes from [4, Lemma 3.2]; for the reader’s convenience, we give a sketch of the proof.

We first note that it suffices to prove the lemma in the case $\underline{v} \leq \bar{v}$ in $[0,\Delta]\times \mathbb{R}$ , $h_{1}\leq h_{2}$ in $(\Delta,T]\times \mathbb{R}$ . The general case follows from this after seeing that, from the monotonicity property in Proposition 2(i),

\[ \omega\;:\!=\;\bar{v}+\sup_{(t,x)\in \lbrack0,\Delta]\times \mathbb{R}}(\underline {v}-\bar{v})^{+}+t\sup_{(t,x)\in(\Delta,T]\times \mathbb{R}}(h_{1}-h_{2})^{+} \]

satisfies

\[ S(\Delta,x,\omega(t,x),\omega(t-\Delta,\cdot))\geq S(\Delta,x,\bar {v}(t,x),\bar{v}(t-\Delta,\cdot))+\sup_{(t,x)\in(\Delta,T]\times \mathbb{R} }(h_{1}-h_{2})^{+}\geq h_{1} \]

for $(t,x)\in(\Delta,T]\times \mathbb{R}$ , and $\underline{v}\leq \omega$ in $[0,\Delta]\times \mathbb{R}$ .

For $c\geq0$ , let $\psi_{c}(t)\;:\!=\;ct$ and $g(c)\;:\!=\;\sup_{(t,x)\in \lbrack0,T]\times \mathbb{R}}\{\underline{v}-\bar{v}-\psi_{c}\}$ . Next, we have to prove that $g(0)\leq0$ and we argue by contradiction assuming $g(0)>0$ . From the continuity of g, we can find some $c>0$ such that $g(c)>0$ . For such c, take a sequence $\{(t_{n},x_{n})\}_{n\geq1}\subset [0,T]\times\mathbb{R}$ such that, as $n\rightarrow \infty$ ,

\[ \delta_{n}\;:\!=\;g(c)-(\underline{v}-\bar{v}-\psi_{c})(t_{n},x_{n})\rightarrow0. \]

Since $\underline{v}-\bar{v}-\psi_{c}\leq0$ in $[0,\Delta]\times \mathbb{R}$ and $g(c)>0$ , we assert that $t_{n}>\Delta$ for sufficiently large n. For such n, by applying Proposition 2(i) (twice) we can deduce that

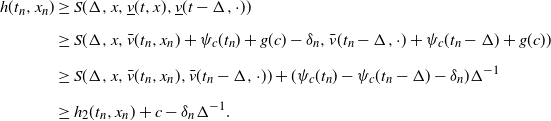\begin{align*} h(t_{n},x_{n}) & \geq S(\Delta,x,\underline{v}(t,x),\underline{v}(t-\Delta,\cdot)) \\[5pt] & \geq S(\Delta,x,\bar{v}(t_{n},x_{n})+\psi_{c}(t_{n})+g(c)-\delta_{n},\bar{v}(t_{n}-\Delta,\cdot) + \psi_{c}(t_{n}-\Delta)+g(c)) \\[5pt] & \geq S(\Delta,x,\bar{v}(t_{n},x_{n}),\bar{v}(t_{n}-\Delta,\cdot))+(\psi_{c}(t_{n}) - \psi_{c}(t_{n}-\Delta)-\delta_{n})\Delta^{-1} \\[5pt] & \geq h_{2}(t_{n},x_{n})+c-\delta_{n}\Delta^{-1}. \end{align*}

Since $h_{1}\leq h_{2}$ in $(\Delta,T]\times \mathbb{R}$ , this yields that $c-\delta_{n}\Delta^{-1}\leq0$ . By letting $n\rightarrow \infty$ , we obtain $c\leq0$ , which is a contradiction.

5.3. Convergence rate of the monotone approximation scheme

In this subsection we prove the convergence rate of the monotone approximation scheme $u_{\Delta}$ in Theorem 2. The convergence of the approximate solution $u_{\Delta}$ to the viscosity solution u follows from a nonlocal extension of the Barles–Souganidis half-relaxed limits method [5].

We start from the first time interval $[0,\Delta]\times \mathbb{R}$ .

Lemma 10. Suppose that $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ . Then, for $(t,x)\in \lbrack0,\Delta]\times \mathbb{R}$ ,

(22) \begin{equation} |u(t,x)-u_{\Delta}(t,x)|\leq C_{\phi}(M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}}, \end{equation}

where $C_{\phi}$ is the Lipschitz constant of $\phi$ , $M_{\xi}^{1}\;:\!=\;\tilde{\mathbb{E}}[|\xi|]$ and $M_{X}^{1}\;:\!=\;\hat{\mathbb{E}}[|X_{1}|]$ .

Proof. Clearly, (22) holds in $(t,x)\in \lbrack0,\Delta)\times \mathbb{R}$ , since $u(0,x)=u_{\Delta}(t,x)=\phi(x)$ , $(t,x)\in \lbrack0,\Delta)\times \mathbb{R}$ . For $t=\Delta$ , from Lemma 3 and (6), we obtain

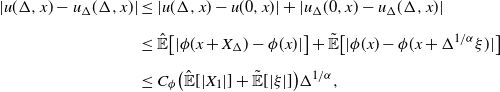\begin{align*} |u(\Delta,x)-u_{\Delta}(\Delta,x)| & \leq |u(\Delta,x)-u(0,x)| + |u_{\Delta}(0,x)-u_{\Delta}(\Delta,x)| \\[5pt] & \leq \hat{\mathbb{E}}\big[|\phi(x+X_{\Delta})-\phi(x)|\big] + \tilde{\mathbb{E}}\big[|\phi(x)-\phi(x+\Delta^{{1}/{\alpha}}\xi)|\big] \\[5pt] & \leq C_{\phi}\big(\hat{\mathbb{E}}[|X_{1}|]+\tilde{\mathbb{E}}[|\xi|]\big)\Delta^{{1}/{\alpha}}, \end{align*}

which implies the desired result.

5.3.1. Lower bound for the approximation scheme error

In order to obtain the lower bound for the approximation scheme, we follow Krylov’s regularization results [25–27] (see also [2, 3] for analogous results under PDE arguments). For $\varepsilon \in(0,1)$ , we first extend (3) to the domain $[0,T+\varepsilon^{2}]\times \mathbb{R}$ and still denote it as u. For $(t,x)\in \lbrack0,T]\times \mathbb{R}$ , we define the mollification of u by

\[ u^{\varepsilon}(t,x) = u\ast\zeta_{\varepsilon}(t,x) = \int_{-\varepsilon^{2}<\tau<0}\int_{|e|<\varepsilon}u(t-\tau,x-e)\zeta_{\varepsilon}(\tau,e)\,\textrm{d} e\,\textrm{d}\tau.\]

In view of Lemma 4, the standard properties of mollifiers indicate that

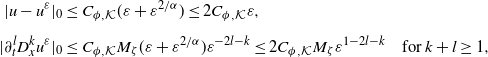(23) \begin{equation} \begin{aligned} |u-u^{\varepsilon}|_{0} & \leq C_{\phi,\mathcal{K}}(\varepsilon+\varepsilon^{{2}/{\alpha}}) \leq 2C_{\phi,\mathcal{K}}\varepsilon, \\[5pt] |\partial_{t}^{l}D_{x}^{k}u^{\varepsilon}|_{0} & \leq C_{\phi,\mathcal{K}}M_{\zeta}(\varepsilon+\varepsilon^{{2}/{\alpha}})\varepsilon^{-2l-k} \leq 2C_{\phi,\mathcal{K}}M_{\zeta}\varepsilon^{1-2l-k} \quad \text{for } k+l \geq 1, \end{aligned} \end{equation}

where $M_{\zeta}\;:\!=\;\max_{k+l\geq1}\int_{-1<t<0}\int_{|x|<1}|\partial_{t}^{l}D_{x}^{k}\zeta(t,x)|\,\textrm{d} x\,\textrm{d} t < \infty$ .

We obtain the following lower bound.

Lemma 11. Suppose that Assumptions 1–3 hold, and $\phi \in C_\textrm{b,Lip}(\mathbb{R})$ . Then, for $(t,x)\in \lbrack0,T]\times \mathbb{R}$ , $u_{\Delta}(t,x)\leq u(t,x)+L_{0}\Delta^{\Gamma(\alpha,q)}$ , where

\begin{equation*}\Gamma(\alpha,q)=\min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha},\frac{q}{2}\bigg\}\end{equation*}

and $L_{0}$ is a constant depending on $C_{\phi}$ , $C_{\phi,\mathcal{K}}$ , $M_{X}^{1}$ , $M_{\xi}^{1}$ , $M_{\zeta}$ , and M, and is given in (26).

Proof. Step 1. Notice that $u(t-\tau,x-e)$ is a viscosity solution of (3) in $[0,T]\times \mathbb{R}$ for any $(\tau,e)\in(\!-\varepsilon^{2},0)\times B(0,\varepsilon)$ . Multiplying it by $\zeta_{\varepsilon}(\tau,e)$ and integrating it with respect to $(\tau,e)$ , from the concavity of (3) with respect to the nonlocal term we can derive that $u^{\varepsilon}(t,x)$ is a supersolution of (3) in $(0,T]\times\mathbb{R}$ , i.e. for $(t,x)\in(0,T]\times \mathbb{R}$ ,

(24) \begin{equation} \partial_{t}u^{\varepsilon}(t,x) - \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}\delta_{z}u^{\varepsilon}(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} \geq 0. \end{equation}

Step 2. Since $u^{\varepsilon}\in C_\textrm{b}^{\infty}([0,T]\times \mathbb{R})$ , together with the consistency property in Proposition 2(iii) and (24), using (23), we can deduce that

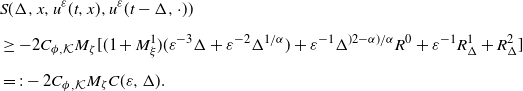(25) \begin{align} & S(\Delta,x,u^{\varepsilon}(t,x),u^{\varepsilon}(t-\Delta,\cdot)) \nonumber \\[5pt] & \geq -2C_{\phi,\mathcal{K}}M_{\zeta}[(1+M_{\xi}^{1})(\varepsilon^{-3}\Delta+\varepsilon^{-2}\Delta^{{1}/{\alpha}}) + \varepsilon^{-1}\Delta^{){2-\alpha})/{\alpha}}R^{0} + \varepsilon^{-1}R_{\Delta}^{1} + R_{\Delta}^{2}] \nonumber \\[5pt] & =:-2C_{\phi,\mathcal{K}}M_{\zeta}C(\varepsilon,\Delta). \end{align}

Applying the comparison principle in Lemma 9 to $u_{\Delta}$ and $u^{\varepsilon}$ , by (17) and (25), we have, for $(t,x)\in[0,T]\times\mathbb{R}$ ,

\begin{equation*} u_{\Delta}-u^{\varepsilon} \leq \sup_{(t,x)\in \lbrack0,\Delta]\times \mathbb{R}}(u_{\Delta}-u^{\varepsilon})^{+} + 2TC_{\phi,\mathcal{K}}M_{\zeta}C(\varepsilon,\Delta). \end{equation*}

Step 3. In view of the previous equation and Lemma 10, we obtain

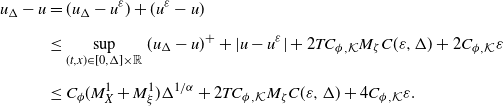\begin{align*} u_{\Delta}-u & = (u_{\Delta}-u^{\varepsilon})+(u^{\varepsilon}-u) \\[5pt] & \leq \sup_{(t,x)\in \lbrack0,\Delta]\times \mathbb{R}}(u_{\Delta}-u)^{+} + |u-u^{\varepsilon}| + 2TC_{\phi,\mathcal{K}}M_{\zeta}C(\varepsilon,\Delta) + 2C_{\phi,\mathcal{K}}\varepsilon \\[5pt] & \leq C_{\phi}(M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}} + 2TC_{\phi,\mathcal{K}}M_{\zeta}C(\varepsilon,\Delta) + 4C_{\phi,\mathcal{K}}\varepsilon. \end{align*}

Assumptions 1–3 indicate that $R^{0}\leq4M$ , $R_{\Delta}^{1}\leq10C\Delta^{q}$ , and $R_{\Delta}^{2}\leq16C\Delta^{q}$ . When $\alpha\in\big(1,\frac{4}{3}\big]$ and $q\in \big[\frac{1}{2},\infty\big)$ , by choosing $\varepsilon=\Delta^{{1}/{4}}$ we have $u_{\Delta}-u\leq L_{0}\Delta^{{1}/{4}}$ , where

(26) \begin{equation} L_{0} \;:\!=\; C_{\phi}(M_{X}^{1}+M_{\xi}^{1}) + 4C_{\phi,\mathcal{K}} + 2TC_{\phi,\mathcal{K}}M_{\zeta}[2(1+M_{\xi}^{1})+4M+26C]; \end{equation}

when $\alpha \in\big(1,\frac{4}{3}\big]$ and $q\in \big[0,\frac{1}{2})$ , by choosing $\varepsilon=\Delta^{{q}/{2}}$ , we have $u_{\Delta}-u\leq L_{0}\Delta^{{q}/{2}}$ ; when $\alpha\in\big(\frac{4}{3},2\big)$ and $q\in \lbrack({2-\alpha})/{\alpha},\infty)$ , by letting $\varepsilon=\Delta^{({2-\alpha})/{2\alpha}}$ we get $u_{\Delta}-u\leq L_{0}\Delta^{({2-\alpha})/{2\alpha}}$ ; when $\alpha\in\big(\frac{4}{3},2\big)$ and $q\in(0,({2-\alpha})/{\alpha})$ , by letting $\varepsilon=\Delta^{{q}/{2}}$ we get $u_{\Delta}-u\leq L_{0}\Delta^{{q}/{2}}$ . To sum up, we conclude that $u_{\Delta}-u\leq L_{0}\Delta^{\Gamma(\alpha,q)}$ , where

\begin{align*}\Gamma(\alpha,q)=\min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha},\frac{q}{2}\bigg\}.\end{align*}

This leads to the desired result.

5.3.2. Upper bound for the approximation scheme error

To obtain an upper bound for the approximation scheme error, we are not able to construct approximate smooth subsolutions of (3) due to the concavity of (3). Instead, we interchange the roles of the PIDE (3) and the approximation scheme (17). For $\varepsilon\in(0,1)$ , we extend (17) to the domain $[0,T+\varepsilon^{2}]\times \mathbb{R}$ and still denote it as $u_{\Delta}$ . For $(t,x)\in\lbrack0,T]\times \mathbb{R}$ , we define the mollification of u by

\[ u_{\Delta}^{\varepsilon}(t,x) = u_{\Delta}\ast\zeta_{\varepsilon}(t,x) = \int_{-\varepsilon^{2}<\tau<0}\int_{|e|<\varepsilon}u_{\Delta}(t-\tau,x-e)\zeta_{\varepsilon}(\tau,e)\,\textrm{d}\tau\,\textrm{d} e.\]

In view of Theorem 3, the standard properties of mollifiers indicate that

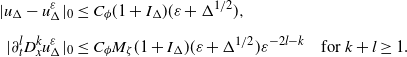(27) \begin{equation} \begin{aligned} |u_{\Delta}-u_{\Delta}^{\varepsilon}|_{0} & \leq C_{\phi}(1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}}), \\[5pt] |\partial_{t}^{l}D_{x}^{k}u_{\Delta}^{\varepsilon}|_{0} & \leq C_{\phi}M_{\zeta}(1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}})\varepsilon^{-2l-k} \quad \text{for } k+l \geq 1. \end{aligned} \end{equation}

We obtain the following upper bound.

Lemma 12. Suppose that Assumptions 1–3 hold and $\phi\in C_\textrm{b,Lip}(\mathbb{R})$ . Then, for $(t,x)\in \lbrack0,T]\times \mathbb{R}$ , $u(t,x)\leq u_{\Delta}(t,x)+U_{0}\Delta^{\Gamma(\alpha,q)}$ , where

\begin{align*}\Gamma(\alpha,q)=\min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha},\frac{q}{2}\bigg\}\end{align*}

and $U_{0}$ is a constant depending on $C_{\phi}$ , $C_{\phi,\mathcal{K}}$ , $M_{X}^{1}$ , $M_{\xi}^{1}$ , $M_{\zeta}$ , M, and $I_{\Delta}$ , and is given in (29).

Proof. Step 1. Note that for any $(t,x)\in[\Delta,T]\times \mathbb{R}$ and $(\tau,e)\in(\!-\varepsilon^{2},0)\times B(0,\varepsilon)$ ,

\[ S(\Delta,x,u_{\Delta}(t-\tau,x-e),u_{\Delta}(t-\Delta,\cdot-e))=0. \]

Multiplying the above equality by $\zeta_{\varepsilon}(\tau,e)$ and integrating with respect to $(\tau,e)$ , from the concavity of the approximation scheme (17), we have, for $(t,x)\in(\Delta,T]\times\mathbb{R}$ ,

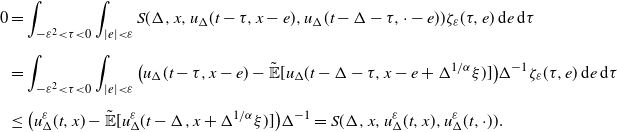(28) \begin{align} 0 & = \int_{-\varepsilon^{2}<\tau<0}\int_{|e|<\varepsilon}S(\Delta,x,u_{\Delta}(t-\tau,x-e), u_{\Delta}(t-\Delta-\tau,\cdot-e))\zeta_{\varepsilon}(\tau,e)\,\textrm{d} e\,\textrm{d}\tau \nonumber \\[5pt] & = \int_{-\varepsilon^{2}<\tau<0}\int_{|e|<\varepsilon} \big(u_{\Delta}(t-\tau,x-e)-\tilde{\mathbb{E}}[u_{\Delta}(t-\Delta-\tau,x-e+\Delta^{1/\alpha}\xi)]\big) \Delta^{-1}\zeta_{\varepsilon}(\tau,e)\,\textrm{d} e\,\textrm{d}\tau \nonumber \\[5pt] & \leq \big(u_{\Delta}^{\varepsilon}(t,x) - \tilde{\mathbb{E}}[u_{\Delta}^{\varepsilon}(t-\Delta,x+\Delta^{1/\alpha}\xi)]\big)\Delta^{-1} = S(\Delta,x,u_{\Delta}^{\varepsilon}(t,x),u_{\Delta}^{\varepsilon}(t,\cdot)). \end{align}

Step 2. Since $u_{\Delta}^{\varepsilon}\in C_{b}^{\infty}([0,T]\times\mathbb{R})$ , by substituting $u_{\Delta}^{\varepsilon}$ into the consistency property in Proposition 2(iii), together with (27) and (28), we can compute that

\[ \partial_{t}u_{\Delta}^{\varepsilon}(t,x) - \sup_{k_{\pm}\in K_{\pm}}\bigg\{\int_{\mathbb{R}}\delta_{z}u_{\Delta}^{\varepsilon}(t,x)F_{k_{\pm}}(\textrm{d} z)\bigg\} \geq -C_{\phi}M_{\zeta}(1+I_{\Delta})(1+\varepsilon^{-1}\Delta^{{1}/{2}})C(\varepsilon,\Delta), \]

where $C(\varepsilon,\Delta)$ is defined in (25). Then, the function

\[ \bar{v}(t,x) \;:\!=\; u_{\Delta}^{\varepsilon}(t,x) + C_{\phi}M_{\zeta}(1+I_{\Delta})(1+\varepsilon^{-1}\Delta^{{1}/{2}})C(\varepsilon,\Delta)(t-\Delta) \]

is a supersolution of (3) in $(\Delta,T]\times \mathbb{R}$ with initial condition $\bar{v}(\Delta,x)=u_{\Delta}^{\varepsilon}(\Delta,x)$ . In addition,

\[ \underline{v}(t,x) = u(t,x)- C_{\phi}(M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}} - C_{\phi}(1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}}) \]

is a viscosity solution of (3) in $(\Delta,T]\times \mathbb{R}$ . From (27) and Lemma 10, we can further obtain

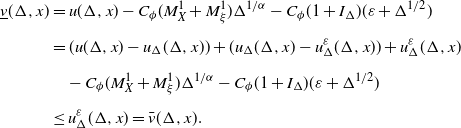\begin{align*} \underline{v}(\Delta,x) & = u(\Delta,x) - C_{\phi}(M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}} - C_{\phi}(1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}}) \\[5pt] & = (u(\Delta,x)-u_{\Delta}(\Delta,x)) + (u_{\Delta}(\Delta,x)-u_{\Delta}^{\varepsilon}(\Delta,x)) + u_{\Delta}^{\varepsilon}(\Delta,x) \\[5pt] & \quad - C_{\phi}(M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}} - C_{\phi}(1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}}) \\[5pt] & \leq u_{\Delta}^{\varepsilon}(\Delta,x) = \bar{v}(\Delta,x). \end{align*}

By means of the comparison principle for PIDE (3) (see [29, Proposition 5.5]), we conclude that $\underline{v}(t,x)\leq \bar{v}(t,x)$ in $[\Delta,T]\times \mathbb{R}$ , which implies, for $(t,x)\in \lbrack\Delta,T]\times \mathbb{R}$ ,

\begin{equation*} u-u_{\Delta}^{\varepsilon} \leq C_{\phi}\big[ (M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}} + (1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}}) + TM_{\zeta}(1+I_{\Delta})(1+\varepsilon^{-1}\Delta^{{1}/{2}})C(\varepsilon,\Delta)\big]. \end{equation*}

Step 3. Using the previous equation and (27), we have

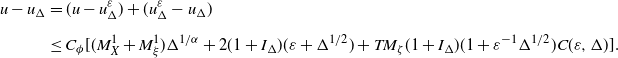\begin{align*} u-u_{\Delta} & = (u-u_{\Delta}^{\varepsilon}) + (u_{\Delta}^{\varepsilon}-u_{\Delta}) \\[5pt] & \leq C_{\phi}[(M_{X}^{1}+M_{\xi}^{1})\Delta^{{1}/{\alpha}} + 2(1+I_{\Delta})(\varepsilon+\Delta^{{1}/{2}}) + TM_{\zeta}(1+I_{\Delta})(1+\varepsilon^{-1}\Delta^{{1}/{2}})C(\varepsilon,\Delta)]. \end{align*}

Under Assumptions 1–3, we have $I_{\Delta}<\infty$ , $R^{0}\leq4M$ , $R_{\Delta}^{1}\leq10C\Delta^{q}$ , and $R_{\Delta}^{2}\leq16C\Delta^{q}$ . In the same way as for Lemma 11, by minimizing with respect to $\varepsilon$ we can derive that, for $(t,x)\in \lbrack \Delta,T]\times\mathbb{R}$ , $u-u_{\Delta}\leq U_{0}\Delta^{\Gamma(\alpha,q)}$ , where

(29) \begin{equation} U_{0} = C_{\phi}[M_{X}^{1}+M_{\xi}^{1}+4(1+I_{\Delta})+2TM_{\zeta}(1+I_{\Delta})(2(1+M_{\xi}^{1})+4M+26C)] \end{equation}

and

\begin{align*}\Gamma(\alpha,q)=\min\bigg\{\frac{1}{4},\frac{2-\alpha}{2\alpha},\frac{q}{2}\bigg\}.\end{align*}

Combining this and Lemma 10, we obtain the desired result.