Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Strawderman, William E.
and
Holmes, Paul T.
1970.
On the law of the iterated logarithm for inter-record times.
Journal of Applied Probability,
Vol. 7,
Issue. 2,
p.
432.
Shorrock, R. W.
1972.
A limit theorem for inter-record times.
Journal of Applied Probability,
Vol. 9,
Issue. 01,
p.
219.
Barr, Donald R.
1972.
When Will the Next Record Rainfall Occur?.
Mathematics Magazine,
Vol. 45,
Issue. 1,
p.
15.
Resnick, Sidney I.
1973.
Extremal processes and record value times.
Journal of Applied Probability,
Vol. 10,
Issue. 4,
p.
864.
Resnick, Sidney I.
1973.
Extremal processes and record value times.
Journal of Applied Probability,
Vol. 10,
Issue. 4,
p.
864.
Resnick, Sidney I.
and
Rubinovitch, Michael
1973.
The structure of extremal processes.
Advances in Applied Probability,
Vol. 5,
Issue. 2,
p.
287.
Biondini, Ronald
and
Siddiqui, M.M.
1975.
Statistical Inference and Related Topics.
p.
291.
Yang, Mark C. K.
1975.
On the distribution of the inter-record times in an increasing population.
Journal of Applied Probability,
Vol. 12,
Issue. 01,
p.
148.
Lee Guthrie, Gary
and
Holmes, Paul T.
1975.
On record and inter-record times for a sequence of random variables defined on a Markov chain.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
195.
Glick, Ned
1978.
Breaking Records and Breaking Boards.
The American Mathematical Monthly,
Vol. 85,
Issue. 1,
p.
2.
1980.
Martingale Limit Theory and its Application.
p.
285.
Nayak, S.S.
1984.
Almost sure limit points of and the number of boundary crossings related to SLLN and LIL for record times, inter-record times and the number of record values.
Stochastic Processes and their Applications,
Vol. 17,
Issue. 1,
p.
167.
Nevzorov, V. B.
1988.
Records.
Theory of Probability & Its Applications,
Vol. 32,
Issue. 2,
p.
201.
Imlahi, A.
1995.
Functional laws of the iterated logarithm for records.
Journal of Statistical Planning and Inference,
Vol. 45,
Issue. 1-2,
p.
215.
Nevzorov, Valery B.
and
Balakrishnan, N.
1998.
Order Statistics: Theory & Methods.
Vol. 16,
Issue. ,
p.
515.
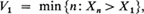 and for r ≧ 1,
and for r ≧ 1,
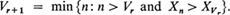 Vr is the trial on which the rth (upper) record observation occurs. {Vr} will be an infinite sequence of random variables since the underlying distribution function of the X's is continuous. It is well known that the expected value of Vr. is infinite for every r (see, for example, Feller [1], page 15). Also define
Vr is the trial on which the rth (upper) record observation occurs. {Vr} will be an infinite sequence of random variables since the underlying distribution function of the X's is continuous. It is well known that the expected value of Vr. is infinite for every r (see, for example, Feller [1], page 15). Also define
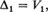 and for r > 1
and for r > 1
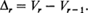 δr is the number of trials between the (r - l)th and the rth record. The distributions of the random variables Vr and δr do not depend on the distribution of the original random variables. It can be shown (see Neuts [2], page 206 or Tata 1[4], page 26) that
δr is the number of trials between the (r - l)th and the rth record. The distributions of the random variables Vr and δr do not depend on the distribution of the original random variables. It can be shown (see Neuts [2], page 206 or Tata 1[4], page 26) that
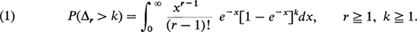 The following theorem is due to Neuts [2].
The following theorem is due to Neuts [2].

