Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T22:53:23.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Fonctions Certaines Admettant des Répartitions Asymptotiques et Fonctions Aléatoires Stationnaires

Published online by Cambridge University Press:  05 September 2017

A. Blanc-Lapierre
Get access Rights & Permissions [Opens in a new window]

Abstract

In the article below, we consider sets of non-random functions of time t admitting certain asymptotic distributions. Purely temporal and deterministic considerations lead us to associate to a set 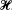, say, of functions H(t) of this type, a space Ω of samples ω.

To each function H(t) ⊂ 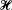, there corresponds a random variable h (ω). To the set of translated functions H(t + λ) of a function H(t) ⊂ 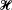, there corresponds a stationary random function of the translation parameter λ, say, h(λ, ω). We study the transposition to the set of non-random functions H(t) of such properties as moments, gaussian character, independence, harmonic analysis, and others, of the random variables h (ω) and of the random functions h (λ, ω).

Some remarks are made concerning the links between ergodicity and the above problems.

Type
Part V — Stochastic Processes
Information
Journal of Applied Probability , Volume 12 , Issue S1 , 1975 , pp. 177 - 185
Copyright
Copyright © 1975 Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

[1] Kac, M. (1936) Sur les fonctions indépendantes I. Studia Math. 6, 45–58.Google Scholar
Steinhaus, H. Et (1936) Sur les fonctions indépendantes II. Studia Math. 6, 59–66.Google Scholar
Steinhaus, H. (1938) La théorie et les applications des fonctions indépendantes au sens stochastique. Actualités Sci. Indust. 738, 57–73.Google Scholar
[2] Wiener, N. (1930) Generalized harmonic analysis. Acta Math. 55, 117, 258.Google Scholar
[3] Bertrandias, J. P. (1964) Espaces de fonctions bornées et continues en moyenne asymptotique d'ordre p. Thèse, Université de Paris.Google Scholar
[4] Blanc-Lapierre, A. Et Lefèvre, C. (1972) Analyse harmonique généralisée et fonctions aléatoires stationnaires. C. R. Acad. Sci. Paris Sér. A 274, 257–261.Google Scholar
[5] Pham, P. H. (1968) Fonctions admettant une répartition asymptotique des valeurs. C. R. Acad. Sci. Paris Sér. A 267, 803.Google Scholar
Pham, P. H. (1969) Deux théorèmes sur les mesures asymptotiques. C. R. Acad. Sci. Paris Sér. A 268, 448.Google Scholar
Pham, P. H. (1972) Mesures asymptotiques. Thèse, Université de Paris.Google Scholar
[6] Loeve, M. (1962) Probability Theory. 3ème edition. D. Van Nostrand Company, New York.Google Scholar
[7] Blanc-Lapierre, A. Et Fortet, R. (1953) Théorie des fonctions aléatoires. Masson et Cie, Paris.Google Scholar
[8] Blanc-Lapierre, À. Et Lefevre, C. (1972) Sur quelques propriétés de moments d'ordres supérieurs intervenant dans l'étude de la stabilité de certains systèmes bouclés. C. R. Acad. Sci. Paris Sér. A 274, 1266–1270.Google Scholar