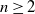1. Introduction
Percolation theory is a fascinating area of modern probability, which tries to understand under which conditions infinite components arise in random structures. In the present article, we study the properties of a Boolean percolation model on directed graphs and relate this model to a classical Markov chain known as the random exchange process.
Let
![]() $\mathcal{G} = (V,E)$
be a directed graph with an infinite, countable vertex set V. For all vertices x,
$\mathcal{G} = (V,E)$
be a directed graph with an infinite, countable vertex set V. For all vertices x,
![]() $y \in V$
, we let
$y \in V$
, we let
![]() $d(x,y) \in \mathbb{N}_0 \cup \{ \infty \}$
denote the distance from x to y in
$d(x,y) \in \mathbb{N}_0 \cup \{ \infty \}$
denote the distance from x to y in
![]() $\mathcal{G}$
. Note that
$\mathcal{G}$
. Note that
![]() $d\,:\, V \times V \rightarrow \mathbb{N}_0 \cup \{ \infty \}$
is an extended quasimetric on V, which is symmetric if and only if the graph
$d\,:\, V \times V \rightarrow \mathbb{N}_0 \cup \{ \infty \}$
is an extended quasimetric on V, which is symmetric if and only if the graph
![]() $\mathcal{G}$
is undirected, i.e.
$\mathcal{G}$
is undirected, i.e.
![]() $(x,y) \in E$
implies
$(x,y) \in E$
implies
![]() $(y,x) \in E$
for all x,
$(y,x) \in E$
for all x,
![]() $y \in V$
. Moreover, for all
$y \in V$
. Moreover, for all
![]() $x \in V$
and
$x \in V$
and
![]() $n \in \mathbb{N}_0$
, we let
$n \in \mathbb{N}_0$
, we let
![]() $B_n (x)$
denote the open ball of radius n starting from x, which is the set of all vertices
$B_n (x)$
denote the open ball of radius n starting from x, which is the set of all vertices
![]() $y \in V$
with
$y \in V$
with
![]() $d(x,y) < n$
. So,
$d(x,y) < n$
. So,
![]() $B_0 (x) = \emptyset$
and
$B_0 (x) = \emptyset$
and
![]() $B_1 ( x) = \{ x \}$
for all
$B_1 ( x) = \{ x \}$
for all
![]() $x \in V$
.
$x \in V$
.
Let
![]() $\mu = (\mu_n)_{n \in \mathbb{N}_0}$
be a probability vector and let
$\mu = (\mu_n)_{n \in \mathbb{N}_0}$
be a probability vector and let
![]() $(Y_x)_{x \in V}$
be a family of independent and identically distributed (i.i.d.) random variables satisfying
$(Y_x)_{x \in V}$
be a family of independent and identically distributed (i.i.d.) random variables satisfying
![]() $\mathbb{P}[ Y_x = n] = \mu_n$
for all
$\mathbb{P}[ Y_x = n] = \mu_n$
for all
![]() $n \geq 0$
. In our percolation model, for all
$n \geq 0$
. In our percolation model, for all
![]() $x \in V$
, the random variable
$x \in V$
, the random variable
![]() $Y_x$
represents the coverage radius of the vertex x. Hence the set of covered, respectively uncovered, vertices are
$Y_x$
represents the coverage radius of the vertex x. Hence the set of covered, respectively uncovered, vertices are
Note that if
![]() $\mu_0 + \mu_1 = 1$
, this Boolean percolation model reduces to Bernoulli percolation on the sites of the graph
$\mu_0 + \mu_1 = 1$
, this Boolean percolation model reduces to Bernoulli percolation on the sites of the graph
![]() $\mathcal{G}$
, as every vertex may only cover itself.
$\mathcal{G}$
, as every vertex may only cover itself.
As we are interested in the properties of the random sets
![]() $V_\mu$
and
$V_\mu$
and
![]() $V_\mu^c$
, we will always assume
$V_\mu^c$
, we will always assume
![]() $\mu_0 \in (0,1)$
, since
$\mu_0 \in (0,1)$
, since
![]() $V_\mu = V$
almost surely in the case of
$V_\mu = V$
almost surely in the case of
![]() $\mu_0=0$
, and
$\mu_0=0$
, and
![]() $V_\mu = \emptyset$
almost surely for
$V_\mu = \emptyset$
almost surely for
![]() $\mu_0=1$
. Moreover, in our study we will assume that
$\mu_0=1$
. Moreover, in our study we will assume that
![]() $\mathcal{G}$
is weakly connected.
$\mathcal{G}$
is weakly connected.
Let x,
![]() $y \in V$
and
$y \in V$
and
![]() $V^{\prime} = V_\mu$
or
$V^{\prime} = V_\mu$
or
![]() $V^{\prime}= V_\mu^c$
. Then, if both x and y are contained in V
′ and connected by a path in
$V^{\prime}= V_\mu^c$
. Then, if both x and y are contained in V
′ and connected by a path in
![]() $\mathcal{G}$
, which uses only vertices from V
′, we will say that x and y are in the same cluster.
$\mathcal{G}$
, which uses only vertices from V
′, we will say that x and y are in the same cluster.
To state our results, we introduce the following notation. Let
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $V = \mathbb{N}_0^n$
, or
$V = \mathbb{N}_0^n$
, or
![]() $ V = \mathbb{Z}^n$
(see Figure 1), and E be the set of all pairs
$ V = \mathbb{Z}^n$
(see Figure 1), and E be the set of all pairs
![]() $(x,x+e_j)$
, where
$(x,x+e_j)$
, where
![]() $x \in V$
,
$x \in V$
,
![]() $j=1,\ldots,n$
, and
$j=1,\ldots,n$
, and
![]() $e_j = (\delta_{ij})_{i=1,\ldots,n}$
. Then we denote the resulting graph
$e_j = (\delta_{ij})_{i=1,\ldots,n}$
. Then we denote the resulting graph
![]() $\mathcal{G} = (V,E)$
by
$\mathcal{G} = (V,E)$
by
![]() $\mathbb{N}_0^n$
, respectively
$\mathbb{N}_0^n$
, respectively
![]() $\mathbb{Z}^n$
. Furthermore, for all
$\mathbb{Z}^n$
. Furthermore, for all
![]() $n \geq 2$
, we define the infinite directed n-ary tree
$n \geq 2$
, we define the infinite directed n-ary tree
![]() $\mathcal{D}_n \,:\!=\, (V_n, E_n)$
by
$\mathcal{D}_n \,:\!=\, (V_n, E_n)$
by
 \begin{align*}V_n &\,:\!=\, \bigcup_{m \geq 0} \{ 1,\ldots,n \}^m, \quad \text{where $ \{ 1,\ldots,n \}^0 \,:\!=\, \emptyset$,}\\E_n &\,:\!=\, \{ (\emptyset , 1 ),\ldots, ( \emptyset, n ) \} \cup \{ ( x, (x,j) ) \mid x \in V_n \setminus \{ \emptyset \}, \ j=1,\ldots,n \}.\end{align*}
\begin{align*}V_n &\,:\!=\, \bigcup_{m \geq 0} \{ 1,\ldots,n \}^m, \quad \text{where $ \{ 1,\ldots,n \}^0 \,:\!=\, \emptyset$,}\\E_n &\,:\!=\, \{ (\emptyset , 1 ),\ldots, ( \emptyset, n ) \} \cup \{ ( x, (x,j) ) \mid x \in V_n \setminus \{ \emptyset \}, \ j=1,\ldots,n \}.\end{align*}

Figure 1. Illustration of the lattices
![]() $\mathbb{N}_0^2$
(a) and
$\mathbb{N}_0^2$
(a) and
![]() $\mathbb{Z}^2$
(b).
$\mathbb{Z}^2$
(b).
In this article we will clarify under which conditions the graphs
![]() $\mathbb{N}_0^n$
and
$\mathbb{N}_0^n$
and
![]() $\mathbb{Z}^n$
are (essentially) covered by a distribution
$\mathbb{Z}^n$
are (essentially) covered by a distribution
![]() $\mu$
; see Theorems 1 and 2 below. On the other hand, in Theorem 3, we will see that for any distribution
$\mu$
; see Theorems 1 and 2 below. On the other hand, in Theorem 3, we will see that for any distribution
![]() $\mu$
and
$\mu$
and
![]() $n \geq 2$
,
$n \geq 2$
,
![]() $\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely.
$\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely.
To the best of our knowledge, the present percolation model was first studied by Lamperti [Reference Lamperti27] for
![]() $\mathcal{G} = \mathbb{N}_0$
. This research was motivated by statistical physics and included the following description. At each location
$\mathcal{G} = \mathbb{N}_0$
. This research was motivated by statistical physics and included the following description. At each location
![]() $n \in \mathbb{N}_0$
there is a fountain, which sprays water to the right and is wetting the segment from
$n \in \mathbb{N}_0$
there is a fountain, which sprays water to the right and is wetting the segment from
![]() $n+1$
to
$n+1$
to
![]() $n+ Y_n$
. As
$n+ Y_n$
. As
![]() $\mu_0> 0$
, with some positive probability, a fountain fails to operate at all.
$\mu_0> 0$
, with some positive probability, a fountain fails to operate at all.
Our percolation model and variants of it have been studied by various authors; see [Reference Bertacchi and Zucca6], [Reference Gallo, Garcia, Junior and Rodrguez15], [Reference Junior, Machado and Ravishankar23], [Reference Junior, Machado and Zuluaga24], [Reference Junior, Machado and Zuluaga25], and [Reference Lebensztayn and Rodríguez29]. For a recent survey, see [Reference Junior, Machado and Ravishankar23]. At this point, however, we want to postpone the discussion of how our new insights and results are related to these articles.
We can interpret our percolation model as the spread of a rumour through a network, a firework process, or a discrete version of Boolean percolation. The latter model was introduced by Gilbert [Reference Gilbert17]. First, points are chosen randomly in
![]() $\mathbb{R}^n$
according to a Poisson point process. Then, in the simplest case, around these points, the unit sphere is covered. For monographs concerned with Boolean percolation, see [Reference Hall19], [Reference Meester and Roy30], [Reference Schneider and Weil33], and [Reference Stoyan, Kendall and Mecke34].
$\mathbb{R}^n$
according to a Poisson point process. Then, in the simplest case, around these points, the unit sphere is covered. For monographs concerned with Boolean percolation, see [Reference Hall19], [Reference Meester and Roy30], [Reference Schneider and Weil33], and [Reference Stoyan, Kendall and Mecke34].
We also want to mention that the discrete percolation model of the present paper was used by Bezborodov and Krueger [Reference Bezborodov and Krueger8] to study the growth of continuous-time frog processes.
Apart from our Boolean percolation itself, we also investigate its connection to a rather classical Markov chain, which is sometimes called random exchange process. As far as we know, it was first observed by Zerner [Reference Zerner36, Section 1] that these two stochastic models are related to each other.
Let
![]() $(Y_n)_{n \geq 0}$
denote a sequence of i.i.d. random variables, which, as before, are distributed according to
$(Y_n)_{n \geq 0}$
denote a sequence of i.i.d. random variables, which, as before, are distributed according to
![]() $\mu$
. Then we set
$\mu$
. Then we set
![]() $X_0 \,:\!=\, Y_0$
and recursively define
$X_0 \,:\!=\, Y_0$
and recursively define
To the best of our knowledge, this process
![]() $(X_n)_{n \geq 0}$
first occurred in a statistical research article on deepwater exchange of a fjord; see [Reference Gade14]. It was later studied in a more general form in [Reference Helland20] and [Reference Helland and Nilsen21]. In the following, we call the Markov chain
$(X_n)_{n \geq 0}$
first occurred in a statistical research article on deepwater exchange of a fjord; see [Reference Gade14]. It was later studied in a more general form in [Reference Helland20] and [Reference Helland and Nilsen21]. In the following, we call the Markov chain
![]() $(X_n)_{n \geq 0}$
a (constant decrement) random exchange process. By construction, it has time-homogeneous transition probabilities and is irreducible on its state space
$(X_n)_{n \geq 0}$
a (constant decrement) random exchange process. By construction, it has time-homogeneous transition probabilities and is irreducible on its state space
![]() $\mathcal{X}$
, which is equal to
$\mathcal{X}$
, which is equal to
![]() $\mathbb{N}_0$
if
$\mathbb{N}_0$
if
![]() $\mu$
is unbounded, and otherwise takes the form
$\mu$
is unbounded, and otherwise takes the form
![]() $\{ 0, 1, \ldots, n_0 \}$
, where
$\{ 0, 1, \ldots, n_0 \}$
, where
![]() $n_0 \,:\!=\, \sup \{n \in \mathbb{N}\mid \mu_n \neq 0 \}$
. The transition matrix P associated with
$n_0 \,:\!=\, \sup \{n \in \mathbb{N}\mid \mu_n \neq 0 \}$
. The transition matrix P associated with
![]() $(X_n)_{n \geq 0}$
is
$(X_n)_{n \geq 0}$
is
 \[P \,:\!=\, P_\mu \,:\!=\, ( P_{\mu; x,y} )_{x,y \in \mathcal{X}}, \quad \text{where}\ P_{\mu; x,y} \,:\!=\, \begin{cases}\mu_y,&y \geq x,\\\sum_{z=0}^{x-1} \mu_z, & y = x-1,\\0,& y \leq x - 2. \\\end{cases}\]
\[P \,:\!=\, P_\mu \,:\!=\, ( P_{\mu; x,y} )_{x,y \in \mathcal{X}}, \quad \text{where}\ P_{\mu; x,y} \,:\!=\, \begin{cases}\mu_y,&y \geq x,\\\sum_{z=0}^{x-1} \mu_z, & y = x-1,\\0,& y \leq x - 2. \\\end{cases}\]
As
![]() $(X_n)_{n \geq 0}$
, respectively P, is irreducible, for all
$(X_n)_{n \geq 0}$
, respectively P, is irreducible, for all
![]() $z>0$
, the Green’s function
$z>0$
, the Green’s function
either converges or diverges simultaneously for all x,
![]() $y \in \mathcal{X}$
; see [Reference Woess35, Chapter 1.1]. Therefore, independent of the choice of x,
$y \in \mathcal{X}$
; see [Reference Woess35, Chapter 1.1]. Therefore, independent of the choice of x,
![]() $y \in \mathcal{X}$
, we can define the spectral radius of
$y \in \mathcal{X}$
, we can define the spectral radius of
![]() $(X_n)_{n \geq 0}$
, respectively P, by
$(X_n)_{n \geq 0}$
, respectively P, by
More generally, if A is an arbitrary irreducible matrix with non-negative entries, we can define
![]() $\rho(A) \in [0,\infty]$
in exactly the same way.
$\rho(A) \in [0,\infty]$
in exactly the same way.
Let us now state connections between the set
![]() $V_\mu$
of covered vertices in our percolation model and the Markov chain
$V_\mu$
of covered vertices in our percolation model and the Markov chain
![]() $(X_n)_{n \geq 0}$
. We start by reformulating previous results as follows.
$(X_n)_{n \geq 0}$
. We start by reformulating previous results as follows.
Theorem 1.
For any law
![]() $\mu$
, the following statements are equivalent.
$\mu$
, the following statements are equivalent.
-
(i) Almost surely,
 $\# V_\mu^c ( \mathbb{Z}) < \infty$
.
$\# V_\mu^c ( \mathbb{Z}) < \infty$
. -
(ii) Almost surely,
 $V_\mu ( \mathbb{Z}) = \mathbb{Z}$
.
$V_\mu ( \mathbb{Z}) = \mathbb{Z}$
. -
(iii) The Markov chain
 $(X_n)_{n \geq 0}$
is not positive recurrent.
$(X_n)_{n \geq 0}$
is not positive recurrent.
-
(iv) The expectation of
 $\mu$
is infinite, i.e.
$\mu$
is infinite, i.e.
 $\sum_{n \geq 0} n \mu_n = \infty$
.
$\sum_{n \geq 0} n \mu_n = \infty$
.
It is not difficult to verify, more generally, that (i) and (ii) are equivalent if we replace
![]() $\mathbb{Z}$
with an arbitrary vertex-transitive graph.
$\mathbb{Z}$
with an arbitrary vertex-transitive graph.
By applying the Borel–Cantelli lemma, we can directly verify that (ii) and (iv) are equivalent statements. This equivalence was also observed, in a more general form, in [Reference Junior, Machado and Zuluaga24, Section 2.2] and [Reference Bertacchi and Zucca6, Section 4]. For any graph
![]() $\mathcal{G}=(V,E)$
, we have
$\mathcal{G}=(V,E)$
, we have
![]() $V_\mu = V$
almost surely if and only if
$V_\mu = V$
almost surely if and only if
For example, for all
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $V_\mu ( \mathbb{Z}^n )= \mathbb{Z}^n$
almost surely if and only if the nth moment of
$V_\mu ( \mathbb{Z}^n )= \mathbb{Z}^n$
almost surely if and only if the nth moment of
![]() $\mu$
diverges. This kind of phenomenon is well known in the context of Boolean percolation models, and thus it seems convenient to include some previous literature results at this point.
$\mu$
diverges. This kind of phenomenon is well known in the context of Boolean percolation models, and thus it seems convenient to include some previous literature results at this point.
Hall [Reference Hall19] studied Boolean percolation on
![]() $\mathbb{R}^n$
with spheres of random i.i.d. radii and proved [Reference Hall19, Theorem 3.1] that the entire space is almost surely covered if and only if the nth moment of the radius distribution diverges. Gour [Reference Gouéré18] established that if the nth moment of the radius distribution is finite, there exists a critical value for the intensity of the underlying Poisson process. Recently, more results on phase transitions were deduced in [Reference Ahlberg, Tassion and Teixeira2] and [Reference Duminil-Copin and Raoufi13]. However, there are also results on other aspects of Boolean percolation. For example, Ahlberg et al. [Reference Ahlberg, Broman, Griffiths and Morris1] showed that this model is noise-sensitive, and Last et al. [Reference Last, Penrose and Zuyev28] studied the capacity functional.
$\mathbb{R}^n$
with spheres of random i.i.d. radii and proved [Reference Hall19, Theorem 3.1] that the entire space is almost surely covered if and only if the nth moment of the radius distribution diverges. Gour [Reference Gouéré18] established that if the nth moment of the radius distribution is finite, there exists a critical value for the intensity of the underlying Poisson process. Recently, more results on phase transitions were deduced in [Reference Ahlberg, Tassion and Teixeira2] and [Reference Duminil-Copin and Raoufi13]. However, there are also results on other aspects of Boolean percolation. For example, Ahlberg et al. [Reference Ahlberg, Broman, Griffiths and Morris1] showed that this model is noise-sensitive, and Last et al. [Reference Last, Penrose and Zuyev28] studied the capacity functional.
Athreya et al. [Reference Athreya, Roy and Sarkar3] and Bezborodov [Reference Bezborodov7] studied Boolean percolation on
![]() $[0,\infty)^n$
when, instead of the sphere around a point x, the set
$[0,\infty)^n$
when, instead of the sphere around a point x, the set
![]() $x + [0,R_x)^d$
is occupied, where
$x + [0,R_x)^d$
is occupied, where
![]() $R_x$
is the radius associated with x. The results in [Reference Athreya, Roy and Sarkar3] characterize under which conditions the entire space is essentially covered, and interestingly depend on whether
$R_x$
is the radius associated with x. The results in [Reference Athreya, Roy and Sarkar3] characterize under which conditions the entire space is essentially covered, and interestingly depend on whether
![]() $n=1$
or
$n=1$
or
![]() $n \geq 2$
. Bezborodov [Reference Bezborodov7] observed, for
$n \geq 2$
. Bezborodov [Reference Bezborodov7] observed, for
![]() $n=1$
and some radius distributions, that the covered volume fraction is one, but all clusters are bounded almost surely.
$n=1$
and some radius distributions, that the covered volume fraction is one, but all clusters are bounded almost surely.
Coletti and Grynberg [Reference Coletti and Grynberg11] studied a model on
![]() $\mathbb{Z}^n$
in which first Bernoulli percolation with parameter
$\mathbb{Z}^n$
in which first Bernoulli percolation with parameter
![]() $p \in (0,1)$
is performed, and then, independently around the present points, random i.i.d. balls are covered. Again, the occupied region is almost surely
$p \in (0,1)$
is performed, and then, independently around the present points, random i.i.d. balls are covered. Again, the occupied region is almost surely
![]() $\mathbb{Z}^n$
if and only if the nth moment of the radius distribution diverges. For a study of this percolation model on doubling graphs, see also [Reference Coletti, Miranda and Grynberg12].
$\mathbb{Z}^n$
if and only if the nth moment of the radius distribution diverges. For a study of this percolation model on doubling graphs, see also [Reference Coletti, Miranda and Grynberg12].
Let us return to Theorem 1. The equivalence of (iii) and (iv) was first observed by Helland [Reference Helland20, Section 3] and also mentioned by Kellerer [Reference Kellerer26, comments after Theorem 2.6]. We can deduce it as follows. Due to the form of the transition probabilities of the Markov chain
![]() $(X_n)_{n \geq 0}$
, any invariant measure
$(X_n)_{n \geq 0}$
, any invariant measure
![]() $\tau = (\tau_x)_{x \in \mathcal{X}}$
has to satisfy
$\tau = (\tau_x)_{x \in \mathcal{X}}$
has to satisfy
 \[\tau_{x} = \sum_{z \in \mathcal{X}} \tau_z P_{\mu;z,x} = \sum_{z=0}^x \tau_z \mu_x + \tau_{x+1} \sum_{z= 0}^{x} \mu_z, \quad \text{provided that $x, x+1 \in \mathcal{X}$,}\]
\[\tau_{x} = \sum_{z \in \mathcal{X}} \tau_z P_{\mu;z,x} = \sum_{z=0}^x \tau_z \mu_x + \tau_{x+1} \sum_{z= 0}^{x} \mu_z, \quad \text{provided that $x, x+1 \in \mathcal{X}$,}\]
or respectively
 \begin{align*}\tau_{x+1} = \Biggl( (1 - \mu_x) \tau_x - \sum_{z=0}^{x-1} \mu_x \tau_{z} \Biggr) \Bigg/ \Biggl( \sum_{z=0}^{x} \mu_z \Biggr).\end{align*}
\begin{align*}\tau_{x+1} = \Biggl( (1 - \mu_x) \tau_x - \sum_{z=0}^{x-1} \mu_x \tau_{z} \Biggr) \Bigg/ \Biggl( \sum_{z=0}^{x} \mu_z \Biggr).\end{align*}
We obtain
![]() $\tau_1 = \tau_0 (1 - \mu_0 ) \mu_0^{-1}$
,
$\tau_1 = \tau_0 (1 - \mu_0 ) \mu_0^{-1}$
,
and more generally the representation
 \begin{equation}\tau_x = \tau_0 \Biggl( \sum_{z \geq x} \mu_z \Biggr) \Biggl( \prod_{y=0}^{x-1} \sum_{z=0}^y \mu_z \Biggr)^{-1}, \quad x \in \mathcal{X}.\end{equation}
\begin{equation}\tau_x = \tau_0 \Biggl( \sum_{z \geq x} \mu_z \Biggr) \Biggl( \prod_{y=0}^{x-1} \sum_{z=0}^y \mu_z \Biggr)^{-1}, \quad x \in \mathcal{X}.\end{equation}
Indeed, from a careful look at this formula, it follows that (iii) and (iv) are equivalent. Moreover, if the distribution
![]() $\mu$
has a finite expectation, we can determine the stationary solution of
$\mu$
has a finite expectation, we can determine the stationary solution of
![]() $(X_n)_{n \geq 0}$
from (1) via normalization. In Section 3 we will present some concrete examples, and we also want to mention that results on positive recurrence of more general exchange processes with random decrements are given in [Reference Helland and Nilsen21, Section 2].
$(X_n)_{n \geq 0}$
from (1) via normalization. In Section 3 we will present some concrete examples, and we also want to mention that results on positive recurrence of more general exchange processes with random decrements are given in [Reference Helland and Nilsen21, Section 2].
Our first main result is an analogue to Theorem 1, which characterizes transience of the random exchange process
![]() $(X_n)_{n \geq 0}$
.
$(X_n)_{n \geq 0}$
.
Theorem 2.
For any law
![]() $\mu$
, the following statements are equivalent.
$\mu$
, the following statements are equivalent.
-
(a) There exists
 $n \in \mathbb{N}$
with
$n \in \mathbb{N}$
with
 $\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely.
$\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely.
-
(b) For all
 $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
 $\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely.
$\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely.
-
(c) The Markov chain
 $(X_n)_{n \geq 0}$
is transient.
$(X_n)_{n \geq 0}$
is transient.
-
(d)
 $\sum_{m \geq 0} \prod_{k=1}^m \sum_{l=0}^{k-1} \mu_l < \infty$
.
$\sum_{m \geq 0} \prod_{k=1}^m \sum_{l=0}^{k-1} \mu_l < \infty$
.
Moreover, if one of these conditions is satisfied, then
![]() $\mathbb{E} \big[\# V_\mu^c \big( \mathbb{N}_0^n\big)\big] < \infty$
for all
$\mathbb{E} \big[\# V_\mu^c \big( \mathbb{N}_0^n\big)\big] < \infty$
for all
![]() $n \in \mathbb{N}$
and there exists
$n \in \mathbb{N}$
and there exists
![]() $\alpha \in (0,\infty)$
with
$\alpha \in (0,\infty)$
with
![]() $\mathbb{E} \big[\!\exp \big( \alpha \# V_\mu^c \big( \mathbb{N}_0\big)\big)\big] < \infty$
.
$\mathbb{E} \big[\!\exp \big( \alpha \# V_\mu^c \big( \mathbb{N}_0\big)\big)\big] < \infty$
.
This theorem improves on previous works by revealing that, rather surprisingly, the value of
![]() $n \in \mathbb{N}$
does not influence whether all but finitely many points of the graph
$n \in \mathbb{N}$
does not influence whether all but finitely many points of the graph
![]() $\mathbb{N}_0^n$
are covered by a distribution
$\mathbb{N}_0^n$
are covered by a distribution
![]() $\mu$
. In the appendix of Lamperti’s paper [Reference Lamperti27], Kesten gives a proof of the fact that
$\mu$
. In the appendix of Lamperti’s paper [Reference Lamperti27], Kesten gives a proof of the fact that
![]() $\# V_\mu^c ( \mathbb{N}_0) < \infty$
almost surely if and only if condition (d) in Theorem 2 is satisfied. This result was later rediscovered by various authors, partly in a different and more general form; see [Reference Kellerer26, comments to Proposition 6.6], [Reference Junior, Machado and Zuluaga24, Theorem 2.1], [Reference Gallo, Garcia, Junior and Rodrguez15, Theorem 1], [Reference Bertacchi and Zucca6, Section 3], and [Reference Bezborodov and Krueger8, Section 3].
$\# V_\mu^c ( \mathbb{N}_0) < \infty$
almost surely if and only if condition (d) in Theorem 2 is satisfied. This result was later rediscovered by various authors, partly in a different and more general form; see [Reference Kellerer26, comments to Proposition 6.6], [Reference Junior, Machado and Zuluaga24, Theorem 2.1], [Reference Gallo, Garcia, Junior and Rodrguez15, Theorem 1], [Reference Bertacchi and Zucca6, Section 3], and [Reference Bezborodov and Krueger8, Section 3].
As observed by Zerner [Reference Zerner36, Proposition 1.1] and suggested by our notation, we can couple the set of covered points
![]() $V_\mu ( \mathbb{N}_0)$
and the random exchange process
$V_\mu ( \mathbb{N}_0)$
and the random exchange process
![]() $(X_n)_{n \geq 0}$
by using the same sequence of random variables
$(X_n)_{n \geq 0}$
by using the same sequence of random variables
![]() $(Y_n)_{n \geq 0}$
in both definitions. Then, by construction,
$(Y_n)_{n \geq 0}$
in both definitions. Then, by construction,
 \begin{align*}V_\mu ( \mathbb{N}_0)&= \{ n \in \mathbb{N}_0\mid \exists k \in \{0,\ldots,n\} \,:\, Y_k > n - k \}\\&= \Bigl\{ n \in \mathbb{N}_0 \bigm| \max_{0 \leq k \leq n} ( Y_k - (n-k) ) > 0 \Bigr\}\\&= \{ n \in \mathbb{N}_0\mid X_{n} > 0 \}.\end{align*}
\begin{align*}V_\mu ( \mathbb{N}_0)&= \{ n \in \mathbb{N}_0\mid \exists k \in \{0,\ldots,n\} \,:\, Y_k > n - k \}\\&= \Bigl\{ n \in \mathbb{N}_0 \bigm| \max_{0 \leq k \leq n} ( Y_k - (n-k) ) > 0 \Bigr\}\\&= \{ n \in \mathbb{N}_0\mid X_{n} > 0 \}.\end{align*}
Consequently, we know that the Markov chain
![]() $(X_n)_{n \geq 0}$
is transient if and only if
$(X_n)_{n \geq 0}$
is transient if and only if
![]() $\# V_\mu^c ( \mathbb{N}_0 ) < \infty$
almost surely.
$\# V_\mu^c ( \mathbb{N}_0 ) < \infty$
almost surely.
Let
![]() $n \geq 2$
and consider the infinite directed n-ary tree
$n \geq 2$
and consider the infinite directed n-ary tree
![]() $\mathcal{D}_n = (V_n, E_n)$
. Then, interestingly, we can associate a multitype branching process
$\mathcal{D}_n = (V_n, E_n)$
. Then, interestingly, we can associate a multitype branching process
![]() $(Z_m)_{m \geq 0}$
to our percolation model on
$(Z_m)_{m \geq 0}$
to our percolation model on
![]() $\mathcal{D}_n$
in the following way.
$\mathcal{D}_n$
in the following way.
Let
![]() $k \in \mathbb{N}_0$
and
$k \in \mathbb{N}_0$
and
![]() $y \in V_n$
with
$y \in V_n$
with
![]() $d(\emptyset,y)=k$
. Then we identify the vertex y with an individual of the kth generation of
$d(\emptyset,y)=k$
. Then we identify the vertex y with an individual of the kth generation of
![]() $(Z_m)_{m \geq 0}$
if and only if
$(Z_m)_{m \geq 0}$
if and only if
![]() $y \in V_\mu$
and y is contained in the same cluster as the root
$y \in V_\mu$
and y is contained in the same cluster as the root
![]() $\emptyset$
. In other words, we demand that all vertices forming the path from
$\emptyset$
. In other words, we demand that all vertices forming the path from
![]() $\emptyset$
to y in
$\emptyset$
to y in
![]() $\mathcal{D}_n$
are contained in
$\mathcal{D}_n$
are contained in
![]() $V_\mu ( \mathcal{D}_n)$
. If this condition is satisfied, we define the type of y by
$V_\mu ( \mathcal{D}_n)$
. If this condition is satisfied, we define the type of y by
By construction, if
![]() $Y_\emptyset \geq 1$
, the branching process
$Y_\emptyset \geq 1$
, the branching process
![]() $(Z_n)_{n \geq 0}$
starts with one individual of type
$(Z_n)_{n \geq 0}$
starts with one individual of type
![]() $Y_\emptyset$
. However, on the event
$Y_\emptyset$
. However, on the event
![]() $Y_\emptyset = 0$
, there are no individuals at all. For a vertex
$Y_\emptyset = 0$
, there are no individuals at all. For a vertex
![]() $y \in V_n$
to be identified with an individual in
$y \in V_n$
to be identified with an individual in
![]() $(Z_m)_{n \geq 0}$
, necessarily
$(Z_m)_{n \geq 0}$
, necessarily
![]() $y \in V_\mu$
, i.e. there exists
$y \in V_\mu$
, i.e. there exists
![]() $x \in V_n$
with
$x \in V_n$
with
![]() $Y_x > d(x,y)$
. Hence, as
$Y_x > d(x,y)$
. Hence, as
![]() $\mu_0 \in (0,1)$
, the type space of the branching process
$\mu_0 \in (0,1)$
, the type space of the branching process
![]() $(Z_m)_{n \geq 0}$
is
$(Z_m)_{n \geq 0}$
is
![]() $\mathcal{Z} = \mathcal{X} \setminus \{ 0 \}$
.
$\mathcal{Z} = \mathcal{X} \setminus \{ 0 \}$
.
We can describe the reproduction in this branching process as follows. Every individual has up to n children, and given the type of the parent, the types of the children are independent. Moreover, every individual of type
![]() $x \geq 2$
has exactly n children. For each of them, the probability of type
$x \geq 2$
has exactly n children. For each of them, the probability of type
![]() $y \in \mathcal{Z}$
is
$y \in \mathcal{Z}$
is
![]() $M_{x,y}\,:\!=\, P_{x,y}$
. On the other hand, an individual of type 1 has n potential children, which are again independent of each other. For all
$M_{x,y}\,:\!=\, P_{x,y}$
. On the other hand, an individual of type 1 has n potential children, which are again independent of each other. For all
![]() $z \in \mathcal{Z}$
, the probability that a given potential child is born and of type z is
$z \in \mathcal{Z}$
, the probability that a given potential child is born and of type z is
![]() $M_{1,z}\,:\!=\, P_{1,z} $
. However, with probability
$M_{1,z}\,:\!=\, P_{1,z} $
. However, with probability
![]() $\mu_0$
, a potential child is not born.
$\mu_0$
, a potential child is not born.
As the type space
![]() $\mathcal{Z}$
is infinite in general, we distinguish between the local and global extinction of
$\mathcal{Z}$
is infinite in general, we distinguish between the local and global extinction of
![]() $(Z_m)_{m \geq 0}$
. This process dies out globally if, at some moment, the total number of individuals vanishes. It dies out locally if, for all
$(Z_m)_{m \geq 0}$
. This process dies out globally if, at some moment, the total number of individuals vanishes. It dies out locally if, for all
![]() $z \in \mathcal{Z}$
, only finitely many individuals of type z are born. While global extinction always implies local extinction, the reverse is not true in general for branching processes with infinitely many types.
$z \in \mathcal{Z}$
, only finitely many individuals of type z are born. While global extinction always implies local extinction, the reverse is not true in general for branching processes with infinitely many types.
Theorem 3.
Let
![]() $n \geq 2$
. Then, for any distribution
$n \geq 2$
. Then, for any distribution
![]() $\mu$
,
$\mu$
,
![]() $\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely. Moreover, the following statements are equivalent.
$\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely. Moreover, the following statements are equivalent.
-
(A) Almost surely,
 $V_\mu ( \mathcal{D}_n)$
contains a path of infinite length.
$V_\mu ( \mathcal{D}_n)$
contains a path of infinite length.
-
(B) With positive probability,
 $(Z_m)_{m \geq 0}$
will not die out globally.
$(Z_m)_{m \geq 0}$
will not die out globally.
-
(C) With positive probability,
 $(Z_m)_{m \geq 0}$
will not die out locally.
$(Z_m)_{m \geq 0}$
will not die out locally.
-
(D)
 $\rho (M) > n^{-1}$
, where
$\rho (M) > n^{-1}$
, where
 $M\,:\!=\, (M_{x,y})_{x,y \in \mathcal{Z}}$
.
$M\,:\!=\, (M_{x,y})_{x,y \in \mathcal{Z}}$
.
If one of these statements holds, then almost surely
![]() $V_\mu ( \mathcal{D}_n)$
contains infinitely many distinct infinite clusters. Otherwise, almost surely there are no infinite clusters in
$V_\mu ( \mathcal{D}_n)$
contains infinitely many distinct infinite clusters. Otherwise, almost surely there are no infinite clusters in
![]() $V_\mu ( \mathcal{D}_n)$
.
$V_\mu ( \mathcal{D}_n)$
.
Note that, up to multiplication with
![]() $n \geq 2$
, M is the mean matrix of the branching process
$n \geq 2$
, M is the mean matrix of the branching process
![]() $(Z_m)_{m \geq 0}$
. To some degree, this explains why condition (D) is related to (B) and (C). Also, observe that M arises from the transition matrix P of the random exchange process
$(Z_m)_{m \geq 0}$
. To some degree, this explains why condition (D) is related to (B) and (C). Also, observe that M arises from the transition matrix P of the random exchange process
![]() $(X_n)_{n \geq 0}$
simply by deleting both the first row and first column.
$(X_n)_{n \geq 0}$
simply by deleting both the first row and first column.
For an introduction to infinite-type branching processes, we recommend Braunsteins’ exposition [Reference Braunsteins9, Chapter 2] and the references mentioned therein. This presentation also explains the rather well-understood results on the extinction of finite-type branching processes.
We also want to note that the branching processes
![]() $(Z_n)_{n \geq 0}$
, which we consider in the present article, have a mean matrix of upper Hessenberg form. Recently, Braunsteins and Haupthenne [Reference Braunsteins and Haupthenne10] studied the extinction of branching processes with a lower Hessenberg mean matrix.
$(Z_n)_{n \geq 0}$
, which we consider in the present article, have a mean matrix of upper Hessenberg form. Recently, Braunsteins and Haupthenne [Reference Braunsteins and Haupthenne10] studied the extinction of branching processes with a lower Hessenberg mean matrix.
2. Proof of Theorems 2 and 3
Proof of Theorem 2. (b)
![]() $\Longrightarrow$
(c)
$\Longrightarrow$
(c)
![]() $\Longrightarrow$
(a) From our coupling between
$\Longrightarrow$
(a) From our coupling between
![]() $V_\mu ( \mathbb{N}_0)$
and
$V_\mu ( \mathbb{N}_0)$
and
![]() $(X_n)_{n \geq 0}$
, we know that
$(X_n)_{n \geq 0}$
, we know that
![]() $(X_n)_{n \geq 0}$
is transient if and only if
$(X_n)_{n \geq 0}$
is transient if and only if
![]() $V_\mu^c ( \mathbb{N}_0) < \infty$
almost surely. In particular, the implications (b)
$V_\mu^c ( \mathbb{N}_0) < \infty$
almost surely. In particular, the implications (b)
![]() $\Longrightarrow$
(c) and (c)
$\Longrightarrow$
(c) and (c)
![]() $\Longrightarrow$
(a) follow.
$\Longrightarrow$
(a) follow.
(d)
![]() $\Longrightarrow$
(a) By Kolmogorov’s 0–1 law, for any probability distribution
$\Longrightarrow$
(a) By Kolmogorov’s 0–1 law, for any probability distribution
![]() $\mu$
, either
$\mu$
, either
![]() $\# V_\mu^c ( \mathbb{N}_0) < \infty$
almost surely or
$\# V_\mu^c ( \mathbb{N}_0) < \infty$
almost surely or
![]() $\#V_\mu^c ( \mathbb{N}_0) = \infty$
almost surely. By observing
$\#V_\mu^c ( \mathbb{N}_0) = \infty$
almost surely. By observing
 \begin{equation}\mathbb{E} \big[\# V_\mu^c \big( \mathbb{N}_0\big) \big] = \sum_{m \geq 0} q_m = \sum_{m \geq 0} \prod_{k=1}^m \sum_{l=0}^{k-1} \mu_l,\end{equation}
\begin{equation}\mathbb{E} \big[\# V_\mu^c \big( \mathbb{N}_0\big) \big] = \sum_{m \geq 0} q_m = \sum_{m \geq 0} \prod_{k=1}^m \sum_{l=0}^{k-1} \mu_l,\end{equation}
where
![]() $q_m \,:\!=\, P \big[ m \in V_\mu^c \big( \mathbb{N}_0\big)\big]$
for all
$q_m \,:\!=\, P \big[ m \in V_\mu^c \big( \mathbb{N}_0\big)\big]$
for all
![]() $m \geq 0$
, the implication follows.
$m \geq 0$
, the implication follows.
Finally, let us assume that condition (a) holds for a distribution
![]() $\mu$
. We will show (a)
$\mu$
. We will show (a)
![]() $\Longrightarrow$
(d) and (a)
$\Longrightarrow$
(d) and (a)
![]() $\Longrightarrow$
(b).
$\Longrightarrow$
(b).
In the first step, we verify that we can restrict ourselves to the case
![]() $n=1$
. For this, suppose
$n=1$
. For this, suppose
![]() $\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely for some
$\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely for some
![]() $n \geq 2$
. Then, consider the subgraph
$n \geq 2$
. Then, consider the subgraph
![]() $\mathcal{G}^{\prime}=(V^{\prime},E^{\prime})$
of
$\mathcal{G}^{\prime}=(V^{\prime},E^{\prime})$
of
![]() $\mathbb{N}_0^n$
, which is induced by the vertex set V
′ of all
$\mathbb{N}_0^n$
, which is induced by the vertex set V
′ of all
![]() $(x_1,\ldots,x_n) \in \mathbb{N}_0^n$
with
$(x_1,\ldots,x_n) \in \mathbb{N}_0^n$
with
![]() $x_j = 0$
for all
$x_j = 0$
for all
![]() $j=2,\ldots,n$
. By construction,
$j=2,\ldots,n$
. By construction,
![]() $\mathcal{G}^{\prime}$
is isomorphic to
$\mathcal{G}^{\prime}$
is isomorphic to
![]() $\mathbb{N}_0$
, and we know that
$\mathbb{N}_0$
, and we know that
![]() $V_\mu^c ( \mathcal{G}^{\prime}) = V_\mu^c \big( \mathbb{N}_0^n\big) \cap V^{\prime}$
is finite almost surely. Consequently,
$V_\mu^c ( \mathcal{G}^{\prime}) = V_\mu^c \big( \mathbb{N}_0^n\big) \cap V^{\prime}$
is finite almost surely. Consequently,
![]() $\# V_\mu^c ( \mathbb{N}_0 ) < \infty$
almost surely.
$\# V_\mu^c ( \mathbb{N}_0 ) < \infty$
almost surely.
In the second step, we prove all remaining claims. As
![]() $0 < \mu_0 < 1$
,
$0 < \mu_0 < 1$
,
Therefore, by the strong Markov property, we know that
![]() $\# V_\mu^c ( \mathbb{N}_0)$
is geometrically distributed with parameter p. In particular, this random variable has a finite exponential moment, and moreover, we can deduce (d) via (2).
$\# V_\mu^c ( \mathbb{N}_0)$
is geometrically distributed with parameter p. In particular, this random variable has a finite exponential moment, and moreover, we can deduce (d) via (2).
Let
![]() $n \in \mathbb{N}$
and
$n \in \mathbb{N}$
and
![]() $x=(x_1,\ldots,x_n) \in \mathbb{N}_0^n$
. For all
$x=(x_1,\ldots,x_n) \in \mathbb{N}_0^n$
. For all
![]() $j=1,\ldots,n$
, let
$j=1,\ldots,n$
, let
![]() $\pi_j$
denote the unique path from
$\pi_j$
denote the unique path from
![]() $(x_1,\ldots,x_{j-1},0,x_{j+1},\ldots,x_n)$
to x. Then, for all
$(x_1,\ldots,x_{j-1},0,x_{j+1},\ldots,x_n)$
to x. Then, for all
![]() $j=1,\ldots,n$
, the path
$j=1,\ldots,n$
, the path
![]() $\pi_j$
consists of
$\pi_j$
consists of
![]() $x_j$
edges in direction
$x_j$
edges in direction
![]() $e_j$
, and, for all
$e_j$
, and, for all
![]() $i \neq j$
, the paths
$i \neq j$
, the paths
![]() $\pi_i$
and
$\pi_i$
and
![]() $\pi_j$
only share one vertex, which is their endpoint
$\pi_j$
only share one vertex, which is their endpoint
![]() $x =(x_1,\ldots,x_n)$
. So, for the event
$x =(x_1,\ldots,x_n)$
. So, for the event
![]() $\big\{ x \in V_\mu^c \big(\mathbb{N}_0^n\big) \big\}$
to occur, it is necessary that for each
$\big\{ x \in V_\mu^c \big(\mathbb{N}_0^n\big) \big\}$
to occur, it is necessary that for each
![]() $j=1,\ldots,n$
there exists no vertex y contained in the path
$j=1,\ldots,n$
there exists no vertex y contained in the path
![]() $\pi_j$
such that
$\pi_j$
such that
![]() $Z_y > d(y,x)$
. This defines n independent events, whose probabilities can be described with the sequence
$Z_y > d(y,x)$
. This defines n independent events, whose probabilities can be described with the sequence
![]() $(q_m)_{m \geq 0}$
defined above. All in all,
$(q_m)_{m \geq 0}$
defined above. All in all,
 \begin{align*} \mathbb{E} \bigl[ \# V_\mu^c \big( \mathbb{N}_0^n\big) \bigr]&= \sum_{x \in \mathbb{N}_0^n} \mathbb{P} \bigl[ x \in V_\mu^c \big( \mathbb{N}_0^n\big) \bigr] \\ &\leq \sum_{(x_1,\ldots,x_n) \in \mathbb{N}_0^n}\ \prod_{j=1}^n\ q_{x_j}\\&= \sum_{x_1 \geq 0} q_{x_1} \sum_{x_2 \geq 0} q_{x_2} \cdots \sum_{x_{n-1} \geq 0} q_{x_{n-1}} \sum_{x_n \geq 0} q_{x_n}\\ &= \mathbb{E} \bigl[\# V_\mu^c \big( \mathbb{N}_0\big) \bigr]^n \\ &< \infty .\end{align*}
\begin{align*} \mathbb{E} \bigl[ \# V_\mu^c \big( \mathbb{N}_0^n\big) \bigr]&= \sum_{x \in \mathbb{N}_0^n} \mathbb{P} \bigl[ x \in V_\mu^c \big( \mathbb{N}_0^n\big) \bigr] \\ &\leq \sum_{(x_1,\ldots,x_n) \in \mathbb{N}_0^n}\ \prod_{j=1}^n\ q_{x_j}\\&= \sum_{x_1 \geq 0} q_{x_1} \sum_{x_2 \geq 0} q_{x_2} \cdots \sum_{x_{n-1} \geq 0} q_{x_{n-1}} \sum_{x_n \geq 0} q_{x_n}\\ &= \mathbb{E} \bigl[\# V_\mu^c \big( \mathbb{N}_0\big) \bigr]^n \\ &< \infty .\end{align*}
In particular, for all
![]() $n \geq 2$
,
$n \geq 2$
,
![]() $\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely, and condition (b) holds. Since we have already verified (b)
$\# V_\mu^c \big( \mathbb{N}_0^n\big) < \infty$
almost surely, and condition (b) holds. Since we have already verified (b)
![]() $\Longrightarrow$
(c), this finishes the proof.
$\Longrightarrow$
(c), this finishes the proof.
Proof of Theorem 3. First we verify that for all
![]() $n \geq 2$
and any law
$n \geq 2$
and any law
![]() $\mu$
,
$\mu$
,
![]() $\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely. For this, for all
$\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely. For this, for all
![]() $m \in \mathbb{N}$
, we set
$m \in \mathbb{N}$
, we set
As
![]() $0 < \mu_0 < 1$
, we know that
$0 < \mu_0 < 1$
, we know that
![]() $r_m \in (0,1)$
for all
$r_m \in (0,1)$
for all
![]() $m \in \mathbb{N}$
. Moreover, for all
$m \in \mathbb{N}$
. Moreover, for all
![]() $j=1,\ldots,n$
, we let
$j=1,\ldots,n$
, we let
![]() $\mathcal{G}_j$
denote the induced subgraph obtained from
$\mathcal{G}_j$
denote the induced subgraph obtained from
![]() $\mathcal{D}_n$
by restricting to all vertices, which can be reached from
$\mathcal{D}_n$
by restricting to all vertices, which can be reached from
![]() $j \in V_n$
.
$j \in V_n$
.
Let
![]() $m \geq 2$
. Then we know that there exists a
$m \geq 2$
. Then we know that there exists a
![]() $y \in V_\mu^c ( \mathcal{D}_n)$
with
$y \in V_\mu^c ( \mathcal{D}_n)$
with
![]() $d(\emptyset,y)=m$
if and only if
$d(\emptyset,y)=m$
if and only if
![]() $Y_\emptyset \leq m$
and, for some
$Y_\emptyset \leq m$
and, for some
![]() $j=1,\ldots,n$
, there exists a vertex z in the graph
$j=1,\ldots,n$
, there exists a vertex z in the graph
![]() $\mathcal{G}_j$
with
$\mathcal{G}_j$
with
![]() $d(j,z)=m-1$
, which is not covered by any other vertex of
$d(j,z)=m-1$
, which is not covered by any other vertex of
![]() $\mathcal{G}_j$
. Note that the latter event is independent of
$\mathcal{G}_j$
. Note that the latter event is independent of
![]() $Y_\emptyset$
and that the graphs
$Y_\emptyset$
and that the graphs
![]() $\mathcal{G}_1,\ldots,\mathcal{G}_n$
are isomorphic to
$\mathcal{G}_1,\ldots,\mathcal{G}_n$
are isomorphic to
![]() $\mathcal{D}_n$
. Consequently, for all
$\mathcal{D}_n$
. Consequently, for all
![]() $m \geq 1$
, we obtain the recurrence relation
$m \geq 1$
, we obtain the recurrence relation
 \begin{equation}r_{m+1} = ( 1 - (1 - r_m)^n )\ F(m+1), \quad \text{where} \ F(k) \,:\!=\, \sum_{l=0}^k \mu_l.\end{equation}
\begin{equation}r_{m+1} = ( 1 - (1 - r_m)^n )\ F(m+1), \quad \text{where} \ F(k) \,:\!=\, \sum_{l=0}^k \mu_l.\end{equation}
Let
![]() $N \in \mathbb{N}$
with
$N \in \mathbb{N}$
with
![]() $F(N) > 1/2$
. Then, by (3), for all
$F(N) > 1/2$
. Then, by (3), for all
![]() $m \geq N$
,
$m \geq N$
,
The map
![]() $f_N\,:\, [0,1] \rightarrow [0,1]$
,
$f_N\,:\, [0,1] \rightarrow [0,1]$
,
![]() $x \mapsto x (2-x) F(N)$
, is monotone increasing. Hence, due to the estimate (4), iteration of the function
$x \mapsto x (2-x) F(N)$
, is monotone increasing. Hence, due to the estimate (4), iteration of the function
![]() $f_N$
yields
$f_N$
yields
The map
![]() $f_N$
has the two fixed points 0 and
$f_N$
has the two fixed points 0 and
![]() $x_N\,:\!=\, 2- F(N)^{-1} \in (0,1]$
. Hence, by monotonicity, if
$x_N\,:\!=\, 2- F(N)^{-1} \in (0,1]$
. Hence, by monotonicity, if
![]() $r_N \geq x_N$
, then also
$r_N \geq x_N$
, then also
![]() $r_m \geq x_N$
for all
$r_m \geq x_N$
for all
![]() $m \geq N$
. On the other hand, if
$m \geq N$
. On the other hand, if
![]() $r_N < x_N$
, then, since
$r_N < x_N$
, then, since
![]() $f_N$
is concave and
$f_N$
is concave and
![]() $f^{\prime}_N (0) > 1$
, we have
$f^{\prime}_N (0) > 1$
, we have
![]() $f_N^k ( r_N) \rightarrow x_N$
for
$f_N^k ( r_N) \rightarrow x_N$
for
![]() $k \rightarrow \infty$
. In both cases, we can deduce
$k \rightarrow \infty$
. In both cases, we can deduce
As
![]() $N \in \mathbb{N}$
can be chosen arbitrarily large in this argument, it follows that
$N \in \mathbb{N}$
can be chosen arbitrarily large in this argument, it follows that
![]() $r_m \rightarrow 1$
for
$r_m \rightarrow 1$
for
![]() $m \rightarrow \infty$
. In particular,
$m \rightarrow \infty$
. In particular,
![]() $V_\mu^c ( \mathcal{D}_n)$
is almost surely non-empty.
$V_\mu^c ( \mathcal{D}_n)$
is almost surely non-empty.
By Kolmogorov’s 0–1 law, we know that either
![]() $\# V_\mu^c ( \mathcal{D}_n)$
is finite almost surely, or this random variable is infinite almost surely. In the first case, due to
$\# V_\mu^c ( \mathcal{D}_n)$
is finite almost surely, or this random variable is infinite almost surely. In the first case, due to
![]() $\mu_0 \in (0,1)$
, it would follow that
$\mu_0 \in (0,1)$
, it would follow that
![]() $V_\mu^c ( \mathcal{D}_n)$
is empty with probability greater than zero. As this is not possible, we can conclude
$V_\mu^c ( \mathcal{D}_n)$
is empty with probability greater than zero. As this is not possible, we can conclude
![]() $\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely.
$\# V_\mu^c ( \mathcal{D}_n) = \infty$
almost surely.
In the second step of this proof, we now verify that indeed the statements (A), (B), (C), and (D) are equivalent to each other.
(C)
![]() $\Longrightarrow$
(B) This implication is clear.
$\Longrightarrow$
(B) This implication is clear.
(A)
![]() $\Longleftrightarrow$
(B) If (A) holds, then, with positive probability,
$\Longleftrightarrow$
(B) If (A) holds, then, with positive probability,
![]() $V_\mu( \mathcal{D}_n)$
contains an infinite path starting from the root
$V_\mu( \mathcal{D}_n)$
contains an infinite path starting from the root
![]() $\emptyset$
. On this event,
$\emptyset$
. On this event,
![]() $(Z_n)_{n \geq 0}$
does not die out globally, i.e. condition (B) holds. Conversely, if (B) holds, then, with positive probability,
$(Z_n)_{n \geq 0}$
does not die out globally, i.e. condition (B) holds. Conversely, if (B) holds, then, with positive probability,
![]() $V_\mu ( \mathcal{D}_n)$
contains an infinite path. By Kolmogorov’s 0-1 law, (A) follows.
$V_\mu ( \mathcal{D}_n)$
contains an infinite path. By Kolmogorov’s 0-1 law, (A) follows.
(C)
![]() $\Longleftrightarrow$
(D) Since the mean matrix M of the branching process
$\Longleftrightarrow$
(D) Since the mean matrix M of the branching process
![]() $(Z_n)_{n \geq 0}$
is irreducible, this equivalence follows from the theory of multitype branching processes; see [Reference Braunsteins9, Theorem 9], [Reference Gantert and Müller16], and [Reference Bertacchi and Zucca5].
$(Z_n)_{n \geq 0}$
is irreducible, this equivalence follows from the theory of multitype branching processes; see [Reference Braunsteins9, Theorem 9], [Reference Gantert and Müller16], and [Reference Bertacchi and Zucca5].
(B)
![]() $\Longrightarrow$
(C) Suppose, for some distribution
$\Longrightarrow$
(C) Suppose, for some distribution
![]() $\mu$
, that
$\mu$
, that
![]() $(Z_n)_{n \geq 0}$
dies out locally almost surely but survives forever with positive probability. Then, as
$(Z_n)_{n \geq 0}$
dies out locally almost surely but survives forever with positive probability. Then, as
![]() $(Z_n)_{n \geq 0}$
starts with a single individual of random type
$(Z_n)_{n \geq 0}$
starts with a single individual of random type
![]() $Y_\emptyset$
, with some positive probability,
$Y_\emptyset$
, with some positive probability,
![]() $(Z_n)_{n \geq 0}$
survives forever, and no individuals of type 1 are born. On this event, we would know that
$(Z_n)_{n \geq 0}$
survives forever, and no individuals of type 1 are born. On this event, we would know that
![]() $\# V_\mu^c ( \mathcal{D}_n) < \infty$
, and this is a contradiction to our first claim. The implication follows.
$\# V_\mu^c ( \mathcal{D}_n) < \infty$
, and this is a contradiction to our first claim. The implication follows.
Finally, let us verify the two claims regarding infinite clusters of
![]() $V_\mu ( \mathcal{D}_n)$
. Note that
$V_\mu ( \mathcal{D}_n)$
. Note that
![]() $V_\mu ( \mathcal{D}_n)$
contains an infinite cluster if and only if it contains an infinite path, and due to Kolmogorov’s 0–1 law the probability for this is either 0 or 1. So, we only need to prove that if
$V_\mu ( \mathcal{D}_n)$
contains an infinite cluster if and only if it contains an infinite path, and due to Kolmogorov’s 0–1 law the probability for this is either 0 or 1. So, we only need to prove that if
![]() $V_\mu ( \mathcal{D}_n)$
contains an infinite path almost surely, then there exist infinitely many such paths so that every path of this collection is contained in a separate cluster of
$V_\mu ( \mathcal{D}_n)$
contains an infinite path almost surely, then there exist infinitely many such paths so that every path of this collection is contained in a separate cluster of
![]() $V_\mu ( \mathcal{D}_n)$
.
$V_\mu ( \mathcal{D}_n)$
.
First, let us extend some of our notation. For a vertex y in
![]() $\mathcal{D}_n$
, let
$\mathcal{D}_n$
, let
![]() $\mathcal{G}_{y}$
again denote the subgraph of
$\mathcal{G}_{y}$
again denote the subgraph of
![]() $\mathcal{D}_n$
that arises by restricting to the vertex y and all vertices z of
$\mathcal{D}_n$
that arises by restricting to the vertex y and all vertices z of
![]() $\mathcal{D}_n$
with
$\mathcal{D}_n$
with
![]() $d(y,z) < \infty$
. Again, this graph is isomorphic to
$d(y,z) < \infty$
. Again, this graph is isomorphic to
![]() $\mathcal{D}_n$
.
$\mathcal{D}_n$
.
Choose a sequence of vertices
![]() $(y_k)_{k \geq 1}$
in
$(y_k)_{k \geq 1}$
in
![]() $\mathcal{D}_n$
so that the vertex sets of the graphs
$\mathcal{D}_n$
so that the vertex sets of the graphs
![]() $\mathcal{G}_{y_k}$
,
$\mathcal{G}_{y_k}$
,
![]() $k \geq 1$
, are pairwise disjoint.
$k \geq 1$
, are pairwise disjoint.
Now, we first verify that for any choice of
![]() $\mu$
and for all
$\mu$
and for all
![]() $k \geq 1$
, almost surely infinitely many vertices of
$k \geq 1$
, almost surely infinitely many vertices of
![]() $\mathcal{G}_{y_k}$
are not covered. For this, note that as
$\mathcal{G}_{y_k}$
are not covered. For this, note that as
![]() $\mu_0 > 0$
, with positive probability all vertices x in
$\mu_0 > 0$
, with positive probability all vertices x in
![]() $\mathcal{D}_n$
with
$\mathcal{D}_n$
with
![]() $d(x,y_k) < \infty$
and
$d(x,y_k) < \infty$
and
![]() $x \neq y_k$
satisfy
$x \neq y_k$
satisfy
![]() $x \in V_\mu^c ( \mathcal{D}_n)$
. On this event, as
$x \in V_\mu^c ( \mathcal{D}_n)$
. On this event, as
![]() $\mathcal{D}_{n}$
and
$\mathcal{D}_{n}$
and
![]() $\mathcal{G}_{y_k}$
are isomorphic, we know that almost surely infinitely many vertices of
$\mathcal{G}_{y_k}$
are isomorphic, we know that almost surely infinitely many vertices of
![]() $\mathcal{G}_{y_k}$
are contained in
$\mathcal{G}_{y_k}$
are contained in
![]() $V_\mu^c ( \mathcal{D}_n)$
. So, by Kolmogorov’s 0–1 law, indeed for all
$V_\mu^c ( \mathcal{D}_n)$
. So, by Kolmogorov’s 0–1 law, indeed for all
![]() $\mu$
and
$\mu$
and
![]() $k \geq 1$
, infinitely many vertices of
$k \geq 1$
, infinitely many vertices of
![]() $\mathcal{G}_{y_k}$
are not covered by
$\mathcal{G}_{y_k}$
are not covered by
![]() $\mu$
.
$\mu$
.
As a consequence, for all
![]() $k \geq 1$
, we can choose a random vertex
$k \geq 1$
, we can choose a random vertex
![]() $w_k$
in
$w_k$
in
![]() $\mathcal{G}_{y_k}$
that satisfies
$\mathcal{G}_{y_k}$
that satisfies
![]() $w_k \in V_\mu^c ( \mathcal{D}_n)$
almost surely (for example, choose the smallest element of
$w_k \in V_\mu^c ( \mathcal{D}_n)$
almost surely (for example, choose the smallest element of
![]() $V_\mu^c ( \mathcal{D}_n)$
in
$V_\mu^c ( \mathcal{D}_n)$
in
![]() $\mathcal{G}_{y_k}$
with respect to the lexicographical order). Consider, for all
$\mathcal{G}_{y_k}$
with respect to the lexicographical order). Consider, for all
![]() $k \geq 1$
, the random subgraph
$k \geq 1$
, the random subgraph
![]() $\mathcal{G}_{w_k}$
of
$\mathcal{G}_{w_k}$
of
![]() $\mathcal{G}_{y_k}$
. As these graphs are almost surely isomorphic to
$\mathcal{G}_{y_k}$
. As these graphs are almost surely isomorphic to
![]() $\mathcal{D}_n$
, almost surely each of them contains an infinite path using only vertices from
$\mathcal{D}_n$
, almost surely each of them contains an infinite path using only vertices from
![]() $V_\mu ( \mathcal{D}_n)$
. Moreover, as the graphs
$V_\mu ( \mathcal{D}_n)$
. Moreover, as the graphs
![]() $\mathcal{G}_{y_k}$
,
$\mathcal{G}_{y_k}$
,
![]() $k \geq 1$
, are disjoint, so are the random graphs
$k \geq 1$
, are disjoint, so are the random graphs
![]() $\mathcal{G}_{w_k}$
,
$\mathcal{G}_{w_k}$
,
![]() $k \geq 1$
, and these infinite paths. Finally, as
$k \geq 1$
, and these infinite paths. Finally, as
![]() $w_k \in V_\mu^c ( \mathcal{D}_n)$
almost surely, we also know that in this collection of infinite paths in
$w_k \in V_\mu^c ( \mathcal{D}_n)$
almost surely, we also know that in this collection of infinite paths in
![]() $V_\mu ( \mathcal{D}_n)$
, every path is contained in a separate cluster of
$V_\mu ( \mathcal{D}_n)$
, every path is contained in a separate cluster of
![]() $V_\mu ( \mathcal{D}_n)$
.
$V_\mu ( \mathcal{D}_n)$
.
3. Examples
Example 1. Let
![]() $m \in \mathbb{N}$
,
$m \in \mathbb{N}$
,
![]() $m \geq 2$
, and
$m \geq 2$
, and
![]() $\mu$
be the uniform distribution on
$\mu$
be the uniform distribution on
![]() $\{ 0,1,\ldots,m-1\}$
. Then, by (1), the stationary solution
$\{ 0,1,\ldots,m-1\}$
. Then, by (1), the stationary solution
![]() $\tau$
of
$\tau$
of
![]() $(X_n)_{n \geq 0}$
is
$(X_n)_{n \geq 0}$
is
This law
![]() $\tau$
is a terminating member of the Kemp family of generalized hypergeometric probability distributions; see [Reference Johnson, Kemp and Kotz22, Section 2.4.1]. However, it also naturally arises from Naor’s urn model [Reference Naor31, Appendix]; see also [Reference Johnson, Kemp and Kotz22, Section 11.2.12]. Assume that there are m balls in an urn, of which one is red and the rest are white. In each step, pick one ball, and if it is white, replace it with a red ball. Continue until the first time T at which a red ball gets chosen. Then the distribution of T is
$\tau$
is a terminating member of the Kemp family of generalized hypergeometric probability distributions; see [Reference Johnson, Kemp and Kotz22, Section 2.4.1]. However, it also naturally arises from Naor’s urn model [Reference Naor31, Appendix]; see also [Reference Johnson, Kemp and Kotz22, Section 11.2.12]. Assume that there are m balls in an urn, of which one is red and the rest are white. In each step, pick one ball, and if it is white, replace it with a red ball. Continue until the first time T at which a red ball gets chosen. Then the distribution of T is
and
![]() $m-T$
, i.e. the number of tries not needed, has distribution
$m-T$
, i.e. the number of tries not needed, has distribution
![]() $\tau$
.
$\tau$
.
Example 2. Let
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $\mu$
be the geometric distribution with parameter
$\mu$
be the geometric distribution with parameter
![]() $1-p$
. Then, by (2), the stationary solution
$1-p$
. Then, by (2), the stationary solution
![]() $\tau$
of
$\tau$
of
![]() $(X_n)_{n \geq 0}$
is
$(X_n)_{n \geq 0}$
is
 \[\tau_n = \tau_0\ p^n \Biggl( \prod_{k=1}^{n} ( 1 - p^{k} ) \Biggr)^{-1} = \tau_0 \ \dfrac{p^n}{(p;\,p)_n}, \quad n \in \mathbb{N}_0,\]
\[\tau_n = \tau_0\ p^n \Biggl( \prod_{k=1}^{n} ( 1 - p^{k} ) \Biggr)^{-1} = \tau_0 \ \dfrac{p^n}{(p;\,p)_n}, \quad n \in \mathbb{N}_0,\]
where
![]() $(a;\,q)_n$
is the q-Pochhammer symbol. By normalization,
$(a;\,q)_n$
is the q-Pochhammer symbol. By normalization,
 \[\tau_0 = \Biggl( \sum_{n \geq 0} \dfrac{p^n}{(p;\,p)_n} \Biggr)^{-1} = \dfrac{1}{(p;\,p)_{\infty}} = \phi(p)^{-1},\]
\[\tau_0 = \Biggl( \sum_{n \geq 0} \dfrac{p^n}{(p;\,p)_n} \Biggr)^{-1} = \dfrac{1}{(p;\,p)_{\infty}} = \phi(p)^{-1},\]
where we have applied the q-binomial theorem (see [Reference Olver, Lozier, Boisvert and Clark32, Section 17.2(iii)]), and
![]() $\phi$
denotes Euler’s function. Benkherouf and Bather [Reference Benkherouf and Bather4, Section 4] discussed this distribution
$\phi$
denotes Euler’s function. Benkherouf and Bather [Reference Benkherouf and Bather4, Section 4] discussed this distribution
![]() $\tau$
in a more general form, and referred to it as an Euler distribution. For more information, see also [Reference Johnson, Kemp and Kotz22, Section 10.8.2].
$\tau$
in a more general form, and referred to it as an Euler distribution. For more information, see also [Reference Johnson, Kemp and Kotz22, Section 10.8.2].
Example 3. Assume that there exists
![]() $c \in (0,\infty)$
and
$c \in (0,\infty)$
and
![]() $n_0 \in \mathbb{N}$
with
$n_0 \in \mathbb{N}$
with
Then, as the expectation of
![]() $\mu$
is infinite, we know that statements (i)–(iv) from Theorem 1 hold. Moreover,
$\mu$
is infinite, we know that statements (i)–(iv) from Theorem 1 hold. Moreover,
 \[\Biggl( \prod_{k=1}^{n+1} \sum_{l=0}^{k-1} \mu_l \Biggr) \Bigg/ \Biggl( \prod_{k=1}^{n} \sum_{l=0}^{k-1} \mu_l \Biggr) = \sum_{l=0}^{n+1} \mu_l = 1 - \dfrac{c}{n+1} \quad \text{for all $ n \geq n_0$,} \]
\[\Biggl( \prod_{k=1}^{n+1} \sum_{l=0}^{k-1} \mu_l \Biggr) \Bigg/ \Biggl( \prod_{k=1}^{n} \sum_{l=0}^{k-1} \mu_l \Biggr) = \sum_{l=0}^{n+1} \mu_l = 1 - \dfrac{c}{n+1} \quad \text{for all $ n \geq n_0$,} \]
and consequently, by the Gaussian ratio test, we know that condition (d) in Theorem 2 is satisfied if and only if
![]() $c>1$
. According to [Reference Helland and Nilsen21, Theorem 3.2], for any value of
$c>1$
. According to [Reference Helland and Nilsen21, Theorem 3.2], for any value of
![]() $c \in (0,\infty)$
,
$c \in (0,\infty)$
,
This limit is an inverse Beta distribution with
![]() $\alpha=c$
and
$\alpha=c$
and
![]() $\beta=1$
.
$\beta=1$
.
Example 4. Assume that
![]() $\mu = (\mu_n)_{n \geq 0}$
has finite support. Then
$\mu = (\mu_n)_{n \geq 0}$
has finite support. Then
![]() $(X_n)_{n \geq 0}$
has a stationary solution and
$(X_n)_{n \geq 0}$
has a stationary solution and
![]() $\rho(P)=1$
. Moreover,
$\rho(P)=1$
. Moreover,
![]() $\rho(M)$
is the spectral radius and Perron–Frobenius eigenvalue of M. As in the proof of Theorem 3, we define, for the case
$\rho(M)$
is the spectral radius and Perron–Frobenius eigenvalue of M. As in the proof of Theorem 3, we define, for the case
![]() $n=2$
,
$n=2$
,
Then, observe that for all
![]() $m \geq n_0 \,:\!=\, \sup \{ n \in \mathbb{N}\mid \mu_n \neq 0 \}$
, the recurrence relation (3) simplifies to
$m \geq n_0 \,:\!=\, \sup \{ n \in \mathbb{N}\mid \mu_n \neq 0 \}$
, the recurrence relation (3) simplifies to
This recursion is a modified version of the logistic equation. It follows that
where
![]() $c \in (0,\infty)$
is a fixed parameter.
$c \in (0,\infty)$
is a fixed parameter.
Example 5. Let
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $p \in (0,1)$
,
$p \in (0,1)$
,
![]() $\mu_n \,:\!=\, p$
, and
$\mu_n \,:\!=\, p$
, and
![]() $\mu_0\,:\!=\, 1-p$
. Then the matrix
$\mu_0\,:\!=\, 1-p$
. Then the matrix
![]() $M=M_{n,p}$
has dimension n and is of the form
$M=M_{n,p}$
has dimension n and is of the form
 \[M_{n,p} = \begin{pmatrix}0& \quad 0& \quad \cdots& \quad \cdots& \quad 0& \quad p\\[3pt]1-p& \quad 0& \quad \cdots& \quad \cdots& \quad 0& \quad p\\[3pt]0& \quad 1-p& \quad 0& \quad \cdots& \quad 0& \quad p\\[3pt]\vdots& \quad & \quad \ddots& \quad & \quad & \quad \vdots\\[3pt]\vdots& \quad & \quad & \quad \ddots& \quad & \quad \vdots\\[3pt]0& \quad \cdots& \quad \cdots& \quad 0& \quad 1-p& \quad p\end{pmatrix}\!.\]
\[M_{n,p} = \begin{pmatrix}0& \quad 0& \quad \cdots& \quad \cdots& \quad 0& \quad p\\[3pt]1-p& \quad 0& \quad \cdots& \quad \cdots& \quad 0& \quad p\\[3pt]0& \quad 1-p& \quad 0& \quad \cdots& \quad 0& \quad p\\[3pt]\vdots& \quad & \quad \ddots& \quad & \quad & \quad \vdots\\[3pt]\vdots& \quad & \quad & \quad \ddots& \quad & \quad \vdots\\[3pt]0& \quad \cdots& \quad \cdots& \quad 0& \quad 1-p& \quad p\end{pmatrix}\!.\]
The characteristic polynomial
![]() $\chi_{n,p} =\chi_{n,p} (z)$
of
$\chi_{n,p} =\chi_{n,p} (z)$
of
![]() $M_{n,p}$
satisfies
$M_{n,p}$
satisfies
and this recurrence relation can be deduced from a Laplace expansion of the first row of
![]() $M_{n,p}$
. It follows from
$M_{n,p}$
. It follows from
![]() $\chi_{1,p}(z)=z-p$
that
$\chi_{1,p}(z)=z-p$
that
We know that
![]() $\rho ( M_{n,p})$
is the largest zero of this polynomial in (0, 1).
$\rho ( M_{n,p})$
is the largest zero of this polynomial in (0, 1).
Acknowledgement
The author thanks Martin Zerner and Elmar Teufl for many helpful comments which improved the quality of this article. He is also grateful to the anonymous referee for several careful remarks.
Funding information
The author was financially supported via funds from the ERC Starting Grant 208417-NCIRW and by a PhD scholarship from the Landesgraduiertenforderung Baden-Württemberg.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.