Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T21:28:30.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimality of myopic stopping times for geometric discounting

Published online by Cambridge University Press:  14 July 2016

Bert Fristedt  and
Donald A. Berry
Bert Fristedt*
Affiliation:
University of Minnesota
Donald A. Berry*
Affiliation:
University of Minnesota
*
∗Postal address: School of Mathematics, 127 Vincent Hall, 206 Church Street SE, University of Minnesota, Minneapolis, MN 55455, USA.
∗∗Postal address: Department of Theoretical Statistics, 270 Vincent Hall, 206 Church Street SE, University of Minnesota, Minneapolis, MN 55455, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a sequence of conditionally independent Bernoulli random variables taking on the values 1 and − 1. The objective is to stop the sequence in order to maximize the discounted sum. Suppose the Bernoulli parameter has a beta distribution with integral parameters. It is optimal to stop when the conditional expectation of the next random variable is negative provided the discount factor is less than or equal to 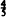. Moreover, 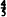is best possible. The case where the parameters of the beta distribution are arbitrary positive numbers is also treated.

Keywords

GAMBLINGBANDIT PROBLEMFUNDAMENTAL THEOREM OF GAMBLINGBETA DISTRIBUTIONS
Type
Short Communications
Information
Journal of Applied Probability , Volume 25 , Issue 2 , June 1988 , pp. 437 - 443
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partially supported by NSF grant DMS 86–03437.

Research partially supported by NSF grant DMS 85–05023.

References

Beckmann, M. J. (1973) Der diskontierte Bandit. OR-Verfahren XVIII, 9–18.Google Scholar
Berry, D. A. and Fristedt, B. (1985) Bandit Problems: Sequential Allocation of Experiments. Chapman and Hall, London.Google Scholar
Dubins, L. E. and Savage, L. J. (1976) Inequalities for Stochastic Processes: How to Gamble if You Must. Dover, New York.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and Its Applications , Vol. I, 3rd edition. Wiley, New York.Google Scholar
Fischer, J. (1979) Der diskontierte Einarmige Bandit. Metrika 26, 195–204.CrossRefGoogle Scholar
Glazebrook, K. D. and Jones, D. M. (1983) Some best possible results for a discounted one armed bandit. Metrika 30, 109–115.Google Scholar