Published online by Cambridge University Press: 15 August 2022
Let 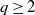 $q\ge2$
be an integer,
$q\ge2$
be an integer, 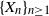 $\{X_n\}_{n\geq 1}$
a stochastic process with state space
$\{X_n\}_{n\geq 1}$
a stochastic process with state space 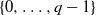 $\{0,\ldots,q-1\}$
, and F the cumulative distribution function (CDF) of
$\{0,\ldots,q-1\}$
, and F the cumulative distribution function (CDF) of 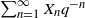 $\sum_{n=1}^\infty X_n q^{-n}$
. We show that stationarity of
$\sum_{n=1}^\infty X_n q^{-n}$
. We show that stationarity of 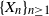 $\{X_n\}_{n\geq 1}$
is equivalent to a functional equation obeyed by F, and use this to characterize the characteristic function of X and the structure of F in terms of its Lebesgue decomposition. More precisely, while the absolutely continuous component of F can only be the uniform distribution on the unit interval, its discrete component can only be a countable convex combination of certain explicitly computable CDFs for probability distributions with finite support. We also show that
$\{X_n\}_{n\geq 1}$
is equivalent to a functional equation obeyed by F, and use this to characterize the characteristic function of X and the structure of F in terms of its Lebesgue decomposition. More precisely, while the absolutely continuous component of F can only be the uniform distribution on the unit interval, its discrete component can only be a countable convex combination of certain explicitly computable CDFs for probability distributions with finite support. We also show that 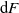 $\mathrm{d} F$
is a Rajchman measure if and only if F is the uniform CDF on [0, 1].
$\mathrm{d} F$
is a Rajchman measure if and only if F is the uniform CDF on [0, 1].