International Astronomical Union Colloquium, Pulsar Astronomy - 2000 and Beyond
- This volume was published under a former title. See this journal's title history.
Section B. High-Energy Emission
Part 6. Emission and Plasma Theory
High Energy Radiation from Pulsars
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 427-432
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Model of pulse separation in the gamma light curve of the Vela pulsar
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 433-434
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Beaming Due to Comptonisation in X-ray Pulsars
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 435-436
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A Ray-Tracing Model of the Vela Magnetosphere
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 437-438
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A model for the energetic emission from pulsars
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 439-440
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Thermal X-Ray Pulses Resulting From Pulsar Glitches
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 441-442
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Section C. Pair-Plasma Processes
Part 6. Emission and Plasma Theory
The Pair Cascade in Strong and Weak Field Pulsars
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 445-448
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Pulsar Death at an Advanced Age
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 449-454
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Pulsar Pair Plasma
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 455-456
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Pulsar Magnetospheres: Classical, Quasi-Classical and Quantum Descriptions
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 457-460
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Possible re-acceleration regions above the inner gap and pulsar gamma-ray emission
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 461-462
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Charge Densities above Pulsar Polar Caps
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 463-464
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Some Peculiaritiers of the Relativistic Electron-Positron Plasma Dynamics in the Pulsar Magnetosphere
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 465-468
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
ICS as a Limiting Factor for Electron Energies in Pulsar Magnetospheres
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 469-472
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Emission of particles and photons in the pulsar polar cap
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 473-478
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
High-energy accelerators above pulsar polar caps
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 479-480
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A full polar cap cascade model: pulsar γ-ray and X-ray luminosities
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 481-482
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Part 7. The Surrounding of Pulsars
Neutron Star/Supernova Remnant Associations
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 485-490
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Puzzling Pulsars and Supernova Remnants
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 491-492
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
1997 October Event(s) in the Crab Pulsar
-
- Published online by Cambridge University Press:
- 12 April 2016, pp. 493-498
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

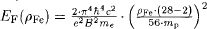 we obtain a value of
we obtain a value of 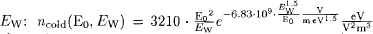 and
and  with
with  tells us, that
tells us, that 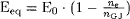 and hence the equilibrium density is:
and hence the equilibrium density is: