An asymptotic representation of low-frequency, linear, isentropic g-modes of a star is developed without the usual neglect of the Eulerian perturbation of the gravitational potential. Our asymptotic representation is based on the use of asymptotic expansions adequate for solutions of singular perturbation problems (see, e.g., Kevorkian & Cole 1981).
Linear, isentropic oscillation modes with frequency different from zero are governed by a fourth-order system of linear, homogeneous differential equations in the radial parts of the radial displacement ξ(r) and the divergence α(r). These equations take the form
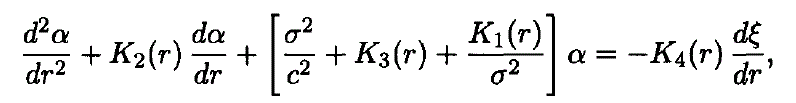
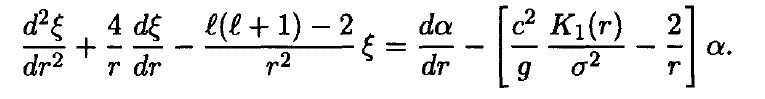
The symbols have their usual meaning. N2 is the square of the frequency of Brunt-Väisälä. The functions K1 (r), K2 (r), K3 (r), K4 (r), depend on the equilibrium model, e.g.,
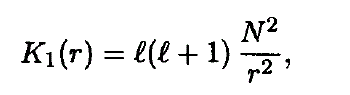
We introduce the small expansion parameter
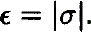
and assume, for the sake of simplification, N2 to be positive everywhere in the star so that the star is everywhere convectively stable.