Highlights of Astronomy, Highlights of Astronomy. As presented at the XXIVth General Assembly of the IAU, 2000
- This volume was published under a former title. See this journal's title history.
JD4: The Transneptunian Population
II. Joint Discussions
Dynamical Evolution of Trans-Neptunian Objects in High-Eccentricity Orbits
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 223-224
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Scattering of Planetesimals from Young Planetary Disks: Application to the β Pictoris System
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 225-228
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Composition of Comets and Interstellar Dust
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 229-232
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Comets and Circumstellar Dust
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 233-236
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Infrared Spectroscopy of the Centaur Asbolus with the ESO-Very Large Telescope
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 237-238
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A TNO Survey Project with the 2.2m Telescope at ESO La Silla
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 239-241
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Error Growth of the KS Regularized Orbital Motion
-
- Published online by Cambridge University Press:
- 30 March 2016, p. 242
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Effects of Multiple Planetary Encounters on Kuiper Belt Objects
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 243-244
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Census of the Kuiper-Belt Objects - The Taiwan-America Occultation Survey (TAOS)
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 245-246
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Evolution of the Edgeworth-Kuiper Belt
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 247-248
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Spectrophotometry of Trans-Neptunian Objects
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 249-250
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Resonant Gaps in the Scattered Cometary Population of the Trans-Neptunian Region
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 251-252
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Astrometry of Outer Solar System Bodies with Small Telescopes
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 253-254
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Statistical Ranging of Orbits for Trans-Neptunian Objects
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 255-256
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
JD5: Mixing and Diffusion in Stars: Theoretical Prediction and Observational Constraints
II. Joint Discussions
Joint Discussion 5 - Mixing and Diffusion in Stars: Introduction and Brief Overview
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 257-261
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Chemical Abundances in Main Sequence Stars
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 262-264
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Observations of Chemical Abundances in Stars: Globular Cluster Stars
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 265-269
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Special Case of ω Centauri
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 270-272
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Photometric Evidence for Mixing and Diffusion in GC Stars
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 273-275
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Rotational Braking, Angular Momentum Transport and the Light Element Abundances
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 276-278
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

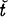 Observatory including our results. The extension of this programme using a new larger telescope is in preparation. We also mention a possibility of using some web tools for call for follow-up.
Observatory including our results. The extension of this programme using a new larger telescope is in preparation. We also mention a possibility of using some web tools for call for follow-up.