Report on Overlap Methods in Photographic Astrometry

Extract

The usual procedure for deriving standard coordinates ξ,η from the measured rectangular coordinates x, y of a star is to adopt a suitable model for the relationship between the measured x, y, magnitude m, color index c and the ξ, η. This relationship may, in general, be written as

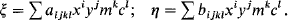
From the known standard coordinates ξ_r, η_r of some reference stars equally distributed over the plate area, the unknown plate constants a_ijkl, b_ijkl are found from a least-squares adjustment. After the adjustment the standard coordinates of each field star can be computed. In most cases a statistical criterion for the choice of the proper form of the above relationship between measured and standard coordinates may be useful because the systematic accuracy, obtained from the adjustment, may be seriously affected by the number of unknown parameters included. (Eichhorn et al., 1967). If the same star occurs on two or more plates, i.e. the plates being partly overlapped, one gets the final position by taking the mean of the individual positions on each plate. In this procedure, no direct account is taken of the ‘overlap’ in the equations of condition for the desired plate constants.