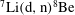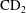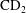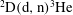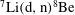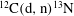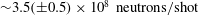1. Introduction
Recent rapid development of laser plasma accelerators has made it possible to accelerate protons and deuterons to high energies of approximately 70 and 170 MeV, respectively[Reference Gaillard, Kluge, Flippo, Bussmann, Gall, Lockard, Geissel, Offermann, Schollmeier, Sentoku and Cowan1, Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2]. These beams hitting a secondary target can create high-energy neutrons through, for example, ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$,
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$, ![]() ${}^{7}\mathrm{Li(p,n)}{}^{7}\mathrm{Be}$,
${}^{7}\mathrm{Li(p,n)}{}^{7}\mathrm{Be}$, ![]() ${}^{7}\mathrm{Li(d,xn)}{}^{8}\mathrm{Be}$,
${}^{7}\mathrm{Li(d,xn)}{}^{8}\mathrm{Be}$, ![]() ${}^{9}\mathrm{Be(p,n)}{}^{5}_{9}\mathrm{B}$, and
${}^{9}\mathrm{Be(p,n)}{}^{5}_{9}\mathrm{B}$, and ![]() ${}^{9}\mathrm{Be(d,n)}{}^{5}_{10}\mathrm{B}$ nuclear reactions[Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2–Reference Willingale, Petrov, Maksimchuk, Davis, Freeman, Joglekar, Matsuoka, Murphy, Ovchinnikov, Thomas, Van Woerkom and Krushelnick15]. Fast neutrons with energies in excess of 10 MeV resulting from the
${}^{9}\mathrm{Be(d,n)}{}^{5}_{10}\mathrm{B}$ nuclear reactions[Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2–Reference Willingale, Petrov, Maksimchuk, Davis, Freeman, Joglekar, Matsuoka, Murphy, Ovchinnikov, Thomas, Van Woerkom and Krushelnick15]. Fast neutrons with energies in excess of 10 MeV resulting from the ![]() ${}^{7}\mathrm{Li(d,xn)}{}^{8}\mathrm{Be}$ reaction (
${}^{7}\mathrm{Li(d,xn)}{}^{8}\mathrm{Be}$ reaction (![]() $Q=15.03\ \mathrm{MeV}$) have been reported by several authors[Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick6–Reference Davis and Petrov11]. Acceleration of deuterons is mostly reported in experiments using lasers with intensities of
$Q=15.03\ \mathrm{MeV}$) have been reported by several authors[Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick6–Reference Davis and Petrov11]. Acceleration of deuterons is mostly reported in experiments using lasers with intensities of ![]() $10^{19}\ \mathrm{W\ cm}^{-2}$. The deuterons are accelerated in focal spots on thin-film targets through either the target-normal sheath acceleration (TNSA) mechanism or the newly recognized break-out afterburner (BOA) mechanism[Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2]. There is another laser ignition of fusion (LIF) scheme for applications, based on the combination of ultra-high laser nonlinear force driven plasma blocks and the relativistic acceleration of ion blocks, which has shown how 70 MeV
$10^{19}\ \mathrm{W\ cm}^{-2}$. The deuterons are accelerated in focal spots on thin-film targets through either the target-normal sheath acceleration (TNSA) mechanism or the newly recognized break-out afterburner (BOA) mechanism[Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2]. There is another laser ignition of fusion (LIF) scheme for applications, based on the combination of ultra-high laser nonlinear force driven plasma blocks and the relativistic acceleration of ion blocks, which has shown how 70 MeV ![]() $\mathrm{D}^{+}$ and
$\mathrm{D}^{+}$ and ![]() $\mathrm{T}^{+}$ ions can be produced using of ps-laser pulses[Reference Moustaizis, Lalousis and Hora16]. The laser-driven bright sources of neutrons can be used in fusion material research[Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2, Reference Davis and Petrov11, Reference Perkins, Logan, Rosen, Perry, Diaz de la Rubia, Ghoniem, Ditmire, Springer and Wilks17] and proton beams in medical disciplines as hadron therapy for the treatment of cancer[Reference Banati, Hora, Lalousis and Moustaizis18].
$\mathrm{T}^{+}$ ions can be produced using of ps-laser pulses[Reference Moustaizis, Lalousis and Hora16]. The laser-driven bright sources of neutrons can be used in fusion material research[Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2, Reference Davis and Petrov11, Reference Perkins, Logan, Rosen, Perry, Diaz de la Rubia, Ghoniem, Ditmire, Springer and Wilks17] and proton beams in medical disciplines as hadron therapy for the treatment of cancer[Reference Banati, Hora, Lalousis and Moustaizis18].

Figure 1. (a) Diagram of the dual target configuration. (b) Configuration of scintillation detectors N1 to N5 around the target chamber.
In contrast to ultra-short high-intensity lasers which allow the generation of beams of protons and deuterons possessing kinetic energies ![]() ${\gg } 1\ \mathrm{MeV}$, sub-nanosecond lasers of the kJ-class capable of delivering a moderate intensity onto a target make it possible to accelerate ions up to MeV energies per nucleon[Reference Láska, Jungwirth, Krása, Krouský, Pfeifer, Rohlena, Ullschmied, Badziak, Parys, WoLowski, Gammino, Torrisi and Boody19–Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. The clear-cut evidence that the fastest protons accelerated by the laser system PALS (
${\gg } 1\ \mathrm{MeV}$, sub-nanosecond lasers of the kJ-class capable of delivering a moderate intensity onto a target make it possible to accelerate ions up to MeV energies per nucleon[Reference Láska, Jungwirth, Krása, Krouský, Pfeifer, Rohlena, Ullschmied, Badziak, Parys, WoLowski, Gammino, Torrisi and Boody19–Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. The clear-cut evidence that the fastest protons accelerated by the laser system PALS (![]() $1.315\ \mu \mathrm{m}$, 300 ps,
$1.315\ \mu \mathrm{m}$, 300 ps, ![]() $3\times 10^{16}\ \mathrm{W\ cm}^{-2}$) have energies up to
$3\times 10^{16}\ \mathrm{W\ cm}^{-2}$) have energies up to ![]() ${\sim } 4\ \mathrm{MeV}$[Reference Margarone, Krása, Giuffrida, Picciotto, Torrisi, Nowak, Musumeci, Velyhan, Prokůpek, Láska, Mocek, Ullschmied and Rus20, Reference Picciotto, Margarone, Bellutti, Colpo, Torrisi, Krása, Velyhan and Ullschmied21] creates a way to accelerate a high number of deuterons from the front side of a target and exploit them in the production of high-energy (
${\sim } 4\ \mathrm{MeV}$[Reference Margarone, Krása, Giuffrida, Picciotto, Torrisi, Nowak, Musumeci, Velyhan, Prokůpek, Láska, Mocek, Ullschmied and Rus20, Reference Picciotto, Margarone, Bellutti, Colpo, Torrisi, Krása, Velyhan and Ullschmied21] creates a way to accelerate a high number of deuterons from the front side of a target and exploit them in the production of high-energy (![]() ${\sim }15\ \mathrm{MeV}$) neutrons through the
${\sim }15\ \mathrm{MeV}$) neutrons through the ![]() ${}^{7}\mathrm{Li(d,xn)}$ nuclear reaction even if the mean kinetic energy of the bunch of deuterons is
${}^{7}\mathrm{Li(d,xn)}$ nuclear reaction even if the mean kinetic energy of the bunch of deuterons is ![]() ${<}$1 MeV. In addition, under these conditions up to
${<}$1 MeV. In addition, under these conditions up to ![]() $2\times 10^{8}$ neutrons per laser shot have be generated with the laser system PALS through the
$2\times 10^{8}$ neutrons per laser shot have be generated with the laser system PALS through the ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$ reaction, which is scalable with energy of other laser systems[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. This scheme is applicable to newly developed high-energy-class cryogenically cooled
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$ reaction, which is scalable with energy of other laser systems[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. This scheme is applicable to newly developed high-energy-class cryogenically cooled ![]() $\mathrm{Yb}^{3+}{:}\mathrm{YAG}$ multi-slab laser systems, allowing the production of a plasma with intensity
$\mathrm{Yb}^{3+}{:}\mathrm{YAG}$ multi-slab laser systems, allowing the production of a plasma with intensity ![]() $I\lambda ^{2}> 1\times 10^{16}\ \mu \mathrm{m}^{2}\ \mathrm{cm}^{-2}$[Reference Divoky, Sikocinski, Pilar, Lucianetti, Sawicka, Slezak and Mocek23].
$I\lambda ^{2}> 1\times 10^{16}\ \mu \mathrm{m}^{2}\ \mathrm{cm}^{-2}$[Reference Divoky, Sikocinski, Pilar, Lucianetti, Sawicka, Slezak and Mocek23].
A common phenomenon observed in experiments is the acceleration of protons coming from a contaminant layer on the irradiated surface of the target. The protons accelerated by the laser system PALS have a broad energy spectrum around a mean value of ![]() ${\sim }$2.5 MeV. Although the total cross section for neutron production through the
${\sim }$2.5 MeV. Although the total cross section for neutron production through the ![]() ${}^{7}\mathrm{Li(p,n)}$ reaction is only about three times lower than that for the
${}^{7}\mathrm{Li(p,n)}$ reaction is only about three times lower than that for the ![]() ${}^{7}\mathrm{Li(d,n)}$ reaction[Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick6], the neutron yield from the
${}^{7}\mathrm{Li(d,n)}$ reaction[Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick6], the neutron yield from the ![]() ${}^{7}\mathrm{Li(p,n)}$ reaction should be insignificant due to the very low content of protons in the produced plasma. Moreover, the peculiarity of the
${}^{7}\mathrm{Li(p,n)}$ reaction should be insignificant due to the very low content of protons in the produced plasma. Moreover, the peculiarity of the ![]() ${}^{7}\mathrm{Li(p,n)}$ reaction that for proton kinetic energies just above the production threshold the emitted neutrons are kinematically focused into a cone in the direction of the proton beam makes it difficult to distinguish them among other neutrons because of the very large divergence angle of the proton beam.
${}^{7}\mathrm{Li(p,n)}$ reaction that for proton kinetic energies just above the production threshold the emitted neutrons are kinematically focused into a cone in the direction of the proton beam makes it difficult to distinguish them among other neutrons because of the very large divergence angle of the proton beam.
In the experiment reported, a single planar deuterated polyethylene target was irradiated with the PALS laser, resulting in the production of neutrons through the ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$,
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$, ![]() ${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ nuclear reactions, as well as in acceleration of deuterons that were capable of initiating the
${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ nuclear reactions, as well as in acceleration of deuterons that were capable of initiating the ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction in a secondary LiF catcher target.
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction in a secondary LiF catcher target.
2. Experimental arrangement
A deuterated polyethylene target of 0.2 mm in thickness was exposed to a laser intensity of aapproximately ![]() $3\times 10^{16}\ \mathrm{W\ cm}^{-2}$ with the fundamental wavelength of
$3\times 10^{16}\ \mathrm{W\ cm}^{-2}$ with the fundamental wavelength of ![]() $1.315\ \mu \mathrm{m}$ delivered by the laser system PALS. The laser beam struck the
$1.315\ \mu \mathrm{m}$ delivered by the laser system PALS. The laser beam struck the ![]() $\mathrm{CD}_{2}$ target parallel to the target surface normal. The accelerated deuterons impacted a 1-mm-thick natural LiF slab with a surface area of
$\mathrm{CD}_{2}$ target parallel to the target surface normal. The accelerated deuterons impacted a 1-mm-thick natural LiF slab with a surface area of ![]() $17\ \mathrm{cm}^{2}$, which was positioned 10 cm off the primary
$17\ \mathrm{cm}^{2}$, which was positioned 10 cm off the primary ![]() $(\mathrm{CD}_{2})_{\mathrm{n}}$ target, as Figure 1 shows. The characteristics of the ions were measured using ion collectors (ICs) and a Thomson parabola spectrometer (TPS) positioned in the far expansion zone, i.e. outside the recombination zone. The emission of neutrons was observed by means of a calibrated temperature-compensated bubble dosimeters (BD-PND) with a sensitivity of
$(\mathrm{CD}_{2})_{\mathrm{n}}$ target, as Figure 1 shows. The characteristics of the ions were measured using ion collectors (ICs) and a Thomson parabola spectrometer (TPS) positioned in the far expansion zone, i.e. outside the recombination zone. The emission of neutrons was observed by means of a calibrated temperature-compensated bubble dosimeters (BD-PND) with a sensitivity of ![]() ${\sim }4\ \mathrm{b}\ \mu \mathrm{Sv}^{-1}$ (Bubble Technology Industries, Chalk River, Ontario, Canada KOJ 1J0) and five calibrated neutron time-of-flight (N-TOF) scintillation detectors composed of a fast plastic scintillator of BC408 type and of a photomultiplier tube[Reference Klir, Kravarik, Kubes, Rezac, Litseva, Tomaszewski, Karpinski, Paduch and Scholz24], which were positioned at distances of 1–3 m in various directions, as sketched in Figure 1. The BD-PND detectors were positioned inside and outside the target chamber to observe anisotropy in the neutron emission. To reduce the scintillator response to the gamma rays, the scintillation detectors were mounted inside a protective housing composed of 10-cm- thick interlocking lead bricks. The scintillation detectors were operated in a current mode.
${\sim }4\ \mathrm{b}\ \mu \mathrm{Sv}^{-1}$ (Bubble Technology Industries, Chalk River, Ontario, Canada KOJ 1J0) and five calibrated neutron time-of-flight (N-TOF) scintillation detectors composed of a fast plastic scintillator of BC408 type and of a photomultiplier tube[Reference Klir, Kravarik, Kubes, Rezac, Litseva, Tomaszewski, Karpinski, Paduch and Scholz24], which were positioned at distances of 1–3 m in various directions, as sketched in Figure 1. The BD-PND detectors were positioned inside and outside the target chamber to observe anisotropy in the neutron emission. To reduce the scintillator response to the gamma rays, the scintillation detectors were mounted inside a protective housing composed of 10-cm- thick interlocking lead bricks. The scintillation detectors were operated in a current mode.

Figure 2. (a) Typical time-resolved ion current density observed using an IC positioned at a distance of 1.5 m from a massive ![]() $\mathrm{CD}_{2}$ target in a backward direction at
$\mathrm{CD}_{2}$ target in a backward direction at ![]() $30^\circ $ with respect to the laser vector. The first peak was induced by XUV radiation. The peak at 70 ns was induced by 2.4 MeV protons. (b) Charge density of ions impacting on a secondary target at a distance of 10 cm for the
$30^\circ $ with respect to the laser vector. The first peak was induced by XUV radiation. The peak at 70 ns was induced by 2.4 MeV protons. (b) Charge density of ions impacting on a secondary target at a distance of 10 cm for the ![]() $\mathrm{CD}_{2}$ primary target, which was derived from the IC signal using the relationship (2). The dashed line shows the energy of deuterons. The laser irradiance on target was
$\mathrm{CD}_{2}$ primary target, which was derived from the IC signal using the relationship (2). The dashed line shows the energy of deuterons. The laser irradiance on target was ![]() ${\sim }3\times 10^{16}\ {\rm W\ cm}^{-2}$.
${\sim }3\times 10^{16}\ {\rm W\ cm}^{-2}$.
3. Results and discussion
When a ![]() $\mathrm{CD}_{2}$ thick foil target is irradiated with the PALS laser, neutrons are generated via
$\mathrm{CD}_{2}$ thick foil target is irradiated with the PALS laser, neutrons are generated via ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$ and
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$ and![]() ${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ nuclear reactions[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. The neutron yield per energy reaches a value up to
${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ nuclear reactions[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. The neutron yield per energy reaches a value up to ![]() ${\sim } 3.5\times 10^{5}\ \mathrm{neutrons/J}$ for an average laser energy of 550 J. This value equals the highest efficiency values observed at laser–solid interactions driven by high laser intensities ranging from
${\sim } 3.5\times 10^{5}\ \mathrm{neutrons/J}$ for an average laser energy of 550 J. This value equals the highest efficiency values observed at laser–solid interactions driven by high laser intensities ranging from ![]() $1\times 10^{18}$ to
$1\times 10^{18}$ to ![]() $5\times 10^{19}\ \mathrm{W\ cm}^{-2}$. Besides the neutrons, the laser-produced
$5\times 10^{19}\ \mathrm{W\ cm}^{-2}$. Besides the neutrons, the laser-produced ![]() $\mathrm{CD}_{2}$ plasma emits fast ions having energies of MeV, as Figure 2(a) shows. The time of flight value of 70 ns at a distance of 1.5 m corresponding to the peak induced by a group of fast protons indicates an energy of 2.4 MeV, while the maximum energy reaches a value of approximately 4 MeV. These protons are followed by deuterons, which impact the LiF catcher target traversing the distance between both the targets. It causes a delay in the emission of the neutrons from the D–Li reaction. The time needed to travel that distance can be determined from the TOF spectrum of ions obtained by transforming the IC signal to the TOF spectrum of the ion charge density:
$\mathrm{CD}_{2}$ plasma emits fast ions having energies of MeV, as Figure 2(a) shows. The time of flight value of 70 ns at a distance of 1.5 m corresponding to the peak induced by a group of fast protons indicates an energy of 2.4 MeV, while the maximum energy reaches a value of approximately 4 MeV. These protons are followed by deuterons, which impact the LiF catcher target traversing the distance between both the targets. It causes a delay in the emission of the neutrons from the D–Li reaction. The time needed to travel that distance can be determined from the TOF spectrum of ions obtained by transforming the IC signal to the TOF spectrum of the ion charge density:
where ![]() $q$ is the ion charge,
$q$ is the ion charge, ![]() $n_{\mathrm{IC}}(L,t)$ is the ion density,
$n_{\mathrm{IC}}(L,t)$ is the ion density, ![]() $j_{\mathrm{IC}}(L,t)$ is the ion current density observed at a distance
$j_{\mathrm{IC}}(L,t)$ is the ion current density observed at a distance ![]() $L$ from the primary target and
$L$ from the primary target and ![]() $ v$ is the ion velocity. We note that the ion current is commonly a sum of partial currents
$ v$ is the ion velocity. We note that the ion current is commonly a sum of partial currents ![]() $j_{i}$ of all the ionized species
$j_{i}$ of all the ionized species ![]() $j_{\mathrm{IC}}(L,t)=\Sigma j_{i}(L,t)$, including deuterons and carbon ions which are fully ionized as well as partially recombined. One of the partial currents is that of the protons, which originate from impurities on the front target surface. The partial currents can be revealed using a deconvolution of the TOF spectrum, as has been shown for a polyethylene plasma[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22, Reference Krása, Velyhan, Jungwirth, Krouský, Láska, Rohlena, Pfeifer and Ullschmied25].
$j_{\mathrm{IC}}(L,t)=\Sigma j_{i}(L,t)$, including deuterons and carbon ions which are fully ionized as well as partially recombined. One of the partial currents is that of the protons, which originate from impurities on the front target surface. The partial currents can be revealed using a deconvolution of the TOF spectrum, as has been shown for a polyethylene plasma[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22, Reference Krása, Velyhan, Jungwirth, Krouský, Láska, Rohlena, Pfeifer and Ullschmied25].

Figure 3. Scintillation detector signal induced by emission of ![]() $\gamma $ radiation and neutrons produced via
$\gamma $ radiation and neutrons produced via ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$,
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$, ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$, and
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$, and ![]() ${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ nuclear reactions. The emission was observed in the radial direction N3 (see Figure 1) at a distance of 230 cm from the target (shot #44511).
${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ nuclear reactions. The emission was observed in the radial direction N3 (see Figure 1) at a distance of 230 cm from the target (shot #44511).
Using a similarity relationship for ![]() $\rho $ detected by identical detectors placed at two different distances
$\rho $ detected by identical detectors placed at two different distances ![]() $L_{1}$ and
$L_{1}$ and ![]() $L_{2}$ in the same direction[Reference Krása, Parys, Velardi, Velyhan, Ryć, Delle Side and Nassisi26]
$L_{2}$ in the same direction[Reference Krása, Parys, Velardi, Velyhan, Ryć, Delle Side and Nassisi26]
where ![]() $L_{1}/t_{1}=L_{2}/t_{2}$, we can determine a time-resolved ion charge density
$L_{1}/t_{1}=L_{2}/t_{2}$, we can determine a time-resolved ion charge density ![]() $\rho (L_{2},t_{2})$ at a chosen distance
$\rho (L_{2},t_{2})$ at a chosen distance ![]() $L_{2}$ when
$L_{2}$ when ![]() $\rho (L_{1},t_{1})$ is observed at a distance
$\rho (L_{1},t_{1})$ is observed at a distance ![]() $L_{1}$. The validity of the relationship (2) is limited for distances beyond some critical distance from the target,
$L_{1}$. The validity of the relationship (2) is limited for distances beyond some critical distance from the target, ![]() $L_{\mathrm{cr}}$, where the three-body recombination becomes insignificant due to the plasma rarefaction, the expanding ions have frozen charge states and their total charge
$L_{\mathrm{cr}}$, where the three-body recombination becomes insignificant due to the plasma rarefaction, the expanding ions have frozen charge states and their total charge ![]() $Q_{0}$ can be regarded as constant[Reference Lorusso, Krása, Rohlena, Nassisi, Belloni and Doria27]. The value of
$Q_{0}$ can be regarded as constant[Reference Lorusso, Krása, Rohlena, Nassisi, Belloni and Doria27]. The value of ![]() $L_{\mathrm{cr}}$ depends on the laser irradiance on the target and the target material; in this experiment
$L_{\mathrm{cr}}$ depends on the laser irradiance on the target and the target material; in this experiment ![]() $L_{\mathrm{cr}} < 50\ {\rm cm}$. It is evident that the transformation of
$L_{\mathrm{cr}} < 50\ {\rm cm}$. It is evident that the transformation of ![]() $\rho (L,t)$ to a short distance
$\rho (L,t)$ to a short distance ![]() $L_{\mathrm{s}} < L_{\mathrm{cr}}$ gives underestimated values of the ion charge density due to the three-body recombination in this area. Although the ICs can hardly be used at a short distance from the target due to harmful effects caused by both the electrical breakdown of IC initiated by the collected current with a density of
$L_{\mathrm{s}} < L_{\mathrm{cr}}$ gives underestimated values of the ion charge density due to the three-body recombination in this area. Although the ICs can hardly be used at a short distance from the target due to harmful effects caused by both the electrical breakdown of IC initiated by the collected current with a density of ![]() ${\sim } 100\ \mathrm{A\ cm}^{-2}$ and the strong electromagnetic pulse (EMP) interference[Reference De Marco, Pfeifer, Krousky, Krasa, Cikhardt, Klir and Nassisi28], the use of a passive detector, e.g., solid state track detector stacks, may partially solve the problem. Nevertheless, the obtained time-resolved density of charges
${\sim } 100\ \mathrm{A\ cm}^{-2}$ and the strong electromagnetic pulse (EMP) interference[Reference De Marco, Pfeifer, Krousky, Krasa, Cikhardt, Klir and Nassisi28], the use of a passive detector, e.g., solid state track detector stacks, may partially solve the problem. Nevertheless, the obtained time-resolved density of charges ![]() $\rho (L,t)$ impinging on a catcher target provides an acceptable approximation of the flight times of deuterons to the LiF target, as Figure 2(b) shows. Two dominating peaks corresponding to the deuteron energy of
$\rho (L,t)$ impinging on a catcher target provides an acceptable approximation of the flight times of deuterons to the LiF target, as Figure 2(b) shows. Two dominating peaks corresponding to the deuteron energy of ![]() ${\sim }$400 and
${\sim }$400 and ![]() $\sim $200 keV are characteristic for the time-resolved charge density of ions.
$\sim $200 keV are characteristic for the time-resolved charge density of ions.

Figure 4. (a) Geometry of a nuclear reaction in the laboratory frame in which an incident deuteron with energy ![]() $E_{\mathrm{D}}$ impinges on a Li atom of the stationary LiF target and angular distribution of the neutron energy calculated for a value
$E_{\mathrm{D}}$ impinges on a Li atom of the stationary LiF target and angular distribution of the neutron energy calculated for a value ![]() $Q=15.03\ {\rm MeV}$ of the
$Q=15.03\ {\rm MeV}$ of the ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction. (b) Deuteron energy dependence of the energy of d–Li neutrons detected in chosen directions as calculated using formula (1) in [Reference Petrov, Higginson, Davis, Petrova, McGuffey, Qiao and Beg10] describing the kinematics of neutron production in binary collisions between a projectile and an atom in a stationary target.
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction. (b) Deuteron energy dependence of the energy of d–Li neutrons detected in chosen directions as calculated using formula (1) in [Reference Petrov, Higginson, Davis, Petrova, McGuffey, Qiao and Beg10] describing the kinematics of neutron production in binary collisions between a projectile and an atom in a stationary target.
A typical signal of the scintillation detector that is induced by ![]() $\gamma $ radiation and neutrons coming from nuclear reactions
$\gamma $ radiation and neutrons coming from nuclear reactions ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$,
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$, ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$,
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$, ![]() ${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ is shown in Figure 3.
${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ is shown in Figure 3.
In contrast to the zero time coordinate for neutrons from the ![]() $\mathrm{D(d,n)}{}^{3}\mathrm{He}$ and
$\mathrm{D(d,n)}{}^{3}\mathrm{He}$ and ![]() ${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ reactions, which is related to the TOF of gamma radiation, the determination of the start time of neutrons produced via the
${}^{12}\mathrm{C(d,n)}{}^{13}\mathrm{N}$ reactions, which is related to the TOF of gamma radiation, the determination of the start time of neutrons produced via the ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction is encumbered by uncertainty caused by the broadband TOF spectrum of deuterons impinging on the LiF catcher target. A way to minimize this uncertainty consists of calculations of flight times
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction is encumbered by uncertainty caused by the broadband TOF spectrum of deuterons impinging on the LiF catcher target. A way to minimize this uncertainty consists of calculations of flight times ![]() $\mbox{TOF}_{\mathrm{D}}$ of deuterons to the LiF catcher target and flight times
$\mbox{TOF}_{\mathrm{D}}$ of deuterons to the LiF catcher target and flight times ![]() $\mbox{N-TOF}_{\mbox{D--Li}}$ of D–Li neutrons to the scintillation detectors. The value of
$\mbox{N-TOF}_{\mbox{D--Li}}$ of D–Li neutrons to the scintillation detectors. The value of ![]() $\mbox{N-TOF}_{\mbox{D--Li}}$ can be determined using formulae describing the kinematics of neutron production in binary collisions between a projectile and an atom in a stationary target, such as those derived and discussed in[Reference Petrov, Higginson, Davis, Petrova, McGuffey, Qiao and Beg10, Reference Izumi, Sentoku, Habara, Takahashi, Ohtani, Sonomoto, Kodama, Norimatsu, Fujita, Kitagawa, Mima, Tanaka and Yamanaka29]. The dependence of neutron energy on the energy of deuterons and on the direction of observation is shown in Figure 4.
$\mbox{N-TOF}_{\mbox{D--Li}}$ can be determined using formulae describing the kinematics of neutron production in binary collisions between a projectile and an atom in a stationary target, such as those derived and discussed in[Reference Petrov, Higginson, Davis, Petrova, McGuffey, Qiao and Beg10, Reference Izumi, Sentoku, Habara, Takahashi, Ohtani, Sonomoto, Kodama, Norimatsu, Fujita, Kitagawa, Mima, Tanaka and Yamanaka29]. The dependence of neutron energy on the energy of deuterons and on the direction of observation is shown in Figure 4.
Figure 5 shows the arrival time of neutrons, ![]() $t_{\mathrm{N}}$, related to the time of the beam–target interaction, which is the sum of the time of flight
$t_{\mathrm{N}}$, related to the time of the beam–target interaction, which is the sum of the time of flight ![]() $\mbox{TOF}_{\mathrm{D}}$ of deuterons to the catcher LiF target and the time of flight
$\mbox{TOF}_{\mathrm{D}}$ of deuterons to the catcher LiF target and the time of flight ![]() $\mbox{N-TOF}_{\mbox{D--Li}}$ of
$\mbox{N-TOF}_{\mbox{D--Li}}$ of ![]() ${}^{7}\mathrm{Li(d,n)}^{8}\mathrm{Be}$ neutrons from the LiF target to the scintillation detectors:
${}^{7}\mathrm{Li(d,n)}^{8}\mathrm{Be}$ neutrons from the LiF target to the scintillation detectors:

Figure 5. Deuteron energy dependence of the neutron arrival time at detectors N1–N5 (see Figure 4) related to the laser–target interaction. The distances from the catcher LiF target to the scintillation detectors were ![]() $L_{\mathrm{N1}}=1.81\ {\rm m}$,
$L_{\mathrm{N1}}=1.81\ {\rm m}$, ![]() $L_{\mbox{N2--4}}=2.28\mbox{--}2.41\ {\rm m}$, and
$L_{\mbox{N2--4}}=2.28\mbox{--}2.41\ {\rm m}$, and ![]() $L_{\mathrm{N5}}= 0.85\ {\rm m}$.
$L_{\mathrm{N5}}= 0.85\ {\rm m}$.
Figure 6 shows the scintillation detector signals observed at five different distances and directions N1 to N5 with respect to the mean direction of deuterons impinging on the LiF target (see Figures 1 and 4). Using the dependence of the arrival times of neutrons on the energy of deuterons, ![]() $E_{\mathrm{D}}$, we can interpret individual maxima or partial peaks in the scintillation detector signals. The maxima in the signals shown in figure 6 may be sorted into two groups with respect to the energy of deuterons:
$E_{\mathrm{D}}$, we can interpret individual maxima or partial peaks in the scintillation detector signals. The maxima in the signals shown in figure 6 may be sorted into two groups with respect to the energy of deuterons: ![]() $E_{\mbox{D-1}}\cong 400\ {\rm keV}$ (N1 – 52 ns, N2 – 64 ns, N4 – 60 ns, N5 – 33 ns) and
$E_{\mbox{D-1}}\cong 400\ {\rm keV}$ (N1 – 52 ns, N2 – 64 ns, N4 – 60 ns, N5 – 33 ns) and ![]() $E_{\mbox{D-2}}\cong 200\ {\rm keV}$ (N1 – 59 ns, N2 – 64 ns, N3 – 68 ns, N5 – 41 ns). The beginnings of all the signals N1 – N5 correspond to a deuteron energy of
$E_{\mbox{D-2}}\cong 200\ {\rm keV}$ (N1 – 59 ns, N2 – 64 ns, N3 – 68 ns, N5 – 41 ns). The beginnings of all the signals N1 – N5 correspond to a deuteron energy of ![]() ${\sim }$1 MeV. The 400 keV deuterons induce a peak in the time-resolved ion charge density at
${\sim }$1 MeV. The 400 keV deuterons induce a peak in the time-resolved ion charge density at ![]() ${\sim }$16 ns for a distance of 10 cm, and the second group of deuterons with
${\sim }$16 ns for a distance of 10 cm, and the second group of deuterons with ![]() $E_{\mbox{D-2}} \sim 200\ {\rm keV}$ create a peak at
$E_{\mbox{D-2}} \sim 200\ {\rm keV}$ create a peak at ![]() ${\sim }$23 ns, which is the second highest one. The occurrence of protons and deuterons with energy
${\sim }$23 ns, which is the second highest one. The occurrence of protons and deuterons with energy ![]() $>$1.9 and 2.4 MeV, respectively, was confirmed by the tracks observed on a CR-39 track detector protected with an Al foil of
$>$1.9 and 2.4 MeV, respectively, was confirmed by the tracks observed on a CR-39 track detector protected with an Al foil of ![]() $40\ \mu {\rm m}$ in thickness. The number of these ions was estimated to be
$40\ \mu {\rm m}$ in thickness. The number of these ions was estimated to be ![]() ${\sim } 10^{12}$ per shot. The contribution of MeV deuterons to the neutron generation was insignificant.
${\sim } 10^{12}$ per shot. The contribution of MeV deuterons to the neutron generation was insignificant.
Sorting of the peaks in the scintillation detector signals indicates that the repetitive bursts observed in the emission of fast ions in sub-nanosecond laser–solid experiments[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22] may give rise to bursts in emission of fast neutrons generated via the beam–target ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction. Clear evidence is given by the observed well-separated maxima, for example at 52 and 59 ns in the N1 signal, and also at 60 and 78 ns in the N4 signal, that correlate well with the peaks of 200 and 400 keV deuterons appearing in the time dependence of the ion charge density (see Figure 2(b)).
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reaction. Clear evidence is given by the observed well-separated maxima, for example at 52 and 59 ns in the N1 signal, and also at 60 and 78 ns in the N4 signal, that correlate well with the peaks of 200 and 400 keV deuterons appearing in the time dependence of the ion charge density (see Figure 2(b)).
The energy of the observed neutrons depends not only on the kinetic energy of fusing deuterons, but also on the direction of observation. Most of the neutrons emitted in the forward direction with respect to the direction of impinging deuterons have energy ![]() ${>}14\ {\rm MeV}$. Only a minority of them can reach
${>}14\ {\rm MeV}$. Only a minority of them can reach ![]() ${\sim }$16 MeV energy. The maximum neutron yield from both the primary and secondary reactions was
${\sim }$16 MeV energy. The maximum neutron yield from both the primary and secondary reactions was ![]() $3.5\times 10^{8}$ neutrons per shot. The partial contributions of both the
$3.5\times 10^{8}$ neutrons per shot. The partial contributions of both the ![]() $\mathrm{D(d,n)}^{3}\mathrm{He}$ and
$\mathrm{D(d,n)}^{3}\mathrm{He}$ and ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reactions can be estimated from the scintillation detector signal, by taking into account the dependence of the scintillation intensity on the energy deposited by neutrons. If we consider the solid angle of the expanding plasma plume containing the fast deuterons[Reference Krása, Velyhan, Jungwirth, Krouský, Láska, Rohlena, Pfeifer and Ullschmied25] reduced by the solid angle of the laser beam, because the deuterons are emitted from the front target surface, the possible maximum yield could be as high as
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ reactions can be estimated from the scintillation detector signal, by taking into account the dependence of the scintillation intensity on the energy deposited by neutrons. If we consider the solid angle of the expanding plasma plume containing the fast deuterons[Reference Krása, Velyhan, Jungwirth, Krouský, Láska, Rohlena, Pfeifer and Ullschmied25] reduced by the solid angle of the laser beam, because the deuterons are emitted from the front target surface, the possible maximum yield could be as high as ![]() $Y_{\mbox{D--Li,max}}\sim 2\times 10^{8}\ \mathrm{neutrons\ sr}^{-1}$. This value is more or less comparable to the value of
$Y_{\mbox{D--Li,max}}\sim 2\times 10^{8}\ \mathrm{neutrons\ sr}^{-1}$. This value is more or less comparable to the value of ![]() $Y_{\mbox{D--Li}}=8\times 10^{8}\ \mathrm{neutrons\ sr}^{-1}$ of the
$Y_{\mbox{D--Li}}=8\times 10^{8}\ \mathrm{neutrons\ sr}^{-1}$ of the ![]() ${}^{7}\mathrm{Li(d,xn)}$ nuclear reaction driven by an intensity of
${}^{7}\mathrm{Li(d,xn)}$ nuclear reaction driven by an intensity of![]() $2\times 10^{19}\ \mathrm{W\ cm}^{-2}$[Reference Higginson, McNaney, Swift, Petrov, Davis, Frenje, Jarrott, Kodama, Lancaster, Mackinnon, Nakamura, Patel, Tynan and Beg7]. In that work the deuterons were produced using the Titan laser (energy 360 J and pulse length 9 ps) and accelerated from the rear surface of the foil through the TNSA mechanism. It follows from this comparison that different power-law relations govern both the experiments. Moreover, the similarity parameter
$2\times 10^{19}\ \mathrm{W\ cm}^{-2}$[Reference Higginson, McNaney, Swift, Petrov, Davis, Frenje, Jarrott, Kodama, Lancaster, Mackinnon, Nakamura, Patel, Tynan and Beg7]. In that work the deuterons were produced using the Titan laser (energy 360 J and pulse length 9 ps) and accelerated from the rear surface of the foil through the TNSA mechanism. It follows from this comparison that different power-law relations govern both the experiments. Moreover, the similarity parameter ![]() $I\lambda ^{2}$ does not also fully scale the generation of DD neutrons driven by high-power lasers with femtosecond to nanosecond pulse durations[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. Thus, not only the laser intensity, but also the nonlinear phenomena occurring affect the laser energy absorption by the generated plasma and, thus, the ion acceleration.
$I\lambda ^{2}$ does not also fully scale the generation of DD neutrons driven by high-power lasers with femtosecond to nanosecond pulse durations[Reference Krása, Klír, Velyhan, Margarone, Krouský, Jungwirth, Skála, Pfeifer, Kravárik, Kubeš, Řezáč and Ullschmied22]. Thus, not only the laser intensity, but also the nonlinear phenomena occurring affect the laser energy absorption by the generated plasma and, thus, the ion acceleration.
Both the analysis of the N-TOF spectra and time-resolved ion charge density of the produced ions have shown that deuterons induced the ![]() ${}^{7}\mathrm{Li(d,n)}$ nuclear reaction while possessing kinetic energy
${}^{7}\mathrm{Li(d,n)}$ nuclear reaction while possessing kinetic energy ![]() $E_{\mathrm{d}} < 1\ {\rm MeV}$. Under these conditions the neutron source becomes isotropic[Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick6]. A number of neutron detectors used contemporaneously at various directions and distances allow an evaluation of the anisotropy in the neutron emission. Nevertheless, our previous measurement of fusion neutron spectra outside the plasma focus device PF-1000 demonstrated the significant influence of the plasma vessel on the primary spectrum of generated neutrons[Reference Králík, Krása, Velyhan, Scholz, Ivanova-Stanik, Bienkowska, Miklaszewski, Schmidt, Řezáč, Klír, Kravárik and Kubeš30]. Considering also shot-to-shot fluctuations in the ion emission[Reference Krása, Velyhan, Margarone, Krouský, Láska, Jungwirth, Rohlena, Ullschmied, Parys, Ryć and Wołowski31], more complex laboratory equipment is needed to measure anisotropy in neutron emission through the beam–target reaction.
$E_{\mathrm{d}} < 1\ {\rm MeV}$. Under these conditions the neutron source becomes isotropic[Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick6]. A number of neutron detectors used contemporaneously at various directions and distances allow an evaluation of the anisotropy in the neutron emission. Nevertheless, our previous measurement of fusion neutron spectra outside the plasma focus device PF-1000 demonstrated the significant influence of the plasma vessel on the primary spectrum of generated neutrons[Reference Králík, Krása, Velyhan, Scholz, Ivanova-Stanik, Bienkowska, Miklaszewski, Schmidt, Řezáč, Klír, Kravárik and Kubeš30]. Considering also shot-to-shot fluctuations in the ion emission[Reference Krása, Velyhan, Margarone, Krouský, Láska, Jungwirth, Rohlena, Ullschmied, Parys, Ryć and Wołowski31], more complex laboratory equipment is needed to measure anisotropy in neutron emission through the beam–target reaction.
4. Conclusions
The deuterons generated on the front side of a thick ![]() $\mathrm{CD}_{2}$ foil exposed to an intensity of
$\mathrm{CD}_{2}$ foil exposed to an intensity of ![]() ${\sim } 3\times 10^{16}\ \mathrm{W\ cm}^{-2}$ using the PALS laser system were exploited as drivers of the
${\sim } 3\times 10^{16}\ \mathrm{W\ cm}^{-2}$ using the PALS laser system were exploited as drivers of the ![]() ${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ nuclear fusion reaction. The deuterons accelerated in the backward direction impinged on a LiF secondary target with an energy of 200–400 keV and produced D–Li neutrons with energies
${}^{7}\mathrm{Li(d,n)}{}^{8}\mathrm{Be}$ nuclear fusion reaction. The deuterons accelerated in the backward direction impinged on a LiF secondary target with an energy of 200–400 keV and produced D–Li neutrons with energies ![]() $>$14 MeV. Since only a small fraction of fast deuterons were hitting the LiF catcher target used, the maximum yield of D–D and D–Li neutrons was
$>$14 MeV. Since only a small fraction of fast deuterons were hitting the LiF catcher target used, the maximum yield of D–D and D–Li neutrons was ![]() ${\sim } 3.5\times 10^{8}\ \mathrm{neutrons/shot}$, which gives the normalized yield of
${\sim } 3.5\times 10^{8}\ \mathrm{neutrons/shot}$, which gives the normalized yield of ![]() ${\sim }5.8\times 10^{5}\ \mathrm{neutrons/J}$. This value should still increase when increasing the area of the LiF target catcher.
${\sim }5.8\times 10^{5}\ \mathrm{neutrons/J}$. This value should still increase when increasing the area of the LiF target catcher.
Acknowledgements
The authors gratefully acknowledge the support of the staff of the PALS laser facility without whose assistance this work would not have been possible. The research leading to these results has received funding from the Czech Science Foundation (Grant No. P205/12/0454), the Czech Republic’s Ministry of Education, Youth and Sports (Project No. LM2010014), LASERLAB-EUROPE (grant agreement no 284464, EC’s Seventh Framework Programme) and the European Social Fund and state budget of the Czech Republic (Project No. CZ.1.07/2.3.00/20.0279).