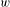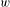1. Introduction
Inertial confinement fusion (ICF) is a concept for an alternative energy source, which releases energy by compressing a millimeter-scale capsule containing fusion fuel (i.e., hydrogen isotopes such as tritium, T, and deuterium, D), with ablation pressure driven by high power lasers[Reference Nuckolls, Wood, Thiessen and Zimmerman1, Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter2]. Substantial progress has been made in theory, experiment and diagnostics of ICF, but efficient fuel burn, ignition, has not yet been achieved due to discrepancies between experiments and simulations[Reference Lindl, Landen, Edwards, Moses and Team3]. While the sources of discrepancies have been extensively investigated and many of them have been recognized[Reference Clark, Marinak, Weber, Eder, Haan, Hammel, Hinkel, Jones, Milovich, Patel, Robey, Salmonson, Sepke and Thomas4], diagnostics that directly observe the evolution of the ICF implosion plasma spatial structure are desired to advance ICF science toward ignition.
Multi-monochromatic x-ray imagers (MMIs) are attractive instruments for this purpose. The MMI is a unique 2D spectrometer consisting of a pinhole array (PHA), a multi-layered mirror (MLM) and a microchannel plate (MCP)[Reference Koch, Barbee, Izumi, Tommasini, Mancini, Welser and Marshall5, Reference Tommasini, Koch, Izumi, Welser, Mancini, Delettrez, Regan and Smalyuk6]. It records an array of ICF implosion core images, each of which is formed by photons of slightly different wavelength. By processing MMI data, one can extract narrow-band images (i.e., intensity images of narrow spectral ranges), space-integrated spectra[Reference Welser, Mancini, Koch, Dalhed, Lee, Golovkin, Marshall, Delettrez and Klein7–Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9] and 2D space-resolved spectra[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10]. Spectroscopic analysis of the images and spectra extracted from the MMI data can provide a variety of approaches to constrain the ICF plasma spatial structure in electron temperature, ![]() $T_{e}$, and electron density,
$T_{e}$, and electron density, ![]() $n_{e}$.
$n_{e}$.
For example, we added a small amount of Ar into ![]() $\text{D}_{2}$ fuel as a tracer and analyzed the Ar line emission to characterize the
$\text{D}_{2}$ fuel as a tracer and analyzed the Ar line emission to characterize the ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ of the core. Previously, we extracted time-resolved 2D
$n_{e}$ of the core. Previously, we extracted time-resolved 2D ![]() $T_{e}$ maps from two narrow-band images[Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan, Smalyuk, Welser-Sherrill and Golovkin11]. From a collection of space-resolved spectra, we extracted time-resolved 2D
$T_{e}$ maps from two narrow-band images[Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan, Smalyuk, Welser-Sherrill and Golovkin11]. From a collection of space-resolved spectra, we extracted time-resolved 2D ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ maps[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10]. Synthetic investigations also suggest that time-resolved 3D
$n_{e}$ maps[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10]. Synthetic investigations also suggest that time-resolved 3D ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ spatial distributions of ICF cores can be extracted by simultaneously analyzing collections of 2D space-resolved spectra extracted from three MMI instruments fielded along quasi-orthogonal lines of sight[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12]. Thus, MMI diagnostics have the potential to better constrain ICF experiments and advance ICF theory.
$n_{e}$ spatial distributions of ICF cores can be extracted by simultaneously analyzing collections of 2D space-resolved spectra extracted from three MMI instruments fielded along quasi-orthogonal lines of sight[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12]. Thus, MMI diagnostics have the potential to better constrain ICF experiments and advance ICF theory.
While MMI data are rich in information, MMI data with good signal do not necessarily provide reliable information. To realize reliable MMI diagnostics, it is important to efficiently sample an object’s spatial information. This requires the MMI setup to be optimized for every application.
In this paper, we discuss a criterion for reliable MMI diagnostics and show how this criterion affects the reliability of the extracted spatial information by reconstructing narrow-band images from synthetic MMI data. It is difficult to experimentally study the fidelity of the reconstructed images because what is expected of the image is not known a priori. These questions can be best addressed using synthetic MMI data since the expected images can be computed. We show that the PHA tilt must be optimized to efficiently sample object spatial information and to minimize the minimum spectral width, ![]() $w$, required for the image reconstruction. This reconstruction width has to be significantly narrower than the full width at half maximum (FWHM) of the diagnostic lines.
$w$, required for the image reconstruction. This reconstruction width has to be significantly narrower than the full width at half maximum (FWHM) of the diagnostic lines.
This paper is organized as follows. Section 2 shows MMI data obtained with appropriate and inappropriate pinhole array designs and defines the criterion for reliable MMI diagnostics. Section 3 discusses the spectral model, which is used to create synthetic MMI data and also to compute expected images. In Section 4, the impact of the criterion is synthetically investigated using these models. The conclusions are given in Section 5.
2. PHA design and image reconstruction
The MMI consists of a hexagonally allocated PHA, a MLM and a MCP (Figure 1(a)), which provide 2D spatial resolution (![]() ${\rm\Delta}x\approx 11~{\rm\mu}\text{m}$), spectral resolution (
${\rm\Delta}x\approx 11~{\rm\mu}\text{m}$), spectral resolution (![]() $E/{\rm\Delta}E\approx 150$) and time resolution (
$E/{\rm\Delta}E\approx 150$) and time resolution (![]() ${\rm\Delta}t\approx 100~\text{ps}$), respectively. The given resolutions are typical values for our applications[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10–Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12]. The spatial resolution depends on pinhole size and object–PHA–detector distances. The spectral and temporal resolutions are determined by the specifications of the MLM and MCP, respectively. A key component for successful MMI data measurement is the PHA design, and it has to be optimized for every application. Here, we discuss necessary considerations to optimize the PHA design through the application to Ar-doped ICF experiments.
${\rm\Delta}t\approx 100~\text{ps}$), respectively. The given resolutions are typical values for our applications[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10–Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12]. The spatial resolution depends on pinhole size and object–PHA–detector distances. The spectral and temporal resolutions are determined by the specifications of the MLM and MCP, respectively. A key component for successful MMI data measurement is the PHA design, and it has to be optimized for every application. Here, we discuss necessary considerations to optimize the PHA design through the application to Ar-doped ICF experiments.

Figure 1. (a) The MMI consists of a PHA, a MLM and a MCP. The signal collected through a pinhole is proportional to the source-to-pinhole solid angle, ![]() ${\rm\Omega}={\it\pi}D^{2}/4p^{2}$. (b) The spatial resolution is determined by the object–pinhole–detector distances. (c) The magnification is determined by the object–pinhole distance,
${\rm\Omega}={\it\pi}D^{2}/4p^{2}$. (b) The spatial resolution is determined by the object–pinhole–detector distances. (c) The magnification is determined by the object–pinhole distance, ![]() $p$, and the object–detector distance,
$p$, and the object–detector distance, ![]() $L$. The optimal pinhole separation,
$L$. The optimal pinhole separation, ![]() $l$, is determined so that images of size
$l$, is determined so that images of size ![]() $\mathit{FM}$ do not overlap.
$\mathit{FM}$ do not overlap.
Pinhole size is determined based on the expected signal levels on the detector and the desired spatial resolution. The expected signal level on the detector depends on the object radiation power, the pinhole size, the object–PHA–detector distances and the detector sensitivity. For example, when the ICF implosion core is diagnosed with signals from Ar tracer, the core radiation power needs to be estimated with a spectral model at ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ predicted from the hydrodynamic simulations. If the estimated signals seem too low for a given configuration, one can increase the signals on the detector by increasing the object radiation power, increasing the object solid angle to the pinhole or improving the detector sensitivity. In our application, we field the instrument with a fixed PHA–detector distance as close as possible to the object and use the x-ray framing camera available at OMEGA. This leaves us only two options for increasing the signal levels on the detector: (1) increasing the object solid angle to the pinhole by increasing the pinhole size (the blow-up in Figure 1(a)) or (2) increasing the object radiation power by increasing the Ar tracer amount. One must consider the trade-off due to these options. For example, as the pinhole size is increased, the spatial resolution deteriorates because the signals observed at every point on the detector are integrated over a larger area on the source, as illustrated in Figure 1(b). When the Ar fraction is increased, one has to consider its effects on the implosion hydrodynamics[Reference MacFarlane, Golovkin, Mancini, Welser, Bailey, Koch, Mehlhorn, Rochau, Wang and Woodruff13]. The pinhole size needs to be optimized taking these details into account.
$n_{e}$ predicted from the hydrodynamic simulations. If the estimated signals seem too low for a given configuration, one can increase the signals on the detector by increasing the object radiation power, increasing the object solid angle to the pinhole or improving the detector sensitivity. In our application, we field the instrument with a fixed PHA–detector distance as close as possible to the object and use the x-ray framing camera available at OMEGA. This leaves us only two options for increasing the signal levels on the detector: (1) increasing the object solid angle to the pinhole by increasing the pinhole size (the blow-up in Figure 1(a)) or (2) increasing the object radiation power by increasing the Ar tracer amount. One must consider the trade-off due to these options. For example, as the pinhole size is increased, the spatial resolution deteriorates because the signals observed at every point on the detector are integrated over a larger area on the source, as illustrated in Figure 1(b). When the Ar fraction is increased, one has to consider its effects on the implosion hydrodynamics[Reference MacFarlane, Golovkin, Mancini, Welser, Bailey, Koch, Mehlhorn, Rochau, Wang and Woodruff13]. The pinhole size needs to be optimized taking these details into account.
The pinholes are arranged in a hexagonal pattern because this allows the object images to fill the detector plane most efficiently. The pinhole separation, ![]() $l$, is optimized based on the target image size,
$l$, is optimized based on the target image size, ![]() $\mathit{FM}$, where
$\mathit{FM}$, where ![]() $F$ is the object size and
$F$ is the object size and ![]() $M$ is the magnification (Figure 1(c)). The distance between adjacent image centers is
$M$ is the magnification (Figure 1(c)). The distance between adjacent image centers is ![]() $l(M+1)$, which defines the maximum image size allowed for a given
$l(M+1)$, which defines the maximum image size allowed for a given ![]() $l$ and
$l$ and ![]() $M$. If the image size is larger than
$M$. If the image size is larger than ![]() $l(M+1)$, the images start to overlap, which complicates the interpretation. Thus,
$l(M+1)$, the images start to overlap, which complicates the interpretation. Thus, ![]() $l$ is determined such that
$l$ is determined such that ![]() $\mathit{FM}\lesssim l(M+1)$.
$\mathit{FM}\lesssim l(M+1)$.
Once the maximum allowed image size is defined, the appropriate tilt is determined based on the MCP strip width, ![]() $K$, so that the detector samples object spatial information most efficiently at each photon energy. In other words, the images aligned vertically across the MCP width should have a gradual horizontal shift so that, for every photon energy, they provide spatial information on a slightly different point in object space. The ideal tilt is computed by
$K$, so that the detector samples object spatial information most efficiently at each photon energy. In other words, the images aligned vertically across the MCP width should have a gradual horizontal shift so that, for every photon energy, they provide spatial information on a slightly different point in object space. The ideal tilt is computed by
as discussed in Ref. [Reference Tommasini, Koch, Izumi, Welser, Mancini, Delettrez, Regan and Smalyuk6].
An example of MMI data with an appropriate PHA tilt is shown in Figure 2(a). The object-to-pinhole distance, ![]() $p$, is
$p$, is ![]() ${\approx}3~\text{cm}$; the object-to-detector distance,
${\approx}3~\text{cm}$; the object-to-detector distance, ![]() $L$, is
$L$, is ![]() ${\approx}28.5~\text{cm}$ (
${\approx}28.5~\text{cm}$ (![]() $M\approx 8.5$). The MLM consists of 300 bilayers of W and BC, where the periodic thickness is 15 Å. Hexagonally arranged implosion core images are shown with a horizontal spectral axis. Due to K-shell line emission from Ar in the implosion core, images appearing around the photon energies associated with Ar Ly-
$M\approx 8.5$). The MLM consists of 300 bilayers of W and BC, where the periodic thickness is 15 Å. Hexagonally arranged implosion core images are shown with a horizontal spectral axis. Due to K-shell line emission from Ar in the implosion core, images appearing around the photon energies associated with Ar Ly-![]() ${\it\alpha}$ (
${\it\alpha}$ (![]() ${\sim}3320$ eV), He-
${\sim}3320$ eV), He-![]() ${\it\beta}$ (
${\it\beta}$ (![]() ${\sim}3686$ eV) and Ly-
${\sim}3686$ eV) and Ly-![]() ${\it\beta}$ (
${\it\beta}$ (![]() ${\sim}3935$ eV) are brighter. The designed tilt angle based on Equation (1) was
${\sim}3935$ eV) are brighter. The designed tilt angle based on Equation (1) was ![]() $8.95^{\circ }$ with respect to the vertical, and the data show
$8.95^{\circ }$ with respect to the vertical, and the data show ![]() $(8.66\pm 0.10)^{\circ }$. As designed, this image array efficiently provides spatial information at each photon energy. For example, Figure 2(b) shows an image reconstructed from one pixel column of the MMI data at the He-
$(8.66\pm 0.10)^{\circ }$. As designed, this image array efficiently provides spatial information at each photon energy. For example, Figure 2(b) shows an image reconstructed from one pixel column of the MMI data at the He-![]() ${\it\beta}$ line center (i.e., the orange line). Each pixel along this column is relocated into a single common image plane based on the position relative to its nearest image centers[Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9]. This single column provides strips of object spatial information that are uniformly separated over the image plane.
${\it\beta}$ line center (i.e., the orange line). Each pixel along this column is relocated into a single common image plane based on the position relative to its nearest image centers[Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9]. This single column provides strips of object spatial information that are uniformly separated over the image plane.

Figure 2. (a) MMI data with an appropriate PHA tilt. The dashed line is the reference vertical line (i.e., ![]() ${\it\theta}=0^{\circ }$). The red and green solid lines show the extracted (
${\it\theta}=0^{\circ }$). The red and green solid lines show the extracted (![]() $8.66^{\circ }$) and optimal (
$8.66^{\circ }$) and optimal (![]() $8.95^{\circ }$) PHA tilt angles. (b) Monochromatic image reconstructed from a single pixel column at the He-
$8.95^{\circ }$) PHA tilt angles. (b) Monochromatic image reconstructed from a single pixel column at the He-![]() ${\it\beta}$ line center. (c) Narrow-band He-
${\it\beta}$ line center. (c) Narrow-band He-![]() ${\it\beta}$ image reconstructed over its linewidth (i.e.,
${\it\beta}$ image reconstructed over its linewidth (i.e., ![]() ${\sim}60$ eV).
${\sim}60$ eV).
An example of MMI data with an inappropriate PHA tilt is shown in Figure 3(a). The MMI specification is identical to that of the previous example. While we used the same PHA design, it was misaligned in the MMI nose tip, which resulted in a significantly different tilt angle, ![]() $(5.22\pm 0.02)^{\circ }$, in the data. The one pixel column image provides strips that are not uniformly distributed across the image, and thus the spatial sampling is biased (Figure 3(b)).
$(5.22\pm 0.02)^{\circ }$, in the data. The one pixel column image provides strips that are not uniformly distributed across the image, and thus the spatial sampling is biased (Figure 3(b)).

Figure 3. (a) MMI data with an inappropriate PHA tilt. The dashed line is the reference vertical line (i.e., ![]() ${\it\theta}=0^{\circ }$). The red and green solid lines show the extracted (
${\it\theta}=0^{\circ }$). The red and green solid lines show the extracted (![]() $5.22^{\circ }$) and optimal (
$5.22^{\circ }$) and optimal (![]() $8.95^{\circ }$) PHA tilt angles. (b) Monochromatic image reconstructed from a single pixel column at the He-
$8.95^{\circ }$) PHA tilt angles. (b) Monochromatic image reconstructed from a single pixel column at the He-![]() ${\it\beta}$ line center. (c) Narrow-band He-
${\it\beta}$ line center. (c) Narrow-band He-![]() ${\it\beta}$ image reconstructed over its linewidth (i.e.,
${\it\beta}$ image reconstructed over its linewidth (i.e., ![]() ${\sim}60$ eV).
${\sim}60$ eV).
For both cases, one pixel column does not reconstruct the whole image, and adjacent pixel columns are needed which are at slightly different photon energies. Thus, the largest strip separation in the one pixel column image, ![]() $w$, defines the minimum width required to reconstruct the whole image, which we call the reconstruction width or sampling width. On one hand, the appropriate case shown in Figure 2 has
$w$, defines the minimum width required to reconstruct the whole image, which we call the reconstruction width or sampling width. On one hand, the appropriate case shown in Figure 2 has ![]() $w=8$ pixels. Thus, eight pixel columns are needed to fully reconstruct the image, which correspond to 15 eV for this particular dataset based on the extracted spectral axis[Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9]. Thus, the whole image can be reconstructed with a much narrower width than the spectral linewidth, where its FWHM is approximately 60 eV. By extending the narrow bandwidth to its FWHM, one can improve the signal-to-noise ratio (S/N) and form a reliable He-
$w=8$ pixels. Thus, eight pixel columns are needed to fully reconstruct the image, which correspond to 15 eV for this particular dataset based on the extracted spectral axis[Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9]. Thus, the whole image can be reconstructed with a much narrower width than the spectral linewidth, where its FWHM is approximately 60 eV. By extending the narrow bandwidth to its FWHM, one can improve the signal-to-noise ratio (S/N) and form a reliable He-![]() ${\it\beta}$ line image (Figure 2(c)). On the other hand, the inappropriate case shown in Figure 3 has
${\it\beta}$ line image (Figure 2(c)). On the other hand, the inappropriate case shown in Figure 3 has ![]() $w=20$ pixels, which corresponds to 44 eV. This is still narrower than the FWHM of the He-
$w=20$ pixels, which corresponds to 44 eV. This is still narrower than the FWHM of the He-![]() ${\it\beta}$ line. However, this means that the last pixel column added to form the whole image comes from
${\it\beta}$ line. However, this means that the last pixel column added to form the whole image comes from ![]() $44/2=22$ eV away from the line center. The overall intensity from this pixel column is systematically lower than that of the line center, and the spatial information at the center of the gap,
$44/2=22$ eV away from the line center. The overall intensity from this pixel column is systematically lower than that of the line center, and the spatial information at the center of the gap, ![]() $w$, has to rely significantly on the intensity correction discussed in Equations (3) and (4) of Ref. [Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9]. Moreover, even after reconstructing the full image, the S/N of the large gap region is still very low. Accordingly, the reconstructed image structure becomes less reliable around the large gap region.
$w$, has to rely significantly on the intensity correction discussed in Equations (3) and (4) of Ref. [Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9]. Moreover, even after reconstructing the full image, the S/N of the large gap region is still very low. Accordingly, the reconstructed image structure becomes less reliable around the large gap region.
To summarize, the PHA needs to be tilted at an appropriate angle to achieve efficient spatial sampling and minimize the reconstruction width, ![]() $w$. Reliable MMI diagnostics further require that the spectral width corresponding to
$w$. Reliable MMI diagnostics further require that the spectral width corresponding to ![]() $w$ is much narrower than the FWHM of the diagnostic lines such as He-
$w$ is much narrower than the FWHM of the diagnostic lines such as He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$. Those linewidths need to be estimated from conditions predicted with hydrodynamic simulations and taken into account to optimize the PHA design. We note that, as long as the Stark linewidth is broader than the sampling width, the diagnostics should work. However, practically speaking, a Stark width of 60 eV could still have spectral structures that change rapidly within the sampling width (e.g., structures around the center of the line). Thus, for reliable image reconstruction,
${\it\beta}$. Those linewidths need to be estimated from conditions predicted with hydrodynamic simulations and taken into account to optimize the PHA design. We note that, as long as the Stark linewidth is broader than the sampling width, the diagnostics should work. However, practically speaking, a Stark width of 60 eV could still have spectral structures that change rapidly within the sampling width (e.g., structures around the center of the line). Thus, for reliable image reconstruction, ![]() ${\rm\Delta}E_{\mathit{Stark}}>{\rm\Delta}E_{\mathit{instrum}}>w$ is ideal, where
${\rm\Delta}E_{\mathit{Stark}}>{\rm\Delta}E_{\mathit{instrum}}>w$ is ideal, where ![]() ${\rm\Delta}E_{\mathit{Stark}}$ and
${\rm\Delta}E_{\mathit{Stark}}$ and ![]() ${\rm\Delta}E_{\mathit{instrum}}$ are the Stark width of the line and the spectral resolution of the instrument, respectively.
${\rm\Delta}E_{\mathit{instrum}}$ are the Stark width of the line and the spectral resolution of the instrument, respectively.
The extracted one pixel column image such as Figures 2(b) and 3(b) gives some idea of how reliable the recorded MMI data are. However, it does not directly answer how critical it is to satisfy this criterion. To better illustrate this point, we perform a synthetic investigation in Section 4 using the spectral model discussed in Section 3.
3. Spectral model
The spectral model used in this paper computes emergent spectra at every point on the image plane, ![]() $I_{{\it\nu}}(x,y)$, and then
$I_{{\it\nu}}(x,y)$, and then ![]() $I_{{\it\nu}}(x,y)$ is used to compute both synthetic MMI data and expected images. The case of investigation is an OMEGA direct-drive Ar-doped
$I_{{\it\nu}}(x,y)$ is used to compute both synthetic MMI data and expected images. The case of investigation is an OMEGA direct-drive Ar-doped ![]() $\text{D}_{2}$-filled ICF implosion because it has been one of our main applications of the MMI diagnostics[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10–Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12]. The ICF implosion core is the object for the synthetic data, and we define it as a sphere of uniform
$\text{D}_{2}$-filled ICF implosion because it has been one of our main applications of the MMI diagnostics[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk10–Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12]. The ICF implosion core is the object for the synthetic data, and we define it as a sphere of uniform ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ to simplify the interpretation of the synthetic investigation. The capsule is initially filled with 20 atm of
$n_{e}$ to simplify the interpretation of the synthetic investigation. The capsule is initially filled with 20 atm of ![]() $\text{D}_{2}$ with 0.18% atomic concentration of Ar. The Ar photon-energy-dependent emissivity and opacity are computed for given
$\text{D}_{2}$ with 0.18% atomic concentration of Ar. The Ar photon-energy-dependent emissivity and opacity are computed for given ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$, and emergent spectra are computed by solving the radiation transport along each chord parallel to the line of sight[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12].
$n_{e}$, and emergent spectra are computed by solving the radiation transport along each chord parallel to the line of sight[Reference Nagayama, Mancini, Florido, Mayes, Tommasini, Koch, Delettrez, Regan and Smalyuk12].
To compute the Ar emissivity, ![]() ${\it\epsilon}_{{\it\nu}}$, and opacity,
${\it\epsilon}_{{\it\nu}}$, and opacity, ![]() ${\it\kappa}_{{\it\nu}}$, necessary atomic data are computed with the Flexible Atomic Code (FAC)[Reference Gu14], and Ar level populations are solved for the given
${\it\kappa}_{{\it\nu}}$, necessary atomic data are computed with the Flexible Atomic Code (FAC)[Reference Gu14], and Ar level populations are solved for the given ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ with a collisional–radiative model, ABAKO[Reference Florido, Rodríguez, Gil, Rubiano, Martel, Mínguez and Mancini15]. We used the Stewart and Pyatt model[Reference Stewart and Pyatt16] for continuum lowering effects and the escape factor approximation to account for radiation transport effects on the populations[Reference Mancini, Joyce and Hooper17]. The spectral emissivity and opacity are computed from the calculated populations including detailed Stark line profiles computed by MERL[Reference Mancini, Kilcrease, Woltz and Hooper18].
$n_{e}$ with a collisional–radiative model, ABAKO[Reference Florido, Rodríguez, Gil, Rubiano, Martel, Mínguez and Mancini15]. We used the Stewart and Pyatt model[Reference Stewart and Pyatt16] for continuum lowering effects and the escape factor approximation to account for radiation transport effects on the populations[Reference Mancini, Joyce and Hooper17]. The spectral emissivity and opacity are computed from the calculated populations including detailed Stark line profiles computed by MERL[Reference Mancini, Kilcrease, Woltz and Hooper18].
Emergent spectra are computed along each chord on the image plane by numerically integrating the radiation transport equation assuming parallel ray tracing[Reference Mihalas19]:
where the ![]() $z$ axis is parallel to the line of sight, the
$z$ axis is parallel to the line of sight, the ![]() $x{-}y$ plane is parallel to the image plane of the detector,
$x{-}y$ plane is parallel to the image plane of the detector, ![]() $I_{{\it\nu}}(x,y)$ is the emergent intensity at
$I_{{\it\nu}}(x,y)$ is the emergent intensity at ![]() $(x,y)$ on the source (
$(x,y)$ on the source (![]() $\text{erg}/\text{s}/\text{cm}^{2}/\text{sr}/\text{eV}$) and
$\text{erg}/\text{s}/\text{cm}^{2}/\text{sr}/\text{eV}$) and ![]() ${\it\tau}_{{\it\nu}}$ is the optical depth from point
${\it\tau}_{{\it\nu}}$ is the optical depth from point ![]() $z$ in the object to the observer side of the object surface. The quantities
$z$ in the object to the observer side of the object surface. The quantities ![]() ${\it\epsilon}_{{\it\nu}}(x,y,z)$ and
${\it\epsilon}_{{\it\nu}}(x,y,z)$ and ![]() ${\it\kappa}_{{\it\nu}}(x,y,z)$ are determined with ABAKO at the given
${\it\kappa}_{{\it\nu}}(x,y,z)$ are determined with ABAKO at the given ![]() $T_{e}$ and
$T_{e}$ and ![]() $n_{e}$ if
$n_{e}$ if ![]() $(x,y,z)$ is inside the object and zero if it is outside the object.
$(x,y,z)$ is inside the object and zero if it is outside the object.
Potential inaccuracy in the calculated emissivity and opacity does not affect the conclusions derived from the synthetic investigations performed in this paper because ![]() $I_{{\it\nu}}(x,y)$ is used to calculate both the synthetic MMI data and the expected images. What we pursue is the discrepancies produced due to the discrete nature of MMI data and the details of data processing.
$I_{{\it\nu}}(x,y)$ is used to calculate both the synthetic MMI data and the expected images. What we pursue is the discrepancies produced due to the discrete nature of MMI data and the details of data processing.
The expected narrow-band images are computed by integrating ![]() $I_{{\it\nu}}(x,y)$ over any given spectral range as
$I_{{\it\nu}}(x,y)$ over any given spectral range as
where ![]() ${\rm\Delta}{\it\nu}$ is the bandwidth of interest.
${\rm\Delta}{\it\nu}$ is the bandwidth of interest.
Synthetic MMI data are computed from the emergent spectra, ![]() $I_{{\it\nu}}(x,y)$, assuming parallel ray tracing. When MMI data are processed as discussed in Ref. [Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9], each MMI pixel,
$I_{{\it\nu}}(x,y)$, assuming parallel ray tracing. When MMI data are processed as discussed in Ref. [Reference Nagayama, Mancini, Florido, Tommasini, Koch, Delettrez, Regan and Smalyuk9], each MMI pixel, ![]() $(x_{mmi},y_{mmi})$, uniquely defines its photon energy,
$(x_{mmi},y_{mmi})$, uniquely defines its photon energy, ![]() $h{\it\nu}$, and its position on the image plane,
$h{\it\nu}$, and its position on the image plane, ![]() $(x,y)$. Thus, using this pixel information provided from actual MMI data, one can compute each pixel of synthetic MMI data as
$(x,y)$. Thus, using this pixel information provided from actual MMI data, one can compute each pixel of synthetic MMI data as ![]() $I_{{\it\nu}}(x,y){\rm\Delta}h{\it\nu}{\rm\Delta}A$ by converting every pixel
$I_{{\it\nu}}(x,y){\rm\Delta}h{\it\nu}{\rm\Delta}A$ by converting every pixel ![]() $(x_{mmi},y_{mmi})$ into
$(x_{mmi},y_{mmi})$ into ![]() $(x,y)$ and
$(x,y)$ and ![]() $h{\it\nu}$. Here,
$h{\it\nu}$. Here, ![]() ${\rm\Delta}h{\it\nu}$ and
${\rm\Delta}h{\it\nu}$ and ![]() ${\rm\Delta}A$ are the finite spectral width and the finite area at the pixel
${\rm\Delta}A$ are the finite spectral width and the finite area at the pixel ![]() $(x_{mmi},y_{mmi})$.
$(x_{mmi},y_{mmi})$.
One concern is the validity of parallel ray tracing for the synthetic MMI data modeling. While photons going through pinholes are not precisely parallel, the parallel ray assumption is still valid for our applications. Based on the object size of ![]() $100~{\rm\mu}\text{m}$ and object–PHA distance of 3 cm, rays through a single pinhole deviate from parallel by less than
$100~{\rm\mu}\text{m}$ and object–PHA distance of 3 cm, rays through a single pinhole deviate from parallel by less than ![]() ${\it\theta}<\arctan \;(100~{\rm\mu}\text{m}/3~\text{cm})=0.2^{\circ }$. This maximum deviation in angle can be interpreted in terms of the maximum deviation on the image plane as
${\it\theta}<\arctan \;(100~{\rm\mu}\text{m}/3~\text{cm})=0.2^{\circ }$. This maximum deviation in angle can be interpreted in terms of the maximum deviation on the image plane as ![]() $(100~{\rm\mu}\text{m})\times \sin (0.2^{\circ })<0.3~{\rm\mu}\text{m}$, which is much smaller than the typical spatial resolution of the image,
$(100~{\rm\mu}\text{m})\times \sin (0.2^{\circ })<0.3~{\rm\mu}\text{m}$, which is much smaller than the typical spatial resolution of the image, ![]() ${\rm\Delta}x\approx 11~{\rm\mu}\text{m}$.
${\rm\Delta}x\approx 11~{\rm\mu}\text{m}$.
Photons through different pinholes have a larger deviation from the parallel rays. In typical data, pinholes used to project images on a single MCP are separated by a maximum of ![]() ${\sim}2~\text{mm}$. Then, photons going through those pinholes could deviate from parallel by up to
${\sim}2~\text{mm}$. Then, photons going through those pinholes could deviate from parallel by up to ![]() ${\it\theta}<\arctan \;(2~\text{mm}/3~\text{cm})=3.8^{\circ }$. Along the maximum chord length in the object, this results in a chord deviation of
${\it\theta}<\arctan \;(2~\text{mm}/3~\text{cm})=3.8^{\circ }$. Along the maximum chord length in the object, this results in a chord deviation of ![]() $(100~{\rm\mu}\text{m})\times \sin (3.8^{\circ })=6.6~{\rm\mu}\text{m}$ on the image plane. This deviation is still less than the spatial resolution of the instrument. Furthermore, this deviation is an upper bound because usually only a smaller portion of the MMI data is used in the analysis. For example, for He-
$(100~{\rm\mu}\text{m})\times \sin (3.8^{\circ })=6.6~{\rm\mu}\text{m}$ on the image plane. This deviation is still less than the spatial resolution of the instrument. Furthermore, this deviation is an upper bound because usually only a smaller portion of the MMI data is used in the analysis. For example, for He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ analysis, the most distant pinholes used in the analysis are separated by less than 1 mm, and thus the deviation on the image plane is less than
${\it\beta}$ analysis, the most distant pinholes used in the analysis are separated by less than 1 mm, and thus the deviation on the image plane is less than ![]() $3.3~{\rm\mu}\text{m}$. Hence, parallel ray tracing is a good approximation to interpret the photon paths through the object for many MMI applications, including ours.
$3.3~{\rm\mu}\text{m}$. Hence, parallel ray tracing is a good approximation to interpret the photon paths through the object for many MMI applications, including ours.
4. Impact of the criterion on MMI spatial sampling
The quality of the MMI data depends on whether or not ![]() $w$ is significantly narrower than the spectral linewidth. In this section, we synthetically investigate the impact of the criterion on the reliability of the extracted spatial information. This can be demonstrated by reconstructing images from the synthetic MMI data that do and do not satisfy the criterion and comparing them with the expected images.
$w$ is significantly narrower than the spectral linewidth. In this section, we synthetically investigate the impact of the criterion on the reliability of the extracted spatial information. This can be demonstrated by reconstructing images from the synthetic MMI data that do and do not satisfy the criterion and comparing them with the expected images.
First, MMI data with an appropriate PHA are created using a uniform sphere of ![]() $100~{\rm\mu}\text{m}$ diameter,
$100~{\rm\mu}\text{m}$ diameter, ![]() $T_{e}=1500$ and
$T_{e}=1500$ and ![]() $n_{e}=1.5\times 10^{24}~\text{cm}^{-3}$. The PHA pattern and the photon-energy axis are those from the appropriate data shown in Figure 2(a). The conditions are the values representative of Figure 2(a) based on the analysis of its space-integrated spectra. Thus, as already discussed in Section 2,
$n_{e}=1.5\times 10^{24}~\text{cm}^{-3}$. The PHA pattern and the photon-energy axis are those from the appropriate data shown in Figure 2(a). The conditions are the values representative of Figure 2(a) based on the analysis of its space-integrated spectra. Thus, as already discussed in Section 2, ![]() $w=$ 8 pixels (i.e.,
$w=$ 8 pixels (i.e., ![]() ${\sim}15$ eV) and the FWHMs of the He-
${\sim}15$ eV) and the FWHMs of the He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ lines are roughly 60 eV, which satisfies
${\it\beta}$ lines are roughly 60 eV, which satisfies ![]() $w\ll$ FWHM.
$w\ll$ FWHM.
Figure 4(a) shows the resultant synthetic MMI data. Because ![]() $w$ is much narrower than the FWHMs of the spectral lines, the reconstructed He-
$w$ is much narrower than the FWHMs of the spectral lines, the reconstructed He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ images shown in Figure 4(b) agree very well with the expected images shown in Figure 4(c).
${\it\beta}$ images shown in Figure 4(b) agree very well with the expected images shown in Figure 4(c).

Figure 4. (a) Synthetic MMI data with an appropriate PHA tilt and with the minimum reconstruction width, ![]() $w$, much narrower than the spectral linewidth. (b) Ar He-
$w$, much narrower than the spectral linewidth. (b) Ar He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ images reconstructed from the synthetic MMI data. (c) Expected Ar He-
${\it\beta}$ images reconstructed from the synthetic MMI data. (c) Expected Ar He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ images.
${\it\beta}$ images.
We note that there are small vertical structures introduced in the Ly-![]() ${\it\beta}$ image in Figure 4(b). These structures come from the discrete nature of the MMI data. The MMI data have only a finite number of images, each of which spans slightly different photon-energy ranges. The processing tool combines the finite information from the different pinhole images together to approximate narrow-band images, and small discrepancies are unavoidable. The level of discrepancies can be quantified by series of synthetic investigations, which are beyond the scope of the paper and will be discussed elsewhere.
${\it\beta}$ image in Figure 4(b). These structures come from the discrete nature of the MMI data. The MMI data have only a finite number of images, each of which spans slightly different photon-energy ranges. The processing tool combines the finite information from the different pinhole images together to approximate narrow-band images, and small discrepancies are unavoidable. The level of discrepancies can be quantified by series of synthetic investigations, which are beyond the scope of the paper and will be discussed elsewhere.
Next, inappropriate MMI data are synthetically created using a uniform sphere of ![]() $100~{\rm\mu}\text{m}$ diameter,
$100~{\rm\mu}\text{m}$ diameter, ![]() $T_{e}=1000~\text{eV}$ and
$T_{e}=1000~\text{eV}$ and ![]() $n_{e}=3\times 10^{23}~\text{cm}^{-3}$. The PHA pattern and the photon-energy axis are those from the actual inappropriate MMI data shown in Figure 3(a). Thus, the minimum width required to reconstruct the image is
$n_{e}=3\times 10^{23}~\text{cm}^{-3}$. The PHA pattern and the photon-energy axis are those from the actual inappropriate MMI data shown in Figure 3(a). Thus, the minimum width required to reconstruct the image is ![]() $w=20$ pixels (i.e., 44 eV), as discussed in Section 2. One reason why Figure 3(c) still shows a reasonable image is that
$w=20$ pixels (i.e., 44 eV), as discussed in Section 2. One reason why Figure 3(c) still shows a reasonable image is that ![]() $w$ is still narrower than the linewidth (
$w$ is still narrower than the linewidth (![]() ${\sim}60$ eV), while it is not significantly narrower. Thus, to show an extreme case,
${\sim}60$ eV), while it is not significantly narrower. Thus, to show an extreme case, ![]() $n_{e}$ is purposely lowered so that
$n_{e}$ is purposely lowered so that ![]() $w$ becomes even broader than its Stark linewidth (
$w$ becomes even broader than its Stark linewidth (![]() ${\sim}16{-}19$ eV).
${\sim}16{-}19$ eV).
Figure 5(a) displays the resultant synthetic MMI data, which show much narrower spectral features compared with Figure 3(a). Figure 5(b) shows the reconstructed Ar He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ images. Compared with the expected images (Figure 5(c)), the reconstructed images have a lot of artificial structure originating from the discrete nature of the MMI data, which is amplified due to
${\it\beta}$ images. Compared with the expected images (Figure 5(c)), the reconstructed images have a lot of artificial structure originating from the discrete nature of the MMI data, which is amplified due to ![]() $w>$ FWHM.
$w>$ FWHM.

Figure 5. (a) Synthetic MMI data with an inappropriate PHA tilt and with the minimum reconstruction width, ![]() $w$, broader than the spectral linewidth. (b) Ar He-
$w$, broader than the spectral linewidth. (b) Ar He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ images reconstructed from the synthetic MMI data. (c) Expected Ar He-
${\it\beta}$ images reconstructed from the synthetic MMI data. (c) Expected Ar He-![]() ${\it\beta}$ and Ly-
${\it\beta}$ and Ly-![]() ${\it\beta}$ images.
${\it\beta}$ images.
5. Conclusions
The MMI instrument is an interesting diagnostic tool to study the spatial structure of ICF plasmas. This paper discusses the criterion for reliable MMI diagnostics and its impact on the extracted spatial information. Reliable MMI data have a sampling width, ![]() $w$, much narrower than the FWHM of the spectral lines. An appropriate PHA tilt is critical to minimize
$w$, much narrower than the FWHM of the spectral lines. An appropriate PHA tilt is critical to minimize ![]() $w$ for a given target image size and MCP strip width.
$w$ for a given target image size and MCP strip width.
By processing synthetically generated MMI data, we demonstrated that MMI data with ![]() $w>$ FWHM produce significant bias in the sampled object spatial information. On one hand, the images reconstructed from appropriate MMI data are very similar to those of the expected images. On the other hand, the images from inappropriate MMI data show very different spatial structures from the expected ones. The artificial structure is always vertical due to the fact that the images are reconstructed by superposition of vertical strips originating from different pixel columns. The presence of strong vertical structure in the image is probably a sign that the MMI data are flawed, and is most likely due to not satisfying the criterion. Reliability in the conclusions derived from such inappropriate MMI data is limited.
$w>$ FWHM produce significant bias in the sampled object spatial information. On one hand, the images reconstructed from appropriate MMI data are very similar to those of the expected images. On the other hand, the images from inappropriate MMI data show very different spatial structures from the expected ones. The artificial structure is always vertical due to the fact that the images are reconstructed by superposition of vertical strips originating from different pixel columns. The presence of strong vertical structure in the image is probably a sign that the MMI data are flawed, and is most likely due to not satisfying the criterion. Reliability in the conclusions derived from such inappropriate MMI data is limited.
Acknowledgements
This work was supported by DOE/NLUF grant nos. DE-NA0000859 and DE-NA0002267, and LLNL.