Research Article
Quotients of F-spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-108
-
- Article
-
- You have access
- Export citation
Idempotents in completely 0-simple semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 109-113
-
- Article
-
- You have access
- Export citation
Circles of numbers
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-119
-
- Article
-
- You have access
- Export citation
Category of sequences of zeros and ones in some FK spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-124
-
- Article
-
- You have access
- Export citation
On images and inverse images of Weierstrass points†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 125-128
-
- Article
-
- You have access
- Export citation
Ranges of Lyapunov Transformations for operator algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 129-134
-
- Article
-
- You have access
- Export citation
Groups of complexes of a representable lattice-ordered group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 135-139
-
- Article
-
- You have access
- Export citation
Groups of breadth four have class five
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 141-148
-
- Article
-
- You have access
- Export citation
Projective representations of extra-special p-groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 149-152
-
- Article
-
- You have access
- Export citation
Lower central depth in finitely generated soluble-by-finite groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-154
-
- Article
-
- You have access
- Export citation
Whitehead groups of semidirect products of free groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 155-158
-
- Article
-
- You have access
- Export citation
On groups with decomposable commutator subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-162
-
- Article
-
- You have access
- Export citation
An acyclic analogue to Heawood's theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 163-166
-
- Article
-
- You have access
- Export citation
Unique factorization in rings with right ACC1
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 167-171
-
- Article
-
- You have access
- Export citation
On the representation of a number as a sum of squares
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-197
-
- Article
-
- You have access
- Export citation
π-domains, overrings, and divisorial ideals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-203
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 18 May 2009, p. 205
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 19 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 19 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, p. b1
-
- Article
-
- You have access
- Export citation

 and
and
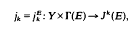
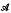 be a C
be a C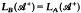
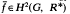 represented by the central factor system
represented by the central factor system 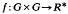 we associate the so called twisted group algebra (
we associate the so called twisted group algebra (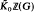 . Let α be an automorphism of
. Let α be an automorphism of 



 is a cusp form (as was first pointed out by Mordell [
is a cusp form (as was first pointed out by Mordell [ then are replaced by modular forms for a subgroup of the Hilbert modular group with Fourier expansions of the form (10) (see section 2).
then are replaced by modular forms for a subgroup of the Hilbert modular group with Fourier expansions of the form (10) (see section 2).