Research Article
Algebras stably equivalent to selfinjective algebras whose Auslander-Reiten quivers consist only of generalized standard components
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-19
-
- Article
-
- You have access
- Export citation
Multiplicity of Boardman strata and deformations of map germs
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-32
-
- Article
-
- You have access
- Export citation
Dehn functions and complexes of groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 33-46
-
- Article
-
- You have access
- Export citation
Almost-Bieberbach groups with (in)finite outer automorphism group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 47-62
-
- Article
-
- You have access
- Export citation
On 2-class field towers for quadratic number fields with 2-class group of type (2,2)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-69
-
- Article
-
- You have access
- Export citation
Hilbert cusp forms and special values of Dirichlet series of Rankin type
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 71-77
-
- Article
-
- You have access
- Export citation
Gauss sums for U(2n, q2)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 79-95
-
- Article
-
- You have access
- Export citation
Bounded mean curvature isometric immersions of a compact Riemannian manifold with images contained in a tube
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-107
-
- Article
-
- You have access
- Export citation
Totally real pseudo-umbilical submanifolds of a quaternion space form
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 109-115
-
- Article
-
- You have access
- Export citation
Commutator length of abelian-by-nilpotent groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 117-121
-
- Article
-
- You have access
- Export citation
On the spectrum of n-tuples of p-hyponormal operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-131
-
- Article
-
- You have access
- Export citation
Existence de sous-espaces hyper-invariants
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 133-141
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 40 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 40 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

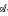 -invariant. If
-invariant. If  of
of  of ideles of
of ideles of  denote the space of Hilbert cusp forms of holomorphic type on ℋ
denote the space of Hilbert cusp forms of holomorphic type on ℋ , where 1 is the trivial character. If
, where 1 is the trivial character. If  sending
sending  be the adjoint of the linear map Φ
be the adjoint of the linear map Φ
