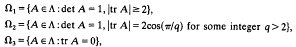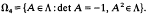Research Article
On an integral transform
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-14
-
- Article
-
- You have access
- Export citation
On Pontryagin duality
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 15-24
-
- Article
-
- You have access
- Export citation
Semigroups of continuous selfmaps for which Green's
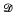 and ℐ relations coincide
and ℐ relations coincide
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 25-28
-
- Article
-
- You have access
- Export citation
Finite quasi-injective groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 29-33
-
- Article
-
- You have access
- Export citation
An application of some fractional integrals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 35-41
-
- Article
-
- You have access
- Export citation
On the Occurrence of large gaps between prime numbers
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 43-48
-
- Article
-
- You have access
- Export citation
Triple orthogonal series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-53
-
- Article
-
- You have access
- Export citation
The twisted group algebra of a finite nilpotent group over a number field
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-61
-
- Article
-
- You have access
- Export citation
Remarks on the commutativity of the radicals of group algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-68
-
- Article
-
- You have access
- Export citation
Discrete free products of two complex cyclic matrix groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 69-80
-
- Article
-
- You have access
- Export citation
Endomorphism monoids of distributive double p-algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 81-86
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 20 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 20 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, p. b1
-
- Article
-
- You have access
- Export citation

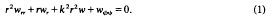
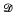 and ℐ relations coincide
and ℐ relations coincide
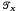 the full transformation semigroup on the set
the full transformation semigroup on the set