Research Article
On entire functions with gap power series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 89-97
-
- Article
-
- You have access
- Export citation
On smallest radical and semi-simple classes
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 98-104
-
- Article
-
- You have access
- Export citation
Bounded generators in linear topological spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 105-109
-
- Article
-
- You have access
- Export citation
Some convexity theorems for matrices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 110-117
-
- Article
-
- You have access
- Export citation
Homology and the Koszul complex
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 118-135
-
- Article
-
- You have access
- Export citation
Hook representations of the symmetric groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 136-149
-
- Article
-
- You have access
- Export citation
Generalized semigroups of quotients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 150-161
-
- Article
-
- You have access
- Export citation
On the flat overrings of an integral domain
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 162-165
-
- Article
-
- You have access
- Export citation
Abstract integral spaces and minimal extensions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 166-178
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 12 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 12 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



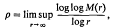
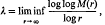
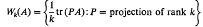
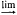 Hom
Hom