Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Suslin, A. A.
1985.
Algebraic K-theory.
Journal of Soviet Mathematics,
Vol. 28,
Issue. 6,
p.
870.


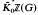 . For undefined terminologies used in the paper, we refer to [3] and [6].
. For undefined terminologies used in the paper, we refer to [3] and [6].