Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-30T15:25:13.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological invariants of germs of real analytic functions

Published online by Cambridge University Press:  18 May 2009

Piotr Dudziński
Piotr Dudziński
Affiliation:
Institute of Mathematics, University of Gdańsk, 80-925 Gdańsk, Wita Stwosza 57, Polande-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f: (ℝn, 0)→ (ℝ,0) be a germ of a real analytic function. Let L and F(f) denote the link of f and the Milnor fibre of fc respectively, i. e., L = {x ∈ Sn−1 | f(x) = 0}, 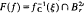, where 0 ≤ ξ ≪ r ≪ 1, 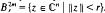. In [2] Szafraniec introduced the notion of an 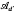-germ as a generalization of a germ defined by a weighted homogeneous polynomial satisfying some condition concerning the relation between its degree and weights (definition 1). He also proved that if f is an 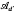-germ (presumably with nonisolated singularity) then the number χ(F(f)/d mod 2 is a topological invariant of f, where χ(F(f)) is the Euler characterististic of F(f), and gave the formula for χ(L)/2 mod 2 (it is a well-known fact that F(L) is an even number). As a simple consequence he got the fact that χ(F(f)mod 2 is a topological invariant for any f, which is a generalization of Wall's result [3] (he considered only germs with an isolated singularity).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 1 , January 1997 , pp. 85 - 89
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Milnor, J., Singular points of complex hypersurfaces (Princeton University Press 1968).Google Scholar
2.Szafraniec, Z., On the topological invariants of germs of analytic functions Topology 26 (1987), 235–238.Google Scholar
3.Wall, C. T. C., Topological invariance of the Milnor number mod 2, Topology 22 (1983), 345–350.Google Scholar