No CrossRef data available.
Article contents
Toeplitz operators and algebras of bounded analytic functions on the disk
Published online by Cambridge University Press: 18 May 2009
Extract
Here and throughout, A is a closed subalgebra of H∞ that contains the disk algebra and M(A) denotes the maximal ideal space of A. Because A contains the function fo(z) = z, we can define the fiber Mλ(A) of M(A) for λ ε ∂D (the unit circle) in the usual way; i.e., Mλ(A) = {φ ∈ M(A): fo(φ) = λ}. The Bergman space  of the unit disk D is the L2(D, dx dy)-closure of A. Let
of the unit disk D is the L2(D, dx dy)-closure of A. Let 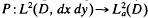 be the orthogonal projection. For f ∈ L∞(D, dx dy), define the multiplication operator Mf: L2(D, dx dy)→ L2, (D, dx dy) by
be the orthogonal projection. For f ∈ L∞(D, dx dy), define the multiplication operator Mf: L2(D, dx dy)→ L2, (D, dx dy) by
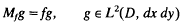
and define the Toeplitz operator 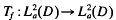 by
by
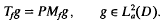
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1991


