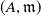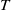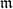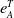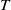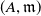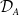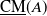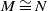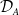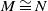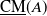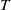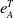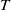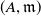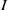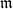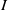1. Introduction
For ease of reference, it is advisable to have a copy of [Reference Puthenpurakal20] on hand while reading this paper. The notations employed here are consistent with those used in [Reference Puthenpurakal20].
Let
![]() $(A,{\mathfrak{m}})$
be a Cohen–Macaulay local ring of dimension
$(A,{\mathfrak{m}})$
be a Cohen–Macaulay local ring of dimension
![]() $d \geq 1$
and let
$d \geq 1$
and let
![]() ${\mathrm{CM}}(A)$
be the category of maximal Cohen–Macaulay
${\mathrm{CM}}(A)$
be the category of maximal Cohen–Macaulay
![]() $A$
-modules. In [Reference Puthenpurakal20], the second author has constructed
$A$
-modules. In [Reference Puthenpurakal20], the second author has constructed
![]() $T \colon{\mathrm{CM}}(A)\times{\mathrm{CM}}(A) \rightarrow \mathrm{mod}(A)$
, a sub-functor of
$T \colon{\mathrm{CM}}(A)\times{\mathrm{CM}}(A) \rightarrow \mathrm{mod}(A)$
, a sub-functor of
![]() $\mathrm{Ext}^1_A(-, -)$
as follows: Let
$\mathrm{Ext}^1_A(-, -)$
as follows: Let
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module. Set
$A$
-module. Set
This function arose in the second author’s study of certain aspects of the theory of Hilbert functions [Reference Puthenpurakal15, Reference Puthenpurakal16]. Using [Reference Puthenpurakal15, Theorem 18], we get that
![]() $e^T_A(M)$
is a finite number, and it is zero if and only if
$e^T_A(M)$
is a finite number, and it is zero if and only if
![]() $M$
is free. Let
$M$
is free. Let
![]() $s \colon 0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$
be an exact sequence of MCM
$s \colon 0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$
be an exact sequence of MCM
![]() $A$
-modules. Then by [Reference Puthenpurakal17, 2.6], we get that
$A$
-modules. Then by [Reference Puthenpurakal17, 2.6], we get that
![]() $e^T_A(E) \leq e^T_A(M) + e^T_A(N)$
. Set
$e^T_A(E) \leq e^T_A(M) + e^T_A(N)$
. Set
![]() $e^T(s) = e^T_A(M) + e^T_A(N) - e^T_A(E)$
.
$e^T(s) = e^T_A(M) + e^T_A(N) - e^T_A(E)$
.
Definition 1.1. We say
![]() $s$
is
$s$
is
![]() $T$
-
split if
$T$
-
split if
![]() $e^T_A(s) = 0$
.
$e^T_A(s) = 0$
.
Definition 1.2. Let
![]() $M, N$
be MCM
$M, N$
be MCM
![]() $A$
-modules. Set
$A$
-modules. Set
We proved [Reference Puthenpurakal20, 1.4],
Theorem 1.3.
(with notation as above)
![]() $T_A \colon{\mathrm{CM}}(A)\times{\mathrm{CM}}(A) \rightarrow \mathrm{mod}(A)$
is a sub-functor of
$T_A \colon{\mathrm{CM}}(A)\times{\mathrm{CM}}(A) \rightarrow \mathrm{mod}(A)$
is a sub-functor of
![]() $\mathrm{Ext}^1_A(-, -)$
.
$\mathrm{Ext}^1_A(-, -)$
.
Note that the most natural context for the sub-functors of
![]() $\mathrm{Ext}$
is exact categories (e.g., see [Reference Dräxler, Reiten, Smalø and Solberg9, Section 1], [Reference Bühler6]).
$\mathrm{Ext}$
is exact categories (e.g., see [Reference Dräxler, Reiten, Smalø and Solberg9, Section 1], [Reference Bühler6]).
It is not clear from the definition whether
![]() $T_A(M,N)$
is nonzero. Theorem [Reference Puthenpurakal20, 1.5] shows that there are plenty of
$T_A(M,N)$
is nonzero. Theorem [Reference Puthenpurakal20, 1.5] shows that there are plenty of
![]() $T$
-split extensions if
$T$
-split extensions if
![]() $\dim \mathrm{Ext}^1_A(M,N) \gt 0$
. We proved [Reference Puthenpurakal20, 1.5]
$\dim \mathrm{Ext}^1_A(M,N) \gt 0$
. We proved [Reference Puthenpurakal20, 1.5]
Theorem 1.4.
Let
![]() $(A,{\mathfrak{m}})$
be a Cohen–Macaulay local ring and let
$(A,{\mathfrak{m}})$
be a Cohen–Macaulay local ring and let
![]() $M,N$
be MCM
$M,N$
be MCM
![]() $A$
-modules. Then
$A$
-modules. Then
Note Theorem1.4 has no content if
![]() $M$
is free on the punctured spectrum of
$M$
is free on the punctured spectrum of
![]() $A$
. One of our motivations of this paper was to investigate
$A$
. One of our motivations of this paper was to investigate
![]() $T_A(M, N)$
when
$T_A(M, N)$
when
![]() $M$
is free on the punctured spectrum of
$M$
is free on the punctured spectrum of
![]() $A$
.
$A$
.
Now assume
![]() $(A,{\mathfrak{m}})$
is Henselian and
$(A,{\mathfrak{m}})$
is Henselian and
![]() $M$
is an indecomposable MCM
$M$
is an indecomposable MCM
![]() $A$
-module with
$A$
-module with
![]() $M_{\mathfrak{p}}$
is free for all
$M_{\mathfrak{p}}$
is free for all
![]() $\mathfrak{p}\in$
Spec
$\mathfrak{p}\in$
Spec
![]() $^0(A)=$
Spec
$^0(A)=$
Spec
![]() $(A)\setminus \{\mathfrak{m}\}$
, then a fundamental short exact sequence is known as the Auslander–Reiten (AR)-sequence ending at
$(A)\setminus \{\mathfrak{m}\}$
, then a fundamental short exact sequence is known as the Auslander–Reiten (AR)-sequence ending at
![]() $M$
exists. For a good introduction to AR-sequences, see [Reference Yoshino23, Chapter 2].
$M$
exists. For a good introduction to AR-sequences, see [Reference Yoshino23, Chapter 2].
The following result gives a large number of examples of AR-sequences which are
![]() $T$
-split.
$T$
-split.
Theorem 1.5.
Let
![]() $(Q,\mathfrak{n})$
be a Henselian regular local ring and
$(Q,\mathfrak{n})$
be a Henselian regular local ring and
![]() $\underline{f} = f_1,\ldots, f_c\in \mathfrak{n}^2$
a regular sequence. Set
$\underline{f} = f_1,\ldots, f_c\in \mathfrak{n}^2$
a regular sequence. Set
![]() $I=(f_1,\ldots, f_c)$
and
$I=(f_1,\ldots, f_c)$
and
![]() $(A,\mathfrak{m})= (Q/I,\mathfrak{n}/I)$
. Assume
$(A,\mathfrak{m})= (Q/I,\mathfrak{n}/I)$
. Assume
![]() $\dim A = 1$
. Let
$\dim A = 1$
. Let
![]() $M$
be an indecomposable MCM
$M$
be an indecomposable MCM
![]() $A$
-module with
$A$
-module with
![]() $\mathrm{cx}_A M\geq 2$
. Assume
$\mathrm{cx}_A M\geq 2$
. Assume
![]() $M$
is free on Spec
$M$
is free on Spec
![]() $^0(A)$
. Set
$^0(A)$
. Set
![]() $M_n= \mathrm{Syz}_n^A(M)$
, then for
$M_n= \mathrm{Syz}_n^A(M)$
, then for
![]() $n\gg 0$
the AR-sequences ending in
$n\gg 0$
the AR-sequences ending in
![]() $M_n$
are
$M_n$
are
![]() $T$
-split.
$T$
-split.
For hypersurfaces defined by quadrics, we prove:
Theorem 1.6.
Let
![]() $(Q,\mathfrak{n})$
be a Henselian regular local ring with algebraically closed residue field
$(Q,\mathfrak{n})$
be a Henselian regular local ring with algebraically closed residue field
![]() $k = Q/\mathfrak{n}$
and let
$k = Q/\mathfrak{n}$
and let
![]() $f \in \mathfrak{n}^2 \setminus \mathfrak{n}^3$
. Assume the hypersurface
$f \in \mathfrak{n}^2 \setminus \mathfrak{n}^3$
. Assume the hypersurface
![]() $A = Q/(f)$
is an isolated singularity. Then all but finitely many AR-sequences in
$A = Q/(f)$
is an isolated singularity. Then all but finitely many AR-sequences in
![]() $A$
are
$A$
are
![]() $T$
-split.
$T$
-split.
Theorems1.5 and 1.6 show that
![]() $T$
-split sequences are abundant in general. However, the following example is important:
$T$
-split sequences are abundant in general. However, the following example is important:
Example 1.7.
There exists a complete hypersurface isolated singularity
![]() $A$
and an indecomposable MCM
$A$
and an indecomposable MCM
![]() $A$
-module
$A$
-module
![]() $M$
such that
$M$
such that
![]() $T_A(M, N) = 0$
for any MCM
$T_A(M, N) = 0$
for any MCM
![]() $A$
-module
$A$
-module
![]() $N$
.
$N$
.
Theorem 1.8.
Now assume
![]() $A$
is Gorenstein. As observed in [Reference Puthenpurakal17], the function
$A$
is Gorenstein. As observed in [Reference Puthenpurakal17], the function
![]() $e^T_A(-)$
is in fact a function on
$e^T_A(-)$
is in fact a function on
![]() $\underline{\mathrm{CM}}(A)$
the stable category of all MCM
$\underline{\mathrm{CM}}(A)$
the stable category of all MCM
![]() $A$
-modules. Let
$A$
-modules. Let
![]() $M$
and
$M$
and
![]() $N$
be MCM
$N$
be MCM
![]() $A$
-modules. It is well known that we have a natural isomorphism:
$A$
-modules. It is well known that we have a natural isomorphism:
We denote
![]() $\eta ^{-1}(T_A(\Omega ^{-1}(M),N))$
by
$\eta ^{-1}(T_A(\Omega ^{-1}(M),N))$
by
![]() $\mathcal{R}(M,N)$
. Then
$\mathcal{R}(M,N)$
. Then
![]() $\eta$
induces the following isomorphism:
$\eta$
induces the following isomorphism:
Surprisingly,
Proposition 1.9.
![]() $\mathcal{R}$
is a relation on
$\mathcal{R}$
is a relation on
![]() $\underline{\mathrm{CM}}(A)$
.
$\underline{\mathrm{CM}}(A)$
.
Thus, we may consider the quotient category
![]() $\mathcal{D}_A = \underline{\mathrm{CM}}(A)/\mathcal{R}$
. Clearly,
$\mathcal{D}_A = \underline{\mathrm{CM}}(A)/\mathcal{R}$
. Clearly,
![]() $\mathcal{D}_A$
is a Hom-finite additive category. Surprisingly, the following result holds.
$\mathcal{D}_A$
is a Hom-finite additive category. Surprisingly, the following result holds.
Theorem 1.10.
Let
![]() $(A,\mathfrak{m})$
be a Henselian Gorenstein local ring and let
$(A,\mathfrak{m})$
be a Henselian Gorenstein local ring and let
![]() $M$
and
$M$
and
![]() $N$
be MCM
$N$
be MCM
![]() $A$
-modules. Then the following holds
$A$
-modules. Then the following holds
-
(1)
 $M\cong N$
in
$M\cong N$
in
 $\mathcal{D}_A$
if and only if
$\mathcal{D}_A$
if and only if
 $M\cong N$
in
$M\cong N$
in
 $\underline{\mathrm{CM}}(A)$
.
$\underline{\mathrm{CM}}(A)$
. -
(2)
 $M$
is indecomposable in
$M$
is indecomposable in
 $\mathcal{D}_A$
if and only if
$\mathcal{D}_A$
if and only if
 $M$
is indecomposable in
$M$
is indecomposable in
 $\underline{\mathrm{CM}}(A)$
$\underline{\mathrm{CM}}(A)$
-
(3)
 $\mathcal{D}_A$
is a Krull–Remak–Schmidt (KRS) category.
$\mathcal{D}_A$
is a Krull–Remak–Schmidt (KRS) category.
The main application of
![]() $T$
-split sequences was to study Weak Brauer–Thrall-II for associated graded modules (Recall Weak Brauer–Thrall-II: Do there exist distinct indecomposable MCM modules
$T$
-split sequences was to study Weak Brauer–Thrall-II for associated graded modules (Recall Weak Brauer–Thrall-II: Do there exist distinct indecomposable MCM modules
![]() $\{M_n\}_{n\geq 1}$
with
$\{M_n\}_{n\geq 1}$
with
![]() $G(M_n)$
Cohen–Macaulay and
$G(M_n)$
Cohen–Macaulay and
![]() $e(M_n)$
bounded?) for a large class of rings. Note that in [Reference Puthenpurakal20], the concept was introduced only for the
$e(M_n)$
bounded?) for a large class of rings. Note that in [Reference Puthenpurakal20], the concept was introduced only for the
![]() $\mathfrak{m}$
-adic filtration, but for general
$\mathfrak{m}$
-adic filtration, but for general
![]() $I(\ne \mathfrak{m})$
-adic filtrations that method will not work (see [Reference Puthenpurakal20, Remark 3.2]).
$I(\ne \mathfrak{m})$
-adic filtrations that method will not work (see [Reference Puthenpurakal20, Remark 3.2]).
In this article, we extend the results in [Reference Puthenpurakal20] to a large family of filtrations. Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d \geq 1$
and let
$d \geq 1$
and let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal. Let
$\mathfrak{m}$
-primary ideal. Let
![]() $\mathcal{F}=\{I_n\}_{n \in \mathbb{Z}}$
where
$\mathcal{F}=\{I_n\}_{n \in \mathbb{Z}}$
where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n=\overline{I^{n}}$
for
$I_n=\overline{I^{n}}$
for
![]() $n\gg 0$
be an
$n\gg 0$
be an
![]() $I$
-admissible filtration. Note here “–” denotes the integral closure. Let
$I$
-admissible filtration. Note here “–” denotes the integral closure. Let
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module.
$A$
-module.
Theorem 1.11. Set
Then
![]() $e_{\mathcal{F}}^T(M) = 0$
if and only if
$e_{\mathcal{F}}^T(M) = 0$
if and only if
![]() $M$
is free (see [Reference Kadu and Puthenpurakal13, Theorem 7.5]). Let
$M$
is free (see [Reference Kadu and Puthenpurakal13, Theorem 7.5]). Let
![]() $M,N$
be maximal Cohen–Macaulay
$M,N$
be maximal Cohen–Macaulay
![]() $A$
-modules and
$A$
-modules and
![]() $\alpha \in$
Ext
$\alpha \in$
Ext
![]() $_A^1(M,N)$
. Let
$_A^1(M,N)$
. Let
![]() $\alpha$
be given by an extension
$\alpha$
be given by an extension
![]() $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
; here,
$0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
; here,
![]() $E$
is a maximal Cohen–Macaulay module. Now set
$E$
is a maximal Cohen–Macaulay module. Now set
It can be shown that
![]() $e_{\mathcal{F}}^T(\alpha ) \geq 0$
, see 3.6.
$e_{\mathcal{F}}^T(\alpha ) \geq 0$
, see 3.6.
Definition 1.12. An extension
![]() $s\in \mathrm{Ext}_A^1(M,N)$
is
$s\in \mathrm{Ext}_A^1(M,N)$
is
![]() $T_{\mathcal{F}}$
-split if
$T_{\mathcal{F}}$
-split if
![]() $e_{\mathcal{F}}^T(s)=0$
.
$e_{\mathcal{F}}^T(s)=0$
.
As before we can show that
![]() ${T_{\mathcal{F}}}(M,N)$
is a submodule of
${T_{\mathcal{F}}}(M,N)$
is a submodule of
![]() $\mathrm{Ext}^1_A(M,N)$
(see 4.1). Furthermore,
$\mathrm{Ext}^1_A(M,N)$
(see 4.1). Furthermore,
![]() ${T_{\mathcal{F}}} \colon{\mathrm{CM}}(-)\times{\mathrm{CM}}(-) \rightarrow \mathrm{mod}(A)$
is a sub-functor of
${T_{\mathcal{F}}} \colon{\mathrm{CM}}(-)\times{\mathrm{CM}}(-) \rightarrow \mathrm{mod}(A)$
is a sub-functor of
![]() $\mathrm{Ext}^1_A(-,-)$
, see 4.2.
$\mathrm{Ext}^1_A(-,-)$
, see 4.2.
Theorem 1.13.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d$
with one of the following conditions:
$d$
with one of the following conditions:
-
(1) the residue field
 $k (= A/\mathfrak{m})$
is uncountable.
$k (= A/\mathfrak{m})$
is uncountable.
-
(2) the residue field
 $k$
is perfect field.
$k$
is perfect field.
Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
where
$\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n= \overline{I^{n}}$
for
$I_n= \overline{I^{n}}$
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $M, N$
be MCM
$M, N$
be MCM
![]() $A$
-module then
$A$
-module then
![]() $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
$\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
Next, we prove following theorem.
Theorem 1.14.
Let
![]() $(A,\mathfrak{m})$
be a complete reduced Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be a complete reduced Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
with either uncountable residue field or a perfect residue field. Let
$d\geq 1$
with either uncountable residue field or a perfect residue field. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal. Set
$\mathfrak{m}$
-primary ideal. Set
![]() $R=A[[X_1,\ldots, X_m]]$
,
$R=A[[X_1,\ldots, X_m]]$
,
![]() $J=(I,X_1,\ldots, X_m)$
,
$J=(I,X_1,\ldots, X_m)$
,
![]() $\mathcal{I}=\{\overline{I^n}\}_{n \in \mathbb{Z}}$
, and
$\mathcal{I}=\{\overline{I^n}\}_{n \in \mathbb{Z}}$
, and
![]() $\mathcal{J}=\{\overline{J^n}\}_{n \in \mathbb{Z}}$
. If
$\mathcal{J}=\{\overline{J^n}\}_{n \in \mathbb{Z}}$
. If
![]() $A$
has an MCM module
$A$
has an MCM module
![]() $M$
with
$M$
with
![]() $G_{\mathcal{I}}(M)$
Cohen–Macaulay. Then there exists
$G_{\mathcal{I}}(M)$
Cohen–Macaulay. Then there exists
![]() $\{ E_n \}_{n \geq 1}$
indecomposable MCM
$\{ E_n \}_{n \geq 1}$
indecomposable MCM
![]() $R$
-modules with bounded multiplicity (with respect to
$R$
-modules with bounded multiplicity (with respect to
![]() $\mathcal{J}$
) and having
$\mathcal{J}$
) and having
![]() $G_{\mathcal{J}}(E_n)$
Cohen–Macaulay for all
$G_{\mathcal{J}}(E_n)$
Cohen–Macaulay for all
![]() $n \geq 1$
.
$n \geq 1$
.
Let
![]() $e^T_{\mathcal{F}} \colon \mathrm{Ext}_A^1(M, N) \rightarrow \mathbb{N}$
be the function defined by
$e^T_{\mathcal{F}} \colon \mathrm{Ext}_A^1(M, N) \rightarrow \mathbb{N}$
be the function defined by
![]() $\alpha \mapsto e^T_{\mathcal{F}}(\alpha )$
. When
$\alpha \mapsto e^T_{\mathcal{F}}(\alpha )$
. When
![]() $A$
has characteristic
$A$
has characteristic
![]() $p \gt 0$
, then we can say more about this function. If
$p \gt 0$
, then we can say more about this function. If
![]() $V$
is a vector space over a field
$V$
is a vector space over a field
![]() $k$
, then let
$k$
, then let
![]() $\mathbb{P}(V)$
denote the projective space determined by
$\mathbb{P}(V)$
denote the projective space determined by
![]() $V$
.
$V$
.
Theorem 1.15.
(with hypotheses as in
1.13
) Further assume
![]() $A$
is of characteristic
$A$
is of characteristic
![]() $p \gt 0$
and that
$p \gt 0$
and that
![]() $A$
contains a field
$A$
contains a field
![]() $k \cong A/{\mathfrak{m}}$
. If
$k \cong A/{\mathfrak{m}}$
. If
![]() $\mathrm{Ext}_A^1(M, N) \neq T_{\mathcal{F}}(M,N)$
, then the function
$\mathrm{Ext}_A^1(M, N) \neq T_{\mathcal{F}}(M,N)$
, then the function
![]() $e^T_{\mathcal{F}}$
factors as:
$e^T_{\mathcal{F}}$
factors as:
We now describe in brief the contents of this paper. In section 2, we discuss some preliminary results. In section 3, we introduce our function 1.11 and discuss few of its properties. We also discuss in detail the base changes that we need to prove our results. In section 4, we prove Theorem1.13. In the next section, we prove Theorem1.14. In section 6, we prove Theorem1.15. In the next section, we discuss our result on relation between T-split sequences and AR-sequences. In section 8, we prove Theorem1.5. In the next section, we prove Theorem1.6 and construct Example 1.7. In section 10, we prove Proposition 1.9 and Theorem 1.10.
2. Preliminaries
Theorem 2.1. Let
![]() $(A,\mathfrak{m})$
be a Noetherian local ring and
$(A,\mathfrak{m})$
be a Noetherian local ring and
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal. Then a filtration
$\mathfrak{m}$
-primary ideal. Then a filtration
![]() $\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$
is said to be
$\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$
is said to be
![]() $I$
-admissible filtration if
$I$
-admissible filtration if
-
1.
 $I^n\subseteq F_n$
for all
$I^n\subseteq F_n$
for all
 $n$
.
$n$
. -
2.
 $F_nF_m \subseteq F_{n + m}$
for all
$F_nF_m \subseteq F_{n + m}$
for all
 $n,m \in \mathbb{Z}$
.
$n,m \in \mathbb{Z}$
. -
3.
 $F_n = IF_{n-1}$
for
$F_n = IF_{n-1}$
for
 $n\gg 0$
.
$n\gg 0$
.
Definition 2.2. A Noetherian local ring
![]() $(A,\mathfrak{m})$
is said to be analytically unramified if its
$(A,\mathfrak{m})$
is said to be analytically unramified if its
![]() $\mathfrak{m}$
-adic completion is reduced.
$\mathfrak{m}$
-adic completion is reduced.
Theorem 2.3.
Let
![]() $\overline{\mathfrak{a}}$
denote integral closure of the ideal
$\overline{\mathfrak{a}}$
denote integral closure of the ideal
![]() $\mathfrak{a}$
. If
$\mathfrak{a}$
. If
![]() $A$
is analytically unramified then from a result of Rees [Reference Rees21], the integral closure filtration
$A$
is analytically unramified then from a result of Rees [Reference Rees21], the integral closure filtration
![]() $\mathcal{F}=\{\overline{I^n}\}_{n \in \mathbb{Z}}$
is
$\mathcal{F}=\{\overline{I^n}\}_{n \in \mathbb{Z}}$
is
![]() $I$
-admissible.
$I$
-admissible.
Theorem 2.4.
Let
![]() $(A,\mathfrak{m})$
be a Noetherian local ring,
$(A,\mathfrak{m})$
be a Noetherian local ring,
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal, and
$\mathfrak{m}$
-primary ideal, and
![]() $\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$
a
$\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$
a
![]() $I$
-admissible filtration. Let
$I$
-admissible filtration. Let
![]() $M$
be a finite
$M$
be a finite
![]() $A$
-module with dimension
$A$
-module with dimension
![]() $r$
. Then the numerical function
$r$
. Then the numerical function
![]() $H_{\mathcal{F}}(M,n)= \ell (M/{F_{n+1}}M)$
is known as the Hilbert function of
$H_{\mathcal{F}}(M,n)= \ell (M/{F_{n+1}}M)$
is known as the Hilbert function of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathcal{F}$
. For large value of
$\mathcal{F}$
. For large value of
![]() $n$
,
$n$
,
![]() $H_{\mathcal{F}}(M,n)$
coincides with a polynomial
$H_{\mathcal{F}}(M,n)$
coincides with a polynomial
![]() $P_{\mathcal{F}}(M,n)$
of degree
$P_{\mathcal{F}}(M,n)$
of degree
![]() $r$
, and this polynomial is known as the Hilbert polynomial of
$r$
, and this polynomial is known as the Hilbert polynomial of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathcal{F}$
. There exist unique integer
$\mathcal{F}$
. There exist unique integer
![]() $e_0^{\mathcal{F}}(M),e_1^{\mathcal{F}}(M),\ldots, e_r^{\mathcal{F}}(M)$
such that Hilbert polynomial of
$e_0^{\mathcal{F}}(M),e_1^{\mathcal{F}}(M),\ldots, e_r^{\mathcal{F}}(M)$
such that Hilbert polynomial of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathcal{F}$
can be written as:
$\mathcal{F}$
can be written as:
These integers
![]() $e_0^{\mathcal{F}}(M),e_1^{\mathcal{F}}(M),\ldots, e_r^{\mathcal{F}}(M)$
are known as the Hilbert coefficients of
$e_0^{\mathcal{F}}(M),e_1^{\mathcal{F}}(M),\ldots, e_r^{\mathcal{F}}(M)$
are known as the Hilbert coefficients of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathcal{F}$
. In case of
$\mathcal{F}$
. In case of
![]() $\mathfrak{m}$
-adic and
$\mathfrak{m}$
-adic and
![]() $I$
-adic filtrations, these coefficients will be denoted as
$I$
-adic filtrations, these coefficients will be denoted as
![]() $e_i(M)$
and
$e_i(M)$
and
![]() $e_i^I(M)$
for
$e_i^I(M)$
for
![]() $i=1,\ldots, r$
, respectively.
$i=1,\ldots, r$
, respectively.
Theorem 2.5. Let
![]() $(A,\mathfrak{m})$
be a Noetherian local ring and
$(A,\mathfrak{m})$
be a Noetherian local ring and
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal. Let
$\mathfrak{m}$
-primary ideal. Let
![]() $\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$
be an
$\mathcal{F}=\{F_n\}_{n\in \mathbb{Z}}$
be an
![]() $I$
-admissible filtration and
$I$
-admissible filtration and
![]() $M$
an
$M$
an
![]() $A$
-module with positive dimension. Then an element
$A$
-module with positive dimension. Then an element
![]() $x\in F_1\setminus F_2$
is said to be
$x\in F_1\setminus F_2$
is said to be
![]() $\mathcal{F}$
-superficial element for
$\mathcal{F}$
-superficial element for
![]() $M$
if there exists
$M$
if there exists
![]() $c\in \mathbb{N}$
such that for all
$c\in \mathbb{N}$
such that for all
![]() $n\geq c$
,
$n\geq c$
,
The following facts are well known:
-
1. If
 $k= A/\mathfrak{m}$
is infinite, then
$k= A/\mathfrak{m}$
is infinite, then
 $\mathcal{F}$
-superficial elements for
$\mathcal{F}$
-superficial elements for
 $M$
exist.
$M$
exist. -
2. If
 $\mathrm{depth}\; M\gt 0$
, then every
$\mathrm{depth}\; M\gt 0$
, then every
 $\mathcal{F}$
-superficial element for
$\mathcal{F}$
-superficial element for
 $M$
is also
$M$
is also
 $M$
-regular.
$M$
-regular. -
3. If
 $x$
is
$x$
is
 $\mathcal{F}$
-superficial element for
$\mathcal{F}$
-superficial element for
 $M$
and
$M$
and
 $\mathrm{depth} M \gt 0$
, then
$\mathrm{depth} M \gt 0$
, then
 $(F_{n+1}M:_Mx)= F_nM$
for
$(F_{n+1}M:_Mx)= F_nM$
for
 $n\gg 0$
.
$n\gg 0$
. -
4. If
 $x$
is
$x$
is
 $\mathcal{F}$
-superficial element for
$\mathcal{F}$
-superficial element for
 $M$
and
$M$
and
 $\mathrm{depth} M \gt 0$
, then
$\mathrm{depth} M \gt 0$
, then
 $e_i^{\overline{\mathcal{F}}} (M/xM) = e_i^{\mathcal{F}}(M)$
for
$e_i^{\overline{\mathcal{F}}} (M/xM) = e_i^{\mathcal{F}}(M)$
for
 $i = 0,1,\ldots, \dim M - 1$
(here
$i = 0,1,\ldots, \dim M - 1$
(here
 $\overline{\mathcal{F}}$
is the obvious quotient filtration of
$\overline{\mathcal{F}}$
is the obvious quotient filtration of
 $\mathcal{F}$
).
$\mathcal{F}$
).
Theorem 2.6. A sequence
![]() $\underline{x}=x_1,\ldots, x_r$
with
$\underline{x}=x_1,\ldots, x_r$
with
![]() $r\leq \dim M$
is said to be
$r\leq \dim M$
is said to be
![]() $\mathcal{F}$
-superficial sequence for
$\mathcal{F}$
-superficial sequence for
![]() $M$
if
$M$
if
![]() $x_1$
is
$x_1$
is
![]() $\mathcal{F}$
-superficial element for
$\mathcal{F}$
-superficial element for
![]() $M$
and
$M$
and
![]() $x_i$
is
$x_i$
is
![]() $\mathcal{F}/(x_1,\ldots, x_{i-1})$
-superficial element for
$\mathcal{F}/(x_1,\ldots, x_{i-1})$
-superficial element for
![]() $M/(x_1,\ldots, x_{i-1})M$
for all
$M/(x_1,\ldots, x_{i-1})M$
for all
![]() $i\leq r$
.
$i\leq r$
.
3. The case when
 $A$
is analytically unramified
$A$
is analytically unramified
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring with
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring with
![]() $\dim A = d\geq 1$
and
$\dim A = d\geq 1$
and
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal. We are primarily interested in the integral closure filtration of
$\mathfrak{m}$
-primary ideal. We are primarily interested in the integral closure filtration of
![]() $I$
. However, to prove our results, we need the following class of
$I$
. However, to prove our results, we need the following class of
![]() $I$
-admissible filtrations
$I$
-admissible filtrations
![]() $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
, where
$\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
, where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n=\overline{I^n}$
for
$I_n=\overline{I^n}$
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module.
$A$
-module.
Theorem 3.1. The numerical function
is polynomial type; that is, there is a polynomial
![]() $t^A_{\mathcal{F}}(M,z)$
which coincides with this numerical function for
$t^A_{\mathcal{F}}(M,z)$
which coincides with this numerical function for
![]() $n\gg 0$
.
$n\gg 0$
.
If
![]() $M$
is non-free MCM
$M$
is non-free MCM
![]() $A$
-module, then
$A$
-module, then
![]() $\deg t^A_{\mathcal{F}}(M,z)=d-1$
(see [Reference Kadu and Puthenpurakal13, Theorem 7.5]). Note that normalized leading coefficient of
$\deg t^A_{\mathcal{F}}(M,z)=d-1$
(see [Reference Kadu and Puthenpurakal13, Theorem 7.5]). Note that normalized leading coefficient of
![]() $t^A_{\mathcal{F}}(M,z)$
is
$t^A_{\mathcal{F}}(M,z)$
is
![]() $e_1^{\mathcal{F}}(A)\mu (M)-e_1^{\mathcal{F}}(M)-e_1^{\mathcal{F}}(\text{Syz}_1^A(M))$
.
$e_1^{\mathcal{F}}(A)\mu (M)-e_1^{\mathcal{F}}(M)-e_1^{\mathcal{F}}(\text{Syz}_1^A(M))$
.
Theorem 3.2. Set
 \begin{align*} e_{\mathcal{F}}^T(M)&=\lim _{n\to \infty }\frac{(d-1)!}{n^{d-1}}\ell ({\mathrm{Tor}}_1^A(M,A/{I_{n+1}}))\\ &=e_1^{\mathcal{F}}(A)\mu (M)-e_1^{\mathcal{F}}(M)-e_1^{\mathcal{F}}(\text{Syz}_1^A(M)) \end{align*}
\begin{align*} e_{\mathcal{F}}^T(M)&=\lim _{n\to \infty }\frac{(d-1)!}{n^{d-1}}\ell ({\mathrm{Tor}}_1^A(M,A/{I_{n+1}}))\\ &=e_1^{\mathcal{F}}(A)\mu (M)-e_1^{\mathcal{F}}(M)-e_1^{\mathcal{F}}(\text{Syz}_1^A(M)) \end{align*}
Theorem 3.3. Base change: We need to do several base changes in our arguments.
(I) We first discuss the general setup: Let
![]() $\psi \colon (A,{\mathfrak{m}})\rightarrow (B,\mathfrak{n})$
be a flat map such that
$\psi \colon (A,{\mathfrak{m}})\rightarrow (B,\mathfrak{n})$
be a flat map such that
![]() $B$
is also a Cohen–Macaulay local ring and
$B$
is also a Cohen–Macaulay local ring and
![]() $({\mathfrak{m}} B =\mathfrak{n}$
. If
$({\mathfrak{m}} B =\mathfrak{n}$
. If
![]() $M$
is an
$M$
is an
![]() $A$
-module, then set
$A$
-module, then set
![]() $M_B= M\otimes _A B$
. If
$M_B= M\otimes _A B$
. If
![]() $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
is an
$\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
is an
![]() $I$
-admissible filtration, then set
$I$
-admissible filtration, then set
![]() $\mathcal{F}_B=\{{I_n B}\}_{n \in \mathbb{Z}}$
. Then,
$\mathcal{F}_B=\{{I_n B}\}_{n \in \mathbb{Z}}$
. Then,
-
1.
 $\ell (N)=\ell (N_B)$
for any finite length
$\ell (N)=\ell (N_B)$
for any finite length
 $A$
-module
$A$
-module
 $N$
.
$N$
. -
2.
 $\mathcal{F}_B$
is an
$\mathcal{F}_B$
is an
 $IB$
-admissible filtration.
$IB$
-admissible filtration. -
3.
 $\dim M= \dim M_B$
and
$\dim M= \dim M_B$
and
 $\mathrm{depth} M = \mathrm{depth} M_B$
. In particular,
$\mathrm{depth} M = \mathrm{depth} M_B$
. In particular,
 $M$
is an MCM
$M$
is an MCM
 $A$
-module if and only if
$A$
-module if and only if
 $M_B$
is MCM
$M_B$
is MCM
 $B$
-module.
$B$
-module. -
4. Syz
 $^A_i(M)\otimes _A B\cong \text{Syz}^B_i(M_B)$
for all
$^A_i(M)\otimes _A B\cong \text{Syz}^B_i(M_B)$
for all
 $i \geq 0$
.
$i \geq 0$
. -
5.
 $e_i^{\mathcal{F}}(M)= e_i^{\mathcal{F}_B}(M_B)$
for all
$e_i^{\mathcal{F}}(M)= e_i^{\mathcal{F}_B}(M_B)$
for all
 $i$
.
$i$
. -
6. If
 $\psi$
is regular and
$\psi$
is regular and
 $\mathfrak{a}$
is integrally closed
$\mathfrak{a}$
is integrally closed
 $\mathfrak{m}$
-primary ideal in
$\mathfrak{m}$
-primary ideal in
 $A$
, then
$A$
, then
 $\mathfrak{a}B$
is integrally closed in
$\mathfrak{a}B$
is integrally closed in
 $B$
(for instance, see [Reference Heinzer, Rotthaus and Wiegand11, 2.2(7)]).
$B$
(for instance, see [Reference Heinzer, Rotthaus and Wiegand11, 2.2(7)]).
(II) Assume
![]() $A$
is analytically unramified Cohen–Macaulay local ring and
$A$
is analytically unramified Cohen–Macaulay local ring and
![]() $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
is an
$\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
is an
![]() $I$
-admissible filtration with
$I$
-admissible filtration with
![]() $I$
,
$I$
,
![]() $\mathfrak{m}$
-primary and furthermore
$\mathfrak{m}$
-primary and furthermore
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n=\overline{I^n}$
for
$I_n=\overline{I^n}$
for
![]() $n\gg 0$
. We need to base changes as above where
$n\gg 0$
. We need to base changes as above where
![]() $\mathcal{F}_B$
has the property that
$\mathcal{F}_B$
has the property that
![]() $I_nB = I^nB = \overline{I^nB}$
whenever
$I_nB = I^nB = \overline{I^nB}$
whenever
![]() $I_n = \overline{I^n}$
. Note this automatically forces
$I_n = \overline{I^n}$
. Note this automatically forces
![]() $B$
to be analytically unramified. The specific base changes we do are the following:
$B$
to be analytically unramified. The specific base changes we do are the following:
-
(i)
 $B = \widehat{A}$
the completion of
$B = \widehat{A}$
the completion of
 $A$
. Note that if
$A$
. Note that if
 $J$
is an
$J$
is an
 $\mathfrak{m}$
-primary integrally closed ideal, then
$\mathfrak{m}$
-primary integrally closed ideal, then
 $J\widehat{A}$
is also integrally closed, cf., [Reference Huneke and Swanson12, 9.1.1].
$J\widehat{A}$
is also integrally closed, cf., [Reference Huneke and Swanson12, 9.1.1]. -
(ii) If
 $A$
has a finite residue field, then we can consider the extension
$A$
has a finite residue field, then we can consider the extension
 $B = A[X]_{({\mathfrak{m}} A[X]}$
. The residue field of
$B = A[X]_{({\mathfrak{m}} A[X]}$
. The residue field of
 $B$
is
$B$
is
 $k(X)$
which is infinite. Note that if
$k(X)$
which is infinite. Note that if
 $J$
is an
$J$
is an
 $\mathfrak{m}$
-primary integrally closed ideal, then
$\mathfrak{m}$
-primary integrally closed ideal, then
 $J\widehat{A}$
is also integrally closed, cf., [Reference Huneke and Swanson12, 8.4.2].
$J\widehat{A}$
is also integrally closed, cf., [Reference Huneke and Swanson12, 8.4.2]. -
(iii) Assume
 $\dim A \geq 2$
. Even if
$\dim A \geq 2$
. Even if
 $A$
has infinite residue field, there might not exist an
$A$
has infinite residue field, there might not exist an
 $\mathcal{F}$
-superficial element
$\mathcal{F}$
-superficial element
 $x$
such that
$x$
such that
 $A/(x)$
is analytically unramified. However, a suitable extension
$A/(x)$
is analytically unramified. However, a suitable extension
 $B$
has this property. To see this, we first observe two facts.
$B$
has this property. To see this, we first observe two facts.
Let
![]() $\mathcal{E}$
be a countable set of MCM of
$\mathcal{E}$
be a countable set of MCM of
![]() $A$
-modules. Assume that the residue field
$A$
-modules. Assume that the residue field
![]() $k$
of
$k$
of
![]() $A$
is uncountable if
$A$
is uncountable if
![]() $\mathcal{E}$
is an infinite set. Otherwise,
$\mathcal{E}$
is an infinite set. Otherwise,
![]() $k$
is infinite.
$k$
is infinite.
-
(a) There exist
 $\underline{x}=x_1,\ldots, x_d\in \overline{I}$
such that
$\underline{x}=x_1,\ldots, x_d\in \overline{I}$
such that
 $\underline{x}$
is
$\underline{x}$
is
 $\mathcal{F}$
-superficial for each
$\mathcal{F}$
-superficial for each
 $N \in \mathcal{E}$
. This result is well known (for instance, see [Reference Puthenpurakal18, Lemma 2.2]).
$N \in \mathcal{E}$
. This result is well known (for instance, see [Reference Puthenpurakal18, Lemma 2.2]). -
(b) There exists a generating set
 $r_1,\ldots, r_t$
of
$r_1,\ldots, r_t$
of
 $I$
such that for each
$I$
such that for each
 $i$
,
$i$
,
 $r_i$
is
$r_i$
is
 $I$
-superficial and
$I$
-superficial and
 $\mathcal{F}$
-superficial element for each
$\mathcal{F}$
-superficial element for each
 $N \in \mathcal{E}$
(see (a) and [Reference Kadu and Puthenpurakal13, Lemma 7.3]).
$N \in \mathcal{E}$
(see (a) and [Reference Kadu and Puthenpurakal13, Lemma 7.3]).
([Reference Ciupercă7 ], [Reference Kadu and Puthenpurakal13, Lemma 7.4, Theorem 7.5]) Choose
![]() $r_1,\ldots, r_t$
as in (b). Now consider following flat extension of rings
$r_1,\ldots, r_t$
as in (b). Now consider following flat extension of rings
Let
![]() $\zeta = r_1X_1+\ldots +r_tX_t$
. Set
$\zeta = r_1X_1+\ldots +r_tX_t$
. Set
![]() $C = B/\zeta B$
and
$C = B/\zeta B$
and
![]() $\mathcal{F}_C=\{I_n C\}$
. For
$\mathcal{F}_C=\{I_n C\}$
. For
![]() $N \in \mathcal{E}$
, set
$N \in \mathcal{E}$
, set
![]() $N_B = N\otimes _A B$
. Then, we have
$N_B = N\otimes _A B$
. Then, we have
-
1.
 $B$
is analytically unramified Cohen–Macaulay local ring of dimension
$B$
is analytically unramified Cohen–Macaulay local ring of dimension
 $d$
.
$d$
. -
2.
 $N_B$
is MCM
$N_B$
is MCM
 $B$
-module for each
$B$
-module for each
 $N \in \mathcal{E}$
.
$N \in \mathcal{E}$
. -
3. If
 $J$
is a integrally closed
$J$
is a integrally closed
 $\mathfrak{m}$
-primary ideal in
$\mathfrak{m}$
-primary ideal in
 $A$
, then
$A$
, then
 $JB$
a integrally closed
$JB$
a integrally closed
 $\mathfrak{n}$
-primary ideal in
$\mathfrak{n}$
-primary ideal in
 $B$
.
$B$
. -
4.
 $I_1C = \overline{I}C = \overline{IC}$
.
$I_1C = \overline{I}C = \overline{IC}$
. -
5.
 $I_nC=\overline{I^nC}$
for all
$I_nC=\overline{I^nC}$
for all
 $n\gg 0$
.
$n\gg 0$
. -
6.
 $C$
is analytically unramified Cohen–Macaulay local ring of dimension
$C$
is analytically unramified Cohen–Macaulay local ring of dimension
 $d-1$
.
$d-1$
. -
7.
 $\zeta$
is
$\zeta$
is
 $\mathcal{F}_B$
-superficial for each
$\mathcal{F}_B$
-superficial for each
 $N_B$
(here
$N_B$
(here
 $N \in \mathcal{E}$
).
$N \in \mathcal{E}$
).
-
(iv) For some of our arguments, we need the residue field of
 $A$
to be uncountable. If
$A$
to be uncountable. If
 $k$
is finite or countably infinite perfect field do the following: First complete
$k$
is finite or countably infinite perfect field do the following: First complete
 $A$
. By (i), this is possible. So, we may assume
$A$
. By (i), this is possible. So, we may assume
 $A$
is complete.
$A$
is complete.
Consider extension
![]() $\phi \;:\; A\longrightarrow A[[X]]_{\mathfrak{m}A[[X]]}=(B,\mathfrak{n})$
. Set
$\phi \;:\; A\longrightarrow A[[X]]_{\mathfrak{m}A[[X]]}=(B,\mathfrak{n})$
. Set
![]() $B_0=B\otimes _Ak=B/\mathfrak{m}B$
. So,
$B_0=B\otimes _Ak=B/\mathfrak{m}B$
. So,
![]() $B_0=B/\mathfrak{n}=k((X))$
is uncountable. As
$B_0=B/\mathfrak{n}=k((X))$
is uncountable. As
![]() $k$
is perfect we get
$k$
is perfect we get
![]() $k((X))$
is
$k((X))$
is
![]() $0$
-smooth over
$0$
-smooth over
![]() $k$
, see [Reference Matsumura14, 28.7]. Using [Reference Matsumura14, 28.10], we get
$k$
, see [Reference Matsumura14, 28.7]. Using [Reference Matsumura14, 28.10], we get
![]() $B$
is
$B$
is
![]() $\mathfrak{n} (=\mathfrak{m}B)$
-smooth. This implies
$\mathfrak{n} (=\mathfrak{m}B)$
-smooth. This implies
![]() $\phi$
is regular (see [Reference André1, Theorem]).
$\phi$
is regular (see [Reference André1, Theorem]).
By I(6) if
![]() $\mathfrak{a}$
is an integrally closed
$\mathfrak{a}$
is an integrally closed
![]() $\mathfrak{m}$
-primary ideal in
$\mathfrak{m}$
-primary ideal in
![]() $A$
, then
$A$
, then
![]() $\mathfrak{a} B$
is integrally closed in
$\mathfrak{a} B$
is integrally closed in
![]() $B$
. Thus,
$B$
. Thus,
![]() ${I_n}B=\overline{I^nB}$
whenever
${I_n}B=\overline{I^nB}$
whenever
![]() $I_n = \overline{I^n}$
.
$I_n = \overline{I^n}$
.
Definition 3.4. We say a flat extension
![]() $\psi \colon (A,{\mathfrak{m}}) \rightarrow (B,\mathfrak{n})$
with
$\psi \colon (A,{\mathfrak{m}}) \rightarrow (B,\mathfrak{n})$
with
![]() ${\mathfrak{m}} B = \mathfrak{n}$
behaves well with respect to integral closure if for any integrally closed
${\mathfrak{m}} B = \mathfrak{n}$
behaves well with respect to integral closure if for any integrally closed
![]() $\mathfrak{m}$
-
primary ideal
$\mathfrak{m}$
-
primary ideal
![]() $\mathfrak{a}$
in
$\mathfrak{a}$
in
![]() $A$
, the ideal
$A$
, the ideal
![]() $\mathfrak{a} B$
is integrally closed in
$\mathfrak{a} B$
is integrally closed in
![]() $B$
.
$B$
.
We need the following result:
Proposition 3.5.
Let
![]() $(A,\mathfrak{m})$
be analytically unramified Cohen–Macaulay local ring with
$(A,\mathfrak{m})$
be analytically unramified Cohen–Macaulay local ring with
![]() $\dim A = d\geq 1$
and
$\dim A = d\geq 1$
and
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal. Let
$\mathfrak{m}$
-primary ideal. Let
![]() $\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
be a
$\mathcal{F}=\{{I_n}\}_{n \in \mathbb{Z}}$
be a
![]() $I$
-admissible filtration where
$I$
-admissible filtration where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n=\overline{I^n}$
for
$I_n=\overline{I^n}$
for
![]() $n\gg 0$
.
$n\gg 0$
.
-
(1) Let
 $(B,\mathfrak{n})$
be a flat extension of
$(B,\mathfrak{n})$
be a flat extension of
 $A$
which behaves well with respect to integral closure. Set
$A$
which behaves well with respect to integral closure. Set
 $\mathcal{F}_B = \{{I_nB}\}_{n \in \mathbb{Z}}$
. Then for any MCM
$\mathcal{F}_B = \{{I_nB}\}_{n \in \mathbb{Z}}$
. Then for any MCM
 $A$
-module
$A$
-module
 $M$
, we have
$M$
, we have
 $e^T_{\mathcal{F}}(M) = e^T_{\mathcal{F}_B}(M_B)$
.
$e^T_{\mathcal{F}}(M) = e^T_{\mathcal{F}_B}(M_B)$
. -
(2) Let
 $\dim A \geq 2$
. and the residue field of
$\dim A \geq 2$
. and the residue field of
 $A$
is infinite. Let
$A$
is infinite. Let
 $\mathcal{V}$
be any countable set of MCM
$\mathcal{V}$
be any countable set of MCM
 $A$
-modules (containing
$A$
-modules (containing
 $A$
). Assume
$A$
). Assume
 $k = A/{\mathfrak{m}}$
is uncountable if
$k = A/{\mathfrak{m}}$
is uncountable if
 $\mathcal{V}$
is infinite otherwise
$\mathcal{V}$
is infinite otherwise
 $k$
is infinite. Then there exists a flat extension
$k$
is infinite. Then there exists a flat extension
 $B$
of
$B$
of
 $A$
which behaves well with respect to integral closure such that there exist
$A$
which behaves well with respect to integral closure such that there exist
 $\zeta \in IB$
which is
$\zeta \in IB$
which is
 $\mathcal{F}_B$
-superficial with respect to each
$\mathcal{F}_B$
-superficial with respect to each
 $N_B$
(for all
$N_B$
(for all
 $N \in \mathcal{V}$
). Furthermore, if
$N \in \mathcal{V}$
). Furthermore, if
 $C = B/\zeta B$
then
$C = B/\zeta B$
then
 $C$
is analytically unramified with
$C$
is analytically unramified with
 $IC = \overline{IC}$
and
$IC = \overline{IC}$
and
 $I_nC = \overline{I^nC}$
for all
$I_nC = \overline{I^nC}$
for all
 $n \gg 0$
. Set
$n \gg 0$
. Set
 $N_C = N\otimes _A C$
. Furthermore,
$N_C = N\otimes _A C$
. Furthermore,
 $e^T_{\mathcal{F}}(N) = e^T_{\mathcal{F}_C}(N_C)$
for each
$e^T_{\mathcal{F}}(N) = e^T_{\mathcal{F}_C}(N_C)$
for each
 $N \in \mathcal{V}$
.
$N \in \mathcal{V}$
.
Proof. (1) This follows from 3.3(I).
(2) Set
![]() $\mathcal{E} = \{ \mathrm{Syz}^A_i(N) \colon i = 0, 1 \ \text{and} \ N \in \mathcal{V}\}$
. Then
$\mathcal{E} = \{ \mathrm{Syz}^A_i(N) \colon i = 0, 1 \ \text{and} \ N \in \mathcal{V}\}$
. Then
![]() $\mathcal{E}$
is a countable set and is finite if
$\mathcal{E}$
is a countable set and is finite if
![]() $\mathcal{V}$
is. Now do the construction in 3.3(I)(iii) and use 2.5(4) and 3.2 to conclude.
$\mathcal{V}$
is. Now do the construction in 3.3(I)(iii) and use 2.5(4) and 3.2 to conclude.
The following lemma follows from [Reference Puthenpurakal17, Theorem 2.6], but here we give a short proof (similar proof also works for
![]() ${e_{A}^T}()$
):
${e_{A}^T}()$
):
Lemma 3.6.
Let
![]() $\alpha : 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
be an exact sequence of MCM
$\alpha : 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
be an exact sequence of MCM
![]() $A$
-modules. Then
$A$
-modules. Then
![]() ${e_{\mathcal{F}}^T}(E)\leq{e_{\mathcal{F}}^T}(M)+{e_{\mathcal{F}}^T}(N)$
.
${e_{\mathcal{F}}^T}(E)\leq{e_{\mathcal{F}}^T}(M)+{e_{\mathcal{F}}^T}(N)$
.
Proof.
Consider the long exact sequence of
![]() $\alpha \otimes _A A/{{I_{n+1}}}$
. We get
$\alpha \otimes _A A/{{I_{n+1}}}$
. We get
So,
![]() $\ell ({\mathrm{Tor}}^A_1(E,A/{I_{n+1}}))\leq \ell ({\mathrm{Tor}}^A_1(M,A/{I_{n+1}})) + \ell ({\mathrm{Tor}}^A_1(N,A/{I_{n+1}}))$
. Now from the definition of
$\ell ({\mathrm{Tor}}^A_1(E,A/{I_{n+1}}))\leq \ell ({\mathrm{Tor}}^A_1(M,A/{I_{n+1}})) + \ell ({\mathrm{Tor}}^A_1(N,A/{I_{n+1}}))$
. Now from the definition of
![]() ${e_{\mathcal{F}}^T}(-)$
, required inequality follows.
${e_{\mathcal{F}}^T}(-)$
, required inequality follows.
Theorem 3.7.
Let
![]() $M,N$
be maximal Cohen–Macaulay
$M,N$
be maximal Cohen–Macaulay
![]() $A$
-modules and
$A$
-modules and
![]() $\alpha \in \mathrm{Ext}_A^1(M,N)$
. Let
$\alpha \in \mathrm{Ext}_A^1(M,N)$
. Let
![]() $\alpha$
be given by an extension
$\alpha$
be given by an extension
![]() $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
, here
$0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
, here
![]() $E$
is a maximal Cohen–Macaulay module. Now set
$E$
is a maximal Cohen–Macaulay module. Now set
Theorem 3.8.
Let
![]() $\alpha _1,\alpha _2\in \mathrm{Ext}^1_A(M,N)$
. Suppose
$\alpha _1,\alpha _2\in \mathrm{Ext}^1_A(M,N)$
. Suppose
![]() $\alpha _i$
can be given by
$\alpha _i$
can be given by
![]() $0\rightarrow N\rightarrow E_i\rightarrow M\rightarrow 0$
for
$0\rightarrow N\rightarrow E_i\rightarrow M\rightarrow 0$
for
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are equivalent, then
$\alpha _2$
are equivalent, then
![]() $E_1\cong E_2$
. So,
$E_1\cong E_2$
. So,
![]() ${e_{\mathcal{F}}^T}(\alpha _1)={e_{\mathcal{F}}^T}(\alpha _2)$
. This implies
${e_{\mathcal{F}}^T}(\alpha _1)={e_{\mathcal{F}}^T}(\alpha _2)$
. This implies
![]() ${e_{\mathcal{F}}^T}(\alpha )$
is well defined.
${e_{\mathcal{F}}^T}(\alpha )$
is well defined.
Note that
![]() ${e_{\mathcal{F}}^T}(\alpha )\geq 0$
.
${e_{\mathcal{F}}^T}(\alpha )\geq 0$
.
Definition 3.9. An extension
![]() $s\in$
Ext
$s\in$
Ext
![]() $_A^1(M,N)$
is
$_A^1(M,N)$
is
![]() $T_{\mathcal{F}}$
-split if
$T_{\mathcal{F}}$
-split if
![]() $e_{\mathcal{F}}^T(s)=0$
.
$e_{\mathcal{F}}^T(s)=0$
.
Definition 3.10. Let
![]() $M,N$
be maximal Cohen–Macaulay
$M,N$
be maximal Cohen–Macaulay
![]() $A$
-modules. Set
$A$
-modules. Set
Note that if the choice of the ring
![]() $A$
is unambiguous from the context, we denote this set as
$A$
is unambiguous from the context, we denote this set as
![]() ${T_{\mathcal{F}}}(M,N)$
.
${T_{\mathcal{F}}}(M,N)$
.
We will need the following two results:
Lemma 3.11.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
and let
$d\geq 1$
and let
![]() $M, N, N_1, E, E_1$
be MCM
$M, N, N_1, E, E_1$
be MCM
![]() $A$
-modules. Suppose we have a commutative diagram
$A$
-modules. Suppose we have a commutative diagram

If
![]() $\alpha$
is
$\alpha$
is
![]() $T_{\mathcal{F}}$
-split, then
$T_{\mathcal{F}}$
-split, then
![]() $\beta$
is also
$\beta$
is also
![]() $T_{\mathcal{F}}$
-split.
$T_{\mathcal{F}}$
-split.
Proof.
If
![]() $\dim A = 1$
, then we can give an argument similar to [Reference Puthenpurakal20, Proposition 3.8]. Now assume
$\dim A = 1$
, then we can give an argument similar to [Reference Puthenpurakal20, Proposition 3.8]. Now assume
![]() $d = \dim A \geq 2$
and the result has been proved for all analytically unramified rings of dimension
$d = \dim A \geq 2$
and the result has been proved for all analytically unramified rings of dimension
![]() $d -1$
. If the residue field of
$d -1$
. If the residue field of
![]() $A$
is finite, then use 3.3II.(ii). So, we may assume
$A$
is finite, then use 3.3II.(ii). So, we may assume
![]() $A/{\mathfrak{m}}$
is infinite. Using 3.5, we may assume that (after going to a flat extension) there exists
$A/{\mathfrak{m}}$
is infinite. Using 3.5, we may assume that (after going to a flat extension) there exists
![]() $\zeta \in I$
such that
$\zeta \in I$
such that
-
(i)
 $\zeta$
is
$\zeta$
is
 $\mathcal{F}$
-superficial with respect to
$\mathcal{F}$
-superficial with respect to
 $A\oplus U \oplus \mathrm{Syz}^A_1(U)$
for each
$A\oplus U \oplus \mathrm{Syz}^A_1(U)$
for each
 $U$
in the above diagram.
$U$
in the above diagram. -
(ii)
 $C = A/\zeta A$
is analytically unramified with
$C = A/\zeta A$
is analytically unramified with
 $IC = \overline{IC}$
and
$IC = \overline{IC}$
and
 $I_nC = \overline{I^nC}$
for all
$I_nC = \overline{I^nC}$
for all
 $n \gg 0$
.
$n \gg 0$
. -
(iii)
 $e^T_{\mathcal{F}_C}(U/\zeta U) = e^T_{\mathcal{F}}(U)$
for each
$e^T_{\mathcal{F}_C}(U/\zeta U) = e^T_{\mathcal{F}}(U)$
for each
 $U$
in the above diagram.
$U$
in the above diagram.
Notice
![]() $\alpha \otimes C$
and
$\alpha \otimes C$
and
![]() $\beta \otimes C$
are exact. For an
$\beta \otimes C$
are exact. For an
![]() $A$
-module
$A$
-module
![]() $V$
, set
$V$
, set
![]() $\overline{V} = V/\zeta V$
. So, we have a diagram
$\overline{V} = V/\zeta V$
. So, we have a diagram

Note
![]() $\alpha \otimes C$
is
$\alpha \otimes C$
is
![]() $T_{\mathcal{F}_C}$
-split. By our induction hypotheses,
$T_{\mathcal{F}_C}$
-split. By our induction hypotheses,
![]() $\beta \otimes C$
is
$\beta \otimes C$
is
![]() $T_{\mathcal{F}_C}$
-split. By our construction, it follows that
$T_{\mathcal{F}_C}$
-split. By our construction, it follows that
![]() $\beta$
is also
$\beta$
is also
![]() $T_{\mathcal{F}}$
-split.
$T_{\mathcal{F}}$
-split.
Lemma 3.12.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
and let
$d\geq 1$
and let
![]() $M, M_1, N, E, E_1$
be MCM
$M, M_1, N, E, E_1$
be MCM
![]() $A$
-modules. Suppose we have a commutative diagram
$A$
-modules. Suppose we have a commutative diagram

If
![]() $\beta$
is
$\beta$
is
![]() $T_{\mathcal{F}}$
-split, then
$T_{\mathcal{F}}$
-split, then
![]() $\alpha$
is also
$\alpha$
is also
![]() $T_{\mathcal{F}}$
-split.
$T_{\mathcal{F}}$
-split.
Proof. This is dual to 3.11.
4.
 $T_{\mathcal{F}}$
-split sequences
$T_{\mathcal{F}}$
-split sequences
In this section, we prove our results regarding
![]() $T_{\mathcal{F}}$
.
$T_{\mathcal{F}}$
.
Theorem 4.1.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d$
. Let
$d$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F}=\{{I_n}\}$
where
$\mathcal{F}=\{{I_n}\}$
where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n= \overline{I^{n}}$
for
$I_n= \overline{I^{n}}$
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $M, N$
be MCM
$M, N$
be MCM
![]() $A$
-module, then
$A$
-module, then
![]() ${T_{\mathcal{F}}}(M,N)$
is a submodule of
${T_{\mathcal{F}}}(M,N)$
is a submodule of
![]() $\mathrm{Ext}^1_A(M,N)$
.
$\mathrm{Ext}^1_A(M,N)$
.
Proof.
Let
![]() $\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
be a
$\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
be a
![]() $T_{\mathcal{F}}$
-split extension and
$T_{\mathcal{F}}$
-split extension and
![]() $r\in A$
, then we can define
$r\in A$
, then we can define
![]() $r\alpha$
$r\alpha$

Note that first square is pushout diagram. Since
![]() $\alpha$
is
$\alpha$
is
![]() $T_{\mathcal{F}}$
-split, this implies
$T_{\mathcal{F}}$
-split, this implies
![]() $r\alpha$
is also
$r\alpha$
is also
![]() $T_{\mathcal{F}}$
-split (see 3.11).
$T_{\mathcal{F}}$
-split (see 3.11).
Let
![]() $\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
and
$\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
and
![]() $\alpha' \;:\; 0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$
be two
$\alpha' \;:\; 0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$
be two
![]() $T_{\mathcal{F}}$
-split extensions. We want to show
$T_{\mathcal{F}}$
-split extensions. We want to show
![]() $\alpha +\alpha '$
is also
$\alpha +\alpha '$
is also
![]() $T_{\mathcal{F}}$
-split. Note that the addition operation on
$T_{\mathcal{F}}$
-split. Note that the addition operation on
![]() $\mathrm{Ext}^1_A(M,N)$
is Bear sum, that is,
$\mathrm{Ext}^1_A(M,N)$
is Bear sum, that is,
![]() $\alpha +\alpha ':= (\nabla (\alpha \oplus \alpha '))\Delta$
.
$\alpha +\alpha ':= (\nabla (\alpha \oplus \alpha '))\Delta$
.
Since
![]() $\alpha$
and
$\alpha$
and
![]() $\alpha '$
are
$\alpha '$
are
![]() $T_{\mathcal{F}}$
-split, this implies
$T_{\mathcal{F}}$
-split, this implies
![]() $\alpha \oplus \alpha '\;:\; 0\rightarrow N\oplus N\rightarrow E\oplus E'\rightarrow M\oplus M\rightarrow 0$
also
$\alpha \oplus \alpha '\;:\; 0\rightarrow N\oplus N\rightarrow E\oplus E'\rightarrow M\oplus M\rightarrow 0$
also
![]() $T_{\mathcal{F}}$
-split. Consider following diagram
$T_{\mathcal{F}}$
-split. Consider following diagram

Note that first square is pushout diagram. From 3.11,
![]() $\nabla (\alpha \oplus \alpha ')$
is
$\nabla (\alpha \oplus \alpha ')$
is
![]() $T_{\mathcal{F}}$
-split. Now consider the diagram
$T_{\mathcal{F}}$
-split. Now consider the diagram

Here, second square is pullback diagram. Now from 3.12,
![]() $\alpha + \alpha =(\nabla (\alpha \oplus \alpha '))\Delta$
is
$\alpha + \alpha =(\nabla (\alpha \oplus \alpha '))\Delta$
is
![]() $T_{\mathcal{F}}$
-split.
$T_{\mathcal{F}}$
-split.
We now show
Theorem 4.2.
(with hypotheses as in
4.1
)
![]() ${T_{\mathcal{F}}} \colon{\mathrm{CM}}(-) \times{\mathrm{CM}}(-) \rightarrow \mathrm{mod}(A)$
is a functor.
${T_{\mathcal{F}}} \colon{\mathrm{CM}}(-) \times{\mathrm{CM}}(-) \rightarrow \mathrm{mod}(A)$
is a functor.
Proof. This is similar to [Reference Puthenpurakal20, 3.13]. We have to use Theorem4.1 and Lemmas 3.11, 3.12.
Remark 4.3. Theorems 4.1 and 4.2 also follows directly from the Lemma 3.6 and [Reference Dao, Dey and Dutta8, Theorem 4.8, Proposition 3.8]. Also see [Reference Dao, Dey and Dutta8, Theorem 4.17]. However, for the sake of completion, we have given a proof of these theorems.
Note that the proof of [Reference Dao, Dey and Dutta8, Theorem 4.8] also works for any totally ordered abelian group in place of
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
The following is one of the main results of our paper.
Theorem 4.4.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d$
with uncountable residue field. Let
$d$
with uncountable residue field. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F}=\{{I_n}\}$
where
$\mathcal{F}=\{{I_n}\}$
where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n= \overline{I^{n}}$
for
$I_n= \overline{I^{n}}$
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $M, N$
be MCM
$M, N$
be MCM
![]() $A$
-module then
$A$
-module then
![]() $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
$\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
Proof.
We prove this theorem by induction. If
![]() $\dim A=1$
, then
$\dim A=1$
, then
![]() $\mathrm{Ext}^1_A(M,N)$
has finite length. In fact, for any prime ideal
$\mathrm{Ext}^1_A(M,N)$
has finite length. In fact, for any prime ideal
![]() $\mathfrak{p}\ne \mathfrak{m}$
,
$\mathfrak{p}\ne \mathfrak{m}$
,
![]() $(\mathrm{Ext}^1_A(M,N))_{\mathfrak{p}}=0$
because
$(\mathrm{Ext}^1_A(M,N))_{\mathfrak{p}}=0$
because
![]() $A$
is reduced. Note that for dimension one case, we do not need any assumption on residue field.
$A$
is reduced. Note that for dimension one case, we do not need any assumption on residue field.
We now assume
![]() $\dim A \geq 2$
and result is true for dimension
$\dim A \geq 2$
and result is true for dimension
![]() $d-1$
.
$d-1$
.
Let
![]() $\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0\in \mathrm{Ext}^1_A(M,N)$
and
$\alpha \;:\; 0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0\in \mathrm{Ext}^1_A(M,N)$
and
![]() $a\in I$
. Then we have following pushout diagram of
$a\in I$
. Then we have following pushout diagram of
![]() $R$
-modules for all
$R$
-modules for all
![]() $n\geq 1$
$n\geq 1$

Set
![]() $\mathcal{V} = \{ M, N, E, E_n \colon n \geq 1 \}$
and set
$\mathcal{V} = \{ M, N, E, E_n \colon n \geq 1 \}$
and set
We now do the base change as described in 3.3.II.(iii):
For any MCM
![]() $A$
-module
$A$
-module
![]() $L$
, set
$L$
, set
![]() $L_B = L\otimes _{A}B$
.
$L_B = L\otimes _{A}B$
.
Let
![]() $\mathcal{F}_B = \{ I_nB \}_{n \in \mathbb{Z}}$
. From 3.3.II.(iii), for all
$\mathcal{F}_B = \{ I_nB \}_{n \in \mathbb{Z}}$
. From 3.3.II.(iii), for all
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\zeta$
is
$\zeta$
is
![]() $\mathcal{F}_B$
-superficial for
$\mathcal{F}_B$
-superficial for
Set
![]() $C = B/\zeta B$
,
$C = B/\zeta B$
,
![]() $\mathcal{F}_C = \{ I_nC \}_{n \in \mathbb{Z}}$
. Then
$\mathcal{F}_C = \{ I_nC \}_{n \in \mathbb{Z}}$
. Then
![]() $C$
is analytically unramified with
$C$
is analytically unramified with
![]() $\dim C = d -1$
. Furthermore,
$\dim C = d -1$
. Furthermore,
![]() $I_1C = \overline{I_1C}$
and
$I_1C = \overline{I_1C}$
and
![]() $I_nC = \overline{I^nC}$
for
$I_nC = \overline{I^nC}$
for
![]() $n \gg 0$
. From 3.5, we have for all
$n \gg 0$
. From 3.5, we have for all
![]() $n \geq 0$
,
$n \geq 0$
,
But from the assumption result is true for
![]() $C$
. So
$C$
. So
This implies
![]() $e^T_{\mathcal{F},A}(a^n\alpha )=0$
for
$e^T_{\mathcal{F},A}(a^n\alpha )=0$
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $I=(a_1,\ldots, a_u)$
. It follows that
$I=(a_1,\ldots, a_u)$
. It follows that
So
![]() $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
$\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
Theorem 4.5.
Let
![]() $(A,\mathfrak{m})$
be a Cohen–Macaulay analytically unramified local ring of dimension
$(A,\mathfrak{m})$
be a Cohen–Macaulay analytically unramified local ring of dimension
![]() $d$
with residue field
$d$
with residue field
![]() $k$
. Suppose
$k$
. Suppose
![]() $k$
is perfect field. Let
$k$
is perfect field. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F}=\{{I_n}\}$
where
$\mathcal{F}=\{{I_n}\}$
where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n= \overline{I^{n}}$
for
$I_n= \overline{I^{n}}$
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $M, N$
be MCM
$M, N$
be MCM
![]() $A$
-module and then
$A$
-module and then
![]() $\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
$\mathrm{Ext}_A^1(M,N)/T_{\mathcal{F}}(M,N)$
has finite length.
Proof.
By 3.3, we may assume
![]() $A$
is complete. If
$A$
is complete. If
![]() $k$
is uncountable, the result follows from Theorem4.4.
$k$
is uncountable, the result follows from Theorem4.4.
Now we consider the case when
![]() $k$
is finite or countably infinite. Then by 3.3(iv), there exists a flat local extension
$k$
is finite or countably infinite. Then by 3.3(iv), there exists a flat local extension
![]() $(B,\mathfrak{n})$
of
$(B,\mathfrak{n})$
of
![]() $A$
with
$A$
with
![]() $({\mathfrak{m}} B = \mathfrak{n}$
which behaves well with respect to integral closure such that the residue field of
$({\mathfrak{m}} B = \mathfrak{n}$
which behaves well with respect to integral closure such that the residue field of
![]() $B$
is uncountable. Set
$B$
is uncountable. Set
![]() $\mathcal{F}_B=\{{I_nB}\}_{n \in \mathbb{Z}}$
,
$\mathcal{F}_B=\{{I_nB}\}_{n \in \mathbb{Z}}$
,
![]() $M_B=M\otimes B$
, and
$M_B=M\otimes B$
, and
![]() $N_B=N\otimes B$
. Also note that
$N_B=N\otimes B$
. Also note that
![]() ${I_n}B=\overline{I^nB}$
for
${I_n}B=\overline{I^nB}$
for
![]() $n\gg 0$
.
$n\gg 0$
.
Let
![]() $\alpha \in$
Ext
$\alpha \in$
Ext
![]() $^1_A(M,N)$
and
$^1_A(M,N)$
and
![]() $a\in \mathfrak{m}$
. Then for all
$a\in \mathfrak{m}$
. Then for all
![]() $n\geq 1$
, it is easy to see
$n\geq 1$
, it is easy to see
From Theorem4.4,
![]() $e^T_{\mathcal{F}_B}((a^n\otimes 1)(\alpha \otimes B))=0$
for
$e^T_{\mathcal{F}_B}((a^n\otimes 1)(\alpha \otimes B))=0$
for
![]() $n\gg 0$
. So,
$n\gg 0$
. So,
![]() $e^T_{\mathcal{F}}(a^n\alpha )=0$
for
$e^T_{\mathcal{F}}(a^n\alpha )=0$
for
![]() $n\gg 0$
. Therefore,
$n\gg 0$
. Therefore,
![]() $a^n\alpha \in T_{\mathcal{F}}(M,N)$
for
$a^n\alpha \in T_{\mathcal{F}}(M,N)$
for
![]() $n\gg 0$
. Now the result follows from the similar argument as in Theorem4.4.
$n\gg 0$
. Now the result follows from the similar argument as in Theorem4.4.
5. Weak Brauer–Thrall-II
We need the following two results.
Lemma 5.1.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
. Let
$d\geq 1$
. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F}=\{{I_n}\}$
where
$\mathcal{F}=\{{I_n}\}$
where
![]() $I_1=\overline{I}$
and
$I_1=\overline{I}$
and
![]() $I_n= \overline{I^{n}}$
for
$I_n= \overline{I^{n}}$
for
![]() $n\gg 0$
. If
$n\gg 0$
. If
![]() $M,N$
and
$M,N$
and
![]() $E$
are MCM modules, thenwe have a
$E$
are MCM modules, thenwe have a
![]() $T_{\mathcal{F}}$
-split sequence
$T_{\mathcal{F}}$
-split sequence
![]() $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
. Assume
$0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
. Assume
![]() $G_{\mathcal{F}}(N)$
is Cohen–Macaulay. Then we have short exact sequence
$G_{\mathcal{F}}(N)$
is Cohen–Macaulay. Then we have short exact sequence
Furthermore,
![]() $e_i^{\mathcal{F}}(E)= e_i^{\mathcal{F}}(N)+e_i^{\mathcal{F}}(M)$
for
$e_i^{\mathcal{F}}(E)= e_i^{\mathcal{F}}(N)+e_i^{\mathcal{F}}(M)$
for
![]() $i=0,\ldots, d$
.
$i=0,\ldots, d$
.
Proof. Follows from an argument similar to [Reference Puthenpurakal20, Lemma 6.3].
Proposition 5.2.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal, and
$\mathfrak{m}$
-primary ideal, and
![]() $\mathcal{F}=\{\overline{I^n}\}_{n\geq 0}$
. Assume the residue field
$\mathcal{F}=\{\overline{I^n}\}_{n\geq 0}$
. Assume the residue field
![]() $k = A/{\mathfrak{m}}$
is either uncountable or a perfect field. Let
$k = A/{\mathfrak{m}}$
is either uncountable or a perfect field. Let
![]() $M$
and
$M$
and
![]() $N$
be MCM
$N$
be MCM
![]() $A$
-modules with
$A$
-modules with
![]() $G_{\mathcal{F}}(M)$
and
$G_{\mathcal{F}}(M)$
and
![]() $G_{\mathcal{F}}(N)$
Cohen–Macaulay. If there exists only finitely many non-isomorphic MCM
$G_{\mathcal{F}}(N)$
Cohen–Macaulay. If there exists only finitely many non-isomorphic MCM
![]() $A$
-modules
$A$
-modules
![]() $E$
with
$E$
with
![]() $G_{\mathcal{F}}(E)$
Cohen–Macaulay and
$G_{\mathcal{F}}(E)$
Cohen–Macaulay and
![]() $e^{\mathcal{F}}(E)= e^{\mathcal{F}}(N)+e^{\mathcal{F}}(M)$
, then
$e^{\mathcal{F}}(E)= e^{\mathcal{F}}(N)+e^{\mathcal{F}}(M)$
, then
![]() $T_{\mathcal{F}}(M,N)$
has finite length (in particular Ext
$T_{\mathcal{F}}(M,N)$
has finite length (in particular Ext
![]() $^1_A(M,N)$
has finite length).
$^1_A(M,N)$
has finite length).
Proof. Follows from an argument similar to [Reference Puthenpurakal20, Theorem 7.1].
The following result is well known. We indicate a proof for the convenience of the reader.
Lemma 5.3.
Let
![]() $(A,\mathfrak{m})$
be a Noetherian local ring and
$(A,\mathfrak{m})$
be a Noetherian local ring and
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $A$
. Set
$A$
. Set
![]() $B=A[X]$
and
$B=A[X]$
and
![]() $J=(I,X)$
, then
$J=(I,X)$
, then
![]() $\overline{J^n}=\sum _{i=0}^{n} \overline{I^{n-i}}X^i$
.
$\overline{J^n}=\sum _{i=0}^{n} \overline{I^{n-i}}X^i$
.
Proof.
Consider Rees algebra of
![]() $I$
,
$I$
,
![]() $\mathscr{R}(I)= A[It] = A\oplus It\oplus I^2t^2\oplus \ldots$
. Its integral closure in
$\mathscr{R}(I)= A[It] = A\oplus It\oplus I^2t^2\oplus \ldots$
. Its integral closure in
![]() $A[t]$
is
$A[t]$
is
![]() $\overline{\mathscr{R}(I)}= A\oplus \overline{I}t\oplus \overline{I^2}t^2\oplus \ldots$
. By [Reference Atiyah and Macdonald2, Chapter 5, Exercise 9], we get that
$\overline{\mathscr{R}(I)}= A\oplus \overline{I}t\oplus \overline{I^2}t^2\oplus \ldots$
. By [Reference Atiyah and Macdonald2, Chapter 5, Exercise 9], we get that
![]() $\overline{\mathscr{R}(I)}[X]$
is integral closure of
$\overline{\mathscr{R}(I)}[X]$
is integral closure of
![]() ${\mathscr{R}(I)}[X]$
in
${\mathscr{R}(I)}[X]$
in
![]() $A[t][X]$
. Comparing homogeneous components for all
$A[t][X]$
. Comparing homogeneous components for all
![]() $n$
, we get
$n$
, we get
![]() $\overline{(I,X)^n}=\sum _{i=0}^{n}\overline{I^{n-i}}X^i$
.
$\overline{(I,X)^n}=\sum _{i=0}^{n}\overline{I^{n-i}}X^i$
.
Proposition 5.4.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension one and
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension one and
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal. Set
$\mathfrak{m}$
-primary ideal. Set
![]() $R=A[X]_{(\mathfrak{m},X)}$
,
$R=A[X]_{(\mathfrak{m},X)}$
,
![]() $J=(I,X)$
,
$J=(I,X)$
,
![]() $\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$
, and
$\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$
, and
![]() $\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$
. Then there exists an MCM
$\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$
. Then there exists an MCM
![]() $R$
-module
$R$
-module
![]() $E$
with
$E$
with
![]() $G_{\mathcal{J}}(E)$
Cohen–Macaulay and dim Ext
$G_{\mathcal{J}}(E)$
Cohen–Macaulay and dim Ext
![]() $^1_R(E,E)\gt 0$
.
$^1_R(E,E)\gt 0$
.
Proof.
Let
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module. Fix large enough
$A$
-module. Fix large enough
![]() $n$
(say
$n$
(say
![]() $n_0$
), then it is easy to see
$n_0$
), then it is easy to see
![]() $N=\overline{I^{n_0}}M$
is MCM and
$N=\overline{I^{n_0}}M$
is MCM and
![]() $G_{\mathcal{I}}(N)$
is Cohen–Macaulay. From Lemma 5.3, we get
$G_{\mathcal{I}}(N)$
is Cohen–Macaulay. From Lemma 5.3, we get
![]() $G_{\mathcal{J}}(N\otimes R)= G_{\mathcal{I}}(N)[X]$
. So,
$G_{\mathcal{J}}(N\otimes R)= G_{\mathcal{I}}(N)[X]$
. So,
![]() $G_{\mathcal{J}}(N\otimes R)$
is Cohen–Macaulay.
$G_{\mathcal{J}}(N\otimes R)$
is Cohen–Macaulay.
From [Reference Bruns and Herzog4, Theorem A.11(b)], dim Ext
![]() $^1_R(N\otimes R, N\otimes R) \gt 0$
.
$^1_R(N\otimes R, N\otimes R) \gt 0$
.
Theorem 5.5.
Let
![]() $(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be an analytically unramified Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal. Set
$\mathfrak{m}$
-primary ideal. Set
![]() $R=A[X_1,\ldots, X_m]_{(\mathfrak{m},X_1,\ldots, X_m)}$
,
$R=A[X_1,\ldots, X_m]_{(\mathfrak{m},X_1,\ldots, X_m)}$
,
![]() $J=(I,X_1,\ldots, X_m)$
,
$J=(I,X_1,\ldots, X_m)$
,
![]() $\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$
, and
$\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$
, and
![]() $\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$
. Also set
$\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$
. Also set
![]() $S = \widehat{R}$
and
$S = \widehat{R}$
and
![]() $\mathcal{K}=\{\overline{J^n}S\}_{n\geq 0}$
. If
$\mathcal{K}=\{\overline{J^n}S\}_{n\geq 0}$
. If
![]() $A$
has an MCM module
$A$
has an MCM module
![]() $M$
with
$M$
with
![]() $G_{\mathcal{I}}(M)$
Cohen–Macaulay, then
$G_{\mathcal{I}}(M)$
Cohen–Macaulay, then
-
(1)
 $M\otimes R$
is an MCM
$M\otimes R$
is an MCM
 $R$
-module with
$R$
-module with
 $G_{\mathcal{J}}(M\otimes R)$
Cohen–Macaulay and
$G_{\mathcal{J}}(M\otimes R)$
Cohen–Macaulay and
 $\dim \mathrm{Ext}^1_R(M\otimes R,M\otimes R)\gt 0$
.
$\dim \mathrm{Ext}^1_R(M\otimes R,M\otimes R)\gt 0$
. -
(2) We have
 $\overline{J^nS} = \overline{J^n}S$
for all
$\overline{J^nS} = \overline{J^n}S$
for all
 $n \geq 1$
. Furthermore,
$n \geq 1$
. Furthermore,
 $M\otimes S$
is an MCM
$M\otimes S$
is an MCM
 $S$
-module with
$S$
-module with
 $G_{\mathcal{K}}(M\otimes S)$
Cohen–Macaulay and
$G_{\mathcal{K}}(M\otimes S)$
Cohen–Macaulay and
 $\dim \mathrm{Ext}^1_S(M\otimes S,M\otimes S)\gt 0$
.
$\dim \mathrm{Ext}^1_S(M\otimes S,M\otimes S)\gt 0$
.
Proof.
(1) It is sufficient to prove the result for
![]() $n=1$
. So, we can assume
$n=1$
. So, we can assume
![]() $R=A[X]$
. It is easy to see
$R=A[X]$
. It is easy to see
![]() $M\otimes R$
is MCM
$M\otimes R$
is MCM
![]() $R$
-module and
$R$
-module and
![]() $G_{\mathcal{J}}(M\otimes R)=G_{\mathcal{I}}(M)[X]$
(follows from Lemma 5.3). So,
$G_{\mathcal{J}}(M\otimes R)=G_{\mathcal{I}}(M)[X]$
(follows from Lemma 5.3). So,
![]() $G_{\mathcal{J}}(M\otimes R)$
is Cohen–Macaulay.
$G_{\mathcal{J}}(M\otimes R)$
is Cohen–Macaulay.
From [Reference Bruns and Herzog4, Theorem A.11(b)], dim Ext
![]() $^1_R(M\otimes R, M\otimes R) \gt 0$
.
$^1_R(M\otimes R, M\otimes R) \gt 0$
.
(2) The assertion
![]() $\overline{J^nS} = \overline{J^n}S$
for all
$\overline{J^nS} = \overline{J^n}S$
for all
![]() $n \geq 1$
follows from [Reference Huneke and Swanson12, 9.1.1]. For the rest observe that
$n \geq 1$
follows from [Reference Huneke and Swanson12, 9.1.1]. For the rest observe that
![]() $M\otimes _A S = (M \otimes _A R)\otimes _R S$
. This gives
$M\otimes _A S = (M \otimes _A R)\otimes _R S$
. This gives
![]() $\dim \mathrm{Ext}^1_S(M\otimes S,M\otimes S)\gt 0$
. Furthermore,
$\dim \mathrm{Ext}^1_S(M\otimes S,M\otimes S)\gt 0$
. Furthermore,
![]() $G_{\mathcal{K}}(S)$
is a flat extension of
$G_{\mathcal{K}}(S)$
is a flat extension of
![]() $G_{\mathcal{J}}(R)$
with zero-dimensional fiber. Notice
$G_{\mathcal{J}}(R)$
with zero-dimensional fiber. Notice
By Theorem [Reference Matsumura14, 23.3], the result follows.
Theorem 5.6.
Let
![]() $(A,\mathfrak{m})$
be a complete reduced Cohen–Macaulay local ring of dimension
$(A,\mathfrak{m})$
be a complete reduced Cohen–Macaulay local ring of dimension
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $I$
an
$I$
an
![]() $\mathfrak{m}$
-primary ideal. Assume the residue field
$\mathfrak{m}$
-primary ideal. Assume the residue field
![]() $k = A/{\mathfrak{m}}$
is either uncountable or perfect. Set
$k = A/{\mathfrak{m}}$
is either uncountable or perfect. Set
![]() $R=A[[X_1,\ldots, X_m]]$
,
$R=A[[X_1,\ldots, X_m]]$
,
![]() $J=(I,X_1,\ldots, X_m)$
,
$J=(I,X_1,\ldots, X_m)$
,
![]() $\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$
, and
$\mathcal{I}=\{\overline{I^n}\}_{n\geq 0}$
, and
![]() $\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$
. If
$\mathcal{J}=\{\overline{J^n}\}_{n\geq 0}$
. If
![]() $A$
has an MCM module
$A$
has an MCM module
![]() $M$
with
$M$
with
![]() $G_{\mathcal{I}}(M)$
Cohen–Macaulay, then
$G_{\mathcal{I}}(M)$
Cohen–Macaulay, then
![]() $R$
has infinitely many non-isomorphic MCM modules
$R$
has infinitely many non-isomorphic MCM modules
![]() $D$
with
$D$
with
![]() $G_{\mathcal{J}}(D)$
Cohen–Macaulay and bounded multiplicity.
$G_{\mathcal{J}}(D)$
Cohen–Macaulay and bounded multiplicity.
Proof. Follows from 5.1, 5.2, and 5.5.
6. Some results about
 $e^T_A()$
$e^T_A()$
In this section, we prove Theorem1.15 (see Theorem6.3).
Lemma 6.1. Let
![]() $(A,\mathfrak{m}, k)$
be a Cohen–Macaulay local ring and
$(A,\mathfrak{m}, k)$
be a Cohen–Macaulay local ring and
![]() $M,N$
be MCM
$M,N$
be MCM
![]() $A$
-modules. Let
$A$
-modules. Let
![]() $\alpha$
be
$\alpha$
be
![]() $T$
-split and
$T$
-split and
![]() $\alpha '$
be any extension and then
$\alpha '$
be any extension and then
![]() $e^T_A(\alpha +\alpha ')\leq e^T_A(\alpha ')$
. Also, if char
$e^T_A(\alpha +\alpha ')\leq e^T_A(\alpha ')$
. Also, if char
![]() $(A)=p^n\gt 0$
, then
$(A)=p^n\gt 0$
, then
![]() $e^T(\alpha +\alpha ')=e^T_A(\alpha ')$
.
$e^T(\alpha +\alpha ')=e^T_A(\alpha ')$
.
Proof.
Let
![]() $\alpha$
can be represented as
$\alpha$
can be represented as
![]() $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
and
$0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
and
![]() $\alpha '$
as
$\alpha '$
as
![]() $0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$
. Consider following pullback diagram
$0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$
. Consider following pullback diagram

From 3.12,
![]() $\beta$
is
$\beta$
is
![]() $T$
-split. So,
$T$
-split. So,
![]() ${e_{A}^T}(E'')={e_{A}^T}(N)+{e_{A}^T}(E')$
.
${e_{A}^T}(E'')={e_{A}^T}(N)+{e_{A}^T}(E')$
.
Now
![]() $\alpha +\alpha '$
can be written as
$\alpha +\alpha '$
can be written as
![]() $0\rightarrow N\rightarrow Y\rightarrow M\rightarrow 0$
where
$0\rightarrow N\rightarrow Y\rightarrow M\rightarrow 0$
where
![]() $Y=E''/S$
and
$Y=E''/S$
and
![]() $S=\{(-n,n)\in E''| n\in N\}$
. So, we have following commutative diagram
$S=\{(-n,n)\in E''| n\in N\}$
. So, we have following commutative diagram

Here,
![]() $\delta$
is natural surjection.
$\delta$
is natural surjection.
Now from the exact sequence
![]() $\gamma \;:\; 0\rightarrow N\rightarrow E''\xrightarrow{\delta } Y\rightarrow 0$
, we get
$\gamma \;:\; 0\rightarrow N\rightarrow E''\xrightarrow{\delta } Y\rightarrow 0$
, we get
![]() ${e_{A}^T}(\gamma )={e_{A}^T}(N)+{e_{A}^T}(Y)-{e_{A}^T}(E'')$
.
${e_{A}^T}(\gamma )={e_{A}^T}(N)+{e_{A}^T}(Y)-{e_{A}^T}(E'')$
.
Now we get
 \begin{align*} e^T_A(\alpha +\alpha ')&=e^T_A(N)+{e_{A}^T}(M)-{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ')+{e_{A}^T}(E') -{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ')+{e_{A}^T}(E'')-{e_{A}^T}(N)-{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ') -{e_{A}^T}(\gamma ) \end{align*}
\begin{align*} e^T_A(\alpha +\alpha ')&=e^T_A(N)+{e_{A}^T}(M)-{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ')+{e_{A}^T}(E') -{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ')+{e_{A}^T}(E'')-{e_{A}^T}(N)-{e_{A}^T}(Y)\\ &={e_{A}^T}(\alpha ') -{e_{A}^T}(\gamma ) \end{align*}
So,
![]() $e^T_A(\alpha +\alpha ')\leq{e_{A}^T}(\alpha ').$
$e^T_A(\alpha +\alpha ')\leq{e_{A}^T}(\alpha ').$
If char
![]() $(A)=p^n \gt 0$
, then we have
$(A)=p^n \gt 0$
, then we have
Note that
![]() $p^n\alpha =0$
is split exact sequence.
$p^n\alpha =0$
is split exact sequence.
This implies
![]() $e^T_A(\alpha +\alpha ')={e_{A}^T}(\alpha ').$
$e^T_A(\alpha +\alpha ')={e_{A}^T}(\alpha ').$
Let
![]() $\mathbb{N}$
be the set of non-negative integers.
$\mathbb{N}$
be the set of non-negative integers.
Remark 6.2. If
![]() $char(A) = p^n \gt 0$
, then we have a well defined function
$char(A) = p^n \gt 0$
, then we have a well defined function
![]() $[e^T_A] \colon \mathrm{Ext}^1_A(M, N)/T_A(M, N) \rightarrow \mathbb{N}$
.
$[e^T_A] \colon \mathrm{Ext}^1_A(M, N)/T_A(M, N) \rightarrow \mathbb{N}$
.
If
![]() $V$
is a vector space over a field
$V$
is a vector space over a field
![]() $k$
, then let
$k$
, then let
![]() $\mathbb{P}(V)$
denote the projective space determined by
$\mathbb{P}(V)$
denote the projective space determined by
![]() $V$
.
$V$
.
Theorem 6.3.
(with hypotheses as in 6.1) Further assume
![]() $A$
is of characteristic
$A$
is of characteristic
![]() $p \gt 0$
and that
$p \gt 0$
and that
![]() $A$
contains a field
$A$
contains a field
![]() $k \cong A/{\mathfrak{m}}$
. If
$k \cong A/{\mathfrak{m}}$
. If
![]() $\mathrm{Ext}_A^1(M, N) \neq T_A(M,N)$
, then the function
$\mathrm{Ext}_A^1(M, N) \neq T_A(M,N)$
, then the function
![]() $[e^T_A]$
defined in 6.2 factors as:
$[e^T_A]$
defined in 6.2 factors as:
Proof.
Let
![]() $\alpha \in \mathrm{Ext}^1_A(M,N)$
be represented as
$\alpha \in \mathrm{Ext}^1_A(M,N)$
be represented as
![]() $0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
. Let
$0\rightarrow N\rightarrow E\rightarrow M\rightarrow 0$
. Let
![]() $r \in k^*$
and
$r \in k^*$
and
![]() $r\alpha$
be represented as
$r\alpha$
be represented as
![]() $0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$
. Consider the diagram
$0\rightarrow N\rightarrow E'\rightarrow M\rightarrow 0$
. Consider the diagram

Note
![]() $\psi \colon E \rightarrow E'$
is an isomorphism. It follows that
$\psi \colon E \rightarrow E'$
is an isomorphism. It follows that
![]() $e^T(\alpha ) = e^T(r\alpha )$
. The result follows.
$e^T(\alpha ) = e^T(r\alpha )$
. The result follows.
Remark 6.4. All the results in this section are also true for
![]() ${e_{\mathcal{F}}^T}()$
. The same proofs work in that case also.
${e_{\mathcal{F}}^T}()$
. The same proofs work in that case also.
Theorem 6.5. For the rest of this section, we consider the following setup:
![]() $(A,{\mathfrak{m}})$
is a complete reduced CM local ring. Also assume
$(A,{\mathfrak{m}})$
is a complete reduced CM local ring. Also assume
![]() $A$
contains a field
$A$
contains a field
![]() $k \cong A/{\mathfrak{m}}$
. Furthermore,
$k \cong A/{\mathfrak{m}}$
. Furthermore,
![]() $k$
is either uncountable or a perfect field. Let
$k$
is either uncountable or a perfect field. Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F} = \{ I_n \}_{n \in \mathbb{Z}}$
be an
$\mathcal{F} = \{ I_n \}_{n \in \mathbb{Z}}$
be an
![]() $I$
-admissible filtration with
$I$
-admissible filtration with
![]() $I_1 = \overline{I}$
and
$I_1 = \overline{I}$
and
![]() $I_n = \overline{I^n}$
for
$I_n = \overline{I^n}$
for
![]() $n \gg 0$
. Let
$n \gg 0$
. Let
![]() $M, N$
be MCM
$M, N$
be MCM
![]() $A$
-modules and consider the function:
$A$
-modules and consider the function:
Notice
![]() $e^T_{\mathcal{F}}(\alpha ) \leq e^T_{\mathcal{F}}(M) + e^T_{\mathcal{F}}(N)$
. So,
$e^T_{\mathcal{F}}(\alpha ) \leq e^T_{\mathcal{F}}(M) + e^T_{\mathcal{F}}(N)$
. So,
![]() $e^T_{\mathcal{F}}(\mathrm{Ext}_A^1(M,N))$
is a bounded set.
$e^T_{\mathcal{F}}(\mathrm{Ext}_A^1(M,N))$
is a bounded set.
If
![]() $Z$
is a finite set, then set
$Z$
is a finite set, then set
![]() $|Z|$
denote its cardinality.
$|Z|$
denote its cardinality.
Set
![]() $Z_{\mathcal{F}}(M, N) = | e^T_{\mathcal{F}}(\mathrm{Ext}_A^1(M,N))|$
.
$Z_{\mathcal{F}}(M, N) = | e^T_{\mathcal{F}}(\mathrm{Ext}_A^1(M,N))|$
.
Corollary 6.6.
(with hypotheses as in 6.5). Further assume
![]() $k$
is a finite field and
$k$
is a finite field and
![]() $\mathrm{Ext}^1_A(M, N)$
is nonzero and has finite length as an
$\mathrm{Ext}^1_A(M, N)$
is nonzero and has finite length as an
![]() $A$
-module (and so a finite dimensional
$A$
-module (and so a finite dimensional
![]() $k$
-vector space). Set
$k$
-vector space). Set
![]() $c(M, N) = | \mathbb{P}(\mathrm{Ext}_A^1(M, N))|$
. Let
$c(M, N) = | \mathbb{P}(\mathrm{Ext}_A^1(M, N))|$
. Let
![]() $I$
be any
$I$
be any
![]() $\mathfrak{m}$
-primary ideal and
$\mathfrak{m}$
-primary ideal and
![]() $\mathcal{F} = \{ I_n \}_{n \in \mathbb{Z}}$
be an
$\mathcal{F} = \{ I_n \}_{n \in \mathbb{Z}}$
be an
![]() $I$
-admissible filtration with
$I$
-admissible filtration with
![]() $I_1 = \overline{I}$
and
$I_1 = \overline{I}$
and
![]() $I_n = \overline{I^n}$
for
$I_n = \overline{I^n}$
for
![]() $n \gg 0$
. Then
$n \gg 0$
. Then
![]() $Z_{\mathcal{F}}(M, N) \leq c(M, N)$
.
$Z_{\mathcal{F}}(M, N) \leq c(M, N)$
.
Proof.
We may assume
![]() $T_{\mathcal{F}}(M, N) \neq \mathrm{Ext}^1_A(M, N)$
. By 6.3, we get that
$T_{\mathcal{F}}(M, N) \neq \mathrm{Ext}^1_A(M, N)$
. By 6.3, we get that
Note
![]() $| \mathbb{P}(\mathrm{Ext}^1_A(M, N)/T_{\mathcal{F}}(M, N)) |$
is bounded above by
$| \mathbb{P}(\mathrm{Ext}^1_A(M, N)/T_{\mathcal{F}}(M, N)) |$
is bounded above by
![]() $c(M,N)$
. The result follows.
$c(M,N)$
. The result follows.
7. T-split sequences and AR-sequences
The goal of this section is to prove the following result:
Theorem 7.1.
Let
![]() $(A,{\mathfrak{m}})$
be a Henselian Cohen–Macaulay local ring and
$(A,{\mathfrak{m}})$
be a Henselian Cohen–Macaulay local ring and
![]() $M$
be an indecomposable MCM
$M$
be an indecomposable MCM
![]() $A$
-module free on the punctured spectrum of
$A$
-module free on the punctured spectrum of
![]() $M$
. The following assertions are equivalent:
$M$
. The following assertions are equivalent:
-
1. There exists a
 $T$
-split sequence
$T$
-split sequence
 $\alpha \colon 0 \rightarrow K \rightarrow E \rightarrow M \rightarrow 0$
with
$\alpha \colon 0 \rightarrow K \rightarrow E \rightarrow M \rightarrow 0$
with
 $\alpha$
non-split.
$\alpha$
non-split.
-
2. There exists a
 $T$
-split sequence
$T$
-split sequence
 $\beta \colon 0 \rightarrow V \rightarrow U \rightarrow M \rightarrow 0$
with
$\beta \colon 0 \rightarrow V \rightarrow U \rightarrow M \rightarrow 0$
with
 $V$
indecomposable and
$V$
indecomposable and
 $\beta$
non-split.
$\beta$
non-split.
-
3. The AR-sequence ending at
 $M$
is
$M$
is
 $T$
-split.
$T$
-split.
For definition of AR sequences, see [Reference Yoshino23, Chapter 2]. From [Reference Yoshino23, Theorem 3.4], we know that for an indecomposable MCM module over
![]() $A$
, and then there is an AR-sequence ending in
$A$
, and then there is an AR-sequence ending in
![]() $M$
if and only if
$M$
if and only if
![]() $M_{\mathfrak{p}}$
is free for all
$M_{\mathfrak{p}}$
is free for all
![]() $\mathfrak{p}\in$
Spec
$\mathfrak{p}\in$
Spec
![]() $^0(A)=$
Spec
$^0(A)=$
Spec
![]() $(A)\setminus \{\mathfrak{m}\}$
$(A)\setminus \{\mathfrak{m}\}$
Before proving Theorem7.1, we need the following well-known result. We give a proof for the convenience of the reader.
Lemma 7.2.
Let
![]() $A$
be a Noetherian ring and
$A$
be a Noetherian ring and
![]() $N,M$
, and
$N,M$
, and
![]() $E$
are finite
$E$
are finite
![]() $A$
-module. Let
$A$
-module. Let
![]() $N=N_1\oplus N_2$
, and we have following diagram
$N=N_1\oplus N_2$
, and we have following diagram

for
![]() $i=1,2$
. Here,
$i=1,2$
. Here,
![]() $p_i \;:\; N\rightarrow N_i$
is projection map for
$p_i \;:\; N\rightarrow N_i$
is projection map for
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $s$
is non-split, then one of the
$s$
is non-split, then one of the
![]() $s_i$
is non-split.
$s_i$
is non-split.
Proof.
Let
![]() $s_1$
and
$s_1$
and
![]() $s_2$
are split exact sequences. So, we have
$s_2$
are split exact sequences. So, we have
![]() $g_i\;:\; M_i\rightarrow N_i$
for
$g_i\;:\; M_i\rightarrow N_i$
for
![]() $i=1,2$
such that
$i=1,2$
such that
![]() $g_if_i=1_{N_i}$
. Consider function
$g_if_i=1_{N_i}$
. Consider function
![]() $g= (g_1\gamma _1, g_2\gamma _2)\;:\; M\rightarrow N_1\oplus N_2$
. Let
$g= (g_1\gamma _1, g_2\gamma _2)\;:\; M\rightarrow N_1\oplus N_2$
. Let
![]() $(n_1,n_2)\in N$
and then
$(n_1,n_2)\in N$
and then
 \begin{align*} gf(n_1,n_2)&=(g_1\gamma _1f(n_1,n_2), g_2\gamma _2f(n_1,n_2))\\ &=(g_1f_1p_1(n_1,n_2),g_2f_2p_2(n_1,n_2))\\ &=(n_1,n_2) \end{align*}
\begin{align*} gf(n_1,n_2)&=(g_1\gamma _1f(n_1,n_2), g_2\gamma _2f(n_1,n_2))\\ &=(g_1f_1p_1(n_1,n_2),g_2f_2p_2(n_1,n_2))\\ &=(n_1,n_2) \end{align*}
This implies
![]() $g$
is a left inverse of
$g$
is a left inverse of
![]() $f$
, so
$f$
, so
![]() $s$
is split exact sequence.
$s$
is split exact sequence.
We now give
Proof of Theorem
7.1. The assertions (iii)
![]() $\implies$
(ii)
$\implies$
(ii)
![]() $\implies$
(i) are clear.
$\implies$
(i) are clear.
(i)
![]() $\implies$
(ii). As
$\implies$
(ii). As
![]() $A$
is Henselian, the module
$A$
is Henselian, the module
![]() $K$
splits as a sum of indecomposable modules
$K$
splits as a sum of indecomposable modules
![]() $K = K_1\oplus K_2 \oplus \cdots \oplus K_r$
. The result follows from Lemma 7.2.
$K = K_1\oplus K_2 \oplus \cdots \oplus K_r$
. The result follows from Lemma 7.2.
(ii)
![]() $\implies$
(iii). Let
$\implies$
(iii). Let
![]() $\beta \;:\; 0\rightarrow V \rightarrow U\rightarrow M\rightarrow 0$
be
$\beta \;:\; 0\rightarrow V \rightarrow U\rightarrow M\rightarrow 0$
be
![]() $T$
-split and
$T$
-split and
![]() $\beta$
non-split. As
$\beta$
non-split. As
![]() $V$
is indecomposable, we have following diagram
$V$
is indecomposable, we have following diagram

Here,
![]() $s$
is an AR-sequence ending in
$s$
is an AR-sequence ending in
![]() $M$
, see [Reference Yoshino23, 2.3, 2.8]. This implies
$M$
, see [Reference Yoshino23, 2.3, 2.8]. This implies
![]() $s$
is
$s$
is
![]() $T$
-split (see [Reference Puthenpurakal20, Proposition 3.8]).
$T$
-split (see [Reference Puthenpurakal20, Proposition 3.8]).
Remark 7.3. Regarding Proof of Theorem7.1.
![]() $(ii) \Rightarrow (iii)$
: The first square is a pushout diagram [Reference Bühler6, Proposition 2.12.
$(ii) \Rightarrow (iii)$
: The first square is a pushout diagram [Reference Bühler6, Proposition 2.12.
![]() $(i) \Leftrightarrow (iv)$
]. Now since we know
$(i) \Leftrightarrow (iv)$
]. Now since we know
![]() $T$
is a sub-functor of
$T$
is a sub-functor of
![]() $\mathrm{Ext}$
coming from an exact substructure of mod
$\mathrm{Ext}$
coming from an exact substructure of mod
![]() $A$
, [Reference Dao, Dey and Dutta8, Theorem 4.8, Proposition 3.8], then the AR-sequence is in
$A$
, [Reference Dao, Dey and Dutta8, Theorem 4.8, Proposition 3.8], then the AR-sequence is in
![]() $T_A(M,N)$
from definition of Exact structure.
$T_A(M,N)$
from definition of Exact structure.
8. Some observation about complete intersection
In this section, we prove Theorem1.5 (see Theorem8.3).
Theorem 8.1.
Let
![]() $(A,\mathfrak{m})$
be Noetherian local ring and
$(A,\mathfrak{m})$
be Noetherian local ring and
![]() $M$
a finite
$M$
a finite
![]() $A$
-module. We denote the
$A$
-module. We denote the
![]() $n$
-th Betti number of
$n$
-th Betti number of
![]() $A$
module
$A$
module
![]() $M$
as
$M$
as
![]() $\beta ^A_n(M)$
. Then complexity of
$\beta ^A_n(M)$
. Then complexity of
![]() $M$
can be defined as:
$M$
can be defined as:
Theorem 8.2.
Let
![]() $Q$
be a Noetherian ring and
$Q$
be a Noetherian ring and
![]() $f=f_1,\ldots, f_c$
be a
$f=f_1,\ldots, f_c$
be a
![]() $Q$
-regular sequence. Set
$Q$
-regular sequence. Set
![]() $A=Q/(f_1,\ldots, f_c)$
. Let
$A=Q/(f_1,\ldots, f_c)$
. Let
![]() $M$
be a finite
$M$
be a finite
![]() $A$
-module. Note projdim
$A$
-module. Note projdim
![]() $_QM\lt \infty$
.
$_QM\lt \infty$
.
Let
![]() $\mathbb{F}$
is a free resolution of
$\mathbb{F}$
is a free resolution of
![]() $M$
as an
$M$
as an
![]() $A$
-module. Let
$A$
-module. Let
![]() $t_1,\ldots, t_c:\mathbb{F}(+2)\rightarrow \mathbb{F}$
be the Eisenbud operators (see [Reference Eisenbud10, Section 1]). Consider the polynomial ring
$t_1,\ldots, t_c:\mathbb{F}(+2)\rightarrow \mathbb{F}$
be the Eisenbud operators (see [Reference Eisenbud10, Section 1]). Consider the polynomial ring
![]() $B=A[t_1,\ldots, t_c]$
with deg
$B=A[t_1,\ldots, t_c]$
with deg
![]() $(t_i)=2$
for
$(t_i)=2$
for
![]() $i=1,\ldots, c.$
Let
$i=1,\ldots, c.$
Let
![]() $L$
be an
$L$
be an
![]() $A$
-module, and then we can think of Tor
$A$
-module, and then we can think of Tor
![]() $_*^A(M,L)=\bigoplus _{i\geq 0}\text{Tor}^A_i(M,L)$
as a
$_*^A(M,L)=\bigoplus _{i\geq 0}\text{Tor}^A_i(M,L)$
as a
![]() $B$
-module (here we give degree
$B$
-module (here we give degree
![]() $-i$
for an element of Tor
$-i$
for an element of Tor
![]() $_i^A(M,L)$
).
$_i^A(M,L)$
).
Theorem 8.3.
Let
![]() $(Q,\mathfrak{n},k)$
be a Henselian regular local ring and
$(Q,\mathfrak{n},k)$
be a Henselian regular local ring and
![]() $\underline{f} = f_1,\ldots, f_c\in \mathfrak{n}^2$
a regular sequence. Assume
$\underline{f} = f_1,\ldots, f_c\in \mathfrak{n}^2$
a regular sequence. Assume
![]() $k$
is infinite. Set
$k$
is infinite. Set
![]() $I=(f_1,\ldots, f_c)$
and
$I=(f_1,\ldots, f_c)$
and
![]() $(A,\mathfrak{m})= (Q/I,\mathfrak{n}/I)$
. Assume
$(A,\mathfrak{m})= (Q/I,\mathfrak{n}/I)$
. Assume
![]() $\dim A = 1$
. Let
$\dim A = 1$
. Let
![]() $M$
be an indecomposable MCM
$M$
be an indecomposable MCM
![]() $A$
-module with
$A$
-module with
![]() $\mathrm{cx}_AM\ge 2$
and
$\mathrm{cx}_AM\ge 2$
and
be the minimal free resolution of
![]() $M$
. Set
$M$
. Set
![]() $M_r= \mathrm{Syz}_r^A(M)$
. Then there exists
$M_r= \mathrm{Syz}_r^A(M)$
. Then there exists
![]() $r_0$
such that for all
$r_0$
such that for all
![]() $r\geq r_0$
, there are exact sequences
$r\geq r_0$
, there are exact sequences
![]() $ \alpha _r \colon 0\rightarrow K_r\rightarrow M_{r+2}\rightarrow M_r\rightarrow 0$
such that
$ \alpha _r \colon 0\rightarrow K_r\rightarrow M_{r+2}\rightarrow M_r\rightarrow 0$
such that
-
(1)
 $\mathrm{cx} K_r \leq \mathrm{cx} M - 1$
for
$\mathrm{cx} K_r \leq \mathrm{cx} M - 1$
for
 $r \geq r_0$
.
$r \geq r_0$
. -
(2)
 $\alpha _r$
is non-split for
$\alpha _r$
is non-split for
 $r \geq r_0$
.
$r \geq r_0$
. -
(3)
 $\alpha _r$
is
$\alpha _r$
is
 $T$
-split for
$T$
-split for
 $r \geq r_0$
$r \geq r_0$
If furthermore
![]() $M$
is free on the punctured spectrum of
$M$
is free on the punctured spectrum of
![]() $A$
, then the AR-sequence ending at
$A$
, then the AR-sequence ending at
![]() $M_r$
is
$M_r$
is
![]() $T$
-split for all
$T$
-split for all
![]() $r \geq r_0$
.
$r \geq r_0$
.
Proof.
Let
![]() $x$
be an
$x$
be an
![]() $A$
-superficial element. The map
$A$
-superficial element. The map
![]() $\alpha _n \colon A/{\mathfrak{m}^{n}}\rightarrow A/{\mathfrak{m}^{n+1}}$
defined by
$\alpha _n \colon A/{\mathfrak{m}^{n}}\rightarrow A/{\mathfrak{m}^{n+1}}$
defined by
![]() $\alpha (a+\mathfrak{m}^n) = ax+\mathfrak{m}^{n+1}$
induces an isomorphism of
$\alpha (a+\mathfrak{m}^n) = ax+\mathfrak{m}^{n+1}$
induces an isomorphism of
![]() ${\mathrm{Tor}}^A_i(A/\mathfrak{m}^n,M)$
and
${\mathrm{Tor}}^A_i(A/\mathfrak{m}^n,M)$
and
![]() ${\mathrm{Tor}}^A_i(A/\mathfrak{m}^{n+1},M)$
for
${\mathrm{Tor}}^A_i(A/\mathfrak{m}^{n+1},M)$
for
![]() $n \geq \mathrm{red}(A)$
(see [Reference Puthenpurakal18, Lemma 4.1(3)]).
$n \geq \mathrm{red}(A)$
(see [Reference Puthenpurakal18, Lemma 4.1(3)]).
Fix
![]() $n_0\geq \mathrm{red}(A)$
. For
$n_0\geq \mathrm{red}(A)$
. For
![]() $j = 1,\ldots, n_0$
, we have
$j = 1,\ldots, n_0$
, we have
![]() ${\mathrm{Tor}}_*^A(A/\mathfrak{m}^{j},M)= \bigoplus _{i\geq 0}{\mathrm{Tor}}_i^A(A/\mathfrak{m}^{j},M)$
is *-Artinian
${\mathrm{Tor}}_*^A(A/\mathfrak{m}^{j},M)= \bigoplus _{i\geq 0}{\mathrm{Tor}}_i^A(A/\mathfrak{m}^{j},M)$
is *-Artinian
![]() $B=A[t_1,\ldots, t_c]$
module, where
$B=A[t_1,\ldots, t_c]$
module, where
![]() $t_1,\ldots, t_c$
are Eisenbud operators. Then for
$t_1,\ldots, t_c$
are Eisenbud operators. Then for
![]() $i\gg 0$
(say
$i\gg 0$
(say
![]() $i \geq i_0$
) and for
$i \geq i_0$
) and for
![]() $j = 1, \ldots, n_0$
, we have following exact sequence:
$j = 1, \ldots, n_0$
, we have following exact sequence:
Here,
![]() $\xi$
is a linear combination of
$\xi$
is a linear combination of
![]() $t_1, \ldots, t_c$
(see [Reference Eisenbud10, Lemma 3.3]).
$t_1, \ldots, t_c$
(see [Reference Eisenbud10, Lemma 3.3]).
We have following commutative diagram for
![]() $i\geq i_0$
$i\geq i_0$

where
![]() $\theta _i ={\mathrm{Tor}}^A_i(\alpha _{n_0}, M)$
. As
$\theta _i ={\mathrm{Tor}}^A_i(\alpha _{n_0}, M)$
. As
![]() $\theta _i$
and
$\theta _i$
and
![]() $\theta _{i+2}$
are isomorphisms, we get that the bottom row is also surjective. Iterating we get an exact sequence for all
$\theta _{i+2}$
are isomorphisms, we get that the bottom row is also surjective. Iterating we get an exact sequence for all
![]() $j \geq 1$
and for all
$j \geq 1$
and for all
![]() $i \geq i_0$
,
$i \geq i_0$
,
Note
![]() $\xi$
induces a chain map
$\xi$
induces a chain map
![]() $\xi \colon \mathbb{F}[2] \rightarrow \mathbb{F}$
. As we have a surjection
$\xi \colon \mathbb{F}[2] \rightarrow \mathbb{F}$
. As we have a surjection
by Nakayama Lemma we have surjections
![]() $F_{i+2} \xrightarrow{\xi } F_i$
for all
$F_{i+2} \xrightarrow{\xi } F_i$
for all
![]() $i \geq i_0$
(say with kernel
$i \geq i_0$
(say with kernel
![]() $G_i$
). Notice we have a short exact sequence of complexes:
$G_i$
). Notice we have a short exact sequence of complexes:
Thus, we have surjections
![]() $M_{i+2} \xrightarrow{\xi } M_i$
for all
$M_{i+2} \xrightarrow{\xi } M_i$
for all
![]() $i \geq i_0$
, say with kernel
$i \geq i_0$
, say with kernel
![]() $K_i$
. We note that
$K_i$
. We note that
![]() $ \mathbb{G}_{\geq i_0}$
is a free resolution of
$ \mathbb{G}_{\geq i_0}$
is a free resolution of
![]() $K_{i_0}$
and that
$K_{i_0}$
and that
![]() $K_i$
is (possibly upto a free summand) the
$K_i$
is (possibly upto a free summand) the
![]() $(i-i_0)^{th}$
syzygy of
$(i-i_0)^{th}$
syzygy of
![]() $K_{i_0}$
. It follows that
$K_{i_0}$
. It follows that
![]() $\mathrm{cx} K_{i} = \mathrm{cx} K_{i_0} \leq \mathrm{cx} M -1$
. We have an exact sequence
$\mathrm{cx} K_{i} = \mathrm{cx} K_{i_0} \leq \mathrm{cx} M -1$
. We have an exact sequence
![]() $\alpha _r \colon 0 \rightarrow K_r \rightarrow M_{r+2} \rightarrow M_r \rightarrow 0$
for all
$\alpha _r \colon 0 \rightarrow K_r \rightarrow M_{r+2} \rightarrow M_r \rightarrow 0$
for all
![]() $r \geq r_0$
. Since
$r \geq r_0$
. Since
![]() $M$
is indecomposable,
$M$
is indecomposable,
![]() $M_r = \mathrm{Syz}_r^A(M)$
is also indecomposable for all
$M_r = \mathrm{Syz}_r^A(M)$
is also indecomposable for all
![]() $r \geq 1$
(see [Reference Yoshino23, Lemma 8.17]). As
$r \geq 1$
(see [Reference Yoshino23, Lemma 8.17]). As
![]() $\mathrm{cx} M \geq 2$
it follows that
$\mathrm{cx} M \geq 2$
it follows that
![]() $M_{r+2} \ncong M_r$
for all
$M_{r+2} \ncong M_r$
for all
![]() $r \geq 1$
. It follows that
$r \geq 1$
. It follows that
![]() $\alpha _r$
is not split for all
$\alpha _r$
is not split for all
![]() $r \geq r_0$
.
$r \geq r_0$
.
By 8.2 it follows that for
![]() $i \geq i_0$
, we have an exact seqquence
$i \geq i_0$
, we have an exact seqquence
for all
![]() $j \geq 1$
. Clearly, this implies that
$j \geq 1$
. Clearly, this implies that
![]() $\alpha _i$
is
$\alpha _i$
is
![]() $T$
-split.
$T$
-split.
Notice
![]() $M_r$
is free on Spec
$M_r$
is free on Spec
![]() $^0(A)$
for all
$^0(A)$
for all
![]() $r \geq 1$
. As
$r \geq 1$
. As
![]() $\alpha _r$
is
$\alpha _r$
is
![]() $T$
-split, it follows from 7.1 that the AR-sequence ending at
$T$
-split, it follows from 7.1 that the AR-sequence ending at
![]() $M_r$
is
$M_r$
is
![]() $T$
-split for all
$T$
-split for all
![]() $r \geq r_0$
.
$r \geq r_0$
.
9.
 $T$
-split sequences on hypersurfaces defined by quadrics
$T$
-split sequences on hypersurfaces defined by quadrics
In this section, we prove Theorem1.6 (see Theorem9.4). We also construct Example 1.7 (see 9.5).
Theorem 9.1.
In this section,
![]() $(Q,\mathfrak{n})$
is a Henselian regular local ring with algebraically closed residue field
$(Q,\mathfrak{n})$
is a Henselian regular local ring with algebraically closed residue field
![]() $k = Q/\mathfrak{n}$
and let
$k = Q/\mathfrak{n}$
and let
![]() $f \in \mathfrak{n}^2 \setminus \mathfrak{n}^3$
. Assume the hypersurface
$f \in \mathfrak{n}^2 \setminus \mathfrak{n}^3$
. Assume the hypersurface
![]() $A = Q/(f)$
is an isolated singularity of dimension
$A = Q/(f)$
is an isolated singularity of dimension
![]() $d \geq 1$
.
$d \geq 1$
.
Remark 9.2. Here, we are taking the definition of an Ulrich module as a maximal Cohen–Macaulay module with
![]() $e_0(M)=\mu (M)$
(see also [Reference Brennan, Herzog and Ulrich3]).
$e_0(M)=\mu (M)$
(see also [Reference Brennan, Herzog and Ulrich3]).
It is well known that as
![]() $f$
is a quadric, the ring
$f$
is a quadric, the ring
![]() $A$
has minimal multiplicity. It follows that
$A$
has minimal multiplicity. It follows that
![]() $e_0(A) = 2$
and
$e_0(A) = 2$
and
![]() $e_1(A) = 1$
. We also have that if
$e_1(A) = 1$
. We also have that if
![]() $M$
is MCM, then
$M$
is MCM, then
![]() $N = \mathrm{Syz}^A_1(M)$
is Ulrich, that is,
$N = \mathrm{Syz}^A_1(M)$
is Ulrich, that is,
![]() $\mu (N) = e_0(N)$
(furthermore,
$\mu (N) = e_0(N)$
(furthermore,
![]() $e_1(N) =0)$
. As
$e_1(N) =0)$
. As
![]() $A$
is also Gorenstein, we get that any MCM
$A$
is also Gorenstein, we get that any MCM
![]() $A$
-module
$A$
-module
![]() $M \cong F \oplus E$
where
$M \cong F \oplus E$
where
![]() $F$
is free and
$F$
is free and
![]() $E$
has no-free summands and is a syzygy of an MCM
$E$
has no-free summands and is a syzygy of an MCM
![]() $A$
-module; in particular,
$A$
-module; in particular,
![]() $E$
is Ulrich.
$E$
is Ulrich.
The following results compute
![]() $e^T(-)$
for MCM
$e^T(-)$
for MCM
![]() $A$
-modules. We also give a sufficient condition for a short exact sequence to be
$A$
-modules. We also give a sufficient condition for a short exact sequence to be
![]() $T$
-split.
$T$
-split.
Proposition 9.3.
(with hypotheses as in 9.1) Let
![]() $M, N, U, V$
be MCM
$M, N, U, V$
be MCM
![]() $A$
-modules with
$A$
-modules with
![]() $M, N$
having no free summands. Then
$M, N$
having no free summands. Then
-
(1)
 $e^T(M) = \mu (M)$
.
$e^T(M) = \mu (M)$
. -
(2) Let
 $U = L \oplus F$
where
$U = L \oplus F$
where
 $F$
is free and
$F$
is free and
 $L$
has no free summands. Then
$L$
has no free summands. Then
 $e^T(U) = \mu (L)$
.
$e^T(U) = \mu (L)$
. -
(3) Let
 $\alpha \colon 0 \rightarrow N \rightarrow V \rightarrow M \rightarrow 0$
. If
$\alpha \colon 0 \rightarrow N \rightarrow V \rightarrow M \rightarrow 0$
. If
 $\mu (V) = \mu (N) + \mu (M)$
then
$\mu (V) = \mu (N) + \mu (M)$
then
-
(a)
 $V$
is Ulrich
$V$
is Ulrich
-
(b)
 $\alpha$
is
$\alpha$
is
 $T$
-split.
$T$
-split.
-
Proof.
(1) Note
![]() $\mathrm{Syz}^A_1(M)$
is also Ulrich. Using 9.2, we have
$\mathrm{Syz}^A_1(M)$
is also Ulrich. Using 9.2, we have
(2) Note
![]() $e^T(U) = e^T(L) + e^T(F) = \mu (L) + 0 = \mu (L)$
.
$e^T(U) = e^T(L) + e^T(F) = \mu (L) + 0 = \mu (L)$
.
(3) We have
 \begin{align*} e_0(V) &= e_0(M) + e_0(N), \\ &= \mu (M) + \mu (N) \quad \text{as $M, N$ are Ulrich,} \\ &= \mu (V). \end{align*}
\begin{align*} e_0(V) &= e_0(M) + e_0(N), \\ &= \mu (M) + \mu (N) \quad \text{as $M, N$ are Ulrich,} \\ &= \mu (V). \end{align*}
In particular,
![]() $V$
is Ulrich. Note that, this also follows from [Reference Dao, Dey and Dutta8, Lemma 5.2.2]. So,
$V$
is Ulrich. Note that, this also follows from [Reference Dao, Dey and Dutta8, Lemma 5.2.2]. So,
![]() $V$
has no free summands. We have
$V$
has no free summands. We have
So,
![]() $\alpha$
is
$\alpha$
is
![]() $T$
-split.
$T$
-split.
We now state and prove the main result of this section.
Theorem 9.4.
(with hypotheses as in 9.1) All but a finitely many AR-sequences of
![]() $A$
are
$A$
are
![]() $T$
-split.
$T$
-split.
Proof.
We may assume that
![]() $A$
is of infinite CM representation type (i.e., there exists infinitely many mutually non-isomorphic indecomposable MCM
$A$
is of infinite CM representation type (i.e., there exists infinitely many mutually non-isomorphic indecomposable MCM
![]() $A$
-modules); otherwise, there is nothing to prove. The AR-quiver of
$A$
-modules); otherwise, there is nothing to prove. The AR-quiver of
![]() $A$
is locally finite graph, [Reference Yoshino23, 5.9]. It follows that for all but finitely many MCM indecomposable
$A$
is locally finite graph, [Reference Yoshino23, 5.9]. It follows that for all but finitely many MCM indecomposable
![]() $A$
-modules, the middle term of the AR-sequence ending at
$A$
-modules, the middle term of the AR-sequence ending at
![]() $M$
and
$M$
and
![]() $\mathrm{Syz}^A_1(M)$
will not contain a free summand. Let
$\mathrm{Syz}^A_1(M)$
will not contain a free summand. Let
![]() $M$
be such a indecomposable MCM
$M$
be such a indecomposable MCM
![]() $A$
-module and let
$A$
-module and let
![]() $s \colon 0 \rightarrow \tau (M) \rightarrow V \rightarrow M \rightarrow 0$
be the AR-sequence ending at
$s \colon 0 \rightarrow \tau (M) \rightarrow V \rightarrow M \rightarrow 0$
be the AR-sequence ending at
![]() $M$
. Then by [Reference Puthenpurakal19, 7.11], we have
$M$
. Then by [Reference Puthenpurakal19, 7.11], we have
![]() $\mu (V) = \mu (M) + \mu (\tau (M))$
. Note that the hypotheses of [Reference Puthenpurakal19, 7.11] are satisfied, especially, there is no irreducible map
$\mu (V) = \mu (M) + \mu (\tau (M))$
. Note that the hypotheses of [Reference Puthenpurakal19, 7.11] are satisfied, especially, there is no irreducible map
![]() $A \rightarrow M$
because
$A \rightarrow M$
because
![]() $V$
has no free summand, [Reference Yoshino23, 2.12]. The reason for the absence of the irrudicble map
$V$
has no free summand, [Reference Yoshino23, 2.12]. The reason for the absence of the irrudicble map
![]() $A \rightarrow \mathrm{Syz}^A_1(M)$
due to [Reference Puthenpurakal19, 2.3, 7.4, 7.6]. By 9.3(3), it follows that
$A \rightarrow \mathrm{Syz}^A_1(M)$
due to [Reference Puthenpurakal19, 2.3, 7.4, 7.6]. By 9.3(3), it follows that
![]() $s$
is
$s$
is
![]() $T$
-split.
$T$
-split.
We now give example of an AR-sequence which is not split.
Example 9.5.
(with hypotheses as in 9.1) Let
![]() $s \colon 0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$
be an AR-sequence such that
$s \colon 0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$
be an AR-sequence such that
![]() $E$
has a free summand. Then
$E$
has a free summand. Then
-
(1)
 $s$
is NOT
$s$
is NOT
 $T$
-split.
$T$
-split.
-
(2) If
 $t \colon 0 \rightarrow V \rightarrow U \rightarrow M \rightarrow 0$
is any non-split exact sequence of MCM
$t \colon 0 \rightarrow V \rightarrow U \rightarrow M \rightarrow 0$
is any non-split exact sequence of MCM
 $A$
-modules then
$A$
-modules then
 $t$
is NOT
$t$
is NOT
 $T$
-split.
$T$
-split.
Proof.
(1) Note
![]() $\mu (N) \geq \mu (E) - \mu (M)$
. Furthermore, equality cannot hold for otherwise by Proposition 9.3 we will get
$\mu (N) \geq \mu (E) - \mu (M)$
. Furthermore, equality cannot hold for otherwise by Proposition 9.3 we will get
![]() $E$
is Ulrich, a contradiction. Let
$E$
is Ulrich, a contradiction. Let
![]() $E = L \oplus F$
with
$E = L \oplus F$
with
![]() $F \neq 0$
free and
$F \neq 0$
free and
![]() $L$
has no free summands. We note that
$L$
has no free summands. We note that
 \begin{align*} e^T(s) &= e^T(N) + e^T(M) - e^T(E), \\ &= \mu (N) + \mu (M) - \mu (L) \\ &\gt \mu (N) + \mu (M) - \mu (E) \gt 0.\\ \end{align*}
\begin{align*} e^T(s) &= e^T(N) + e^T(M) - e^T(E), \\ &= \mu (N) + \mu (M) - \mu (L) \\ &\gt \mu (N) + \mu (M) - \mu (E) \gt 0.\\ \end{align*}
Thus,
![]() $s$
is NOT
$s$
is NOT
![]() $T$
-split.
$T$
-split.
(2) This follows from Theorem7.1.
10. An application of
 $T$
-split sequences in Gorenstein case
$T$
-split sequences in Gorenstein case
In this section, we prove Proposition 1.9 (see 10.6). We also prove Theorem1.10 (see 10.10 and 10.11).
Theorem 10.1.
Let
![]() $(A,\mathfrak{m})$
be a Gorenstein local ring. Let CM
$(A,\mathfrak{m})$
be a Gorenstein local ring. Let CM
![]() $(A)$
denotes the category of MCM
$(A)$
denotes the category of MCM
![]() $A$
-modules and CM
$A$
-modules and CM
![]() $(A)$
the stable category of CM
$(A)$
the stable category of CM
![]() $(A)$
. Note that objects of CM
$(A)$
. Note that objects of CM
![]() $(A)$
are same as the objects of CM
$(A)$
are same as the objects of CM
![]() $(A)$
and if
$(A)$
and if
![]() $M$
and
$M$
and
![]() $N$
are MCM
$N$
are MCM
![]() $A$
-modules, then
$A$
-modules, then
Theorem 10.2.
(Co-syzygy) Let
![]() $(A,\mathfrak{m})$
be a Gorenstein local ring and
$(A,\mathfrak{m})$
be a Gorenstein local ring and
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module. Let
$A$
-module. Let
![]() $M^*=$
Hom
$M^*=$
Hom
![]() $(M,A)$
, and then
$(M,A)$
, and then
![]() $M^{**}\cong M$
. Suppose
$M^{**}\cong M$
. Suppose
![]() $G\xrightarrow{\epsilon } F\rightarrow M^*\rightarrow 0$
is a minimal presentation of
$G\xrightarrow{\epsilon } F\rightarrow M^*\rightarrow 0$
is a minimal presentation of
![]() $M^*$
. Dualizing this, we get
$M^*$
. Dualizing this, we get
![]() $0\rightarrow M\rightarrow F^*\xrightarrow{\epsilon ^*} G^*$
. Co-syzygy of
$0\rightarrow M\rightarrow F^*\xrightarrow{\epsilon ^*} G^*$
. Co-syzygy of
![]() $M$
can be defined as coker
$M$
can be defined as coker
![]() $(\epsilon ^*)$
and denoted as
$(\epsilon ^*)$
and denoted as
![]() $\Omega ^{-1}(M)$
. So, we have exact sequence
$\Omega ^{-1}(M)$
. So, we have exact sequence
![]() $0\rightarrow M\rightarrow F\rightarrow \Omega ^{-1}(M)\rightarrow 0$
.
$0\rightarrow M\rightarrow F\rightarrow \Omega ^{-1}(M)\rightarrow 0$
.
Note that co-syzygy does not depend on the minimal presentation, that is, if we take another minimal presentation
![]() $G'\xrightarrow{\epsilon '} F'\rightarrow M^*\rightarrow 0$
, then coker
$G'\xrightarrow{\epsilon '} F'\rightarrow M^*\rightarrow 0$
, then coker
![]() $(\epsilon ^*)\cong$
coker
$(\epsilon ^*)\cong$
coker
![]() $((\epsilon ')^*)$
.
$((\epsilon ')^*)$
.
Theorem 10.3.
Let
![]() $\Omega ^{-1}(M)$
be the co-syzygy of
$\Omega ^{-1}(M)$
be the co-syzygy of
![]() $M$
, and then we have following exact sequence:
$M$
, and then we have following exact sequence:
here
![]() $F$
is a free
$F$
is a free
![]() $A$
-module (see 10.2).
$A$
-module (see 10.2).
For any
![]() $f\in \text{{Hom}}_A(M,N)$
, we have following diagram
$f\in \text{{Hom}}_A(M,N)$
, we have following diagram

Here, the first sequare is a pushout diagram.
Remark 10.4. Note that CM
![]() $(A)$
is an triangulated category with the projection of the sequence
$(A)$
is an triangulated category with the projection of the sequence
![]() $M\xrightarrow{f}N\xrightarrow{i} C(f)\xrightarrow{-p} \Omega ^{-1}(M)$
in CM
$M\xrightarrow{f}N\xrightarrow{i} C(f)\xrightarrow{-p} \Omega ^{-1}(M)$
in CM
![]() $(A)$
as a basic triangles for any morphism
$(A)$
as a basic triangles for any morphism
![]() $f$
. Exact triangles are triangles isomorphic to a basic triangle (see [Reference Buchweitz5, 4.7]). Also note that for any short exact sequence
$f$
. Exact triangles are triangles isomorphic to a basic triangle (see [Reference Buchweitz5, 4.7]). Also note that for any short exact sequence
![]() $0\rightarrow U\rightarrow V\rightarrow W\rightarrow 0$
in CM
$0\rightarrow U\rightarrow V\rightarrow W\rightarrow 0$
in CM
![]() $(A)$
, we have exact triangle
$(A)$
, we have exact triangle
![]() $U\rightarrow V\rightarrow W\rightarrow \Omega ^{-1}(U)$
(see [Reference Puthenpurakal17, Remark 3.3]).
$U\rightarrow V\rightarrow W\rightarrow \Omega ^{-1}(U)$
(see [Reference Puthenpurakal17, Remark 3.3]).
Theorem 10.5.
Let
![]() $M$
and
$M$
and
![]() $N$
be MCM
$N$
be MCM
![]() $A$
-modules, and then it is easy to show that
$A$
-modules, and then it is easy to show that
In fact, the map
![]() $\eta \;:\; f\mapsto \alpha _f$
is an isomorphism. It is clear that
$\eta \;:\; f\mapsto \alpha _f$
is an isomorphism. It is clear that
![]() $\eta$
is natural in
$\eta$
is natural in
![]() $M$
and
$M$
and
![]() $N$
.
$N$
.
Let
![]() $T_A(\Omega ^{-1}(M),N)$
denotes the set of all
$T_A(\Omega ^{-1}(M),N)$
denotes the set of all
![]() $T$
-split sequences in Ext
$T$
-split sequences in Ext
![]() $^1_A(\Omega ^{-1}(M),N)$
. If we denote
$^1_A(\Omega ^{-1}(M),N)$
. If we denote
![]() $\eta ^{-1}(T_A(\Omega ^{-1}(M),N))$
by
$\eta ^{-1}(T_A(\Omega ^{-1}(M),N))$
by
![]() $\mathcal{R}(M,N)$
, then
$\mathcal{R}(M,N)$
, then
![]() $\eta$
induces following isomorphism:
$\eta$
induces following isomorphism:
Proposition 10.6.
![]() $\mathcal{R}$
is a relation on
$\mathcal{R}$
is a relation on
![]() $\underline{\mathrm{CM}}(A)$
.
$\underline{\mathrm{CM}}(A)$
.
Proof.
To prove that
![]() $\mathcal{R}$
is a relation on CM
$\mathcal{R}$
is a relation on CM
![]() $(A)$
, we need to show:
$(A)$
, we need to show:
if
![]() $M_1,M,N,N_1\in$
CM
$M_1,M,N,N_1\in$
CM
![]() $(A)$
,
$(A)$
,
![]() $u\in \mathcal{R}(M,N)$
,
$u\in \mathcal{R}(M,N)$
,
![]() $f\in \underline{{\mathrm{Hom}}}_A(M_1,M)$
, and
$f\in \underline{{\mathrm{Hom}}}_A(M_1,M)$
, and
![]() $g\in \underline{{\mathrm{Hom}}}_A(N,N_1)$
, then
$g\in \underline{{\mathrm{Hom}}}_A(N,N_1)$
, then
![]() $u\circ f\in \mathcal{R}(M_1,N)$
and
$u\circ f\in \mathcal{R}(M_1,N)$
and
![]() $g\circ u\in \mathcal{R}(M,N_1)$
.
$g\circ u\in \mathcal{R}(M,N_1)$
.
We first prove
![]() $u\circ f\in \mathcal{R}(M_1,N)$
. We have following diagram of exact traingles
$u\circ f\in \mathcal{R}(M_1,N)$
. We have following diagram of exact traingles

Note that the map
![]() $h$
exists from the property (TR3) (see [Reference Weibel22, Definition 10.2.1]).
$h$
exists from the property (TR3) (see [Reference Weibel22, Definition 10.2.1]).
So we have following diagram of exact sequences

where
![]() $F$
and
$F$
and
![]() $G$
are free
$G$
are free
![]() $A$
-modules. Now since
$A$
-modules. Now since
![]() $u\in \mathcal{R}(M,N)$
, this implies
$u\in \mathcal{R}(M,N)$
, this implies
![]() $\alpha _u$
is
$\alpha _u$
is
![]() $T$
-split. So from [Reference Puthenpurakal20, Proposition 3.9],
$T$
-split. So from [Reference Puthenpurakal20, Proposition 3.9],
![]() $\alpha _{u\circ f}$
is
$\alpha _{u\circ f}$
is
![]() $T$
-split. In other words,
$T$
-split. In other words,
![]() $u\circ f \in \mathcal{R}(M_1,N)$
.
$u\circ f \in \mathcal{R}(M_1,N)$
.
Next, we prove
![]() $g\circ u\in \mathcal{R}(M,N_1)$
. We have following diagram of exact traingles
$g\circ u\in \mathcal{R}(M,N_1)$
. We have following diagram of exact traingles

Note that the property (TR3) (see [Reference Weibel22, Definition 10.2.1]) guarantees the existence of map
![]() $\theta$
.
$\theta$
.
So we have following diagram of exact sequences

where
![]() $F'$
and
$F'$
and
![]() $G'$
are free
$G'$
are free
![]() $A$
-modules. Now since
$A$
-modules. Now since
![]() $u\in \mathcal{R}(M,N)$
, this implies
$u\in \mathcal{R}(M,N)$
, this implies
![]() $\alpha _u$
is
$\alpha _u$
is
![]() $T$
-split. So from [Reference Puthenpurakal20, Proposition 3.8],
$T$
-split. So from [Reference Puthenpurakal20, Proposition 3.8],
![]() $\alpha _{g\circ u}$
is
$\alpha _{g\circ u}$
is
![]() $T$
-split. In other words,
$T$
-split. In other words,
![]() $g\circ u \in \mathcal{R}(M_1,N)$
.
$g\circ u \in \mathcal{R}(M_1,N)$
.
Remark 10.7. To prove
![]() $\alpha _{u\circ f}$
,
$\alpha _{u\circ f}$
,
![]() $\alpha _{g\circ u} \in T_A(M,N)$
, we can use the fact that
$\alpha _{g\circ u} \in T_A(M,N)$
, we can use the fact that
![]() $T$
is a sub-functor of
$T$
is a sub-functor of
![]() $\mathrm{Ext}$
coming from exact substructure of mod
$\mathrm{Ext}$
coming from exact substructure of mod
![]() $A$
(see [Reference Dao, Dey and Dutta8, Theorem 4.8, Proposition 3.8]).
$A$
(see [Reference Dao, Dey and Dutta8, Theorem 4.8, Proposition 3.8]).
Theorem 10.8.
Since
![]() $\mathcal{R}$
is a relation on CM
$\mathcal{R}$
is a relation on CM
![]() $(A)$
, the factor category
$(A)$
, the factor category
![]() $\mathcal{D}_A=$
CM
$\mathcal{D}_A=$
CM
![]() $(A)/\mathcal{R}$
is an additive category. Note that objects of
$(A)/\mathcal{R}$
is an additive category. Note that objects of
![]() $\mathcal{D}_A$
are the same as those of CM
$\mathcal{D}_A$
are the same as those of CM
![]() $(A)$
, and for any
$(A)$
, and for any
![]() $M,N\in$
Obj
$M,N\in$
Obj
![]() $(\mathcal{D}_A)$
, Hom
$(\mathcal{D}_A)$
, Hom
![]() $_{\mathcal{D}_A}(M,N)=\underline{\mathrm{Hom}}_A(M,N)/\mathcal{R}(M,N)$
.
$_{\mathcal{D}_A}(M,N)=\underline{\mathrm{Hom}}_A(M,N)/\mathcal{R}(M,N)$
.
Also note that
![]() $\ell (\text{Hom}_{\mathcal{D}_A}(M,N))\lt \infty$
(see [Reference Puthenpurakal20, Theorem 4.1]).
$\ell (\text{Hom}_{\mathcal{D}_A}(M,N))\lt \infty$
(see [Reference Puthenpurakal20, Theorem 4.1]).
Next, we want to prove the main result of this section. But, first we prove a lemma.
Lemma 10.9.
Let
![]() $(A,\mathfrak{m})$
be a Henselian Gorenstein local ring and
$(A,\mathfrak{m})$
be a Henselian Gorenstein local ring and
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module. Then
$A$
-module. Then
![]() $\mathcal{R}(M,M)\subseteq$
Jac(End
$\mathcal{R}(M,M)\subseteq$
Jac(End
![]() $_A(M))$
in CM
$_A(M))$
in CM
![]() $(A)$
.
$(A)$
.
Proof. We prove this result in three cases:
Case 1:
![]() $M$
is indecomposable MCM module.
$M$
is indecomposable MCM module.
Let
![]() $u\in \mathcal{R}(M,M)$
and if possible assume that
$u\in \mathcal{R}(M,M)$
and if possible assume that
![]() $u\notin$
Jac(End
$u\notin$
Jac(End
![]() $_A(M))$
. This implies
$_A(M))$
. This implies
![]() $u$
is invertible. Now, we have following diagram of exact sequences
$u$
is invertible. Now, we have following diagram of exact sequences

From here, we get
![]() $C(u)\cong F$
. Also from the assumption,
$C(u)\cong F$
. Also from the assumption,
![]() $\alpha _u$
is
$\alpha _u$
is
![]() $T$
-split. We know that
$T$
-split. We know that
![]() $e^T(\alpha _u)=e^T(M)+ e^T(\Omega ^{-1}(M))-e^T(C(u))$
.
$e^T(\alpha _u)=e^T(M)+ e^T(\Omega ^{-1}(M))-e^T(C(u))$
.
So,
![]() $e^T(\alpha _u)=e^T(M)+ e^T(\Omega ^{-1}(M))$
because
$e^T(\alpha _u)=e^T(M)+ e^T(\Omega ^{-1}(M))$
because
![]() $C(u)\cong F$
. This implies
$C(u)\cong F$
. This implies
![]() $e^T(\alpha _u)\gt 0$
, but this is a contradiction because
$e^T(\alpha _u)\gt 0$
, but this is a contradiction because
![]() $\alpha _u$
is
$\alpha _u$
is
![]() $T$
-split. Therefore,
$T$
-split. Therefore,
![]() $u\in$
Jac(End
$u\in$
Jac(End
![]() $_A(M))$
.
$_A(M))$
.
Case 2:
![]() $M\cong E^n$
for some indecomposable MCM module
$M\cong E^n$
for some indecomposable MCM module
![]() $E$
.
$E$
.
It is clear that
![]() $\mathcal{R}(M,M)= \mathcal{R}(E^n,E^n)\cong M_n(\mathcal{R}(E,E))$
. Here,
$\mathcal{R}(M,M)= \mathcal{R}(E^n,E^n)\cong M_n(\mathcal{R}(E,E))$
. Here,
![]() $M_n()$
denotes
$M_n()$
denotes
![]() $n\times n$
-matrix.
$n\times n$
-matrix.
We also know that End
![]() $(E^n)\cong M_n(\underline{\mathrm{End}}(E))$
and
$(E^n)\cong M_n(\underline{\mathrm{End}}(E))$
and
Jac(End
![]() $(E^n))\cong M_n(\text{Jac}(\underline{\mathrm{End}}(E)))$
. From the case (1),
$(E^n))\cong M_n(\text{Jac}(\underline{\mathrm{End}}(E)))$
. From the case (1),
![]() $M_n(\mathcal{R}(E,E))\subseteq M_n(\text{Jac}(\underline{\mathrm{End}}(E)))$
.
$M_n(\mathcal{R}(E,E))\subseteq M_n(\text{Jac}(\underline{\mathrm{End}}(E)))$
.
So,
![]() $\mathcal{R}(M,M)\subseteq \text{Jac}(\underline{\mathrm{End}}(M))$
.
$\mathcal{R}(M,M)\subseteq \text{Jac}(\underline{\mathrm{End}}(M))$
.
Case 3:
![]() $M\cong M_1^{r_1}\oplus \ldots \oplus M_q^{r_q}$
with each
$M\cong M_1^{r_1}\oplus \ldots \oplus M_q^{r_q}$
with each
![]() $M_i$
indecomposable for all
$M_i$
indecomposable for all
![]() $i=1,\ldots, q$
and
$i=1,\ldots, q$
and
![]() $M_i\ncong M_j$
if
$M_i\ncong M_j$
if
![]() $i\ne j$
(since
$i\ne j$
(since
![]() $A$
is complete, KRS holds for CM
$A$
is complete, KRS holds for CM
![]() $(A)$
).
$(A)$
).
We can assume that
![]() $q\gt 1$
because
$q\gt 1$
because
![]() $q=1$
case follows from case (2).
$q=1$
case follows from case (2).
Now it is sufficient to prove the following claim.
Claim: Let
![]() $E$
and
$E$
and
![]() $L$
be MCM
$L$
be MCM
![]() $A$
-module. Assume that
$A$
-module. Assume that
![]() $E\cong E_1^{a_1}\oplus \ldots \oplus E_n^{a_n}$
and
$E\cong E_1^{a_1}\oplus \ldots \oplus E_n^{a_n}$
and
![]() $L\cong L_1^{b_1}\oplus \ldots \oplus L_r^{b_r}$
where
$L\cong L_1^{b_1}\oplus \ldots \oplus L_r^{b_r}$
where
![]() $E_i$
and
$E_i$
and
![]() $L_j$
are distinct indecomposable MCM modules and
$L_j$
are distinct indecomposable MCM modules and
![]() $E_i\ncong L_j$
for
$E_i\ncong L_j$
for
![]() $i=1,\ldots, n$
and
$i=1,\ldots, n$
and
![]() $j=1,\ldots, r$
. If the lemma is true for
$j=1,\ldots, r$
. If the lemma is true for
![]() $E$
and
$E$
and
![]() $L$
, then it is also true for
$L$
, then it is also true for
![]() $N=E\oplus L$
.
$N=E\oplus L$
.
Proof of the claim: We know that
and
Since the result is true for
![]() $E$
and
$E$
and
![]() $L$
, this implies
$L$
, this implies
![]() $\mathcal{R}(N,N)\subseteq \text{Jac}(\underline{\mathrm{End}}_A(N))$
.
$\mathcal{R}(N,N)\subseteq \text{Jac}(\underline{\mathrm{End}}_A(N))$
.
Theorem 10.10.
Let
![]() $(A,\mathfrak{m})$
be a Henselian Gorenstein local ring,
$(A,\mathfrak{m})$
be a Henselian Gorenstein local ring,
![]() $M$
and
$M$
and
![]() $N$
be MCM
$N$
be MCM
![]() $A$
-modules. Then
$A$
-modules. Then
![]() $M\cong N$
in
$M\cong N$
in
![]() $\mathcal{D}_A$
if and only if
$\mathcal{D}_A$
if and only if
![]() $M\cong N$
in CM
$M\cong N$
in CM
![]() $(A)$
.
$(A)$
.
Proof.
Let
![]() $f\;:\;M\rightarrow N$
be an isomorphism in CM
$f\;:\;M\rightarrow N$
be an isomorphism in CM
![]() $(A)$
. Then,
$(A)$
. Then,
![]() $f$
is an isomorphism of
$f$
is an isomorphism of
![]() $M$
and
$M$
and
![]() $N$
in
$N$
in
![]() $\mathcal{D}_A$
.
$\mathcal{D}_A$
.
For the other direction, suppose
![]() $ f\;:\;M\rightarrow N$
be an isomorphism in
$ f\;:\;M\rightarrow N$
be an isomorphism in
![]() $\mathcal{D}_A$
. Then there exists an isomorphism
$\mathcal{D}_A$
. Then there exists an isomorphism
![]() $g\;:\;N\rightarrow M$
such that
$g\;:\;N\rightarrow M$
such that
![]() $g\circ f=\mu$
and
$g\circ f=\mu$
and
![]() $\mu =1 +\delta$
for some
$\mu =1 +\delta$
for some
![]() $\delta \in \mathcal{R}(M,M)$
. From Lemma 10.9,
$\delta \in \mathcal{R}(M,M)$
. From Lemma 10.9,
![]() $\delta \in$
Jac(End
$\delta \in$
Jac(End
![]() $_A(M))$
. This implies
$_A(M))$
. This implies
![]() $\mu$
is an isomorphism in CM
$\mu$
is an isomorphism in CM
![]() $(A)$
. Therefore,
$(A)$
. Therefore,
![]() $g\circ f$
is an isomorphism in CM
$g\circ f$
is an isomorphism in CM
![]() $(A)$
. Similarly,
$(A)$
. Similarly,
![]() $f\circ g$
is also an isomorphism in CM
$f\circ g$
is also an isomorphism in CM
![]() $(A)$
. This implies
$(A)$
. This implies
![]() $M\cong N$
in CM
$M\cong N$
in CM
![]() $(A)$
.
$(A)$
.
Proposition 10.11.
Let
![]() $(A,\mathfrak{m})$
be a Henselian Gorenstein local ring. If
$(A,\mathfrak{m})$
be a Henselian Gorenstein local ring. If
![]() $M$
is indecomposable in
$M$
is indecomposable in
![]() $\underline{\mathrm{CM}}(A)$
, then it is indecomposable in
$\underline{\mathrm{CM}}(A)$
, then it is indecomposable in
![]() $\mathcal{D}_A$
. Furthermore,
$\mathcal{D}_A$
. Furthermore,
![]() $\mathcal{D}_A$
is a (KRS) category.
$\mathcal{D}_A$
is a (KRS) category.
Proof.
Let
![]() $M$
be an MCM
$M$
be an MCM
![]() $A$
-module, and then
$A$
-module, and then
![]() $M\cong M_1^{a_1}\oplus \ldots \oplus M_n^{a_n}$
in
$M\cong M_1^{a_1}\oplus \ldots \oplus M_n^{a_n}$
in
![]() $\underline{\mathrm{CM}}(A)$
; here, each
$\underline{\mathrm{CM}}(A)$
; here, each
![]() $M_i$
is distinct indecomposable non-free MCM
$M_i$
is distinct indecomposable non-free MCM
![]() $A$
-module.
$A$
-module.
For any indecomposable non-free MCM module
![]() $N$
, we know
$N$
, we know
![]() $\underline{\text{End}}_A(N)$
is a local ring and End
$\underline{\text{End}}_A(N)$
is a local ring and End
![]() $_{\mathcal{D}_A}(N)= \underline{\text{End}}_A(N)/\mathcal{R}(N,N)$
. From Lemma 10.9,
$_{\mathcal{D}_A}(N)= \underline{\text{End}}_A(N)/\mathcal{R}(N,N)$
. From Lemma 10.9,
![]() $\mathcal{R}(N,N)\subseteq \text{Jac}(\underline{\mathrm{End}}_A(N))$
. So, End
$\mathcal{R}(N,N)\subseteq \text{Jac}(\underline{\mathrm{End}}_A(N))$
. So, End
![]() $_{\mathcal{D}_A}(N)$
is a local ring. Thus,
$_{\mathcal{D}_A}(N)$
is a local ring. Thus,
![]() $N$
is indecomposable in
$N$
is indecomposable in
![]() $\mathcal{D}_A$
.
$\mathcal{D}_A$
.
Remark 10.12. The statements of the Lemma 10.9, Theorem 10.10, and Proposition 10.11 are valid for any relation
![]() $\mathcal{R}$
coming from a sub-functor of
$\mathcal{R}$
coming from a sub-functor of
![]() $\mathrm{Ext}$
of the exact substructure of mod
$\mathrm{Ext}$
of the exact substructure of mod
![]() $A$
as long as the subadditive function
$A$
as long as the subadditive function
![]() $\phi$
is 0 on free modules ( also see [Reference Dao, Dey and Dutta8, Theorem 4.8]).
$\phi$
is 0 on free modules ( also see [Reference Dao, Dey and Dutta8, Theorem 4.8]).