No CrossRef data available.
Article contents
Quasidistinguished countable enlargements of normed spaces
Published online by Cambridge University Press: 18 May 2009
Extract
If E is a Hausdorff locally convex space and M is an 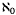 -dimensional subspace of the algebraic dual E* that is transverse to the continuous dual E′, then, according to [7], the Mackey topology τ(E, E′ + M) is a countable enlargement (CE) of τ(E, E′) [or of E]. Much is still unknown as to when CEs preserve barrelledness (cf. [14]). E is quasidistinguished (QD) if each bounded subset of the completion Ê is contained in the completion of a bounded subset of E [12]. Clearly, each normed space is QD, and Tsirulnikov [12] asked if each CE of a normed space must be a QDCE, i.e., must preserve the QD property. Since CEs preserve metrizability (but not normability), her question was whether metrizable spaces so obtained must be QD, and was moderated by Amemiya's negative answer (cf. [5, p. 404]) to Grothendieck's query, who had asked if all metrizable spaces are QD, having proved the separable ones are [4].
-dimensional subspace of the algebraic dual E* that is transverse to the continuous dual E′, then, according to [7], the Mackey topology τ(E, E′ + M) is a countable enlargement (CE) of τ(E, E′) [or of E]. Much is still unknown as to when CEs preserve barrelledness (cf. [14]). E is quasidistinguished (QD) if each bounded subset of the completion Ê is contained in the completion of a bounded subset of E [12]. Clearly, each normed space is QD, and Tsirulnikov [12] asked if each CE of a normed space must be a QDCE, i.e., must preserve the QD property. Since CEs preserve metrizability (but not normability), her question was whether metrizable spaces so obtained must be QD, and was moderated by Amemiya's negative answer (cf. [5, p. 404]) to Grothendieck's query, who had asked if all metrizable spaces are QD, having proved the separable ones are [4].
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1996


