Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T07:22:46.812Z Has data issue: false hasContentIssue false
  • English
  • Français

φ-PRIME SUBMODULES

Published online by Cambridge University Press:  25 November 2009

NASER ZAMANI
NASER ZAMANI*
Affiliation:
Faculty of Science, University of Mohaghegh Ardabili, P.O. Box 179, Ardabil, Iran e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring with non-zero identity and M be a unitary R-module. Let 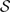(M) be the set of all submodules of M, and φ: 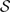(M) → 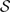(M) ∪ {∅} be a function. We say that a proper submodule P of M is a prime submodule relative to φ or φ-prime submodule if a ∈ R and x ∈ M, with ax ∈ P ∖ φ(P) implies that a ∈(P :RM) or x ∈ P. So if we take φ(N) = ∅ for each N ∈ 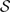(M), then a φ-prime submodule is exactly a prime submodule. Also if we consider φ(N) = {0} for each submodule N of M, then in this case a φ-prime submodule will be called a weak prime submodule. Some of the properties of this concept will be investigated. Some characterisations of φ-prime submodules will be given, and we show that under some assumptions prime submodules and φ1-prime submodules coincide.

Keywords

13C05
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 2 , May 2010 , pp. 253 - 259
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Anderson, D. D. and Bataineh, M., Generalizatins of prime ideals, Comm. Algebra 36 (2008), 686–696.Google Scholar
2.Dauns, J., Prime modules, J. Reine Angew. Math. 298 (1978), 156–181.Google Scholar
3.Lu, C. P., Prime submodules, Comm. Math. Univ. Sancti Pauli 33 (1984), 61–69.Google Scholar
4.McCasland, R. L. and Moore, M. E., Prime submodules, Comm. Algebra 20 (1992), 1803–1817.Google Scholar
5.McCasland, R. L. and Smith, P. F., Prime submodules of Noetherian modules, Rocky Mountain J. Math. 23 (1993), 1041–1062.CrossRefGoogle Scholar
6.Moore, M. E. and Smith, S. J., Prime and radical submodules of modules over commutative rings, Comm. Algebra 30 (2002), 5037–5064.Google Scholar
7.Sharp, R., Steps in commutative algebra (Cambridge University Press, Cambridge, 2000).Google Scholar