No CrossRef data available.
Article contents
Positive matrices and eigenvectors†
Published online by Cambridge University Press: 18 May 2009
Extract
For i, j = 1, 2, …, let aij be real. A matrix A = (aij) will be called positive (A>0) or non-negative (A≧0) according as, for all i and j, aij>0 or aij≧0 respectively. Correspondingly, a real vector x = (x1, x2, …) will be called positive (x>0) or non-negative (x≧0) according as, for all i, xi>0 or x≧0. A matrix A is said to be bounded if ∥ Ax ∥ ≦M ∥ x ∥ holds for some constant M, 0 ≦ M < ∞, and all x in the Hilbert space H of real vectors x = (x1, x2, …) satisfying 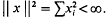 . The least such constant M is denoted by ∥ A ∥. If x and y belong to H, then (x, y) will denote as usual the scalar product Σxiyi. Whether or not x is in H, or A is bounded, y = Ax will be considered as defined by
. The least such constant M is denoted by ∥ A ∥. If x and y belong to H, then (x, y) will denote as usual the scalar product Σxiyi. Whether or not x is in H, or A is bounded, y = Ax will be considered as defined by

whenever each of the series of (1) is convergent.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1963


