Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T03:47:50.201Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SPECTRA OF PISOT NUMBERS

Published online by Cambridge University Press:  09 December 2011

TOUFIK ZAIMI
TOUFIK ZAIMI*
Affiliation:
Département de mathématiques Université Larbi Ben M'hidi Oum El Bouaghi 04000, Algérie e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let θ be a real number greater than 1, and let (()) be the fractional part function. Then, θ is said to be a Z-number if there is a non-zero real number λ such that ((λθn)) < for all n ∈ ℕ. Dubickas (A. Dubickas, Even and odd integral parts of powers of a real number, Glasg. Math. J., 48 (2006), 331–336) showed that strong Pisot numbers are Z-numbers. Here it is proved that θ is a strong Pisot number if and only if there exists λ ≠ 0 such that ((λα)) < for all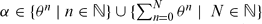. Also, the following characterisation of Pisot numbers among real numbers greater than 1 is shown: θ is a Pisot number ⇔ ∃ λ ≠ 0 such that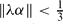for allan ∈ {0,1}, N ∈ ℕ}, where ‖λα‖ = min{((λα)), 1 − ((λα))}.

Keywords

11R8011J7111R06
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 1 , January 2012 , pp. 127 - 132
Copyright
Copyright © Glasgow Mathematical Journal Trust 2011

References

REFERENCES

1.Bertin, M. J., Decomps-Guilloux, A., Grandet-Hugo, M., Pathiaux-Delefosse, M. and Schreiber, J. P., Pisot and Salem numbers (Birkhäuser Verlag Basel, 1992).CrossRefGoogle Scholar
2.Boyd, D. W., Linear recurrence relations for some generalized Pisot sequences, in Advances in Number Theory, Proceedings of the 1991 CNTA Conference (Gouvea, F. Q. and Yui, N., Editors) (Oxford University Press, Oxford, UK, 1993), 333–340.Google Scholar
3.Dubickas, A., Even and odd integral parts of powers of a real number, Glasg. Math. J. 48 (2006), 331–336.CrossRefGoogle Scholar
4.Pisot, C., La répartition modulo un et les nombres algébriques, Annali Scuola Norm. Sup. Pisa. 7 (1938), 205–248.Google Scholar
5.Salem, R., Algebraic numbers and Fourier analysis (Heath Math. Monographs, Health, Boston, MA, 1963).Google Scholar
6.Smyth, C. J., The conjugates of algebraic integers, Amer. Math. Mont. 82 (1975), 86.CrossRefGoogle Scholar
7.Zaïmi, T., Comments on the distribution modulo one of powers of Pisot and Salem numbers, Publ. Math. Debrecen (to appear).Google Scholar