Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-04T19:33:54.527Z Has data issue: false hasContentIssue false
  • English
  • Français

On the representations of numbers by binary cubic forms

Published online by Cambridge University Press:  18 May 2009

C. Hooley
C. Hooley
Affiliation:
Department of Pure Mathematics, University College, Cardiff.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are not a few situations in the theory of numbers where it is desirable to have as sharp an estimate as possible for the number r(n) of representations of a positive integer n by an irreducible binary cubic form

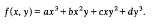
A variety of approaches are available for this problem but, as they stand, they are all defective in that they introduce unwanted factors into the estimate. For instance, an estimate involving the discriminant of f(x, y) is obtained if we adopt the Lagrange procedure [5] of using congruences of the type f(σ, 1)≡0, mod n, to reduce the problem to one where n=1. Alternatively, following Oppenheim (vid. [2]), Greaves [3], and others, we may appeal to the theory of factorization of ideals, which leads to unwanted logarithmic factors owing to the involvement of algebraic units. Having had need, however, in some recent work on quartic forms [4] for an estimate without such extraneous imperfections, we intend in the present note to prove that

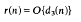
uniformly with respect to the coefficients of f(x, y), where ds(n) denotes the number of ways of expressing n as a product of s factors.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 27 , October 1985 , pp. 95 - 98
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Delone, B. N. and Faddeev, D. K., The theory of irrationalities of the third degree, Translations of Mathematical Monographs, Vol. 10, American Math. Soc. (1964).Google Scholar
2.Evelyn, C. J. A. and Linfoot, E. H., On a problem in the additive theory of numbers, J. reine angew. Math. 164 (1931), 131–140.Google Scholar
3.Greaves, G., On the representation of a number of a sum of two fourth powers, Math. Z. 94 (1966), 233–234.CrossRefGoogle Scholar
4.Hooley, C., On binary quartic forms (to appear).Google Scholar
5.Lagrange, J. L., Nouvelle méthode pour résoudre les problèmes indeterminées en nombres entires, Mémoires de Berlin, 24 (1770).Google Scholar