Hostname: page-component-7bb8b95d7b-nptnm Total loading time: 0 Render date: 2024-09-06T12:33:51.686Z Has data issue: false hasContentIssue false
  • English
  • Français

On the fundamental group of a Lie semigroup

Published online by Cambridge University Press:  18 May 2009

Karl-Hermann Neeb
Karl-Hermann Neeb
Affiliation:
Université Paris VI, Département de Mathématioues, Analyse Complexe et Géometrie, 4, Place Jussieu, 75252 Paris, Cedex 05, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The simplest type of Lie semigroups are closed convex cones in finite dimensional vector spaces. In general one defines a Lie semigroup to be a closed subsemigroup of a Lie group which is generated by one-parameter semigroups. If W is a closed convex cone in a vector space V, then W is convex and therefore simply connected. A similar statement for Lie semigroups is false in general. There exist generating Lie semigroups in simply connected Lie groups which are not simply connected (Example 1.15). To find criteria for cases when this is true, one has to consider the homomorphism

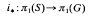
induced by the inclusion mapping i:S→G, where S is a generating Lie semigroup in the Lie group G. Our main results concern the description of the image and the kernel of this mapping. We show that the image is the fundamental group of the largest covering group of G, into which S lifts, and that the kernel is the fundamental group of the inverse image of 5 in the universal covering group G. To get these results we construct a universal covering semigroup S of S. If j: H(S): = S ∩ S-1 →S is the inclusion mapping of the unit group of S into S, then it turns out that the kernel of the induced mapping

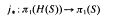
may be identfied with the fundamental group of the unit group H(S)of S and that its image corresponds to the intersection H(S)0 ⋂π1(S), where π1(s) is identified with a central subgroup of S.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 3 , September 1992 , pp. 379 - 394
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, American Math. Soc, Mathematical Surveys No. 7 (Providence, Rhode Island, 1961).Google Scholar
2.Dörr, N., On Ol'shanskii's semigroup, Math. Ann. 288 (1990), 21–33.CrossRefGoogle Scholar
3.Graham, G., Differentiable semigroups, Lecture Notes in Mathematics 998 (1983), 57–127.CrossRefGoogle Scholar
4.Hilgert, J., A note on Howe's oscillator semigroup, Ann. Inst. Fourier (Grenoble) 39 (1990), 663–688.CrossRefGoogle Scholar
5.Hilgert, J., Hofmann, K. H. and Lawson, J. D., Lie groups, convex cones and semigroups (Oxford University Press, 1989).Google Scholar
6.Hofmann, K. H. and Ruppert, W. A. F., On the interior of subsemigroups of Lie groups, Trans. Amer. Math. Soc. 324 (1991), 169–179.CrossRefGoogle Scholar
7.Kahn, H. D., Covering semigroups, Pacific J. Math. 34 (1970), 427–439.CrossRefGoogle Scholar
8.Lawson, J. D., Polar and Ol'shanskii decompositions, Seminar Sophus Lie 1 (1991).Google Scholar
9.Neeb, K.-H., The duality between subsemigroups of Lie groups and monotone functions, Trans. Amer. Math. Soc. 329 (1992), 653–677.CrossRefGoogle Scholar
10.Neeb, K.-H., Conal orders on homogeneous spaces, Invent. Math. 104 (1991), 467–496.CrossRefGoogle Scholar
11.Neeb, K.-H., Invariant orders on Lie groups and coverings of ordered homogeneous spaces, submitted.Google Scholar
12.Ruppert, W. A. F., On open subsemigroups of connected groups, Semigroup Forum 39 (1989), 347–362.CrossRefGoogle Scholar
13.Schubert, H., Topologie (Teubner Verlag, Stuttgart, 1975).Google Scholar
14.Tits, J., Liesche Gruppen und Algebren (Springer, New York, Heidelberg, 1983).CrossRefGoogle Scholar