Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T09:36:25.729Z Has data issue: false hasContentIssue false
  • English
  • Français

ON NONLOCAL NONLINEAR ELLIPTIC PROBLEMS WITH THE FRACTIONAL LAPLACIAN

Part of: Partial differential equations Variational problems in infinite-dimensional spaces Elliptic equations and systems Global differential geometry

Published online by Cambridge University Press:  29 January 2019

LI MA
LI MA*
Affiliation:
School of Mathematics and Physics, University of Science and Technology Beijing, 30 Xueyuan Road, Haidian District, Beijing 100083, China; Department of Mathematics, Henan Normal University, Xinxiang 453007, China e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the existence of positive solutions to a semilinear nonlocal elliptic problem with the fractional α-Laplacian on Rn, 0 < α < n. We show that the problem has infinitely many positive solutions in 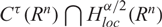$ {C^\tau}({R^n})\bigcap H_{loc}^{\alpha /2}({R^n}) $. Moreover, each of these solutions tends to some positive constant limit at infinity. We can extend our previous result about sub-elliptic problem to the nonlocal problem on Rn. We also show for α ∊ (0, 2) that in some cases, by the use of Hardy’s inequality, there is a nontrivial non-negative 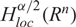$ H_{loc}^{\alpha /2}({R^n}) $ weak solution to the problem

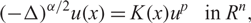$$ {( - \Delta )^{\alpha /2}}u(x) = K(x){u^p} \quad {\rm{ in}} \ {R^n}, $$
where K(x) = K(|x|) is a non-negative non-increasing continuous radial function in Rn and p > 1.

MSC classification

Secondary: 35A15: Variational methods 35B50: Maximum principles 35J60: Nonlinear elliptic equations 53C70: Direct methods ($G$-spaces of Busemann, etc.) 58E50: Applications
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 1 , January 2020 , pp. 75 - 84
Copyright
Copyright © Glasgow Mathematical Journal Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Caffarelli, L. and Silvestre, L., Regularity theory for fully nonlinear integro-differential equations, Comm. Pure Appl. Math. LXXII (2009), 0597–0638.CrossRefGoogle Scholar
Frank, R. L. and Seiringer, R., Non-linear ground state representations and sharp Hardy inequalities, J. Funct. Anal. 255 (2008), 3407–3430.CrossRefGoogle Scholar
Chen, W. and Li, C., Classification of solutions of some nonlinear elliptic equations, Duke Math. J. 63 (1991), 615–622.CrossRefGoogle Scholar
Chen, W., Li, C. and Li, Y., A direct method of moving planes for the fractional Laplacian, Adv. Math. 308 (2017), 404–437. 35R11 (35A01 35B09 35B50).CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L., Symmetry of positive solutions of nonlinear elliptic equations in Rn, in Mathematical Analysis and Applications, Part A (Nachbin, L., Editor), Adv. Math. Suppl. Stud., vol. 7 (Academic Press, New York, 1981), 369–402.Google Scholar
Gidas, B. and Spruck, J., Global and local behavior of positive solutions of nonlinear elliptic equations, Comm. Pure Appl. Math. 34 (1981), 525–598.CrossRefGoogle Scholar
Li, Y. and Ni, W. M., On conformally scalar curvature equations in R n, Duke Math. J. 57 (1988), 895–924.CrossRefGoogle Scholar
Lu, G. and Zhu, J., Symmetry and regularity of extremals of an integral equation related to the Hardy-Sobolev inequality, Calculus Var. Partial Differ Equations 42 (2011), 563–577. doi: 1007/s00526-011-0398-7.CrossRefGoogle Scholar
Ma, L., Boundedness of solutions to Ginzburg–Landau fractional Laplacian equation, Int. J. Math. 27(5) (2016), 1650048.CrossRefGoogle Scholar
Ma, L., Chen, D. and Yang, Y., Some results for subelliptic equations, Acta. Math. Sinica. (English Series) 22 (2006), 1695–1704.CrossRefGoogle Scholar