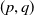1. Introduction
Let
![]() $\Omega \subset \mathbb{R}^n$
,
$\Omega \subset \mathbb{R}^n$
,
![]() $n \,{\geqslant}\, 2$
, be an open, bounded, and connected set and let
$n \,{\geqslant}\, 2$
, be an open, bounded, and connected set and let
![]() $p, q$
be such that
$p, q$
be such that
![]() $1\lt p$
, and
$1\lt p$
, and
![]() $1\lt q\lt p^*$
, where
$1\lt q\lt p^*$
, where
![]() $p^*=np/(n-p)$
if
$p^*=np/(n-p)$
if
![]() $p\lt n$
and
$p\lt n$
and
![]() $p^*=\infty$
if
$p^*=\infty$
if
![]() $p\,{\geqslant}\, n$
. In this paper, we study the following variational problem:
$p\,{\geqslant}\, n$
. In this paper, we study the following variational problem:
 \begin{equation} \lambda ^H_{p,q}(\Omega ) = \inf _{\substack{u\in W^{1,p}_0(\Omega ), \\ u\neq 0}}\frac{\displaystyle \int _\Omega H(\nabla u)^p\,dx}{\bigg (\displaystyle \int _\Omega m|u|^q\,dx\bigg )^{\frac{p}{q}}}, \end{equation}
\begin{equation} \lambda ^H_{p,q}(\Omega ) = \inf _{\substack{u\in W^{1,p}_0(\Omega ), \\ u\neq 0}}\frac{\displaystyle \int _\Omega H(\nabla u)^p\,dx}{\bigg (\displaystyle \int _\Omega m|u|^q\,dx\bigg )^{\frac{p}{q}}}, \end{equation}
where
![]() $m\in L^{\infty }(\Omega )$
is a positive function and
$m\in L^{\infty }(\Omega )$
is a positive function and
![]() $H\;:\;\mathbb R^n\to [0,+\infty]$
is a
$H\;:\;\mathbb R^n\to [0,+\infty]$
is a
![]() $C^1(\mathbb R^n\setminus \{0\})$
convex and positively 1-homogeneous function (see Section 2 for more details).
$C^1(\mathbb R^n\setminus \{0\})$
convex and positively 1-homogeneous function (see Section 2 for more details).
Obviously,
![]() $\lambda ^H_{p,q}(\Omega )$
depends also on
$\lambda ^H_{p,q}(\Omega )$
depends also on
![]() $m$
, but to simplify the notation we will omit its dependence.
$m$
, but to simplify the notation we will omit its dependence.
The Euler–Lagrange equation associated with the minimization problem (1.1) is the following weighted eigenvalue problem for the anisotropic
![]() $(p,q)-$
Laplace operator with Dirichlet boundary condition:
$(p,q)-$
Laplace operator with Dirichlet boundary condition:
 \begin{equation} \begin{cases} -\mathcal{L}_{p}(u)=\lambda m(x)\| u\|_{q,m}^{p-q}|u|^{q-2}u & \mbox{in}\ \Omega \\[5pt] u=0&\mbox{on}\ \partial \Omega, \end{cases} \end{equation}
\begin{equation} \begin{cases} -\mathcal{L}_{p}(u)=\lambda m(x)\| u\|_{q,m}^{p-q}|u|^{q-2}u & \mbox{in}\ \Omega \\[5pt] u=0&\mbox{on}\ \partial \Omega, \end{cases} \end{equation}
where
![]() $\| u\|_{q,m}=\| u\|_{L^q(\Omega, m)}$
is the weighted Lebesgue norm of
$\| u\|_{q,m}=\| u\|_{L^q(\Omega, m)}$
is the weighted Lebesgue norm of
![]() $u$
and
$u$
and
![]() $\mathcal{L}_p$
is the so-called anisotropic
$\mathcal{L}_p$
is the so-called anisotropic
![]() $p$
-Laplacian operator defined as follows:
$p$
-Laplacian operator defined as follows:
We stress that when
![]() $p=q$
and
$p=q$
and
![]() $m(x)\equiv 1$
, (1.1) is the first eigenvalue
$m(x)\equiv 1$
, (1.1) is the first eigenvalue
![]() $\lambda ^H_p(\Omega )$
of the anisotropic
$\lambda ^H_p(\Omega )$
of the anisotropic
![]() $p$
-Laplacian, and it has been studied by many authors (see for instance [Reference Belloni, Ferone and Kawohl9, Reference Della Pietra and Gavitone19] and the references therein). In particular, in [Reference Belloni, Ferone and Kawohl9], it is proved that
$p$
-Laplacian, and it has been studied by many authors (see for instance [Reference Belloni, Ferone and Kawohl9, Reference Della Pietra and Gavitone19] and the references therein). In particular, in [Reference Belloni, Ferone and Kawohl9], it is proved that
![]() $\lambda ^{H}_p(\Omega )$
is simple for any
$\lambda ^{H}_p(\Omega )$
is simple for any
![]() $p$
, the corresponding eigenfunctions have a sign, and that a suitable Faber–Krahn inequality holds.
$p$
, the corresponding eigenfunctions have a sign, and that a suitable Faber–Krahn inequality holds.
When
![]() $H=\mathcal E$
is the usual Euclidean norm,
$H=\mathcal E$
is the usual Euclidean norm,
![]() $ \mathcal{L}_{p}(u)$
is the well-known
$ \mathcal{L}_{p}(u)$
is the well-known
![]() $p$
-Laplace operator and the eigenvalue problem (1.2) reduces to the following:
$p$
-Laplace operator and the eigenvalue problem (1.2) reduces to the following:
 \begin{equation} \begin{cases} -\Delta _p u=\lambda \|u\|_{q,m}^{p-q}|u|^{q-2}u & \mbox{in}\ \Omega \\[5pt] u=0&\mbox{on}\ \partial \Omega . \end{cases} \end{equation}
\begin{equation} \begin{cases} -\Delta _p u=\lambda \|u\|_{q,m}^{p-q}|u|^{q-2}u & \mbox{in}\ \Omega \\[5pt] u=0&\mbox{on}\ \partial \Omega . \end{cases} \end{equation}
The spectrum of (1.4) and the first eigenvalue
![]() $\lambda ^{\mathcal E}_{p,q}(\Omega )$
, when
$\lambda ^{\mathcal E}_{p,q}(\Omega )$
, when
![]() $p\neq q$
and
$p\neq q$
and
![]() $m\equiv 1$
, have been studied for instance in the case
$m\equiv 1$
, have been studied for instance in the case
![]() $p=2$
in [Reference Brasco and Franzina11], for any
$p=2$
in [Reference Brasco and Franzina11], for any
![]() $p$
in [Reference Franzina and Lamberti25, Reference García Azorero and Peral Alonso26, Reference Ôtani34, Reference Ôtani35] and in [Reference Drábek, Kufner and Nicolosi20] where the authors study also the weighted case. It is known that
$p$
in [Reference Franzina and Lamberti25, Reference García Azorero and Peral Alonso26, Reference Ôtani34, Reference Ôtani35] and in [Reference Drábek, Kufner and Nicolosi20] where the authors study also the weighted case. It is known that
![]() $\lambda ^{\mathcal E}_{p,q}(\Omega )$
is not simple, in general, for any
$\lambda ^{\mathcal E}_{p,q}(\Omega )$
is not simple, in general, for any
![]() $1\lt q\lt p^*$
. Indeed in [Reference Idogawa and Ôtani27], the authors prove the simplicity for any
$1\lt q\lt p^*$
. Indeed in [Reference Idogawa and Ôtani27], the authors prove the simplicity for any
![]() $1\lt q\,{\leqslant}\, p$
, while for
$1\lt q\,{\leqslant}\, p$
, while for
![]() $p\lt q\lt p^*$
,
$p\lt q\lt p^*$
,
![]() $\lambda ^{\mathcal E}_{p,q}(\Omega )$
could not be necessary simple. This fact has been observed for instance in [Reference Brasco and Franzina11], in the case
$\lambda ^{\mathcal E}_{p,q}(\Omega )$
could not be necessary simple. This fact has been observed for instance in [Reference Brasco and Franzina11], in the case
![]() $p=2$
, and for any
$p=2$
, and for any
![]() $p$
in [Reference Nazarov32] and [Reference Kawohl, Lucia and Prashanth29], where the authors prove that for every fixed
$p$
in [Reference Nazarov32] and [Reference Kawohl, Lucia and Prashanth29], where the authors prove that for every fixed
![]() $p\lt q\lt p^*$
the simplicity fails if
$p\lt q\lt p^*$
the simplicity fails if
![]() $\Omega$
is a sufficiently thin spherical shell.
$\Omega$
is a sufficiently thin spherical shell.
In this paper, we study the main properties of
![]() $\lambda ^{H}_{p,q}(\Omega )$
and of the corresponding eigenfunctions. In particular, our aim is to prove a reverse Hölder inequality for them.
$\lambda ^{H}_{p,q}(\Omega )$
and of the corresponding eigenfunctions. In particular, our aim is to prove a reverse Hölder inequality for them.
In the Euclidean case, if
![]() $p=q=2$
and
$p=q=2$
and
![]() $m\equiv 1$
, in [Reference Chiti15, Reference Chiti16], Chiti proves the following inequality for the first eigenfunctions
$m\equiv 1$
, in [Reference Chiti15, Reference Chiti16], Chiti proves the following inequality for the first eigenfunctions
![]() $v$
corresponding to the first Dirichlet eigenvalue of the Laplace operator
$v$
corresponding to the first Dirichlet eigenvalue of the Laplace operator
![]() $\lambda ^{\mathcal E}_2(\Omega )\equiv \lambda (\Omega )$
:
$\lambda ^{\mathcal E}_2(\Omega )\equiv \lambda (\Omega )$
:
and the equality case is achieved if and only if
![]() $\Omega$
is a ball and
$\Omega$
is a ball and
![]() $v=v^\sharp$
, where the symbol “
$v=v^\sharp$
, where the symbol “
![]() $^\sharp$
” denotes the Schwarz symmetral of a function (see [Reference Kesavan30]). In [Reference Alvino, Ferone and Trombetti3], the authors prove (1.5) for the first eigenfunctions of the
$^\sharp$
” denotes the Schwarz symmetral of a function (see [Reference Kesavan30]). In [Reference Alvino, Ferone and Trombetti3], the authors prove (1.5) for the first eigenfunctions of the
![]() $p$
-Laplacian. Moreover, in [Reference Alberico, Ferone and Volpicelli1], the authors extend the result to the weighted case, and the inequality reads as follows:
$p$
-Laplacian. Moreover, in [Reference Alberico, Ferone and Volpicelli1], the authors extend the result to the weighted case, and the inequality reads as follows:
The equality sign holds if and only if
![]() $\Omega$
is a ball,
$\Omega$
is a ball,
![]() $v=v^\sharp$
and
$v=v^\sharp$
and
![]() $m=m^\sharp$
, modulo translation. In the general case
$m=m^\sharp$
, modulo translation. In the general case
![]() $p \neq q$
, in the Euclidean case, a Chiti type inequality is proved in the case
$p \neq q$
, in the Euclidean case, a Chiti type inequality is proved in the case
![]() $m\equiv 1$
in [Reference Carroll and Ratzkin14] and [Reference Carroll, Fall and Ratzkin13] when
$m\equiv 1$
in [Reference Carroll and Ratzkin14] and [Reference Carroll, Fall and Ratzkin13] when
![]() $p=2$
and for any
$p=2$
and for any
![]() $p$
, respectively. More precisely in [Reference Carroll, Fall and Ratzkin13], the authors prove the following inequality:
$p$
, respectively. More precisely in [Reference Carroll, Fall and Ratzkin13], the authors prove the following inequality:
Even in this case, the equality sign holds if and only if
![]() $\Omega$
is a ball and
$\Omega$
is a ball and
![]() $v=v^\sharp$
, modulo translation. The goal of this paper is to prove a Chiti type inequality in the spirit of (1.6) and (1.7) for the first eigenfunctions of the general weighted eigenvalue problem (1.2). We recall that, when
$v=v^\sharp$
, modulo translation. The goal of this paper is to prove a Chiti type inequality in the spirit of (1.6) and (1.7) for the first eigenfunctions of the general weighted eigenvalue problem (1.2). We recall that, when
![]() $p=q$
and
$p=q$
and
![]() $m\equiv 1$
, the result in the anisotropic setting has been proved in [Reference Belloni, Ferone and Kawohl9]. Our main theorem is the following.
$m\equiv 1$
, the result in the anisotropic setting has been proved in [Reference Belloni, Ferone and Kawohl9]. Our main theorem is the following.
Theorem 1.1. Let
![]() $\Omega \subset \mathbb R^n$
be an open, bounded, and connected set. Let
$\Omega \subset \mathbb R^n$
be an open, bounded, and connected set. Let
![]() $1\lt q\,{\leqslant}\, p$
, and let
$1\lt q\,{\leqslant}\, p$
, and let
![]() $u$
be an eigenfunction corresponding to the first eigenvalue (1.1). Then the following statements hold
$u$
be an eigenfunction corresponding to the first eigenvalue (1.1). Then the following statements hold
-
i) There exists a constant
 $C=C(p,q,r,n,\lambda ^{H}_{p,q}(\Omega ))$
such that(1.8)
$C=C(p,q,r,n,\lambda ^{H}_{p,q}(\Omega ))$
such that(1.8) \begin{equation} \|u \|_{L^r(\Omega, m)} \,{\leqslant}\, C\,\,\| u\|_{L^q(\Omega, m)}, \quad q\,{\leqslant}\, r; \end{equation}
\begin{equation} \|u \|_{L^r(\Omega, m)} \,{\leqslant}\, C\,\,\| u\|_{L^q(\Omega, m)}, \quad q\,{\leqslant}\, r; \end{equation}
-
ii) There exists a constant
 $C=C(p,q,r,n,\lambda ^{H}_{p,q}(\Omega ))$
such that(1.9)
$C=C(p,q,r,n,\lambda ^{H}_{p,q}(\Omega ))$
such that(1.9) \begin{equation} \|u\|_{L^\infty (\Omega )} \,{\leqslant}\, C \|u\|_{L^r(\Omega, m)} \quad 1\,{\leqslant}\, r\lt \infty . \end{equation}
\begin{equation} \|u\|_{L^\infty (\Omega )} \,{\leqslant}\, C \|u\|_{L^r(\Omega, m)} \quad 1\,{\leqslant}\, r\lt \infty . \end{equation}
The equality cases hold if and only if
![]() $\Omega$
is a Wulff shape and
$\Omega$
is a Wulff shape and
![]() $u$
and
$u$
and
![]() $m$
coincide, that is, in
$m$
coincide, that is, in
![]() $\Omega$
with their convex symmetrization, modulo translation.
$\Omega$
with their convex symmetrization, modulo translation.
We stress that this result gives, in particular, a Chiti type inequality for the eigenfunctions corresponding to the first weighted eigenvalue of the anisotropic
![]() $p$
-Laplacian and extend (1.7) to the weighted case. The proof is based on symmetrization techniques and a comparison between the eigenfunctions corresponding to the first eigenvalue (1.1) and the first eigenfunctions of a suitable symmetrical eigenvalue problem.
$p$
-Laplacian and extend (1.7) to the weighted case. The proof is based on symmetrization techniques and a comparison between the eigenfunctions corresponding to the first eigenvalue (1.1) and the first eigenfunctions of a suitable symmetrical eigenvalue problem.
The structure of the paper is the following. In Section 2, we fix some notation, recall some basic properties of the Finsler norms, and give a brief overview about convex symmetrization. In Section 3, we study the main properties of
![]() $\lambda ^H_{p,q}(\Omega )$
and a Faber–Krahn type inequality. In the last section, we prove Theorem 1.1 by using symmetrization arguments.
$\lambda ^H_{p,q}(\Omega )$
and a Faber–Krahn type inequality. In the last section, we prove Theorem 1.1 by using symmetrization arguments.
2. Notations and preliminaries
Throughout this article,
![]() $|\cdot |$
denotes the Euclidean norm in
$|\cdot |$
denotes the Euclidean norm in
![]() $\mathbb{R}^n$
, while
$\mathbb{R}^n$
, while
![]() $\cdot$
is the standard Euclidean scalar product for
$\cdot$
is the standard Euclidean scalar product for
![]() $n\geqslant 2$
. Moreover, we denote by
$n\geqslant 2$
. Moreover, we denote by
![]() $|\Omega |$
the Lebesgue measure of
$|\Omega |$
the Lebesgue measure of
![]() $\Omega \subseteq \mathbb{R}^n$
, by
$\Omega \subseteq \mathbb{R}^n$
, by
![]() $B_R$
the Euclidean ball centered at the origin with radius
$B_R$
the Euclidean ball centered at the origin with radius
![]() $R$
and by
$R$
and by
![]() $\omega _n$
the measure of the unit ball.
$\omega _n$
the measure of the unit ball.
Let
![]() $E\subseteq \mathbb{R}^n$
be a bounded, open set and
$E\subseteq \mathbb{R}^n$
be a bounded, open set and
![]() $\Omega \subseteq \mathbb{R}^{n}$
be a measurable set. We recall now the definition of the perimeter of
$\Omega \subseteq \mathbb{R}^{n}$
be a measurable set. We recall now the definition of the perimeter of
![]() $\Omega$
in
$\Omega$
in
![]() $E$
in the sense of De Giorgi, that is,
$E$
in the sense of De Giorgi, that is,
The perimeter of
![]() $\Omega$
in
$\Omega$
in
![]() $\mathbb{R}^n$
will be denoted by
$\mathbb{R}^n$
will be denoted by
![]() $P(\Omega )$
and, if
$P(\Omega )$
and, if
![]() $P(\Omega )\lt \infty$
, we say that
$P(\Omega )\lt \infty$
, we say that
![]() $\Omega$
is a set of finite perimeter. Some results relative to the sets of finite perimeter are contained, for instance, in [Reference Maggi31]. Moreover, if
$\Omega$
is a set of finite perimeter. Some results relative to the sets of finite perimeter are contained, for instance, in [Reference Maggi31]. Moreover, if
![]() $\Omega$
has Lipschitz boundary, we have that
$\Omega$
has Lipschitz boundary, we have that
2.1. The anisotropic norm
Let
![]() $H\;:\;\mathbb{R}^n \longrightarrow [0,+\infty [$
,
$H\;:\;\mathbb{R}^n \longrightarrow [0,+\infty [$
,
![]() $n\,{\geqslant}\, 2$
, be a
$n\,{\geqslant}\, 2$
, be a
![]() $C^1(\mathbb{R}^n \setminus \{0\})$
convex function which is positively
$C^1(\mathbb{R}^n \setminus \{0\})$
convex function which is positively
![]() $1$
-homogeneous, that is,
$1$
-homogeneous, that is,
Moreover, let
![]() $0\lt \gamma \,{\leqslant}\, \delta$
be positive constants such that
$0\lt \gamma \,{\leqslant}\, \delta$
be positive constants such that
These properties guarantee that
![]() $H$
is a norm in
$H$
is a norm in
![]() $\mathbb{R}^n$
. Indeed by (2.2), we have that
$\mathbb{R}^n$
. Indeed by (2.2), we have that
![]() $H(\xi )=0$
if and only if
$H(\xi )=0$
if and only if
![]() $\xi = 0$
. It is homogeneous by (2.1) and the triangular inequality is a consequence of the convexity of the function
$\xi = 0$
. It is homogeneous by (2.1) and the triangular inequality is a consequence of the convexity of the function
![]() $H$
: if
$H$
: if
![]() $\xi, \eta \in \mathbb{R}^n$
, then
$\xi, \eta \in \mathbb{R}^n$
, then
Because of (2.1), we can assume that the set
is such that
![]() $|K|=\omega _n$
, where
$|K|=\omega _n$
, where
![]() $\omega _n$
is the measure of the unit sphere in
$\omega _n$
is the measure of the unit sphere in
![]() $\mathbb{R}^n$
. We can define the support function of
$\mathbb{R}^n$
. We can define the support function of
![]() $K$
as:
$K$
as:
where
![]() $\left \lt \cdot, \cdot \right \gt$
denotes the scalar product in
$\left \lt \cdot, \cdot \right \gt$
denotes the scalar product in
![]() $\mathbb{R}^n$
.
$\mathbb{R}^n$
.
![]() $H^{\circ }\;:\;\mathbb{R}^n \longrightarrow [0,+\infty ]$
is a convex, homogeneous function in the sense of (2.1). Moreover,
$H^{\circ }\;:\;\mathbb{R}^n \longrightarrow [0,+\infty ]$
is a convex, homogeneous function in the sense of (2.1). Moreover,
![]() $H$
and
$H$
and
![]() $H^{\circ }$
are polar to each other, in the sense that
$H^{\circ }$
are polar to each other, in the sense that
and
![]() $H$
is the support function of the set:
$H$
is the support function of the set:
The set
![]() $\mathcal{W}=\{x \in \mathbb{R}^n \;:\; H^{\circ }(x)\lt 1 \}$
is the so-called Wulff shape centered at the origin. We set
$\mathcal{W}=\{x \in \mathbb{R}^n \;:\; H^{\circ }(x)\lt 1 \}$
is the so-called Wulff shape centered at the origin. We set
![]() $k_n = |\mathcal{W}|$
. More generally, we will denote by
$k_n = |\mathcal{W}|$
. More generally, we will denote by
![]() $\mathcal{W}_R(x_0)$
the Wulff shape centered in
$\mathcal{W}_R(x_0)$
the Wulff shape centered in
![]() $x_0 \in \mathbb{R}^n$
the set
$x_0 \in \mathbb{R}^n$
the set
![]() $R\mathcal{W}+x_0$
, and
$R\mathcal{W}+x_0$
, and
![]() $\mathcal{W}_R(0)=\mathcal{W}_R$
.
$\mathcal{W}_R(0)=\mathcal{W}_R$
.
The following properties hold for
![]() $H$
and
$H$
and
![]() $H^{\circ }$
:
$H^{\circ }$
:
An example of an anisotropic norm that satisfies the above-mentioned properties is the following. Let
![]() $r\in (1,+\infty )$
and let us consider
$r\in (1,+\infty )$
and let us consider
known in literature also as
![]() $r$
-norm. With this choice, the highly nonlinear operator
$r$
-norm. With this choice, the highly nonlinear operator
![]() $\mathcal{L}_p(u)$
, defined in (1.3), becomes
$\mathcal{L}_p(u)$
, defined in (1.3), becomes
We stress that for
![]() $r=p$
,
$r=p$
,
![]() $\mathcal{L}_p(u)$
is the so called pseudo-
$\mathcal{L}_p(u)$
is the so called pseudo-
![]() $p$
-Laplace operator. Examples of non-smooth anisotropic norm can be found in [Reference Bellettini, Caselles, Chambolle and Novaga8] and references therein, where the authors consider a crystalline anisotropy and the associated Wulff shape is a polyhedron.
$p$
-Laplace operator. Examples of non-smooth anisotropic norm can be found in [Reference Bellettini, Caselles, Chambolle and Novaga8] and references therein, where the authors consider a crystalline anisotropy and the associated Wulff shape is a polyhedron.
If
![]() $E \subset \mathbb{R}^n$
is an open, bounded set with Lipschitz boundary and
$E \subset \mathbb{R}^n$
is an open, bounded set with Lipschitz boundary and
![]() $\Omega$
is an open subset of
$\Omega$
is an open subset of
![]() $\mathbb{R}^n$
, we can give a generalized definition of perimeter of
$\mathbb{R}^n$
, we can give a generalized definition of perimeter of
![]() $\Omega$
with respect to the anisotropic norm as follows (see for instance [Reference Amar and Bellettini6]):
$\Omega$
with respect to the anisotropic norm as follows (see for instance [Reference Amar and Bellettini6]):
where
![]() $\partial ^*\Omega$
is the reduced boundary of
$\partial ^*\Omega$
is the reduced boundary of
![]() $\Omega$
(for the definition see [Reference Evans and Gariepy21]),
$\Omega$
(for the definition see [Reference Evans and Gariepy21]),
![]() $\nu$
is its Euclidean outer normal, and
$\nu$
is its Euclidean outer normal, and
![]() $\mathcal{H}^{n-1}$
is the
$\mathcal{H}^{n-1}$
is the
![]() $(n-1)-$
dimensional Hausdorff measure in
$(n-1)-$
dimensional Hausdorff measure in
![]() $\mathbb{R}^n$
. Clearly, if
$\mathbb{R}^n$
. Clearly, if
![]() $E$
is open, bounded and Lipschitz, then the outer unit normal exists almost everywhere and
$E$
is open, bounded and Lipschitz, then the outer unit normal exists almost everywhere and
By (2.2), we have that
In [Reference Alvino, Trombetti and Lions5], it is shown that if
![]() $u\in W^{1,1}(\Omega )$
, then for, that is,
$u\in W^{1,1}(\Omega )$
, then for, that is,
![]() $t\gt 0$
$t\gt 0$
Moreover, an isoperimetric inequality for the anisotropic perimeter holds (for instance see [Reference Alvino, Ferone, Lions and Trombetti2, Reference Busemann12, Reference Dacorogna and Pfister18, Reference Figalli, Maggi and Pratelli23, Reference Fonseca and Müller24])
2.2. Convex symmetrization
Let
![]() $\Omega \subset \mathbb{R}^n$
be an open, bounded, and connected set. Let
$\Omega \subset \mathbb{R}^n$
be an open, bounded, and connected set. Let
![]() $f: \Omega \longrightarrow [0,+\infty ]$
be a measurable function. The decreasing rearrangement
$f: \Omega \longrightarrow [0,+\infty ]$
be a measurable function. The decreasing rearrangement
![]() $f^*$
of
$f^*$
of
![]() $f$
is defined as follows:
$f$
is defined as follows:
where
is the distribution function of
![]() $f$
. We recall that the Schwarz symmetrand of
$f$
. We recall that the Schwarz symmetrand of
![]() $f$
is a radially spherically function defined as follows:
$f$
is a radially spherically function defined as follows:
where
![]() $\Omega ^{\sharp }$
is the ball centered at the origin such that
$\Omega ^{\sharp }$
is the ball centered at the origin such that
![]() $|\Omega ^{\sharp }|=|\Omega |$
. The convex symmetrization
$|\Omega ^{\sharp }|=|\Omega |$
. The convex symmetrization
![]() $f^{\star }$
of
$f^{\star }$
of
![]() $f$
, instead, is a function symmetric with respect to
$f$
, instead, is a function symmetric with respect to
![]() $H^{\circ }$
defined as follows:
$H^{\circ }$
defined as follows:
where
![]() $\Omega ^\star$
is a Wulff shape centered at the origin and such that
$\Omega ^\star$
is a Wulff shape centered at the origin and such that
![]() $|\Omega ^{\star }|=|\Omega |$
(see [Reference Alvino, Ferone, Lions and Trombetti2]). We stress that both
$|\Omega ^{\star }|=|\Omega |$
(see [Reference Alvino, Ferone, Lions and Trombetti2]). We stress that both
![]() $f^{\star }$
and
$f^{\star }$
and
![]() $f^{\sharp }$
are defined by means the decreasing rearrangement
$f^{\sharp }$
are defined by means the decreasing rearrangement
![]() $f^*$
, but they have different symmetry. In particular, it is well known that the functions
$f^*$
, but they have different symmetry. In particular, it is well known that the functions
![]() $f$
,
$f$
,
![]() $f^*$
,
$f^*$
,
![]() $f^{\sharp }$
, and
$f^{\sharp }$
, and
![]() $f^{\star }$
are equimeasurable, that is,
$f^{\star }$
are equimeasurable, that is,
As a consequence, if
![]() $f\in L^p(\Omega )$
,
$f\in L^p(\Omega )$
,
![]() $p\,{\geqslant}\, 1$
, then
$p\,{\geqslant}\, 1$
, then
Regarding the norm of the gradient, a generalized version of the well-known Pólya–Szegö inequality holds and it states (see for instance [Reference Alvino, Ferone, Lions and Trombetti2])
Theorem 2.1. (Pólya–Szegö principle). If
![]() $w \in W^{1,p}_0(\Omega )$
for
$w \in W^{1,p}_0(\Omega )$
for
![]() $p\,{\geqslant}\, 1$
, then we have that
$p\,{\geqslant}\, 1$
, then we have that
where
![]() $\Omega ^\star$
is the Wulff Shape such that
$\Omega ^\star$
is the Wulff Shape such that
![]() $|\Omega ^\star |=|\Omega |$
.
$|\Omega ^\star |=|\Omega |$
.
For the sake of completeness, we will state the result concerning the equality case of the Pólya–Szegö inequality, whose proof is contained in [Reference Ferone and Volpicelli22] for the generic anisotropic case and in [Reference Ziemer and Brothers38] for the Euclidean case.
Theorem 2.2. Let
![]() $u$
be a non-negative function in
$u$
be a non-negative function in
![]() $W^{1,p}(\mathbb{R}^n)$
, for
$W^{1,p}(\mathbb{R}^n)$
, for
![]() $1\lt p\lt +\infty$
, such that
$1\lt p\lt +\infty$
, such that
Then
if and only if
![]() $u=u^\star$
a.e. in
$u=u^\star$
a.e. in
![]() $\mathbb{R}^n$
, up to translations.
$\mathbb{R}^n$
, up to translations.
Obviously, Theorem 2.2 can holds true in the case of a
![]() $W^{1,p}_0(\Omega )$
function.
$W^{1,p}_0(\Omega )$
function.
We conclude this section by recalling some known properties about rearrangements that we will use in the proof of the main theorem. The following result is the well-known Hardy–Littlewood inequality (see [Reference Kesavan30]):
So, if we consider
![]() $g$
as the characteristic function of the set
$g$
as the characteristic function of the set
![]() $\{x\in \Omega \;:\; u(x)\gt t\}$
, for some measurable function
$\{x\in \Omega \;:\; u(x)\gt t\}$
, for some measurable function
![]() $u\;:\;\Omega \rightarrow \mathbb{R}$
and
$u\;:\;\Omega \rightarrow \mathbb{R}$
and
![]() $t\,{\geqslant}\, 0$
, then we get
$t\,{\geqslant}\, 0$
, then we get
where, again,
![]() $\mu (t)$
is the distribution function of
$\mu (t)$
is the distribution function of
![]() $u$
. Finally, we recall the definition of dominated rearrangements (see for instance [Reference Alvino, Lions and Trombetti4] and [Reference Chong and Rice17]).
$u$
. Finally, we recall the definition of dominated rearrangements (see for instance [Reference Alvino, Lions and Trombetti4] and [Reference Chong and Rice17]).
Definition 2.3. Let
![]() $f,g \in L^1(\Omega )$
be nonnegative functions. We say that
$f,g \in L^1(\Omega )$
be nonnegative functions. We say that
![]() $g$
is dominated by
$g$
is dominated by
![]() $f$
and write
$f$
and write
![]() $g\prec f$
if the following two statements hold
$g\prec f$
if the following two statements hold
-
(i)
 $\displaystyle \int _{0}^s g^* (t)\,dt \,{\leqslant}\, \displaystyle \int _{0}^s f^* (t)\,dt$
;
$\displaystyle \int _{0}^s g^* (t)\,dt \,{\leqslant}\, \displaystyle \int _{0}^s f^* (t)\,dt$
; -
(ii)
 $\displaystyle \int _{0}^{|\Omega |} g^* (t)\,dt =\displaystyle \int _{0}^{|\Omega |} f^* (t)\,dt$
.
$\displaystyle \int _{0}^{|\Omega |} g^* (t)\,dt =\displaystyle \int _{0}^{|\Omega |} f^* (t)\,dt$
.
In [Reference Alvino, Lions and Trombetti4], the authors prove the following result:
Proposition 2.4. Let
![]() $f,g,h$
be positive and such that
$f,g,h$
be positive and such that
![]() $hf, hg\in L^1(\Omega )$
. Let
$hf, hg\in L^1(\Omega )$
. Let
![]() $F$
be a convex, nonnegative function such that
$F$
be a convex, nonnegative function such that
![]() $F(0)=0$
. If
$F(0)=0$
. If
![]() $hg \prec hf$
Then
$hg \prec hf$
Then
Moreover, if
![]() $F$
is strictly convex, the equality holds if and only if
$F$
is strictly convex, the equality holds if and only if
![]() $f^*\equiv g^*$
, that is, in
$f^*\equiv g^*$
, that is, in
![]() $[0,|\Omega |]$
.
$[0,|\Omega |]$
.
3. The (p,q)-anisotropic Laplacian
In this section, we study the main properties of (1.1) and the corresponding minimizers. Let
![]() $\Omega \subset \mathbb{R}^n$
,
$\Omega \subset \mathbb{R}^n$
,
![]() $n\,{\geqslant}\, 2$
be an open, bounded, and connected set. Let
$n\,{\geqslant}\, 2$
be an open, bounded, and connected set. Let
![]() $m\in L^{\infty }(\Omega )$
be a positive function and
$m\in L^{\infty }(\Omega )$
be a positive function and
![]() $p, q$
be such that
$p, q$
be such that
![]() $1\lt p\lt \infty$
and
$1\lt p\lt \infty$
and
![]() $1\lt q\lt p^*$
, where
$1\lt q\lt p^*$
, where
![]() $p^*=np/(n-p)$
, if
$p^*=np/(n-p)$
, if
![]() $p\lt n$
, and
$p\lt n$
, and
![]() $p^*=\infty$
, if
$p^*=\infty$
, if
![]() $p\,{\geqslant}\, n$
. A function
$p\,{\geqslant}\, n$
. A function
![]() $v\in W_0^{1,p}(\Omega )$
is a weak solution to the problem (1.2) corresponding to
$v\in W_0^{1,p}(\Omega )$
is a weak solution to the problem (1.2) corresponding to
![]() $\lambda$
if
$\lambda$
if
for every
![]() $\varphi \in W_0^{1,p}(\Omega )$
. By standard argument of calculus of variations, it is not difficult to prove the following result:
$\varphi \in W_0^{1,p}(\Omega )$
. By standard argument of calculus of variations, it is not difficult to prove the following result:
Theorem 3.1. Let
![]() $n\,{\geqslant}\, 2$
and
$n\,{\geqslant}\, 2$
and
![]() $\Omega \subset \mathbb{R}^n$
, be an open, bounded set and let
$\Omega \subset \mathbb{R}^n$
, be an open, bounded set and let
![]() $p,q$
and
$p,q$
and
![]() $m$
be as above. Then
$m$
be as above. Then
![]() $\lambda ^H_{p,q}(\Omega )$
, defined in (1.1), is strictly positive and actually a minimum. Moreover, any minimizer is a weak solution to the problem (1.2), with
$\lambda ^H_{p,q}(\Omega )$
, defined in (1.1), is strictly positive and actually a minimum. Moreover, any minimizer is a weak solution to the problem (1.2), with
![]() $\lambda =\lambda ^H_{p,q}(\Omega )$
, and has constant sign on every connected component.
$\lambda =\lambda ^H_{p,q}(\Omega )$
, and has constant sign on every connected component.
As regard the simplicity, we have
Theorem 3.2. Let
![]() $n\,{\geqslant}\, 2$
and
$n\,{\geqslant}\, 2$
and
![]() $\Omega \subset \mathbb{R}^n$
, be an open, bounded, and connected set and let
$\Omega \subset \mathbb{R}^n$
, be an open, bounded, and connected set and let
![]() $p$
and
$p$
and
![]() $m$
be as above and let
$m$
be as above and let
![]() $1\lt q\,{\leqslant}\, p$
. Then
$1\lt q\,{\leqslant}\, p$
. Then
![]() $\lambda ^H_{p,q}(\Omega )$
is simple, that is, there exists a unique corresponding eigenfunction up to multiplicative constants.
$\lambda ^H_{p,q}(\Omega )$
is simple, that is, there exists a unique corresponding eigenfunction up to multiplicative constants.
The proof of the previous result is contained in [Reference Kawohl, Lucia and Prashanth29], where the authors consider a more general class of quasilinear operators. We stress that this result was already proved when
![]() $H=\mathcal{E}$
and
$H=\mathcal{E}$
and
![]() $m\equiv 1$
in the paper [Reference Kawohl28] and in the case of a positive and essentially bounded weight in [Reference Nazarov33]. Finally, we have the following:
$m\equiv 1$
in the paper [Reference Kawohl28] and in the case of a positive and essentially bounded weight in [Reference Nazarov33]. Finally, we have the following:
Theorem 3.3. Let
![]() $n\,{\geqslant}\, 2$
and let
$n\,{\geqslant}\, 2$
and let
![]() $\Omega \subset \mathbb{R}^n$
be an open, bounded, and connected set. Let
$\Omega \subset \mathbb{R}^n$
be an open, bounded, and connected set. Let
![]() $p$
and
$p$
and
![]() $m$
be as above and let
$m$
be as above and let
![]() $1\lt q\,{\leqslant}\, p$
. Any nonnegative function
$1\lt q\,{\leqslant}\, p$
. Any nonnegative function
![]() $v \in W_0^{1,p}(\Omega )$
, which is a weak solution to the problem (1.2), for some
$v \in W_0^{1,p}(\Omega )$
, which is a weak solution to the problem (1.2), for some
![]() $\lambda \gt 0$
, is a first eigenfunction, that is
$\lambda \gt 0$
, is a first eigenfunction, that is
![]() $\lambda =\lambda ^H_{p,q}(\Omega )$
.
$\lambda =\lambda ^H_{p,q}(\Omega )$
.
Proof. The proof is similar to the one contained in [Reference Brasco and Franzina10, Theorem 5.1], and it follows standard arguments and a general Picone inequality. For the reader convenience and sake of completeness, we write the main steps. Let
![]() $v$
be a non-negative weak solution to the problem (1.2) corresponding to
$v$
be a non-negative weak solution to the problem (1.2) corresponding to
![]() $\lambda$
. By the strong maximum principle, we have that
$\lambda$
. By the strong maximum principle, we have that
![]() $v\gt 0$
in
$v\gt 0$
in
![]() $\Omega .$
Let
$\Omega .$
Let
![]() $u$
be the first positive eigenfunction corresponding to
$u$
be the first positive eigenfunction corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
such that
$\lambda ^H_{p,q}(\Omega )$
such that
Then,
Being
![]() $v$
a weak positive solution to (1.2) corresponding to
$v$
a weak positive solution to (1.2) corresponding to
![]() $\lambda$
, we can chose
$\lambda$
, we can chose
![]() $\varphi =\displaystyle \frac{u^q}{v^{q-1}}$
as test function in (3.1) obtaining
$\varphi =\displaystyle \frac{u^q}{v^{q-1}}$
as test function in (3.1) obtaining
 \begin{align} \int _{\Omega }\left ((H(\nabla v)\right )^{p-1}H_{\xi }(\nabla v ) \cdot \nabla \left ( \frac{u^q}{v^{q-1}}\right )\,dx &=\lambda \|m^{\frac{1}{q}} v\|_q^{p-q}\int _{\Omega }m(x)\,u^q\,dx \nonumber \\[5pt] &= \lambda \left (\int _{\Omega }m(x) \,u^q \,dx \right )^{\frac pq}, \end{align}
\begin{align} \int _{\Omega }\left ((H(\nabla v)\right )^{p-1}H_{\xi }(\nabla v ) \cdot \nabla \left ( \frac{u^q}{v^{q-1}}\right )\,dx &=\lambda \|m^{\frac{1}{q}} v\|_q^{p-q}\int _{\Omega }m(x)\,u^q\,dx \nonumber \\[5pt] &= \lambda \left (\int _{\Omega }m(x) \,u^q \,dx \right )^{\frac pq}, \end{align}
where last equality follows by (3.2). In the left-hand side, we can apply the general Picone inequality (see Proposition 2.9 in [Reference Brasco and Franzina10]) and we have
By the Hölder inequality, the normalization (3.2) and (3.3) we get that
![]() $\lambda ^{H}_{p,q}(\Omega )\,{\geqslant}\, \lambda$
, that implies
$\lambda ^{H}_{p,q}(\Omega )\,{\geqslant}\, \lambda$
, that implies
![]() $u=v$
.
$u=v$
.
3.1. The case
 $\Omega = \mathcal{W}_R$
$\Omega = \mathcal{W}_R$
In this subsection, we study the problem (1.2) when
![]() $\Omega$
is a Wulff shape. In this case, the eigenfunctions inherit some symmetry properties. Let be
$\Omega$
is a Wulff shape. In this case, the eigenfunctions inherit some symmetry properties. Let be
![]() $\Omega = \mathcal{W}_R$
and let
$\Omega = \mathcal{W}_R$
and let
![]() $m\in L^{\infty }(\mathcal{W}_R)$
be a positive function such that
$m\in L^{\infty }(\mathcal{W}_R)$
be a positive function such that
![]() $m(x)=m^{\star }(x)$
. Then problem (1.2) becomes
$m(x)=m^{\star }(x)$
. Then problem (1.2) becomes
 \begin{equation} \begin{cases} -\mathcal{L}_{p}(v)=\lambda m^{\star }(x) \| v\|_{q, m^\star }^{p-q}|v|^{q-2}v & \mbox{in}\ \mathcal{W}_R\\[5pt] v=0&\mbox{on}\ \partial \mathcal{W}_R. \end{cases} \end{equation}
\begin{equation} \begin{cases} -\mathcal{L}_{p}(v)=\lambda m^{\star }(x) \| v\|_{q, m^\star }^{p-q}|v|^{q-2}v & \mbox{in}\ \mathcal{W}_R\\[5pt] v=0&\mbox{on}\ \partial \mathcal{W}_R. \end{cases} \end{equation}
The following result holds
Proposition 3.4. Let
![]() $1\lt p\lt \infty$
and
$1\lt p\lt \infty$
and
![]() $1\lt q\,{\leqslant}\, p$
. Let
$1\lt q\,{\leqslant}\, p$
. Let
![]() $v \in C^1(\overline{\Omega })\cap C^{1,\alpha }(\Omega )$
be a first positive eigenfunction to the problem (3.5). Then there exists a decreasing function
$v \in C^1(\overline{\Omega })\cap C^{1,\alpha }(\Omega )$
be a first positive eigenfunction to the problem (3.5). Then there exists a decreasing function
![]() $\rho (r)$
,
$\rho (r)$
,
![]() $r \in [0,R]$
, such that
$r \in [0,R]$
, such that
![]() $\rho \in C^{\infty }((0,R))\cap C^1([0,R])$
,
$\rho \in C^{\infty }((0,R))\cap C^1([0,R])$
,
![]() $\rho ^{\prime }(0)=0$
, and
$\rho ^{\prime }(0)=0$
, and
![]() $v(x)=\rho (H^o(x))$
.
$v(x)=\rho (H^o(x))$
.
Proof. By the simplicity, we can assume that
![]() $\|v\|_{L^q(\mathcal W_R,m^{\star })}=1$
. Let
$\|v\|_{L^q(\mathcal W_R,m^{\star })}=1$
. Let
![]() $B_R$
be the ball centered at the origin with radius
$B_R$
be the ball centered at the origin with radius
![]() $R\gt 0$
, and let us consider the weighted p-Laplace eigenvalue problem in
$R\gt 0$
, and let us consider the weighted p-Laplace eigenvalue problem in
![]() $B_R$
:
$B_R$
:
 \begin{equation} \begin{cases} -\Delta _p z=\lambda \tilde m(|x|)\|z\|_{q,m^{\star }}^{p-q}|z|^{q-2}z & \mbox{in}\ B_R\\[5pt] z=0&\mbox{on}\ \partial B_R, \end{cases} \end{equation}
\begin{equation} \begin{cases} -\Delta _p z=\lambda \tilde m(|x|)\|z\|_{q,m^{\star }}^{p-q}|z|^{q-2}z & \mbox{in}\ B_R\\[5pt] z=0&\mbox{on}\ \partial B_R, \end{cases} \end{equation}
where
![]() $\tilde m(r)=m^*(k_n r^n)$
,
$\tilde m(r)=m^*(k_n r^n)$
,
![]() $0 \,{\leqslant}\, r\,{\leqslant}\, R$
. Let
$0 \,{\leqslant}\, r\,{\leqslant}\, R$
. Let
![]() $z$
be the positive eigenfunction corresponding to the first eigenvalue
$z$
be the positive eigenfunction corresponding to the first eigenvalue
![]() $\lambda ^{\mathcal E}_{p,q}(B_R)$
to the problem (3.6), such that
$\lambda ^{\mathcal E}_{p,q}(B_R)$
to the problem (3.6), such that
![]() $\|z\|_{L^q(B_R,\tilde{m})}=\|v\|_{L^q(\mathcal W_R,m^{\star })}=1$
. Then uniqueness guarantees that
$\|z\|_{L^q(B_R,\tilde{m})}=\|v\|_{L^q(\mathcal W_R,m^{\star })}=1$
. Then uniqueness guarantees that
![]() $z$
is radially symmetric, which means that there exists a positive one-dimensional function
$z$
is radially symmetric, which means that there exists a positive one-dimensional function
![]() $\rho _p \;:\; r\in [0,R]\to \mathbb{R}^+$
such that
$\rho _p \;:\; r\in [0,R]\to \mathbb{R}^+$
such that
![]() $z(x)=\rho _p(|x|)$
, and
$z(x)=\rho _p(|x|)$
, and
![]() $\rho _p$
solves the following problem:
$\rho _p$
solves the following problem:
 \begin{equation} \begin{cases} -(p-1)|\rho ^{\prime }_p|^{p-2}\rho ^{\prime \prime }_p+\frac{n-1}{r}|\rho ^{\prime }_p|^{p-1}= \lambda ^{\mathcal E}_{p,q}(B_R)\tilde m|\rho _p|^{q-2}\rho _p,& r \in (0,R) \\[5pt] \rho ^{\prime }_p(0)=\rho _p(R)=0. \end{cases} \end{equation}
\begin{equation} \begin{cases} -(p-1)|\rho ^{\prime }_p|^{p-2}\rho ^{\prime \prime }_p+\frac{n-1}{r}|\rho ^{\prime }_p|^{p-1}= \lambda ^{\mathcal E}_{p,q}(B_R)\tilde m|\rho _p|^{q-2}\rho _p,& r \in (0,R) \\[5pt] \rho ^{\prime }_p(0)=\rho _p(R)=0. \end{cases} \end{equation}
In particular, integrating equation (3.7), it is possible to see that
![]() $\rho ^{\prime }_p$
is zero only when
$\rho ^{\prime }_p$
is zero only when
![]() $r=0$
and consequently that
$r=0$
and consequently that
![]() $\rho _p$
is strictly decreasing in
$\rho _p$
is strictly decreasing in
![]() $[0,R]$
. Now we can come back to the anisotropy. Indeed if we consider
$[0,R]$
. Now we can come back to the anisotropy. Indeed if we consider
![]() $w=\rho _p(H^\circ (x))$
, then using properties (2.4)-(2.6) and the regularity of
$w=\rho _p(H^\circ (x))$
, then using properties (2.4)-(2.6) and the regularity of
![]() $H$
, by construction, we obtain that
$H$
, by construction, we obtain that
![]() $w(x)$
is a solution to problem (3.5), which is positive and radial with respect to the anisotropic norm. The simplicity and Theorem 3.3 imply that
$w(x)$
is a solution to problem (3.5), which is positive and radial with respect to the anisotropic norm. The simplicity and Theorem 3.3 imply that
![]() $v=w$
, and this concludes the proof.
$v=w$
, and this concludes the proof.
Remark 3.5.
We stress that the proof of the previous result shows that the first eigenvalue
![]() $\lambda ^H_{p,q}(\mathcal W_R)$
coincides with the first eigenvalue of problem (3.6).
$\lambda ^H_{p,q}(\mathcal W_R)$
coincides with the first eigenvalue of problem (3.6).
3.2. A Faber–Krahn type inequality
Theorem 3.6. Let
![]() $\Omega \in \mathbb{R}^n$
,
$\Omega \in \mathbb{R}^n$
,
![]() $n\,{\geqslant}\, 2$
, be an open, bounded, and connected set and let
$n\,{\geqslant}\, 2$
, be an open, bounded, and connected set and let
![]() $1\lt q\,{\leqslant}\, p$
. Then
$1\lt q\,{\leqslant}\, p$
. Then
where
![]() $\Omega ^\star$
is the Wulff shape such that
$\Omega ^\star$
is the Wulff shape such that
![]() $|\Omega ^\star |=|\Omega |$
. The equality case holds if and only if
$|\Omega ^\star |=|\Omega |$
. The equality case holds if and only if
![]() $\Omega =\Omega ^{\star }$
and
$\Omega =\Omega ^{\star }$
and
![]() $m=m^{\star }$
, that is, in
$m=m^{\star }$
, that is, in
![]() $\Omega$
, up to translations, where
$\Omega$
, up to translations, where
![]() $m^{\star }$
is the convex symmetrization of
$m^{\star }$
is the convex symmetrization of
![]() $m$
.
$m$
.
Proof. We argue as in [Reference Belloni, Ferone and Kawohl9]. We observe that
![]() $\lambda ^H_{p,q}(\Omega ^{\star })$
has the following variational characterization:
$\lambda ^H_{p,q}(\Omega ^{\star })$
has the following variational characterization:
 \begin{equation} \lambda ^H_{p,q}(\Omega ^{\star }) = \inf _{\substack{w\in W^{1,p}_0(\Omega ^{\star }), \\ w \neq 0}}\frac{\displaystyle \int _{\Omega ^{\star }} H(\nabla w)^p\,dx}{\bigg (\displaystyle \int _{\Omega ^{\star }} m^{\star }|w|^q\, dx\bigg )^{\frac{p}{q}}}. \end{equation}
\begin{equation} \lambda ^H_{p,q}(\Omega ^{\star }) = \inf _{\substack{w\in W^{1,p}_0(\Omega ^{\star }), \\ w \neq 0}}\frac{\displaystyle \int _{\Omega ^{\star }} H(\nabla w)^p\,dx}{\bigg (\displaystyle \int _{\Omega ^{\star }} m^{\star }|w|^q\, dx\bigg )^{\frac{p}{q}}}. \end{equation}
The Faber–Krahn inequality is a straightforward application of the Pólya–Szegö principle and the Hardy–Littlewood inequality. Indeed if
![]() $u$
is a positive eigenfunction corresponding to
$u$
is a positive eigenfunction corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
, then
$\lambda ^H_{p,q}(\Omega )$
, then
 \begin{equation} \lambda ^H_{p,q}(\Omega ) = \frac{\displaystyle \int _\Omega H(\nabla u)^p\,dx}{\bigg (\displaystyle \int _\Omega m{u}^q\,dx\bigg )^{\frac{p}{q}}} \,{\geqslant}\, \frac{\displaystyle \int _{\Omega ^{\star }} H(\nabla u^{\star })^p\,dx}{\bigg (\displaystyle \int _{\Omega ^{\star }}m^{\star }(u^{\star })^q\,dx\bigg )^{\frac{p}{q}}}\,{\geqslant}\, \lambda ^H_{p,q}(\Omega ^{\star }). \end{equation}
\begin{equation} \lambda ^H_{p,q}(\Omega ) = \frac{\displaystyle \int _\Omega H(\nabla u)^p\,dx}{\bigg (\displaystyle \int _\Omega m{u}^q\,dx\bigg )^{\frac{p}{q}}} \,{\geqslant}\, \frac{\displaystyle \int _{\Omega ^{\star }} H(\nabla u^{\star })^p\,dx}{\bigg (\displaystyle \int _{\Omega ^{\star }}m^{\star }(u^{\star })^q\,dx\bigg )^{\frac{p}{q}}}\,{\geqslant}\, \lambda ^H_{p,q}(\Omega ^{\star }). \end{equation}
Let us now consider the equality case. From (3.10), Pólya–Szegö principle and Hardy–Littlewood inequality, we get
 \begin{equation*} 1\,{\leqslant}\, \frac {\displaystyle \int _\Omega H(\nabla u)^p\,dx}{\displaystyle \int _{\Omega ^{\star }} H(\nabla u^{\star })^p\,dx}= \frac {\bigg (\displaystyle \int _{\Omega ^{\star }} m^{\star }(u^{\star })^q\,dx\bigg )^{\frac {p}{q}}}{\bigg (\displaystyle \int _\Omega m u^q\,dx\bigg )^{\frac {p}{q}}}\,{\leqslant}\, 1. \end{equation*}
\begin{equation*} 1\,{\leqslant}\, \frac {\displaystyle \int _\Omega H(\nabla u)^p\,dx}{\displaystyle \int _{\Omega ^{\star }} H(\nabla u^{\star })^p\,dx}= \frac {\bigg (\displaystyle \int _{\Omega ^{\star }} m^{\star }(u^{\star })^q\,dx\bigg )^{\frac {p}{q}}}{\bigg (\displaystyle \int _\Omega m u^q\,dx\bigg )^{\frac {p}{q}}}\,{\leqslant}\, 1. \end{equation*}
It follows that
and
4. A Chiti type inequality
In this section, we prove a reverse Hölder inequality for the eigenfunctions corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
. We first prove the following proposition as in the spirit of the Talenti result contained in [Reference Talenti37] (see also [Reference Alberico, Ferone and Volpicelli1–Reference Alvino, Ferone and Trombetti3, Reference Amato, Barbato, Masiello and Paoli7, Reference Sannipoli36]).
$\lambda ^H_{p,q}(\Omega )$
. We first prove the following proposition as in the spirit of the Talenti result contained in [Reference Talenti37] (see also [Reference Alberico, Ferone and Volpicelli1–Reference Alvino, Ferone and Trombetti3, Reference Amato, Barbato, Masiello and Paoli7, Reference Sannipoli36]).
Proposition 4.1. Let
![]() $\Omega \subset \mathbb{R}^n$
,
$\Omega \subset \mathbb{R}^n$
,
![]() $n\,{\geqslant}\, 2$
, be an open, bounded, and connected set,
$n\,{\geqslant}\, 2$
, be an open, bounded, and connected set,
![]() $1\lt q\,{\leqslant}\, p$
, and let
$1\lt q\,{\leqslant}\, p$
, and let
![]() $m\in L^{\infty }(\Omega )$
be a positive function. Let
$m\in L^{\infty }(\Omega )$
be a positive function. Let
![]() $u$
be a positive eigenfunction corresponding to
$u$
be a positive eigenfunction corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
. Then we have that
$\lambda ^H_{p,q}(\Omega )$
. Then we have that
In particular, the equality case holds if and only if
![]() $\Omega = \Omega ^{\star }$
and
$\Omega = \Omega ^{\star }$
and
![]() $m=m^{\star }$
, that is, in
$m=m^{\star }$
, that is, in
![]() $\Omega$
, up to translations, where
$\Omega$
, up to translations, where
![]() $m^{\star }$
is the convex symmetrization of
$m^{\star }$
is the convex symmetrization of
![]() $m$
.
$m$
.
Proof. We argue exactly as in the proof of [Reference Belloni, Ferone and Kawohl9, Lemma 3.6]. Let
![]() $u$
be a weak solution to the problem (1.2) corresponding to the first eigenvalue
$u$
be a weak solution to the problem (1.2) corresponding to the first eigenvalue
![]() $\lambda ^H_{p,q}(\Omega )$
, that is,
$\lambda ^H_{p,q}(\Omega )$
, that is,
 \begin{equation*} \begin {cases} -\mathcal {L}_{p}(u)=\lambda ^H_{p,q}(\Omega ) m\| u\|_{q,m}^{p-q}u^{q-1} & \mbox {in}\ \Omega \\[5pt] u=0&\mbox {on}\ \partial \Omega . \end {cases} \end{equation*}
\begin{equation*} \begin {cases} -\mathcal {L}_{p}(u)=\lambda ^H_{p,q}(\Omega ) m\| u\|_{q,m}^{p-q}u^{q-1} & \mbox {in}\ \Omega \\[5pt] u=0&\mbox {on}\ \partial \Omega . \end {cases} \end{equation*}
Let
![]() $t,h\gt 0$
and let us choose as a test function in (3.1) the following function in
$t,h\gt 0$
and let us choose as a test function in (3.1) the following function in
![]() $W^{1,p}_0(\Omega )$
:
$W^{1,p}_0(\Omega )$
:
 \begin{equation*} \varphi _h = \begin {cases} 0 & u\,{\leqslant}\, t\\[5pt] u-t & t\lt u\,{\leqslant}\, t+h\\[5pt] h & u\gt t+h. \end {cases} \end{equation*}
\begin{equation*} \varphi _h = \begin {cases} 0 & u\,{\leqslant}\, t\\[5pt] u-t & t\lt u\,{\leqslant}\, t+h\\[5pt] h & u\gt t+h. \end {cases} \end{equation*}
By standard arguments, we have
Recalling that the anisotropic perimeter can be written as follows:
by Hölder inequality, we get
Therefore, the isoperimetric inequality (2.9) gives
Since
![]() $\mu ^{\prime }(t)=\frac{1}{{u^*}^{\prime }(\mu (t))}$
and (4.2) holds true, we have
$\mu ^{\prime }(t)=\frac{1}{{u^*}^{\prime }(\mu (t))}$
and (4.2) holds true, we have
Using (2.12) and calling
![]() $s=\mu (t)$
, we have
$s=\mu (t)$
, we have
An application of the Hardy–Littlewood inequality gives the desired result.
The main tool we use in order to prove Theorem 1.1 is a suitable comparison result between
![]() $u$
and an eigenfunction
$u$
and an eigenfunction
![]() $z$
of a suitable eigenvalue problem. More precisely, let
$z$
of a suitable eigenvalue problem. More precisely, let
![]() $\Omega ^{\star }_\lambda$
be the Wulff shape centered at the origin such that
$\Omega ^{\star }_\lambda$
be the Wulff shape centered at the origin such that
![]() $\lambda ^H_{p,q}(\Omega )$
is the first eigenvalue to the following symmetric problem:
$\lambda ^H_{p,q}(\Omega )$
is the first eigenvalue to the following symmetric problem:
 \begin{equation} \begin{cases} -\mathcal{L}_{p}(z)=\mu m^\star \| z\|_{q,m^\star }^{p-q}z^{q-1} & \mbox{in}\ \Omega ^{\star }_\lambda \\[5pt] z=0&\mbox{on}\ \partial \Omega ^{\star }_\lambda, \end{cases} \end{equation}
\begin{equation} \begin{cases} -\mathcal{L}_{p}(z)=\mu m^\star \| z\|_{q,m^\star }^{p-q}z^{q-1} & \mbox{in}\ \Omega ^{\star }_\lambda \\[5pt] z=0&\mbox{on}\ \partial \Omega ^{\star }_\lambda, \end{cases} \end{equation}
We stress that the Faber–Krahn inequality (3.8) implies that
and hence
![]() $m^\star$
is well defined in
$m^\star$
is well defined in
![]() $\Omega ^\star _\lambda$
.
$\Omega ^\star _\lambda$
.
Let
![]() $z$
be a positive eigenfunction for the problem (4.3) corresponding to the first eigenvalue
$z$
be a positive eigenfunction for the problem (4.3) corresponding to the first eigenvalue
![]() $\lambda ^H_{p,q}(\Omega )$
, and we observe that repeating the same argument as before, by Proposition 3.4, for any
$\lambda ^H_{p,q}(\Omega )$
, and we observe that repeating the same argument as before, by Proposition 3.4, for any
![]() $1\lt q\,{\leqslant}\, p$
we have
$1\lt q\,{\leqslant}\, p$
we have
The following proposition gives a comparison result between the eigenfunctions
![]() $u$
and
$u$
and
![]() $z$
when they are normalized with respect to the
$z$
when they are normalized with respect to the
![]() $L^{\infty }$
norm.
$L^{\infty }$
norm.
Proposition 4.2. Let
![]() $\Omega \subset \mathbb{R}^n$
,
$\Omega \subset \mathbb{R}^n$
,
![]() $n\,{\geqslant}\, 2$
, be an open, bounded, and connected set,
$n\,{\geqslant}\, 2$
, be an open, bounded, and connected set,
![]() $1\lt q\,{\leqslant}\, p$
and let
$1\lt q\,{\leqslant}\, p$
and let
![]() $m\in L^{\infty }(\Omega )$
be a positive function. Let
$m\in L^{\infty }(\Omega )$
be a positive function. Let
![]() $u$
be a positive solution to the problem (1.2) corresponding to
$u$
be a positive solution to the problem (1.2) corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
and let
$\lambda ^H_{p,q}(\Omega )$
and let
![]() $z$
be a positive eigenfunction to the problem (4.3) corresponding to
$z$
be a positive eigenfunction to the problem (4.3) corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
such that
$\lambda ^H_{p,q}(\Omega )$
such that
Then
where
![]() $u^*$
and
$u^*$
and
![]() $z^*$
are, respectively, the decreasing rearrangements of
$z^*$
are, respectively, the decreasing rearrangements of
![]() $u$
and
$u$
and
![]() $z$
. The equality case holds if and only if
$z$
. The equality case holds if and only if
![]() $\Omega =\Omega ^{\star }_\lambda$
and
$\Omega =\Omega ^{\star }_\lambda$
and
![]() $m=m^{\star }$
, that is, in
$m=m^{\star }$
, that is, in
![]() $\Omega$
, up to translations, where
$\Omega$
, up to translations, where
![]() $m^\star$
is the convex symmetrization of
$m^\star$
is the convex symmetrization of
![]() $m$
.
$m$
.
Proof. First of all we stress that, if
![]() $|\Omega |=|\Omega ^\star _\lambda |$
, then there is nothing to prove, since Faber–Krahn inequality implies that
$|\Omega |=|\Omega ^\star _\lambda |$
, then there is nothing to prove, since Faber–Krahn inequality implies that
![]() $u^*(s)=z^*(s)$
.
$u^*(s)=z^*(s)$
.
Moreover, we have
![]() $u^*(|\Omega ^\star _\lambda |)\gt z^*(|\Omega ^\star _\lambda |)=0$
. Then, the following definition is well posed:
$u^*(|\Omega ^\star _\lambda |)\gt z^*(|\Omega ^\star _\lambda |)=0$
. Then, the following definition is well posed:
By definition,
![]() $u^*(s_0)=z^*(s_0)$
, and we want to prove that
$u^*(s_0)=z^*(s_0)$
, and we want to prove that
![]() $s_0=0$
. We proceed by contradiction supposing that
$s_0=0$
. We proceed by contradiction supposing that
![]() $s_0\gt 0$
. Then under this assumption,
$s_0\gt 0$
. Then under this assumption,
![]() $u^*$
and
$u^*$
and
![]() $z^*$
coincide in
$z^*$
coincide in
![]() $0$
and
$0$
and
![]() $s_0$
and we have
$s_0$
and we have
 \begin{equation} \begin{cases} u^*(s)\lt z^*(s) & s\in (0,s_0)\\[5pt] u^*(s)\,{\geqslant}\, z^*(s) & s\in (s_0,|\Omega ^\star _\lambda |). \end{cases} \end{equation}
\begin{equation} \begin{cases} u^*(s)\lt z^*(s) & s\in (0,s_0)\\[5pt] u^*(s)\,{\geqslant}\, z^*(s) & s\in (s_0,|\Omega ^\star _\lambda |). \end{cases} \end{equation}
By (4.1), (4.5), and (4.6), we have that
Integrating between
![]() $(0,s)$
, with
$(0,s)$
, with
![]() $s\in (0,s_0)$
, being
$s\in (0,s_0)$
, being
![]() $u^*(0)=z^*(0)$
, we get
$u^*(0)=z^*(0)$
, we get
which is in contradiction with the definition of
![]() $s_0$
. Hence,
$s_0$
. Hence,
![]() $s_0=0$
, and the proof is completed.
$s_0=0$
, and the proof is completed.
As an immediately consequence of the previous result, we get the following scale-invariant inequality for any
![]() $r\gt 0$
:
$r\gt 0$
:
When the functions
![]() $u$
and
$u$
and
![]() $z$
are normalized with respect to the weighted
$z$
are normalized with respect to the weighted
![]() $L^q$
-norm, we get the following comparison result.
$L^q$
-norm, we get the following comparison result.
Theorem 4.3. Let
![]() $\Omega \subset \mathbb{R}^n$
be an open, bounded, and connected set,
$\Omega \subset \mathbb{R}^n$
be an open, bounded, and connected set,
![]() $1\lt q\,{\leqslant}\, p$
and let
$1\lt q\,{\leqslant}\, p$
and let
![]() $m\in L^{\infty }(\Omega )$
be a positive function. Let
$m\in L^{\infty }(\Omega )$
be a positive function. Let
![]() $u$
be a positive solution to the problem (1.2) corresponding to
$u$
be a positive solution to the problem (1.2) corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
and let
$\lambda ^H_{p,q}(\Omega )$
and let
![]() $z$
be a positive eigenfunction to the problem (4.3) corresponding to
$z$
be a positive eigenfunction to the problem (4.3) corresponding to
![]() $\lambda ^H_{p,q}(\Omega )$
such that
$\lambda ^H_{p,q}(\Omega )$
such that
Then we have
where
![]() $u^*$
,
$u^*$
,
![]() $m^*$
, and
$m^*$
, and
![]() $z^*$
are, respectively, the decreasing rearrangements of
$z^*$
are, respectively, the decreasing rearrangements of
![]() $u$
,
$u$
,
![]() $m$
, and
$m$
, and
![]() $z$
, and
$z$
, and
![]() $m^\star$
is the convex symmetrization of
$m^\star$
is the convex symmetrization of
![]() $m$
. The equality case holds if and only if
$m$
. The equality case holds if and only if
![]() $\Omega =\Omega ^{\star }$
,
$\Omega =\Omega ^{\star }$
,
![]() $z=u=u^*$
, and
$z=u=u^*$
, and
![]() $m=m^{\star }$
, that is,
$m=m^{\star }$
, that is,
![]() $\Omega$
, up to translations.
$\Omega$
, up to translations.
Proof. If
![]() $|\Omega |=|\Omega ^{\star }_\lambda |$
, the conclusion is trivial. Let be
$|\Omega |=|\Omega ^{\star }_\lambda |$
, the conclusion is trivial. Let be
![]() $|\Omega |\gt |\Omega ^{\star }_\lambda |$
, since
$|\Omega |\gt |\Omega ^{\star }_\lambda |$
, since
![]() $u$
and
$u$
and
![]() $z$
verify (4.8), by (4.7) it holds that
$z$
verify (4.8), by (4.7) it holds that
If
![]() $u^*(0)=z^*(0)$
, then Proposition 4.2 and the normalization (4.8) imply that
$u^*(0)=z^*(0)$
, then Proposition 4.2 and the normalization (4.8) imply that
![]() $u^*(s)=z^*(s)$
for every
$u^*(s)=z^*(s)$
for every
![]() $s\in [0,|\Omega ^{\star }_\lambda |]$
and than the claim follows trivially.
$s\in [0,|\Omega ^{\star }_\lambda |]$
and than the claim follows trivially.
Let
![]() $u^*(0)\lt z^*(0)$
. Since
$u^*(0)\lt z^*(0)$
. Since
![]() $u^*(|\Omega ^{\star }_\lambda |)\gt z^*(|\Omega ^{\star }_\lambda |)$
, we can consider
$u^*(|\Omega ^{\star }_\lambda |)\gt z^*(|\Omega ^{\star }_\lambda |)$
, we can consider
Obviously,
![]() $0\lt s_0\lt |\Omega ^{\star }_\lambda |$
,
$0\lt s_0\lt |\Omega ^{\star }_\lambda |$
,
![]() $u^*(s_0)=z^*(s_0)$
and
$u^*(s_0)=z^*(s_0)$
and
![]() $u^*\,{\leqslant}\, z^*$
in
$u^*\,{\leqslant}\, z^*$
in
![]() $[0,s_0]$
. We want to show that
$[0,s_0]$
. We want to show that
![]() $u^*\gt z^*$
in
$u^*\gt z^*$
in
![]() $[s_0,|\Omega ^{\star }_\lambda |]$
. Indeed, if we suppose by contradiction that there exists
$[s_0,|\Omega ^{\star }_\lambda |]$
. Indeed, if we suppose by contradiction that there exists
![]() $s_1\gt s_0$
such that
$s_1\gt s_0$
such that
![]() $u^*(s_1)=z^*(s_1)$
and
$u^*(s_1)=z^*(s_1)$
and
![]() $u^*(s)\gt z^*(s)$
for
$u^*(s)\gt z^*(s)$
for
![]() $s\in (s_0,s_1)$
, we can construct the following function:
$s\in (s_0,s_1)$
, we can construct the following function:
 \begin{equation*} w^*(s)= \begin {cases} z^*(s) & s \in [0,s_0]\cup [s_1,|\Omega ^{\star }_\lambda |]\\[5pt] u^*(s) & s \in [s_0,s_1]. \end {cases} \end{equation*}
\begin{equation*} w^*(s)= \begin {cases} z^*(s) & s \in [0,s_0]\cup [s_1,|\Omega ^{\star }_\lambda |]\\[5pt] u^*(s) & s \in [s_0,s_1]. \end {cases} \end{equation*}
It is straightforward to check that
Applying Coarea Formula and considering the change of variables
![]() $s=k_n t^n$
, we get
$s=k_n t^n$
, we get
Thanks to the normalization (4.8) and the definition of
![]() $w$
, we have that
$w$
, we have that
then by (4.1) and (4.5), we have that
Multiplying (4.10) by
![]() $-w^{\prime }$
, rearranging the terms and integrating between
$-w^{\prime }$
, rearranging the terms and integrating between
![]() $0$
and
$0$
and
![]() $|\Omega ^{\star }_\lambda |$
, we get
$|\Omega ^{\star }_\lambda |$
, we get
 \begin{equation*} \begin {aligned} n^pk_n^{\frac {p}{n}}&\int _0^{|\Omega ^{\star }_\lambda |} s^{p-\frac {p}{n}}(-{w^*}^{\prime }(s))^p\,ds\,{\leqslant}\, \\[5pt] &\,{\leqslant}\, \lambda ^H_{p,q}(\Omega ) \| w^*\|_{q,m^*}^{p-q} \int _0^{|\Omega ^{\star }_\lambda |}(-{w^*}^{\prime }(s))\int _0^sm^*(r)({w^*})^{q-1}(r)\,dr\,ds. \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} n^pk_n^{\frac {p}{n}}&\int _0^{|\Omega ^{\star }_\lambda |} s^{p-\frac {p}{n}}(-{w^*}^{\prime }(s))^p\,ds\,{\leqslant}\, \\[5pt] &\,{\leqslant}\, \lambda ^H_{p,q}(\Omega ) \| w^*\|_{q,m^*}^{p-q} \int _0^{|\Omega ^{\star }_\lambda |}(-{w^*}^{\prime }(s))\int _0^sm^*(r)({w^*})^{q-1}(r)\,dr\,ds. \end {aligned} \end{equation*}
An integration by parts allows us to conclude that
 \begin{equation*} \frac {\displaystyle \int _{\Omega ^\star _\lambda } H(\nabla w)^p\,dx}{\bigg (\displaystyle \int _{\Omega ^\star _\lambda }m^\star w^q\,dx\bigg )^{\frac {p}{q}}}=\frac {\displaystyle n^pk_n^{\frac {p}{n}}\int _0^{|\Omega ^{\star }_\lambda |} s^{p-\frac {p}{n}}(-w^{\prime }(s))^p\,ds}{\bigg (\displaystyle \int _0^{|\Omega ^{\star }_\lambda |}m^*(s)({w^*})^q(s)\,ds\bigg )^{\frac {p}{q}}}\,{\leqslant}\, \lambda ^H_{p,q}(\Omega )=\lambda ^H_{p,q}(\Omega ^{\star }_\lambda ). \end{equation*}
\begin{equation*} \frac {\displaystyle \int _{\Omega ^\star _\lambda } H(\nabla w)^p\,dx}{\bigg (\displaystyle \int _{\Omega ^\star _\lambda }m^\star w^q\,dx\bigg )^{\frac {p}{q}}}=\frac {\displaystyle n^pk_n^{\frac {p}{n}}\int _0^{|\Omega ^{\star }_\lambda |} s^{p-\frac {p}{n}}(-w^{\prime }(s))^p\,ds}{\bigg (\displaystyle \int _0^{|\Omega ^{\star }_\lambda |}m^*(s)({w^*})^q(s)\,ds\bigg )^{\frac {p}{q}}}\,{\leqslant}\, \lambda ^H_{p,q}(\Omega )=\lambda ^H_{p,q}(\Omega ^{\star }_\lambda ). \end{equation*}
By the minimality and the simplicity of
![]() $\lambda ^H_{p,q}$
, and the definition of
$\lambda ^H_{p,q}$
, and the definition of
![]() $w^*$
, it must be
$w^*$
, it must be
![]() $w^*(s)=z^*(s)$
for every
$w^*(s)=z^*(s)$
for every
![]() $s\in [0,|\Omega ^{\star }_\lambda |]$
, but this is a contradiction since in
$s\in [0,|\Omega ^{\star }_\lambda |]$
, but this is a contradiction since in
![]() $(s_0,s_1)$
we have that
$(s_0,s_1)$
we have that
![]() $u^*(s)\gt z^*(s)$
.
$u^*(s)\gt z^*(s)$
.
In this way, we have proved that there exists a unique point
![]() $s_0$
where
$s_0$
where
![]() $u^*$
and
$u^*$
and
![]() $z^*$
can cross each other, and such that
$z^*$
can cross each other, and such that
 \begin{equation} \begin{cases} u^*(s)\,{\leqslant}\, z^*(s) & s\in [0,s_0]\\[5pt] u^*(s)\,{\geqslant}\, z^*(s) & s\in [s_0,|\Omega ^{\star }_\lambda |]. \end{cases} \end{equation}
\begin{equation} \begin{cases} u^*(s)\,{\leqslant}\, z^*(s) & s\in [0,s_0]\\[5pt] u^*(s)\,{\geqslant}\, z^*(s) & s\in [s_0,|\Omega ^{\star }_\lambda |]. \end{cases} \end{equation}
If we extend
![]() $z^*$
to be zero in
$z^*$
to be zero in
![]() $[|\Omega ^{\star }_\lambda |, |\Omega |]$
, by (4.8) and (4.11) then we have that for every
$[|\Omega ^{\star }_\lambda |, |\Omega |]$
, by (4.8) and (4.11) then we have that for every
![]() $s\in [0,|\Omega |]$
$s\in [0,|\Omega |]$
Indeed (4.11) implies that the function:
has a maximum in
![]() $s_0$
and cannot be negative in any point. This proves (4.12). Finally, inequality (4.9) follows easily by (4.12) by using Proposition 2.4 being
$s_0$
and cannot be negative in any point. This proves (4.12). Finally, inequality (4.9) follows easily by (4.12) by using Proposition 2.4 being
![]() $m^{\star }(u^{\star })^q \prec m^{\star }z^q$
.
$m^{\star }(u^{\star })^q \prec m^{\star }z^q$
.
Proof of Theorem 1.1. The proof of statement i) follows directly from (4.8) and (4.9), indeed we have
 \begin{equation*} \bigg (\int _{\Omega } m u^{r}\,dx\bigg )^{\frac {1}{r}}\,{\leqslant}\, \bigg (\int _{\Omega ^{\star }_\lambda } m^\star z^{r}\,dx\bigg )^{\frac {1}{r}} = \frac {\displaystyle \bigg (\int _{\Omega ^{\star }_\lambda } m^\star z^{r}\,dx\bigg )^{\frac {1}{r}} }{\displaystyle \bigg (\int _{\Omega ^{\star }_\lambda } m^\star z^{q}\,dx\bigg )^{\frac {1}{q}} } \bigg (\int _{\Omega } m u^{q}\,dx\bigg )^{\frac {1}{q}}. \end{equation*}
\begin{equation*} \bigg (\int _{\Omega } m u^{r}\,dx\bigg )^{\frac {1}{r}}\,{\leqslant}\, \bigg (\int _{\Omega ^{\star }_\lambda } m^\star z^{r}\,dx\bigg )^{\frac {1}{r}} = \frac {\displaystyle \bigg (\int _{\Omega ^{\star }_\lambda } m^\star z^{r}\,dx\bigg )^{\frac {1}{r}} }{\displaystyle \bigg (\int _{\Omega ^{\star }_\lambda } m^\star z^{q}\,dx\bigg )^{\frac {1}{q}} } \bigg (\int _{\Omega } m u^{q}\,dx\bigg )^{\frac {1}{q}}. \end{equation*}
Therefore, we have
with
The proof of statement ii) follows immediately by Proposition 4.2 with
![]() $C= \frac{\|z\|_{\infty }}{\|z\|_{L^r(\Omega ^\star, m^\star )}}$
and the theorem is completely proved.
$C= \frac{\|z\|_{\infty }}{\|z\|_{L^r(\Omega ^\star, m^\star )}}$
and the theorem is completely proved.
Acknowledgments
This work has been partially supported by MiUR PRIN 2017 grant “Qualitative and quantitative aspects of nonlinear PDEs,” the MiUR PRIN-PNRR 2022 grant “Linear and Nonlinear PDE’s: New directions and Applications,” and GNAMPA of INdAM. The second author acknowledges the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Pisa, CUP I57G22000700001.
Conflicts of interest
The authors declare that there is no conflict of interest.
Data availability statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.