Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-10T00:50:36.568Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Jacobson's conjecture for right Noetherian rings

Published online by Cambridge University Press:  18 May 2009

K. A. Brown  and
T. H. Lenagan
K. A. Brown
Affiliation:
University of Glasgow
T. H. Lenagan
Affiliation:
University of Edinburgh
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1956, Jacobson asked whether the intersection of the powers of the Jacobson radical, J(R), of a right Noetherian ring R, must always be zero [4, p. 200]. His question was answered in the negative by I. N. Herstein [3], who noted that 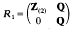, where Z(2) denotes the ring of rational numbers with denominator prime to 2, affords a counterexample. In contrast, the ring 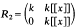, though similar in appearance to R1, satisfies 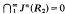. (Here, k denotes a field.)

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 23 , Issue 1 , January 1982 , pp. 7 - 8
Copyright
Copyright © Glasgow Mathematical Journal Trust 1982

References

REFERENCES

1.Chatters, A. W., Goldie, A. W., Hajarnavis, C. R. and Lenagan, T. H., Reduced rank in Noetherian rings, J. Algebra 61 (1979), 582–589.CrossRefGoogle Scholar
2.Eisenbud, D., Subrings of Artinian and Noetherian rings, Math. Ann. 185 (1970), 247–249.CrossRefGoogle Scholar
3.Herstein, I. N., A counterexample in Noetherian rings, Proc. Nat. Acad. Sc. U.S.A. 54 (1965), 1036–1037.CrossRefGoogle ScholarPubMed
4.Jacobson, N., Structure of rings (Colloq. Publications 37, Amer. Math. Soc, Providence, 1956).CrossRefGoogle Scholar
5.Procesi, C., Rings with polynomial identities (Dekker, 1973).Google Scholar
6.Rosenberg, A. and Zelinsky, D., Finiteness of the injective hull, Math. Z. 70 (1959), 372–380.CrossRefGoogle Scholar