Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T21:37:42.540Z Has data issue: false hasContentIssue false
  • English
  • Français

MODULES WITH FI-EXTENDING HULLS

Published online by Cambridge University Press:  01 May 2009

GARY F. BIRKENMEIER ,
JAE KEOL PARK  and
S. TARIQ RIZVI
GARY F. BIRKENMEIER
Affiliation:
Department of Mathematics, University of Louisiana at Lafayette, Lafayette, LA 70504-1010, USA e-mail: [email protected]
JAE KEOL PARK
Affiliation:
Department of Mathematics, Busan National University, Busan 609-735, South Korea e-mail: [email protected]
S. TARIQ RIZVI
Affiliation:
Department of Mathematics, Ohio State University, Lima, OH 45804-3576, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that every finitely generated projective module PR over a semiprime ring R has the smallest FI-extending essential module extension 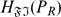(called the absolute FI-extending hull of PR) in a fixed injective hull of PR. This module hull is explicitly described. It is proved that 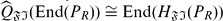, where 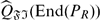is the smallest right FI-extending right ring of quotients of End(PR) (in a fixed maximal right ring of quotients of End(PR). Moreover, we show that a finitely generated projective module PR over a semiprime ring R is FI-extending if and only if it is a quasi-Baer module and if and only if End(PR) is a quasi-Baer ring. An application of this result to C*-algebras is considered. Various examples which illustrate and delimit the results of this paper are provided.

Keywords

Primary 16N6016D40Secondary 16S50
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 2 , May 2009 , pp. 347 - 357
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Ara, P., The extended centroid of C*-algebras Arch. Math. 54 (1990), 358–364.CrossRefGoogle Scholar
2.Ara, P., On the symmetric algebra of quotients of a C*-algebra, Glasgow Math. J. 32 (1990), 377–379.CrossRefGoogle Scholar
3.Ara, P. and Mathieu, M., A local version of the Dauns–Hofmann theorem, Math. Z. 208 (1991), 349–353.CrossRefGoogle Scholar
4.Ara, P. and Mathieu, M., An application of local multipliers to centralizing mappings of C*-algebras, Quart. J. Math. Oxford 44 (1993), 129–138.CrossRefGoogle Scholar
5.Ara, P. and Mathieu, M., Local multipliers of C*-algebras (Springer, Berlin, Germany, 2003).CrossRefGoogle Scholar
6.Azoff, E. A., Kaplansky–Hilbert modules and the self-adjointness of operator algebras, Am. J. Math. 100 (1978), 957–972.CrossRefGoogle Scholar
7.Birkenmeier, G. F., A generalization of FPF rings, Comm. Algebra 17 (1989), 855–884.CrossRefGoogle Scholar
8.Birkenmeier, G. F., Decomposition of Baer-like rings, Acta Math. Hungar. 59 (1992), 319–326.CrossRefGoogle Scholar
9.Birkenmeier, G. F., When does a supernilpotent radical essentially split-off? J. Algebra 172 (1995), 49–60.CrossRefGoogle Scholar
10.Birkenmeier, G. F., Călugăreanu, G., Fuchs, L. and Goeters, H. P., The fully invariant extending property for Abelian groups, Comm. Algebra 29 (2001), 673–685.CrossRefGoogle Scholar
11.Birkenmeier, G. F., Kim, J. Y. and Park, J. K., On quasi-Baer rings, in Algebra and its applications (Huynh, D. V., Jain, S. K. and López-Permouth, S. R., Editors)(Amer. Math. Soc., Providence, RI, 2000), 67–92.CrossRefGoogle Scholar
12.Birkenmeier, G. F., Müller, B. J. and Rizvi, S. T., Modules in which every fully invariant submodule is essential in a direct summand, Comm. Algebra 30 (2002), 1395–1415.CrossRefGoogle Scholar
13.Birkenmeier, G. F. and Park, J. K., Triangular matrix representations of ring extensions, J. Algebra 265 (2003), 457–477.CrossRefGoogle Scholar
14.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., Generalized triangular matrix rings and the fully invariant extending property, Rocky Mountain J. Math. 32 (2002), 1299–1319.CrossRefGoogle Scholar
15.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., Modules with fully invariant submodules essential in fully invariant summands, Comm. Algebra 30 (2002), 1833–1852.CrossRefGoogle Scholar
16.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., An essential extension with nonisomorphic ring structures, Algebra and its applications (Huynh, D. V., Jain, S. K. and López-Permouth, S. R., Editors) (Amer. Math. Soc., Providence, RI, 2006), 29–48.CrossRefGoogle Scholar
17.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., Ring hulls and applications, J. Algebra 304 (2006), 633–665.CrossRefGoogle Scholar
18.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., Hulls of ring extensions, Canad. Math. Bull. (in press).Google Scholar
19.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., Hulls of semiprime rings with applications to C*-algebras, J. Algebra (in press).Google Scholar
20.Blecher, D. P. and Le Merdy, C., Operator algebras and their modules – An operator space approach (Clarendon, Oxford, 2004).Google Scholar
21.Chatters, A. W. and Hajarnavis, C. R., Rings in which every complement right ideal is a direct summand, Quart. J. Math. Oxford 28 (1977), 61–80.CrossRefGoogle Scholar
22.Clark, W. E., Twisted matrix units semigroup algebras, Duke Math. J. 34 (1967), 417–424.CrossRefGoogle Scholar
23.Dung, N. V., Huynh, D. V., Smith, P. F. and Wisbauer, R., Extending Modules (Longman, Harlow, 1994).Google Scholar
24.Elliott, G. A., Automorphisms determined by multipliers on ideals of a C*-algebra, J. Funct. Anal. 23 (1976), 1–10.CrossRefGoogle Scholar
25.Faith, C., Rings with ascending condition on annihilators, Nagoya Math. J. 27 (1966), 179–191.CrossRefGoogle Scholar
26.Grabiner, S., Finitely generated, Noetherian, and Artinian Banach modules, Indiana Univ. Math. J. 26 (1977), 413–425.CrossRefGoogle Scholar
27.Jin, H. L., Doh, J. and Park, J. K., Group actions on quasi-Baer rings, Canad. Math. Bull. (in press).Google Scholar
28.Kaplansky, I., Modules over operator algebras, Am. J. Math. 75 (1953), 839–858.CrossRefGoogle Scholar
29.Kaplansky, I., Rings of operators (Benjamin, New York, 1968).Google Scholar
30.Lam, T. Y., Lectures on Modules and Rings (Springer-Verlag, Berlin, Germany, 1998).Google Scholar
31.Lambek, J., Lectures on rings and modules (Chelsea, New York, 1986).Google Scholar
32.Mewborn, A. C., Regular rings and Baer rings, Math. Z. 121 (1971), 211–219.CrossRefGoogle Scholar
33.Müller, B. J. and Rizvi, S. T., Ring decompositions of CS-rings, in Abstracts for methods in module theory conference (Colorado Springs, May 1991).Google Scholar
34.Osofsky, B. L., A non-trivial ring with non-rational injective hull, Canad. Math. Bull. 10 (1967), 275–282.Google Scholar
35.Pedersen, G. K., Approximating derivations on ideals of C*-algebras, Invent. Math. 45 (1978), 299–305.CrossRefGoogle Scholar
36.Pollingher, A. and Zaks, A., On Baer and quasi-Baer rings, Duke Math. J. 37 (1970), 127–138.CrossRefGoogle Scholar
37.Rizvi, S. T. and Roman, C. S., Baer and quasi-Baer modules, Comm. Algebra 32 (2004), 103–123.CrossRefGoogle Scholar