Article contents
Kurosh's chains of associative rings
Published online by Cambridge University Press: 18 May 2009
Extract
Let N be a homomorphically closed class of associative rings. Put N1 = Nl = N and, for ordinals a ≥ 2, define Nα (Nα) to be the class of all associative rings R such that every non-zero homomorphic image of R contains a non-zero ideal (left ideal) in Nβ for some β<α. In this way we obtain a chain {Nα} ({Nα}), the union of which is equal to the lower radical class IN (lower left strong radical class IsN) determined by N. The chain {Nα} is called Kurosh's chain of N. Suliński, Anderson and Divinsky proved [7] that 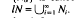 . Heinicke [3] constructed an example of N for which lN ≠ Nk for k = 1, 2,. … In [1] Beidar solved the main problem in the area showing that for every natural number n ≥ 1 there exists a class N such that IN = Nn+l ≠ Nn. Some results concerning the termination of the chain {Nα} were obtained in [2,4]. In this paper we present some classes N with Nα = Nα for all α Using this and Beidar's example we prove that for every natural number n ≥ 1 there exists an N such that Nα = Nα for all α and Nn ≠ Nn+i = Nn+2. This in particular answers Question 6 of [4].
. Heinicke [3] constructed an example of N for which lN ≠ Nk for k = 1, 2,. … In [1] Beidar solved the main problem in the area showing that for every natural number n ≥ 1 there exists a class N such that IN = Nn+l ≠ Nn. Some results concerning the termination of the chain {Nα} were obtained in [2,4]. In this paper we present some classes N with Nα = Nα for all α Using this and Beidar's example we prove that for every natural number n ≥ 1 there exists an N such that Nα = Nα for all α and Nn ≠ Nn+i = Nn+2. This in particular answers Question 6 of [4].
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1990
References
REFERENCES
- 4
- Cited by


