Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T07:48:00.111Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES

Part of: Special classes of linear operators Integral, integro-differential, and pseudodifferential operators Integral transforms, operational calculus

Published online by Cambridge University Press:  28 January 2018

THOMAS VILS PEDERSEN Open the ORCID record for THOMAS VILS PEDERSEN [Opens in a new window]
THOMAS VILS PEDERSEN*
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen Ø, Denmark e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize those non-negative, measurable functions ψ on [0, 1] and positive, continuous functions ω1 and ω2 on ℝ+ for which the generalized Hardy–Cesàro operator

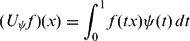$$\begin{equation*}(U_{\psi}f)(x)=\int_0^1 f(tx)\psi(t)\,dt\end{equation*}$$
defines a bounded operator Uψ: L1(ω1) → L1(ω2) This generalizes a result of Xiao [7] to weighted spaces. Furthermore, we extend Uψ to a bounded operator on M(ω1) with range in L1(ω2) ⊕ ℂδ0, where M(ω1) is the weighted space of locally finite, complex Borel measures on ℝ+. Finally, we show that the zero operator is the only weakly compact generalized Hardy–Cesàro operator from L1(ω1) to L1(ω2).

MSC classification

Primary: 44A15: Special transforms (Legendre, Hilbert, etc.)
Secondary: 47B34: Kernel operators 47B38: Operators on function spaces (general) 47G10: Integral operators
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 1 , January 2019 , pp. 13 - 24
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Albanese, A. A., Bonet, J. and Ricker, W. J., On the continuous Cesàro operator in certain function spaces, Positivity. 19 (2015), 659–679.Google Scholar
2. Albanese, A. A., Bonet, J. and Ricker, W. J., Spectrum and compactness of the Cesàro operator on weighted lp spaces, J. Aust. Math. Soc. 99 (2015), 287–314.Google Scholar
3. Bradley, J. S., Hardy inequalities with mixed norms, Canad. Math. Bull. 21 (1978), 405–408.Google Scholar
4. Dunford, N. and Schwartz, J. T., Linear operators, part I (Interscience, New York, 1958).Google Scholar
5. Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities 2nd edition (Cambridge University Press, London, 1952).Google Scholar
6. Muckenhoupt, B., Hardy's inequality with weights, Studia Math. 44 (1972), 31–38.Google Scholar
7. Xiao, J., Lp and BMO bounds of weighted Hardy-Littlewood averages, J. Math. Anal. Appl. 262 (2001), 660–666.Google Scholar