Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-23T18:55:46.696Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite groups generated by subnormal T-subgroups

Published online by Cambridge University Press:  18 May 2009

John Cossey
John Cossey
Affiliation:
Department of Mathematics, Australian National University, The Faculties, Canberra ACT 0200, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our aim in this paper is to investigate the restrictions placed on the structure of a finite group if it can be generated by subnormal T-subgroups (a T-group is a group in which every subnormal subgroup is normal). For notational convenience we denote by 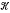the class of finite groups that can be generated by subnormal T-subgroups and by 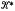the subclass of 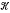of those finite groups generated by normal T-subgroups; and for the remainder of this paper we will only consider finite groups.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 37 , Issue 3 , September 1995 , pp. 363 - 371
Copyright
Copyright © Glasgow Mathematical Journal Trust 1995

References

REFERENCES

1.Aschbacher, M., Finite group theory (Cambridge studies in advanced mathematics 10, Cambridge University Press, Cambridge, 1986).Google Scholar
2.Bryce, R. A. and Cossey, John, The Wielandt subgroup of a finite soluble group, J. London Math. Soc. (2) 40 (1989) 244–256.CrossRefGoogle Scholar
3.Cossey, John, Finite insoluble T-groups, in preparation.Google Scholar
4.Curtis, Charles W. and Reiner, Irving, Representation theory of finite groups and associative algebras (Interscience Publishers, 1962).Google Scholar
5.Hall, Marshall Jr, The theory of groups (Macmillan 1959).Google Scholar
6.Higman, G., Complementation of abelian normal subgroups, Publ. Math. Debrecen 4 (1955–1956) 455–458.CrossRefGoogle Scholar
7.Huppert, B., Endliche Gruppen I, Die Grundlehren der mathematischen Wissenschaften Bd 134 (Springer Verlag, 1967).CrossRefGoogle Scholar
8.Huppert, B. and Blackburn, N., Finite groups III, Grundlehren der mathematischen Wissenschaften Bd 243 (Springer Verlag, 1982).Google Scholar
9.Lennox, John C. and Stonehewer, Stewart E., Subnormal subgroups of groups (Oxford mathematical monographs, Oxford University Press, 1987).Google Scholar
10.Marconi, Riccardo, Sulla classe di nilpotenza dei prodotti intrecciati, Boll. Un. Mat. Ital. D (6) 2 (1983) 9–20.Google Scholar
11.Ormerod, Elizabeth, The Wielandt subgroup of a metacyclic p-group, Bull. Austral. Math. Soc. 42 (1990) 499–510.CrossRefGoogle Scholar
12.Robinson, D. J. S., A course in the theory of groups (Springer Verlag, 1980).Google Scholar