Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chakraborty, K.
Hoque, A.
Kishi, Y.
and
Pandey, P.P.
2018.
Divisibility of the class numbers of imaginary quadratic fields.
Journal of Number Theory,
Vol. 185,
Issue. ,
p.
339.
Kim, Kwang-Seob
2022.
Some Remarks on the Divisibility of the Class Numbers of Imaginary Quadratic Fields.
Mathematics,
Vol. 10,
Issue. 14,
p.
2488.
Kim, Kwang-Seob
and
König, Joachim
2024.
On -unramified extensions over imaginary quadratic fields.
Glasgow Mathematical Journal,
Vol. 66,
Issue. 1,
p.
119.
Ram, Mahesh Kumar
2024.
Determination of all imaginary cyclic quartic fields of prime class number p ≡ 3(mod4), and non-divisibility of class numbers.
International Journal of Number Theory,
Vol. 20,
Issue. 03,
p.
811.
Agnihotri, Rishabh
Laishram, Shanta
and
Mishra, Mohit
2025.
On the class number of $${\mathbb {Q}}(\sqrt{(2^ra)^{2}- y^p})$$.
The Ramanujan Journal,
Vol. 66,
Issue. 1,
Jin, Seokho
and
Kim, Kwang-Seob
2025.
A new family of imaginary quadratic fields with class number divisible by 5.
The Ramanujan Journal,
Vol. 66,
Issue. 3,


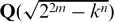
 ∣
∣ 