Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-03T19:57:33.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Computer generated natural inner automorphisms of Cayley's algebra

Published online by Cambridge University Press:  18 May 2009

P. J. C. Lamont
P. J. C. Lamont
Affiliation:
QIS Department, Western Illinois University Macomb, Illinois 61455
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper results from the design and development of computer software for lengthy computations with Cayley's algebra C over the field of reals. The algebra C is 8-dimensional over the reals and is not associative. Integer elements of C are defined and can be stored as integer arrays. The problem of solving linear equations αξ = β in C is implemented by using the equation 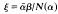where 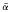is the conjugate and N(α) is the non-zero norm of α. Programming multiplication of Cayley numbers is comparable in difficulty to programming matrix multiplication for matrices with eight rows and eight columns.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 23 , Issue 2 , July 1982 , pp. 187 - 189
Copyright
Copyright © Glasgow Mathematical Journal Trust 1982

References

REFERENCES

1.Bunch, J. R. and Rose, D. J., Sparse matrix computations (New York, 1976).Google Scholar
2.Jacobson, N., Composition algebras and their automorphisms, Rend. Circ. Mat. Palermo 7 (1958), 55–80.CrossRefGoogle Scholar
3.Lamont, P. J. C., Arithmetics in Cayley's algebra, Proc. Glasgow Math. Assoc. 6 (1963), 99–106.CrossRefGoogle Scholar
4.Lamont, P. J. C., Factorization and arithmetic functions for orders in composition algebras, Glasgow Math. J. 14 (1973), 86–95.CrossRefGoogle Scholar