Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-03T19:49:54.731Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of spectral operators on Hilbert spaces

Published online by Cambridge University Press:  18 May 2009

Ernst Albrecht
Ernst Albrecht
Affiliation:
Fachbereich Mathematik, Universität des Saarlandes, D-6600 Saarbrücken
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a complex Hilbert space and denote by B(H) the Banach algebra of all bounded linear operators on H. In [5; 6] J. Ph. Labrousse proved that every operator S∈B(H) which is spectral in the sense of N. Dunford (see [3]) is similar to a T∈B(H) with the following property

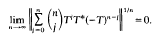
Conversely, he showed that given an operator S∈B(H) such that its essential spectrum (in the sense of [5; 6]) consists of at most one point and such that S is similar to a T∈B(H) with the property (1), then S is a spectral operator. This led him to the conjecture that an operator S∈B(H) is spectral if and only if it is similar to a T∈B(H) with property (1). The purpose of this note is to prove this conjecture in the case of operators which are decomposable in the sense of C. Foias (see [2]).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 23 , Issue 1 , January 1982 , pp. 91 - 95
Copyright
Copyright © Glasgow Mathematical Journal Trust 1982

References

REFERENCES

1.Albrecht, E., On decomposable operators, Integral Equations and Operator Theory, 2 (1979), 1–10.CrossRefGoogle Scholar
2.Colojoară, I. and Foiaş, C., Theory of generalized spectral operators (Gordon and Breach, New York, 1968).Google Scholar
3.Dunford, N. and Schwartz, J., Linear operators, Part III: Spectral operators (Wiley-Interscience, New York, 1971).Google Scholar
4.Hurewicz, W. and Wallman, H., Dimension theory (Princeton University Press, 1948).Google Scholar
5.Labrousse, J.-Ph., Opérateurs spectraux et operateurs quasi normaux. C.R. Acad. Sc. Paris, 286 (1978), 1107–1108.Google Scholar
6.Labrousse, J.-Ph., Les opérateurs quasi Fredholm: Une généralisation des opérateurs semi Fredholm (I.M.S.P. Mathématiques, Nice Cedex, 1978).Google Scholar
7.Lange, R., On generalization of decomposability, Glasgow Math. J. 22 (1981), 77–81.CrossRefGoogle Scholar
8.Nagy, B., Operators with the spectral decomposition property are decomposable (preprint).Google Scholar