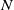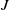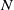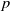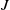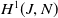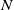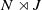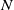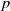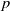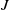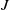1. Introduction
Given a finite nilpotent group
![]() $J$
acting on a finite nilpotent group
$J$
acting on a finite nilpotent group
![]() $N$
via automorphisms, crossed homomorphisms are maps
$N$
via automorphisms, crossed homomorphisms are maps
![]() $\varphi \,:\, J \to N$
satisfying
$\varphi \,:\, J \to N$
satisfying
![]() $\varphi (\,jj^{\prime}) = \varphi (\,j) \varphi (\,j^{\prime})^{j^{-1}}$
for all
$\varphi (\,jj^{\prime}) = \varphi (\,j) \varphi (\,j^{\prime})^{j^{-1}}$
for all
![]() $j,\,j^{\prime} \in J$
. Two such maps
$j,\,j^{\prime} \in J$
. Two such maps
![]() $\varphi$
and
$\varphi$
and
![]() $\varphi ^{\prime}$
are cohomologous if there exists
$\varphi ^{\prime}$
are cohomologous if there exists
![]() $n \in N$
such that
$n \in N$
such that
![]() $\varphi ^{\prime}(\,j) = n^{-1} \varphi (\,j) n^{j^{-1}}$
for all
$\varphi ^{\prime}(\,j) = n^{-1} \varphi (\,j) n^{j^{-1}}$
for all
![]() $j\in J$
; in this case, we write
$j\in J$
; in this case, we write
![]() $\varphi \sim \varphi ^{\prime}$
. We define the first cohomology
$\varphi \sim \varphi ^{\prime}$
. We define the first cohomology
![]() $H^1(J,N)$
to be the pointed set
$H^1(J,N)$
to be the pointed set
![]() $Z^1(J,N)$
of crossed homomorphisms modulo this equivalence relation where the distinguished point corresponds to the class containing the map taking each element of
$Z^1(J,N)$
of crossed homomorphisms modulo this equivalence relation where the distinguished point corresponds to the class containing the map taking each element of
![]() $J$
to the identity of
$J$
to the identity of
![]() $N$
.
$N$
.
We first show that the cohomology set
![]() $H^1(J,N)$
decomposes in terms of the first cohomologies of the Sylow
$H^1(J,N)$
decomposes in terms of the first cohomologies of the Sylow
![]() $p$
-subgroups
$p$
-subgroups
![]() $J_p$
of
$J_p$
of
![]() $J$
as follows:
$J$
as follows:
Lemma 1.
For finite nilpotent groups
![]() $J$
and
$J$
and
![]() $N$
, suppose
$N$
, suppose
![]() $J$
acts on
$J$
acts on
![]() $N$
via automorphisms. Then the map
$N$
via automorphisms. Then the map
![]() $\varphi \mapsto \times _{p\in \mathcal {D}} \varphi |_{J_p}$
for
$\varphi \mapsto \times _{p\in \mathcal {D}} \varphi |_{J_p}$
for
![]() $\varphi \in H^1(J,N)$
induces an isomorphism
$\varphi \in H^1(J,N)$
induces an isomorphism
![]() $H^1(J,N) \cong \times _{p\in \mathcal {D}} H^1(J_p, N)^{J_p^{\prime}}$
of pointed sets, where
$H^1(J,N) \cong \times _{p\in \mathcal {D}} H^1(J_p, N)^{J_p^{\prime}}$
of pointed sets, where
![]() $\mathcal D$
denotes the shared prime divisors of
$\mathcal D$
denotes the shared prime divisors of
![]() $\lvert J\rvert$
and
$\lvert J\rvert$
and
![]() $\lvert N\rvert$
, and for each
$\lvert N\rvert$
, and for each
![]() $p$
,
$p$
,
![]() $J_p$
is the Sylow
$J_p$
is the Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $J$
and
$J$
and
![]() $J_p^{\prime}$
is the Hall
$J_p^{\prime}$
is the Hall
![]() $p^{\prime}$
-subgroup of
$p^{\prime}$
-subgroup of
![]() $J$
.
$J$
.
This parallels the well-known primary decomposition of
![]() $H^1(J,N)$
for abelian
$H^1(J,N)$
for abelian
![]() $N$
(see Section 3 for details). As the bijective correspondence between
$N$
(see Section 3 for details). As the bijective correspondence between
![]() $H^1(J,N)$
and the
$H^1(J,N)$
and the
![]() $N$
-conjugacy classes of complements to
$N$
-conjugacy classes of complements to
![]() $N$
in
$N$
in
![]() $N\rtimes J$
continues to hold for nonabelian
$N\rtimes J$
continues to hold for nonabelian
![]() $N$
[Reference Serre6, Exer. 1 in §I.5.1], Lemma1 provides an alternate proof of a result of Losey and Stonehewer [Reference Losey and Stonehewer5]:
$N$
[Reference Serre6, Exer. 1 in §I.5.1], Lemma1 provides an alternate proof of a result of Losey and Stonehewer [Reference Losey and Stonehewer5]:
Proposition 2 (Losey and Stonehewer). Two nilpotent complements of a normal nilpotent subgroup in a finite group are conjugate if and only if they are locally conjugate.
Here, two subgroups
![]() $H, H^{\prime}\leq G$
are locally conjugate if a Sylow
$H, H^{\prime}\leq G$
are locally conjugate if a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $H$
is conjugate to a Sylow
$H$
is conjugate to a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $H^{\prime}$
for each prime
$H^{\prime}$
for each prime
![]() $p$
. It also readily follows that:
$p$
. It also readily follows that:
Proposition 3.
Let
![]() $G$
be a finite split extension over a nilpotent subgroup
$G$
be a finite split extension over a nilpotent subgroup
![]() $N$
such that
$N$
such that
![]() $G/N$
is nilpotent. If for each prime
$G/N$
is nilpotent. If for each prime
![]() $p$
, there is a Sylow
$p$
, there is a Sylow
![]() $p$
-subgroup
$p$
-subgroup
![]() $S$
of
$S$
of
![]() $G$
such that any two complements of
$G$
such that any two complements of
![]() $S\cap N$
in
$S\cap N$
in
![]() $S$
are conjugate in
$S$
are conjugate in
![]() $G$
, then any two complements of
$G$
, then any two complements of
![]() $N$
in
$N$
in
![]() $G$
are conjugate.
$G$
are conjugate.
We then establish a fixed point result for nilpotent-by-nilpotent actions in the style of Glauberman:
Theorem 4.
For finite nilpotent groups
![]() $J$
and
$J$
and
![]() $N$
, suppose
$N$
, suppose
![]() $J$
acts on
$J$
acts on
![]() $N$
via automorphisms and that the induced semidirect product
$N$
via automorphisms and that the induced semidirect product
![]() $N\rtimes J$
acts on some non-empty set
$N\rtimes J$
acts on some non-empty set
![]() $\Omega$
where the action of
$\Omega$
where the action of
![]() $N$
is transitive. If for each prime
$N$
is transitive. If for each prime
![]() $p$
, a Sylow
$p$
, a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $J$
fixes an element of
$J$
fixes an element of
![]() $\Omega$
, then
$\Omega$
, then
![]() $J$
fixes an element of
$J$
fixes an element of
![]() $\Omega$
.
$\Omega$
.
Glauberman showed that this result holds whenever the orders of
![]() $N$
and
$N$
and
![]() $J$
are coprime, without any further restrictions on
$J$
are coprime, without any further restrictions on
![]() $N$
or
$N$
or
![]() $J$
[Reference Glauberman4, Thm. 4]. Thus, this result is only interesting when
$J$
[Reference Glauberman4, Thm. 4]. Thus, this result is only interesting when
![]() $\lvert N\rvert$
and
$\lvert N\rvert$
and
![]() $\lvert J\rvert$
share one or more prime divisors (i.e. when the action is non-coprime). Analogous results hold if
$\lvert J\rvert$
share one or more prime divisors (i.e. when the action is non-coprime). Analogous results hold if
![]() $N$
is abelian or if
$N$
is abelian or if
![]() $N$
is nilpotent and
$N$
is nilpotent and
![]() $N\rtimes J$
is supersoluble [Reference Burkhart2].
$N\rtimes J$
is supersoluble [Reference Burkhart2].
1.1. Outline
In the remainder of this section, we introduce some notation. We then prove the results in Section 2 and conclude in Section 3.
1.2. Notation
All groups in this note are finite. For a nilpotent group
![]() $J$
, we let
$J$
, we let
![]() $J_p\in \textrm {Syl}_p(J)$
denote its unique Sylow
$J_p\in \textrm {Syl}_p(J)$
denote its unique Sylow
![]() $p$
-subgroup and
$p$
-subgroup and
![]() $J_p^{\prime}$
denote its Hall
$J_p^{\prime}$
denote its Hall
![]() $p^{\prime}$
-subgroup so that
$p^{\prime}$
-subgroup so that
![]() $J \cong J_p \times J_p^{\prime}$
. We let
$J \cong J_p \times J_p^{\prime}$
. We let
![]() $g^\gamma =\gamma ^{-1}g\gamma$
for
$g^\gamma =\gamma ^{-1}g\gamma$
for
![]() $g,\gamma \in G$
. We otherwise use standard notation from group theory that can be found in Doerk and Hawkes [Reference Doerk and Hawkes3].
$g,\gamma \in G$
. We otherwise use standard notation from group theory that can be found in Doerk and Hawkes [Reference Doerk and Hawkes3].
For a subgroup
![]() $K\leq J$
, we let
$K\leq J$
, we let
![]() $\varphi |_{K}$
denote the restriction of
$\varphi |_{K}$
denote the restriction of
![]() $\varphi \in Z^1(J,N)$
to
$\varphi \in Z^1(J,N)$
to
![]() $K$
and let
$K$
and let
![]() $\textrm {res}^J_K \,:\, H^1(J,N) \to H^1(K,N)$
be the map induced in cohomology. For
$\textrm {res}^J_K \,:\, H^1(J,N) \to H^1(K,N)$
be the map induced in cohomology. For
![]() $\varphi \in Z^1(K,N)$
and
$\varphi \in Z^1(K,N)$
and
![]() $j\in J$
, define
$j\in J$
, define
![]() $\varphi ^j(x) = \varphi (x^{j^{-1}})^{j}$
. We say
$\varphi ^j(x) = \varphi (x^{j^{-1}})^{j}$
. We say
![]() $\varphi$
is
$\varphi$
is
![]() $J$
-invariant if
$J$
-invariant if
![]() $\textrm {res}^K_{K\cap K^j} \varphi \sim \textrm {res}^{K^j}_{K\cap K^j} \varphi ^j$
for all
$\textrm {res}^K_{K\cap K^j} \varphi \sim \textrm {res}^{K^j}_{K\cap K^j} \varphi ^j$
for all
![]() $j\in J$
and let
$j\in J$
and let
![]() $\textrm {inv}_J H^1(K,N)$
be the set of
$\textrm {inv}_J H^1(K,N)$
be the set of
![]() $J$
-invariant elements in
$J$
-invariant elements in
![]() $H^1(K,N)$
. For any
$H^1(K,N)$
. For any
![]() $\varphi \in Z^1(J,N)$
, we have
$\varphi \in Z^1(J,N)$
, we have
![]() $\varphi ^j(x) = n^{-1} \varphi (x) n^{x^{-1}}$
where
$\varphi ^j(x) = n^{-1} \varphi (x) n^{x^{-1}}$
where
![]() $n= \varphi (\,j^{-1})$
so that
$n= \varphi (\,j^{-1})$
so that
![]() $\varphi ^j \sim \varphi$
. Consequently,
$\varphi ^j \sim \varphi$
. Consequently,
![]() $\textrm {res}^J_K H^1(J,N) \subseteq \textrm {inv}_J H^1(K, N)$
.
$\textrm {res}^J_K H^1(J,N) \subseteq \textrm {inv}_J H^1(K, N)$
.
For nilpotent
![]() $J$
and
$J$
and
![]() $\varphi \in Z^1(J_p,N)$
, any
$\varphi \in Z^1(J_p,N)$
, any
![]() $j\in J$
may be written
$j\in J$
may be written
![]() $j=j_p\times j_p^{\prime}$
for
$j=j_p\times j_p^{\prime}$
for
![]() $j_p \in J_p$
and
$j_p \in J_p$
and
![]() $j_p^{\prime} \in J_p^{\prime}$
so that
$j_p^{\prime} \in J_p^{\prime}$
so that
![]() $\varphi ^j(x) = \varphi (x^{j_p^{-1}})^{j_pj_p^{\prime}} = \varphi ^{\prime}(x)^{j_p^{\prime}}$
for some
$\varphi ^j(x) = \varphi (x^{j_p^{-1}})^{j_pj_p^{\prime}} = \varphi ^{\prime}(x)^{j_p^{\prime}}$
for some
![]() $\varphi ^{\prime}\sim \varphi$
. It follows that
$\varphi ^{\prime}\sim \varphi$
. It follows that
![]() $\textrm {inv}_J H^1(J_p, N) = H^1(J_p, N)^{J_p^{\prime}}$
, that is, the
$\textrm {inv}_J H^1(J_p, N) = H^1(J_p, N)^{J_p^{\prime}}$
, that is, the
![]() $J$
-invariant elements of
$J$
-invariant elements of
![]() $H^1(J_p, N)$
are those fixed under conjugation by
$H^1(J_p, N)$
are those fixed under conjugation by
![]() $J_p^{\prime}$
.
$J_p^{\prime}$
.
To each complement
![]() $K$
of
$K$
of
![]() $N$
in
$N$
in
![]() $NJ$
, we associate
$NJ$
, we associate
![]() $\varphi _K\in Z^1(J,N)$
as follows. For
$\varphi _K\in Z^1(J,N)$
as follows. For
![]() $j\in J$
, we have
$j\in J$
, we have
![]() $j=n_j^{-1}k_j$
for unique
$j=n_j^{-1}k_j$
for unique
![]() $n_j\in N$
and
$n_j\in N$
and
![]() $k_j\in K$
; we then let
$k_j\in K$
; we then let
![]() $\varphi _K(\,j) = n_j = k_j j^{-1}$
. Conversely, for any
$\varphi _K(\,j) = n_j = k_j j^{-1}$
. Conversely, for any
![]() $\varphi \in Z^1(J,N)$
, the subgroup
$\varphi \in Z^1(J,N)$
, the subgroup
![]() $F(\varphi ) = \{\varphi (\,j)j\}_{j\in J}$
complements
$F(\varphi ) = \{\varphi (\,j)j\}_{j\in J}$
complements
![]() $N$
in
$N$
in
![]() $NJ$
. In particular,
$NJ$
. In particular,
![]() $F(\varphi _K) = K$
. Furthermore,
$F(\varphi _K) = K$
. Furthermore,
![]() $F(\varphi )$
and
$F(\varphi )$
and
![]() $F(\varphi ^{\prime})$
are
$F(\varphi ^{\prime})$
are
![]() $N$
-conjugate in
$N$
-conjugate in
![]() $NJ$
if and only if
$NJ$
if and only if
![]() $\varphi \sim \varphi ^{\prime}$
so that
$\varphi \sim \varphi ^{\prime}$
so that
![]() $F$
induces a correspondence between
$F$
induces a correspondence between
![]() $H^1(J,N)$
and the
$H^1(J,N)$
and the
![]() $N$
-conjugacy classes of complements to
$N$
-conjugacy classes of complements to
![]() $N$
in
$N$
in
![]() $NJ$
. See Serre [Reference Serre6, Ch. I §5] for further details on nonabelian group cohomology.
$NJ$
. See Serre [Reference Serre6, Ch. I §5] for further details on nonabelian group cohomology.
2. Proofs of results
We begin by establishing Lemma1.
Proof of Lemma 1. As
![]() $N$
is nilpotent, the natural projection maps
$N$
is nilpotent, the natural projection maps
![]() $N \to N_p$
induce an isomorphism:
$N \to N_p$
induce an isomorphism:
where terms
![]() $p\notin \mathcal {D}$
drop by the Schur–Zassenhaus theorem [Reference Doerk and Hawkes3, Thm. A.11.3]. Thus, we may focus our attention on
$p\notin \mathcal {D}$
drop by the Schur–Zassenhaus theorem [Reference Doerk and Hawkes3, Thm. A.11.3]. Thus, we may focus our attention on
![]() $H^1(J, N_q)$
for some prime
$H^1(J, N_q)$
for some prime
![]() $q$
. If
$q$
. If
![]() $J$
is also a
$J$
is also a
![]() $q$
-group, we are done. Otherwise, we may consider the inflation-restriction exact sequence [Reference Serre6, Sec. I.5.8]:
$q$
-group, we are done. Otherwise, we may consider the inflation-restriction exact sequence [Reference Serre6, Sec. I.5.8]:
As
![]() $H^1(J_q^{\prime}, N_q^{\,J_q})$
is trivial,
$H^1(J_q^{\prime}, N_q^{\,J_q})$
is trivial,
![]() $\textrm {res}^J_{J_q}$
is injective. For any
$\textrm {res}^J_{J_q}$
is injective. For any
![]() $\varphi \in H^1(J_q,N_q)^{J_q^{\prime}}$
, we may define
$\varphi \in H^1(J_q,N_q)^{J_q^{\prime}}$
, we may define
![]() $\tilde \varphi$
in terms of a representative crossed homomorphism as
$\tilde \varphi$
in terms of a representative crossed homomorphism as
![]() $\tilde \varphi (\,j^{\prime}j) = \varphi (\,j)$
for
$\tilde \varphi (\,j^{\prime}j) = \varphi (\,j)$
for
![]() $j\in J_q$
and
$j\in J_q$
and
![]() $j^{\prime}\in J_q^{\prime}$
. It is straightforward to verify that
$j^{\prime}\in J_q^{\prime}$
. It is straightforward to verify that
![]() $\tilde \varphi \in Z^1(J, N_q)$
and
$\tilde \varphi \in Z^1(J, N_q)$
and
![]() $\tilde \varphi |_{J_q} \sim \varphi$
. Thus,
$\tilde \varphi |_{J_q} \sim \varphi$
. Thus,
![]() $\textrm {res}^J_{J_q}$
is also surjective and thus an isomorphism. Let
$\textrm {res}^J_{J_q}$
is also surjective and thus an isomorphism. Let
![]() $v\,:\, H^1(J_q, N_q) \to H^1(J_q, N)$
denote the map induced by inclusion. From the decomposition (1),
$v\,:\, H^1(J_q, N_q) \to H^1(J_q, N)$
denote the map induced by inclusion. From the decomposition (1),
![]() $H^1(J_q, N_q) \cong H^1(J_q, N)$
, and as
$H^1(J_q, N_q) \cong H^1(J_q, N)$
, and as
is exact [Reference Serre6, Prop. I.38] where
![]() $H^1(J_q, N_q^{\prime})$
is trivial, it follows that
$H^1(J_q, N_q^{\prime})$
is trivial, it follows that
![]() $v$
is surjective and hence an isomorphism. As
$v$
is surjective and hence an isomorphism. As
![]() $\varphi \in H^1(J_p, N_p)^{J_p^{\prime}}$
if and only if
$\varphi \in H^1(J_p, N_p)^{J_p^{\prime}}$
if and only if
![]() $v(\varphi )\in H^1(J_p, N)^{J_p^{\prime}}$
, it follows that
$v(\varphi )\in H^1(J_p, N)^{J_p^{\prime}}$
, it follows that
![]() $\Phi \,:\, H^1(J,N) \to \times _{p\in \mathcal {D}} H^1(J_p, N)^{J_p^{\prime}}$
given by the composition
$\Phi \,:\, H^1(J,N) \to \times _{p\in \mathcal {D}} H^1(J_p, N)^{J_p^{\prime}}$
given by the composition
![]() $\varphi \mapsto \times _{p\in \mathcal {D}} \varphi |_{J_p}$
induces the desired isomorphism:
$\varphi \mapsto \times _{p\in \mathcal {D}} \varphi |_{J_p}$
induces the desired isomorphism:
We now show how Propositions2 and 3 follow from Lemma1.
Proof of Proposition 2. Suppose
![]() $J$
and
$J$
and
![]() $J^{\prime}$
each complement
$J^{\prime}$
each complement
![]() $N\vartriangleleft G$
as described in the hypotheses of the proposition. Let
$N\vartriangleleft G$
as described in the hypotheses of the proposition. Let
![]() $\varphi$
be a crossed homomorphism representing
$\varphi$
be a crossed homomorphism representing
![]() $J^{\prime}$
in
$J^{\prime}$
in
![]() $H^1(J,N)$
. By hypothesis,
$H^1(J,N)$
. By hypothesis,
![]() $\varphi |_{J_p}\sim 1|_{J_p}$
for every prime
$\varphi |_{J_p}\sim 1|_{J_p}$
for every prime
![]() $p$
, where
$p$
, where
![]() $1 \in Z^1(J,N)$
represents the distinguished point. Lemma1 implies
$1 \in Z^1(J,N)$
represents the distinguished point. Lemma1 implies
![]() $\varphi \sim 1$
so that
$\varphi \sim 1$
so that
![]() $J$
and
$J$
and
![]() $J^{\prime}$
are conjugate.
$J^{\prime}$
are conjugate.
Proof of Proposition 3. Suppose
![]() $G \cong N \rtimes J$
satisfies the hypotheses of the proposition. Fix a prime
$G \cong N \rtimes J$
satisfies the hypotheses of the proposition. Fix a prime
![]() $p$
. Without loss, we may suppose any two complements of
$p$
. Without loss, we may suppose any two complements of
![]() $N_p$
in
$N_p$
in
![]() $S=J_pN_p$
are conjugate in
$S=J_pN_p$
are conjugate in
![]() $G$
. If
$G$
. If
![]() $J_p^{\prime}$
is such a complement, then
$J_p^{\prime}$
is such a complement, then
![]() $J_p^{\prime} = (J_p)^g$
for some
$J_p^{\prime} = (J_p)^g$
for some
![]() $g\in G$
so that
$g\in G$
so that
![]() $J_p^{\prime} = (J_p)^{jn} = (J_p)^n$
for some
$J_p^{\prime} = (J_p)^{jn} = (J_p)^n$
for some
![]() $j\in J$
and
$j\in J$
and
![]() $n\in N$
. In particular,
$n\in N$
. In particular,
![]() $J_p^{\prime}$
is conjugate to
$J_p^{\prime}$
is conjugate to
![]() $J_p$
in
$J_p$
in
![]() $J_pN$
. Thus,
$J_pN$
. Thus,
![]() $H^1(J_p,N)$
is trivial. As the choice of prime
$H^1(J_p,N)$
is trivial. As the choice of prime
![]() $p$
was arbitrary, Lemma1 implies that
$p$
was arbitrary, Lemma1 implies that
![]() $H^1(J,N)$
is also trivial, allowing us to conclude.
$H^1(J,N)$
is also trivial, allowing us to conclude.
To prove Theorem4, we also require:
Proposition 5.
Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G\cong N \rtimes J$
where
$G\cong N \rtimes J$
where
![]() $N$
and
$N$
and
![]() $J$
are nilpotent. If for each prime
$J$
are nilpotent. If for each prime
![]() $p$
,
$p$
,
![]() $H$
contains a conjugate of some
$H$
contains a conjugate of some
![]() $J_p \in \textrm {Syl}_p(J)$
, then
$J_p \in \textrm {Syl}_p(J)$
, then
![]() $H$
contains a conjugate of
$H$
contains a conjugate of
![]() $J$
.
$J$
.
Proof of Proposition 5. It follows from the hypotheses that
![]() $H$
supplements
$H$
supplements
![]() $N$
in
$N$
in
![]() $G$
. We induct on the order of
$G$
. We induct on the order of
![]() $G$
. If
$G$
. If
![]() $H$
is a
$H$
is a
![]() $p$
-group or all of
$p$
-group or all of
![]() $G$
, the result is immediate. If multiple primes divide
$G$
, the result is immediate. If multiple primes divide
![]() $\lvert N\rvert$
, we have the nontrivial decomposition
$\lvert N\rvert$
, we have the nontrivial decomposition
![]() $N\cong N_p \times N_p^{\prime}$
for some prime
$N\cong N_p \times N_p^{\prime}$
for some prime
![]() $p$
. Induction in
$p$
. Induction in
![]() $G/N_p$
implies
$G/N_p$
implies
![]() $J^{n_0} \leq H N_p$
for some
$J^{n_0} \leq H N_p$
for some
![]() $n_0\in N_p^{\prime}$
. Induction in
$n_0\in N_p^{\prime}$
. Induction in
![]() $G/N_p^{\prime}$
implies
$G/N_p^{\prime}$
implies
![]() $J^{n_1} \leq H N_p^{\prime}$
for some
$J^{n_1} \leq H N_p^{\prime}$
for some
![]() $n_1\in N_p$
. Thus,
$n_1\in N_p$
. Thus,
![]() $J^{n_0n_1} \leq H N_p \cap HN_p^{\prime} = H$
, where the last equality proceeds from the following argument of Losey and Stonehewer [Reference Losey and Stonehewer5]. Suppose
$J^{n_0n_1} \leq H N_p \cap HN_p^{\prime} = H$
, where the last equality proceeds from the following argument of Losey and Stonehewer [Reference Losey and Stonehewer5]. Suppose
![]() $g\in H N_p \cap HN_p^{\prime}$
so that
$g\in H N_p \cap HN_p^{\prime}$
so that
![]() $g=h_0n_0 = h_1n_1$
for some
$g=h_0n_0 = h_1n_1$
for some
![]() $h_0, h_1\in H$
,
$h_0, h_1\in H$
,
![]() $n_0\in N_p$
and
$n_0\in N_p$
and
![]() $n_1\in N_p^{\prime}$
. Then
$n_1\in N_p^{\prime}$
. Then
![]() $(h_1)^{-1} h_0 = n_1(n_0)^{-1} \in H$
. As
$(h_1)^{-1} h_0 = n_1(n_0)^{-1} \in H$
. As
![]() $n_0$
and
$n_0$
and
![]() $n_1$
commute and have coprime orders, it follows that
$n_1$
commute and have coprime orders, it follows that
![]() $n_0, n_1 \in H$
so
$n_0, n_1 \in H$
so
![]() $g\in H$
.
$g\in H$
.
We now proceed under the assumption that
![]() $N=N_q$
for some prime
$N=N_q$
for some prime
![]() $q$
. Upon switching to a conjugate of
$q$
. Upon switching to a conjugate of
![]() $H$
if necessary, we may suppose that
$H$
if necessary, we may suppose that
![]() $J_q \leq H$
. Let
$J_q \leq H$
. Let
![]() $Z$
denote the center of
$Z$
denote the center of
![]() $N$
. If
$N$
. If
![]() $Z \cap H$
were nontrivial, then induction in
$Z \cap H$
were nontrivial, then induction in
![]() $G/(Z\cap H)$
would allow us to conclude. Otherwise, in
$G/(Z\cap H)$
would allow us to conclude. Otherwise, in
![]() $G/Z$
, induction implies that
$G/Z$
, induction implies that
![]() $J^gZ/Z \leq ZH/Z$
for some
$J^gZ/Z \leq ZH/Z$
for some
![]() $g\in G$
. Let
$g\in G$
. Let
![]() $\psi \,:\, H \to HZ/Z$
denote the isomorphism between
$\psi \,:\, H \to HZ/Z$
denote the isomorphism between
![]() $H$
and
$H$
and
![]() $HZ/Z$
. Then
$HZ/Z$
. Then
![]() $K = \psi ^{-1}(J^gZ/Z)$
complements
$K = \psi ^{-1}(J^gZ/Z)$
complements
![]() $N\cap H$
in
$N\cap H$
in
![]() $H$
and
$H$
and
![]() $N$
in
$N$
in
![]() $G$
. Let
$G$
. Let
![]() $\varphi \in Z^1(K,N)$
correspond to
$\varphi \in Z^1(K,N)$
correspond to
![]() $J$
. Then
$J$
. Then
![]() $\varphi |_{K_q}$
corresponds to
$\varphi |_{K_q}$
corresponds to
![]() $J_q$
where
$J_q$
where
![]() $[\varphi |_{K_q}]\in H^1(K_q, H \cap N)^{K_q^{\prime}}\cong H^1(K, H \cap N)$
. In particular, there exists a complement, say
$[\varphi |_{K_q}]\in H^1(K_q, H \cap N)^{K_q^{\prime}}\cong H^1(K, H \cap N)$
. In particular, there exists a complement, say
![]() $L$
, to
$L$
, to
![]() $H\cap N$
in
$H\cap N$
in
![]() $H$
that contains
$H$
that contains
![]() $J_q$
.
$J_q$
.
![]() $L$
will also complement
$L$
will also complement
![]() $N$
in
$N$
in
![]() $G$
, and as
$G$
, and as
![]() $\textrm {Syl}_p(L) \subseteq \textrm {Syl}_p(G)$
for all primes
$\textrm {Syl}_p(L) \subseteq \textrm {Syl}_p(G)$
for all primes
![]() $p\ne q$
, we may apply Proposition2 to conclude that
$p\ne q$
, we may apply Proposition2 to conclude that
![]() $J^{g^{\prime}} = L \leq H$
for some
$J^{g^{\prime}} = L \leq H$
for some
![]() $g^{\prime} \in G$
.
$g^{\prime} \in G$
.
With this, we are prepared to prove Theorem4.
Proof of Theorem 4. Given
![]() $J$
,
$J$
,
![]() $N$
, and
$N$
, and
![]() $\Omega$
as described in the hypotheses of the theorem, let
$\Omega$
as described in the hypotheses of the theorem, let
![]() $G= N \rtimes J$
denote the induced semidirect product and consider the stabilizer subgroup
$G= N \rtimes J$
denote the induced semidirect product and consider the stabilizer subgroup
![]() $G_\alpha$
for some
$G_\alpha$
for some
![]() $\alpha \in \Omega$
. As
$\alpha \in \Omega$
. As
![]() $N$
acts transitively,
$N$
acts transitively,
![]() $G=NG_\alpha$
. For each prime
$G=NG_\alpha$
. For each prime
![]() $p$
, the hypotheses of the theorem imply
$p$
, the hypotheses of the theorem imply
![]() $(J_p)^{n_p} \leq G_\alpha$
for some
$(J_p)^{n_p} \leq G_\alpha$
for some
![]() $J_p \in \textrm {Syl}_p(J)$
and
$J_p \in \textrm {Syl}_p(J)$
and
![]() $n_p\in N$
so that Proposition5 allows us to conclude
$n_p\in N$
so that Proposition5 allows us to conclude
![]() $J^g \leq G_\alpha$
for some
$J^g \leq G_\alpha$
for some
![]() $g\in G$
. It follows that
$g\in G$
. It follows that
![]() $J$
fixes
$J$
fixes
![]() $g\cdot \alpha$
.
$g\cdot \alpha$
.
3. Conclusion
We conclude with a brief discussion of analogous results in the abelian case. For arbitrary
![]() $J$
acting on abelian
$J$
acting on abelian
![]() $N$
, the restriction map
$N$
, the restriction map
![]() $\textrm {res}^J_{J_p}\,:\, H^1(J,N)_{(p)} \xrightarrow {\cong } \textrm {inv}_J H^1(J_p, N)$
induces an isomorphism for each prime
$\textrm {res}^J_{J_p}\,:\, H^1(J,N)_{(p)} \xrightarrow {\cong } \textrm {inv}_J H^1(J_p, N)$
induces an isomorphism for each prime
![]() $p$
, where
$p$
, where
![]() $H^1(J,N)_{(p)}$
is the
$H^1(J,N)_{(p)}$
is the
![]() $p$
-primary component of
$p$
-primary component of
![]() $H^1(J,N)$
and
$H^1(J,N)$
and
![]() $J_p\in \textrm {Syl}_p(J)$
. Consequently, it follows from the primary decomposition of
$J_p\in \textrm {Syl}_p(J)$
. Consequently, it follows from the primary decomposition of
![]() $H^1(J,N)$
that [Reference Brown1, Thm. III.10.3]:
$H^1(J,N)$
that [Reference Brown1, Thm. III.10.3]:
Furthermore, for abelian
![]() $N$
, suppose
$N$
, suppose
![]() $G = N \rtimes J$
acts on some non-empty set
$G = N \rtimes J$
acts on some non-empty set
![]() $\Omega$
, where the action of
$\Omega$
, where the action of
![]() $N$
is transitive, and for each prime
$N$
is transitive, and for each prime
![]() $p$
a Sylow
$p$
a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $J$
fixes an element of
$J$
fixes an element of
![]() $\Omega$
. Then, for arbitrary
$\Omega$
. Then, for arbitrary
![]() $\alpha \in \Omega$
, the stabilizer
$\alpha \in \Omega$
, the stabilizer
![]() $G_\alpha$
splits over
$G_\alpha$
splits over
![]() $G_\alpha \cap N$
by Gaschütz’s theorem [Reference Doerk and Hawkes3, Thm. A.11.2] and is locally conjugate and thus conjugate to
$G_\alpha \cap N$
by Gaschütz’s theorem [Reference Doerk and Hawkes3, Thm. A.11.2] and is locally conjugate and thus conjugate to
![]() $J$
by an argument analogous to the proof of Proposition5. In particular,
$J$
by an argument analogous to the proof of Proposition5. In particular,
![]() $J$
fixes an element of
$J$
fixes an element of
![]() $\Omega$
. In this note, we find that the decomposition (3) and fixed point result continue to hold for nilpotent
$\Omega$
. In this note, we find that the decomposition (3) and fixed point result continue to hold for nilpotent
![]() $N$
if
$N$
if
![]() $J$
is also nilpotent.
$J$
is also nilpotent.
Acknowledgments
The author thanks the editor C. M. Roney-Dougal and an anonymous reviewer for detailed feedback which considerably improved the manuscript.
Competing interests
The author declares none.