Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-21T15:40:37.790Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hilbert scheme of the moduli space of torsion-free sheaves on surfaces

Part of: Surfaces and higher-dimensional varieties Families, fibrations

Published online by Cambridge University Press:  02 February 2023

O. Mata-Gutiérrez ,
L. Roa-Leguizamón Open the ORCID record for L. Roa-Leguizamón [Opens in a new window]  and
H. Torres-López
O. Mata-Gutiérrez
Affiliation:
Departamento De Matemáticas, Centro Universitario De Ciencias Exactas E Ingenierías, Universidad De Guadalajara, Avenida Revolución 1500, Guadalajara, Jalisco, México
L. Roa-Leguizamón*
Affiliation:
Departamento De Matemáticas, Universidad De Los Andes, Carrera 1 #18A-12, 111 711, Bogota, Colombia
H. Torres-López
Affiliation:
Conacyt - U. A. Matemáticas, U. Autónoma De Zacatecas, Calzada Solidaridad Entronque Paseo A La Bufa, C.P. 98000 Zacatecas, Zac., México
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to determine a bound of the dimension of an irreducible component of the Hilbert scheme of the moduli space of torsion-free sheaves on surfaces. Let X be a nonsingular irreducible complex surface, and let E be a vector bundle of rank n on X. We use the m-elementary transformation of E at a point 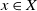$x \in X$ to show that there exists an embedding from the Grassmannian variety 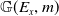$\mathbb{G}(E_x,m)$ into the moduli space of torsion-free sheaves 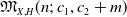$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$ which induces an injective morphism from 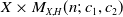$X \times M_{X,H}(n;\,c_1,c_2)$ to 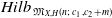$Hilb_{\, \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$.

Keywords

elementary transformationmoduli of vector bundlesmoduli of sheavesHilbert scheme

MSC classification

Primary: 14D20: Algebraic moduli problems, moduli of vector bundles
Secondary: 14J60: Vector bundles on surfaces and higher-dimensional varieties, and their moduli
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 2 , May 2023 , pp. 414 - 429
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A., Compact complex surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, 2nd edition (Springer-Verlag, Berlin, 2004), xii+436.CrossRefGoogle Scholar
Brambila-Paz, L. and Mata-Gutiérrez, O., On the Hilbert Scheme of the moduli space of vector bundles over an algebraic curve, Manuscripta Math. 142 (2013), 525–544.CrossRefGoogle Scholar
Coskun, I. and Huizenga, J., The ample cone of moduli spaces of sheaves on surfaces and the Brill-Noether Problem, Manuscripta Math. 142 (2013), 525–544.Google Scholar
Coskun, I. and Huizenga, J., Brill-Noether theorems and globally generated vector bundles on Hirzebruch surfaces, Nagoya Math. J. 238 (2020), 1–36.CrossRefGoogle Scholar
Coskun, I. and Huizenga, J., The birational geometry of the moduli spaces of sheaves on $\mathbb{P}^2$ , in Proceedings of the Gökova Geometry-Topology Conference 2014, Gökova Geometry/Topology Conference (GGT), Gökova (2015), 114–155.Google Scholar
Coskun, I. and Huizenga, J., The moduli spaces of sheaves on surfaces, pathologies and Brill-Noether problems, in Geometry of moduli, Abel Symposia, vol. 14 (Springer, Cham, 2018), 75–105.CrossRefGoogle Scholar
L. Costa and R. M. Miró-roig, Elementary transformations and the rationality of the Moduli Spaces of Vector Bundles on $\mathbb{P}^2$ , Manuscripta Math. 113(1) (2004), 69–84.CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., 3264 and all that a second course on algebraic geometry (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Fantechi, B., et al., Fundamental algebraic geometry: Grothendieck’s FGA explained , Mathematical Surveys and Monographs, vol. 123 (2005).Google Scholar
Friedman, R., Algebraic surfaces and holomorphic vector bundles. Universitext (Springer-Verlag, New York, 1998), x+328.CrossRefGoogle Scholar
Gottsche, L., Change of polarization and Hodge numbers of moduli spaces of torsion free sheaves on surfaces, Mathematische Zeitschrift 223 (1996), 247–260.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry . Graduate Texts in Mathematics, vol. 52 (Springer-Verlag, New York-Heidelberg, 1977), xvi+496.Google Scholar
Hirshowitz, A. and Hulek, K., Complete families of stable vector bundles over $\mathbb{P}_2$ , in Complex Analysis and Algebraic Geometry. Lecture Notes in Mathematics (Springer Verlag, 1985).CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, Aspects of Mathematics, vol. E31 (Friedr. Vieweg Sohn, Braunschweig, 1997), xiv+269.10.1007/978-3-663-11624-0CrossRefGoogle Scholar
Le Potier, J., Lectures on vector bundles. Translated by Maciocia, A.. Cambridge Studies in Advanced Mathematics, vol. 54 (Cambridge University Press, Cambridge, 1997), viii+251.Google Scholar
Maruyama, M., Elementary transformations in the theory of algebraic vector bundles , Lecture Notes in Mathematics, vol. 961 (2006), 241–266.Google Scholar
Maruyama, M., On a family of algebraic vector bundles, in Number theory, algebraic geometry and commutative algebra, in honor of Y. Akizuki (Kinokuniya, Tokyo, 1973), 95–146.Google Scholar
Maruyama, M., Openness of a family of torsion free sheaves, J. Math Kyoto Univ. 16(3) (1976), 627–637.Google Scholar
Mumford, D., Lectures on curves on an algebraic surface. With a section by G. M. Bergman. Annals of Mathematics Studies, vol. 59 (Princeton University Press, Princeton, N.J., 1966), xi+200.Google Scholar
Narasimhan, M. S. and Ramanan, S., Geometry of Hecke Cycles I. C. P. Ramanujam-a tribute, Tata Institute of Fundamental Research, vol. 8 (Springer, Berlin-New York, 1978), 291–345.Google Scholar
Narasimhan, M. S. and Ramanan, S., Deformations of the moduli space of vector bundles over an algebraic curve, Ann. Math. 101(3) (1975), 391–417. https://doi.org/10.2307/1970933.CrossRefGoogle Scholar
Newstead, P. E., Introduction to moduli problems and orbit spaces, Tata Institute of Fundamental Research Lectures on Mathematics and Physics, vol. 51 (Tata Institute of Fundamental Research, Bombay; by the Narosa Publishing House, New Delhi, 1978), vi+183.Google Scholar
Okonek, C., Schneider, M. and Spindler, H., Vector bundles on complex projective spaces , Progress in Mathematics, vol. 3 (Birkhäuser, Boston, MA, 1980), vii+389.Google Scholar
Stromme, S. A., Ample divisors on fine moduli spaces on the projective plane, Math. Z. 187(3) (1984), 405–423.CrossRefGoogle Scholar
Tyurin, A., Vector bundles, in Collected works, volume I (Bogomolov F., Gorodentsev A., Pidstrigach V., Reid M. and Tyurin N., Editors) (Universitätsverlag Göttingen, 2008), vii+389.CrossRefGoogle Scholar