No CrossRef data available.
Published online by Cambridge University Press: 07 April 2020
Consider the following two eigenvalue problems: (0.1)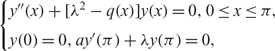 \begin{cases}\label{eqn:1abs}y"(x)+[\lambda^2-q(x)]y(x)=0, 0 \leq x \leq \pi,\\[3pt] y(0)=0, ay'(\pi)+\lambda y(\pi)=0, \end{cases}
\begin{cases}\label{eqn:1abs}y"(x)+[\lambda^2-q(x)]y(x)=0, 0 \leq x \leq \pi,\\[3pt] y(0)=0, ay'(\pi)+\lambda y(\pi)=0, \end{cases}
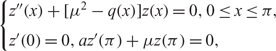 \begin{cases} z"(x)+[\mu^2-q(x)]z(x)=0, 0 \leq x \leq \pi,\\[3pt] z'(0)=0, az'(\pi)+\mu z(\pi)=0, \end{cases}
\begin{cases} z"(x)+[\mu^2-q(x)]z(x)=0, 0 \leq x \leq \pi,\\[3pt] z'(0)=0, az'(\pi)+\mu z(\pi)=0, \end{cases}
where 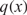 $q(x)$
is real-valued and integrable on [0,
$q(x)$
is real-valued and integrable on [0, 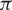 $\pi$
]. Let
$\pi$
]. Let  $\{\lambda_n\}_{n\in \mathbb{Z}\setminus \{0\}}$
and
$\{\lambda_n\}_{n\in \mathbb{Z}\setminus \{0\}}$
and  $\{\mu_n\}_{n\in \mathbb{Z}\setminus \{0\}}$
denote the eigenvalues of equations (0.1) and (0.2), respectively. Then
$\{\mu_n\}_{n\in \mathbb{Z}\setminus \{0\}}$
denote the eigenvalues of equations (0.1) and (0.2), respectively. Then
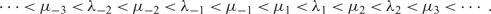 \[\cdots\lt\mu_{-3}\lt\lambda_{-2}\lt\mu_{-2}\lt\lambda_{-1}\lt\mu_{-1}\lt\mu_1\lt\lambda_1\lt\mu_2\lt\lambda_2\lt\mu_3\lt\cdots.\]
\[\cdots\lt\mu_{-3}\lt\lambda_{-2}\lt\mu_{-2}\lt\lambda_{-1}\lt\mu_{-1}\lt\mu_1\lt\lambda_1\lt\mu_2\lt\lambda_2\lt\mu_3\lt\cdots.\]
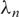 $\lambda_n$
(
$\lambda_n$
(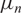 $\mu_n$
, respectively) in (0,
$\mu_n$
, respectively) in (0, 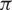 $\pi$
) is equal to
$\pi$
) is equal to 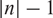 $|n|-1$
.
$|n|-1$
.