Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T17:29:20.843Z Has data issue: false hasContentIssue false
  • English
  • Français

A structure theorem for stochastic processes indexed by the discrete hypercube

Part of: Stochastic processes Extremal combinatorics

Published online by Cambridge University Press:  28 January 2021

Pandelis Dodos  and
Konstantinos Tyros
Pandelis Dodos
Affiliation:
Department of Mathematics, University of Athens, Panepistimiopolis 157 84, Athens, Greece; E-mail: [email protected]
Konstantinos Tyros
Affiliation:
Department of Mathematics, University of Athens, Panepistimiopolis 157 84, Athens, Greece; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a finite set with 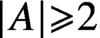, let n be a positive integer, and let 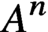$A^n$ denote the discrete 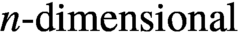$n\text {-dimensional}$ hypercube (that is, 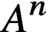$A^n$ is the Cartesian product of n many copies of A). Given a family 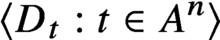$\langle D_t:t\in A^n\rangle $ of measurable events in a probability space (a stochastic process), what structural information can be obtained assuming that the events 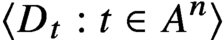$\langle D_t:t\in A^n\rangle $ are not behaving as if they were independent? We obtain an answer to this problem (in a strong quantitative sense) subject to a mild ‘stationarity’ condition. Our result has a number of combinatorial consequences, including a new (and the most informative so far) proof of the density Hales-Jewett theorem.

MSC classification

Primary: 05D10: Ramsey theory 05D40: Probabilistic methods
Secondary: 60G99: None of the above, but in this section
Type
Foundations
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Austin, T., ‘Deducing the density Hales–Jewett theorem from an infinitary removal lemma’, J. Theor. Probab. 24 (2011), 615–633.CrossRefGoogle Scholar
Dodos, P. and Kanellopoulos, V., Ramsey Theory for Product Spaces, Mathematical Surveys and Monographs, 212 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Dodos, P., Kanellopoulos, V. and Tyros, K., ‘A simple proof of the density Hales-Jewett theorem’, Int. Math. Res. Not. 12 (2014), 3340–3352.CrossRefGoogle Scholar
Dodos, P., Kanellopoulos, V. and Tyros, K., ‘Measurable events indexed by words’, J. Comb. Theory, Ser. A 127 (2014), 176–223.Google Scholar
Dodos, P., Kanellopoulos, V. and Tyros, K., ‘A concentration inequality for product spaces’, J. Funct. Anal. 270 (2016), 609–620.CrossRefGoogle Scholar
Durrett, R., Probability: Theory and Examples, Cambridge Series in Statistical and Probabilistic Mathematics, fourth edition (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y., ‘Idempotents in compact semigroups and Ramsey theory’, Israel J. Math. 68 (1989), 257–270.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y., ‘A density version of the Hales-Jewett theorem’, J. Anal. Math. 57 (1991), 64–119.CrossRefGoogle Scholar
Graham, R. L. and Rothschild, B. L., ‘Ramsey’s theorem for $n$-parameter sets’, Trans. Amer. Math. Soc. 159 (1971), 257–292.Google Scholar
Graham, R. L., Rothschild, B. L. and Spencer, J. H., Ramsey Theory, second edition (John Wiley & Sons, Hoboken, NJ, 1980).Google Scholar
Hales, A. H. and Jewett, R. I., ‘Regularity and positional games’, Trans. Amer. Math. Soc. 106 (1963), 222–229.CrossRefGoogle Scholar
Polymath, D. H. J., ‘Density Hales-Jewett and Moser numbers’, in An Irregular Mind. Szemerédi Is 70, Bolyai Society Mathematical Studies, 21 (Springer, Berlin, 2010), 689–753.CrossRefGoogle Scholar
Polymath, D. H. J., ‘A new proof of the density Hales-Jewett theorem’, Ann. Math. 175 (2012), 1283–1327.Google Scholar
Roth, K. F., ‘On certain sets of integers’, J. London Math. Soc. 28 (1953), 104–109.CrossRefGoogle Scholar
Shelah, S., ‘Primitive recursive bounds for van der Waerden numbers’, J. Amer. Math. Soc. 1 (1988), 683–697.CrossRefGoogle Scholar
Sperner, E., ‘Ein Satz über Untermengen einer endlichen Menge’, Math. Z. 27 (1928) 544–548.CrossRefGoogle Scholar
Tao, T., An Epsilon of Room, II: Pages from Year Three of a Mathematical Blog (American Mathematical Society, Providence, RI, 2011).CrossRefGoogle Scholar
Tao, T. and Vu, V., Additive Combinatorics, Cambridge Studies in Advanced Mathematics, 105 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Tyros, K., ‘On colorings of variable words’, Discr. Math. 338 (2015), 1025–1028.CrossRefGoogle Scholar