Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T07:33:17.692Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FREE ENERGY OF THE TWO-DIMENSIONAL DILUTE BOSE GAS. I. LOWER BOUND

Part of: Rings and algebras with additional structure Modules, bimodules and ideals

Published online by Cambridge University Press:  21 April 2020

ANDREAS DEUCHERT Open the ORCID record for ANDREAS DEUCHERT [Opens in a new window] ,
SIMON MAYER  and
ROBERT SEIRINGER Open the ORCID record for ROBERT SEIRINGER [Opens in a new window]
ANDREAS DEUCHERT
Affiliation:
Institute of Mathematics, University of Zurich, Winterthurerstrasse 190, 8057Zurich, Switzerland; [email protected] Institute of Science and Technology Austria (IST Austria), Am Campus 1, 3400Klosterneuburg, Austria; [email protected], [email protected]
SIMON MAYER
Affiliation:
Institute of Science and Technology Austria (IST Austria), Am Campus 1, 3400Klosterneuburg, Austria; [email protected], [email protected]
ROBERT SEIRINGER
Affiliation:
Institute of Science and Technology Austria (IST Austria), Am Campus 1, 3400Klosterneuburg, Austria; [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a lower bound for the free energy (per unit volume) of the two-dimensional Bose gas in the thermodynamic limit. We show that the free energy at density 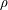$\unicode[STIX]{x1D70C}$ and inverse temperature 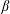$\unicode[STIX]{x1D6FD}$ differs from the one of the noninteracting system by the correction term 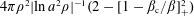$4\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70C}^{2}|\ln \,a^{2}\unicode[STIX]{x1D70C}|^{-1}(2-[1-\unicode[STIX]{x1D6FD}_{\text{c}}/\unicode[STIX]{x1D6FD}]_{+}^{2})$. Here, $a$ is the scattering length of the interaction potential, 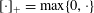$[\cdot ]_{+}=\max \{0,\cdot \}$ and 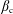$\unicode[STIX]{x1D6FD}_{\text{c}}$ is the inverse Berezinskii–Kosterlitz–Thouless critical temperature for superfluidity. The result is valid in the dilute limit 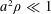$a^{2}\unicode[STIX]{x1D70C}\ll 1$ and if 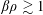$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70C}\gtrsim 1$.

MSC classification

Primary: 16W10: Rings with involution; Lie, Jordan and other nonassociative structures
Secondary: 16D50: Injective modules, self-injective rings
Type
Mathematical Physics
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e20
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Andersen, J. O., ‘Ground state pressure and energy density of an interacting homogeneous Bose gas in two dimensions’, Eur. Phys. J. B 28 (2002), 389.CrossRefGoogle Scholar
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E. and Cornell, E. A., ‘Observation of Bose–Einstein condensation in a dilute atomic vapor’, Science 269 (1995), 198–201.CrossRefGoogle Scholar
Berezin, F. A., ‘Covariant and contravariant symbols of operators’, Izv. Akad. Nauk. Ser. Mat. 36 (1972), 1134–1167. English translation: USSR Izv. 6 (1973), 1117–1151.Google Scholar
Berezin, F. A., ‘General concept of quantization’, Comm. Math. Phys. 40 (1975), 153–174.CrossRefGoogle Scholar
Berezinskii, V. L., ‘Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group I. Classical systems’, Sov. Phys. JETP 32 (1971), 493.Google Scholar
Berezinskii, V. L., ‘Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group II. Quantum systems’, Sov. Phys. JETP 34 (1972), 610.Google Scholar
Boccato, C., Brennecke, C., Cenatiempo, S. and Schlein, B., ‘Bogoliubov theory in the Gross–Pitaevskii limit’, Acta Math. 222 (2019), 219–335.CrossRefGoogle Scholar
Brietzke, B. and Solovej, J. P., ‘The second-order correction to the ground state energy of the dilute bose gas’, Ann. Henri Poincaré 21 (2020), 571–626.CrossRefGoogle Scholar
Davis, K. B., Mewes, M.-O., Andrews, M. R., van Druten, N. J., Durfee, D. S., Kurn, D. M. and Ketterle, W., ‘Bose–Einstein condensation in a gas of sodium atoms’, Phys. Rev. Lett. 75 (1995), 3969–3973.CrossRefGoogle Scholar
Dyson, F. J., ‘Ground-state energy of a hard-sphere gas’, Phys. Rev. 106 (1957), 20–26.CrossRefGoogle Scholar
Erdős, L., Schlein, B. and Yau, H.-T., ‘Ground-state energy of a low-density Bose gas: a second-order upper bound’, Phys. Rev. A 78 (2008), 053627.CrossRefGoogle Scholar
Fisher, D. S. and Hohenberg, P. C., ‘Dilute Bose gas in two dimensions’, Phys. Rev. B 37 (1988), 4936–4943.CrossRefGoogle ScholarPubMed
Fournais, S., Napiórkowski, M., Reuvers, R. and Solovej, J. P., ‘Ground state energy of a dilute two-dimensional Bose gas from the Bogoliubov free energy functional’, J. Math. Phys. 60 071903 (2019).CrossRefGoogle Scholar
Fournais, S. and Solovej, J. P., ‘The energy of dilute Bose gases’, Preprint, 2019, arXiv:1904.06164 [math-ph].Google Scholar
Giuliani, A. and Seiringer, R., ‘The ground state energy of the weakly interacting Bose gas at high density’, J. Stat. Phys. 135 (2009), 915–934.CrossRefGoogle Scholar
Hainzl, C. and Seiringer, R., ‘General decomposition of radial functions on ℝn and applications to N-body quantum systems’, Lett. Math. Phys. 61 (2002), 75–84.CrossRefGoogle Scholar
Hohenberg, P. C., ‘Existence of long-range order in one and two dimensions’, Phys. Rev. 158(2) (1967), 383–386.CrossRefGoogle Scholar
Kosterlitz, J. M., ‘The critical properties of the two-dimensional xy model’, J. Phys. C 7 (1974), 1046.CrossRefGoogle Scholar
Kosterlitz, J. M. and Thouless, D. J., ‘Ordering, metastability and phase transitions in two-dimensional systems’, J. Phys. C 6 (1973), 1181.CrossRefGoogle Scholar
Landon, B. and Seiringer, R., ‘The scattering length at positive temperature’, Lett. Math. Phys. 100 (2012), 237–243.CrossRefGoogle Scholar
Lee, T. D., Huang, K. and Yang, C. N., ‘Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties’, Phys. Rev. 106 (1957), 1135–1145.CrossRefGoogle Scholar
Lee, T. D. and Yang, C. N., ‘Many-body problem in quantum mechanics and quantum statistical mechanics’, Phys. Rev. 105 (1957), 1119–1120.CrossRefGoogle Scholar
Lieb, E. H., The Bose Fluid, (ed. Brittin, W. E.) Lecture Notes in Theoretical Physics VIIC (Univ. of Colorado Press, Boulder, Colorado, USA, 1964), 175–224.Google Scholar
Lieb, E. H., ‘The classical limit of quantum spin systems’, Comm. Math. Phys. 31 (1973), 327–340.CrossRefGoogle Scholar
Lieb, E. H., Seiringer, R. and Solovej, J. P., ‘Ground-state energy of the low-density Fermi gas’, Phys. Rev. A 71 (2005), 053605.CrossRefGoogle Scholar
Lieb, E. H., Seiringer, R. and Yngvason, J., ‘Bosons in a trap: a rigorous derivation of the Gross–Pitaevskii energy functional’, Phys. Rev. A 61 (2000), 043602.CrossRefGoogle Scholar
Lieb, E. H., Seiringer, R. and Yngvason, J., ‘Justification of c-number substitutions in bosonic Hamiltonians’, Phys. Rev. Lett. 94 (2005), 080401.CrossRefGoogle ScholarPubMed
Lieb, E. H. and Yngvason, J., ‘Ground state energy of the low density Bose gas’, Phys. Rev. Lett. 80 (1998), 2504–2507.CrossRefGoogle Scholar
Lieb, E. H. and Yngvason, J., ‘The ground state energy of a dilute two-dimensional Bose gas’, J. Stat. Phys. 103 (2001), 509–526.CrossRefGoogle Scholar
Liu, L. and Wong, K. W., ‘Bose system of hard spheres’, Phys. Rev. 132 (1963), 1349.CrossRefGoogle Scholar
Mayer, S. and Seiringer, R., ‘The free energy of the two-dimensional dilute Bose gas. II. Upper bound’, Preprint, 2020, arXiv:2002.08281 [math-ph].Google Scholar
Mermin, N. D. and Wagner, H., ‘Absence of Ferromagnetism or Antiferromagnetism in one- or two-dimensional isotropic Heisenberg models’, Phys. Rev. Lett. 17(22) (1966), 1133–1136.CrossRefGoogle Scholar
Mora, C. and Castin, Y., ‘Ground state energy of the two-dimensional weakly interacting Bose gas: first correction beyond Bogoliubov theory’, Phys. Rev. Lett. 102 (2009), 180404.CrossRefGoogle ScholarPubMed
Napiórkowski, M., Reuvers, R. and Solovej, J. P., ‘The Bogoliubov free energy functional II: the dilute limit’, Comm. Math. Phys. 360 (2017), 347–403.CrossRefGoogle Scholar
Napiórkowski, M., Reuvers, R. and Solovej, J. P., ‘Calculation of the critical temperature of a dilute Bose gas in the Bogoliubov approximation’, Europhys. Lett. 121 (2018), 10007.CrossRefGoogle Scholar
Napiórkowski, M., Reuvers, R. and Solovej, J. P., ‘The Bogoliubov free energy functional I: existence of minimizers and phase diagram’, Arch. Ration. Mech. Anal. 229 (2018), 1037–1090.CrossRefGoogle Scholar
Ohya, M. and Petz, D., Quantum Entropy and its Use, Texts and Monographs in Physics (Springer, Berlin, Heidelberg, 2004).Google Scholar
Popov, V. N., Functional Integrals in Quantum Field Theory and Statistical Physics (Reidel, Dordrecht, 1983).CrossRefGoogle Scholar
Robinson, D. W., The Thermodynamic Pressure in Quantum Statistical Mechanics (Springer, Berlin, Heidelberg, New York, 1971).CrossRefGoogle Scholar
Ruelle, D., Statistical Mechanics: Rigorous Results (W. A. Benjamin, Inc., Reading, MA, 1969).Google Scholar
Schick, M., ‘Two-dimensional system of hard core bosons’, Phys. Rev. A 3 (1971), 1067–1073.CrossRefGoogle Scholar
Seiringer, R., ‘A correlation estimate for quantum many-body systems at positive temperature’, Rev. Math. Phys. 18 (2006), 233–253.CrossRefGoogle Scholar
Seiringer, R., ‘The thermodynamic pressure of a dilute Fermi gas’, Comm. Math. Phys. 261 (2006), 729–758.CrossRefGoogle Scholar
Seiringer, R., ‘Free energy of a dilute Bose gas: lower bound’, Comm. Math. Phys. 279 (2008), 595–636.CrossRefGoogle Scholar
Simon, B., ‘The bound state of weakly coupled Schrödinger operators in one and two dimensions’, Ann. Phys. (2) 97 (1975), 279–288.CrossRefGoogle Scholar
Wu, T. T., ‘Ground state of a Bose system of hard spheres’, Phys. Rev. 115 (1959), 1390.CrossRefGoogle Scholar
Yau, H.-T. and Yin, J., ‘The second order upper bound for the ground energy of a Bose gas’, J. Stat. Phys. 136 (2009), 453–503.CrossRefGoogle Scholar
Yin, J., ‘Free energies of dilute Bose gases: upper bound’, J. Stat. Phys. 141 (2010), 683–726.CrossRefGoogle Scholar