Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-17T19:03:09.201Z Has data issue: false hasContentIssue false
  • English
  • Français

EISENSTEIN–KRONECKER SERIES VIA THE POINCARÉ BUNDLE

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  30 September 2019

JOHANNES SPRANG Open the ORCID record for JOHANNES SPRANG [Opens in a new window]
JOHANNES SPRANG*
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg, Germany; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A classical construction of Katz gives a purely algebraic construction of Eisenstein–Kronecker series using the Gauß–Manin connection on the universal elliptic curve. This approach gives a systematic way to study algebraic and 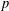$p$-adic properties of real-analytic Eisenstein series. In the first part of this paper we provide an alternative algebraic construction of Eisenstein–Kronecker series via the Poincaré bundle. Building on this, we give in the second part a new conceptional construction of Katz’ two-variable 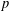$p$-adic Eisenstein measure through 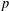$p$-adic theta functions of the Poincaré bundle.

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e34
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2019

References

Bannai, K. and Kings, G., ‘ p-adic elliptic polylogarithm, p-adic Eisenstein series and Katz measure’, Amer. J. Math. 132(6) (2010), 1609–1654.Google Scholar
Bannai, K. and Kings, G., ‘ p-adic Beilinson conjecture for ordinary Hecke motives associated to imaginary quadratic fields’, inAlgebraic Number Theory and Related Topics 2009, RIMS Kôkyûroku Bessatsu, B25 (Res. Inst. Math. Sci. (RIMS), Kyoto, 2011), 9–30.Google Scholar
Bannai, K. and Kobayashi, S., ‘Algebraic theta functions and the p-adic interpolation of Eisenstein–Kronecker numbers’, Duke Math. J. 153(2) (2010), 229–295.Google Scholar
Bannai, K., Kobayashi, S. and Tsuji, T., ‘On the de Rham and p-adic realizations of the elliptic polylogarithm for CM elliptic curves’, Ann. Sci. Éc. Norm. Supér. (4) 43(2) (2010), 185–234.Google Scholar
Edixhoven, B., van der Geer, G. and Moonen, B., ‘Abelian varieties’, Preprint, 2012, available at http://gerard.vdgeer.net/AV.pdf, p. 331.Google Scholar
Görtz, U. and Wedhorn, T., Algebraic Geometry I, Advanced Lectures in Mathematics (Vieweg + Teubner, Wiesbaden, 2010), Schemes with examples and exercises.Google Scholar
Grothendieck, A., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III’, Publ. Math. Inst. Hautes Études Sci. 28(1) (1966), 5–248.Google Scholar
Grothendieck, A., Raynaud, M. and Rim, D. S., ‘Groupes de monodromie en géométrie algébrique. I’, inSéminaire de Géométrie Algébrique du Bois-Marie 1967–1969 (SGA 7 I), Lecture Notes in Mathematics, 288 (Springer, Berlin, Heidelberg, 1972).Google Scholar
Kato, K., ‘ p-adic Hodge theory and values of zeta functions of modular forms’, Astérisque 295 (2004), ix, 117–290. Cohomologies $p$ -adiques et applications arithmétiques. III.Google Scholar
Katz, N. M., ‘ p-adic interpolation of real analytic Eisenstein series’, Ann. of Math. (2) 104(3) (1976), 459–571.Google Scholar
Katz, N. M., ‘The Eisenstein measure and p-adic interpolation’, Amer. J. Math. 99(2) (1977), 238–311.Google Scholar
Mazur, B. and Messing, W., Universal Extensions and One Dimensional Crystalline Cohomology, Lecture Notes in Mathematics, 370 (Springer, Berlin–New York, 1974).Google Scholar
Norman, P., ‘Explicit p-adic theta functions’, Invent. Math. 83(1) (1986), 41–57.Google Scholar
Oda, T., ‘The first de Rham cohomology group and Dieudonné modules’, Ann. Sci. Éc. Norm. Supér (4) 2 (1969), 63–135.Google Scholar
Scheider, R., ‘The de Rham realization of the elliptic polylogarithm in families’, PhD Thesis, Universität Regensburg, 2014.Google Scholar
Sprang, J., ‘Eisenstein series via the Poincaré bundle and applications’, PhD Thesis, Universität Regensburg, 2017.Google Scholar
Sprang, J., ‘The algebraic de Rham realization of the elliptic polylogarithm via the Poincarè bundle’, Preprint, 2018, arXiv:1802.04999.Google Scholar
Sprang, J., ‘The syntomic realization of the elliptic polylogarithm via the Poincaré bundle’, Doc. Math. 24 (2019), 1099–1134.Google Scholar
Tsuji, T., ‘Explicit reciprocity law and formal moduli for Lubin–Tate formal groups’, J. Reine Angew. Math. 569 (2004), 103–173.Google Scholar
Urban, E., Nearly Overconvergent Modular Forms, 401–441. (Springer, Berlin, Heidelberg, 2014).Google Scholar