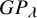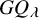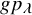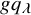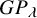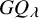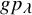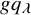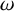1 Introduction
The main results of this paper are to derive explicit combinatorial generating functions for certain families of ‘dual’ power series defined indirectly by Cauchy identities. The formulas that we establish were originally conjectured in [Reference Chiu and Marberg4, Reference Nakagawa and Naruse19]. This introduction gives a very quick summary of the power series involved and the generating functions to be derived. We also explain one application of our formulas to resolve a conjecture of Ikeda and Naruse from [Reference Ikeda and Naruse10].
1.1 Shifted set-valued generating functions
The shifted Young diagram of a strict integer partition
![]() $\lambda = (\lambda _1> \lambda _2 > \dots > \lambda _k>0)$
is the set of pairs
$\lambda = (\lambda _1> \lambda _2 > \dots > \lambda _k>0)$
is the set of pairs
Elements of
![]() $\textsf {SD}_\lambda $
are called positions or boxes. A shifted set-valued tableau of shape
$\textsf {SD}_\lambda $
are called positions or boxes. A shifted set-valued tableau of shape
![]() $\lambda $
is a filling
$\lambda $
is a filling
![]() $T $
of
$T $
of
![]() $\textsf {SD}_{\lambda }$
by finite, nonempty subsets of
$\textsf {SD}_{\lambda }$
by finite, nonempty subsets of
![]() $\tfrac {1}{2}\mathbb {Z}$
. Throughout, we let
$\tfrac {1}{2}\mathbb {Z}$
. Throughout, we let
![]() $ i' := i - \tfrac {1}{2}$
for
$ i' := i - \tfrac {1}{2}$
for
![]() $i \in \mathbb {Z}$
and refer to half-integers as primed numbers .
$i \in \mathbb {Z}$
and refer to half-integers as primed numbers .
Let
![]() $T_{ij}$
denote the entry assigned by T to box
$T_{ij}$
denote the entry assigned by T to box
![]() $(i,j) \in \textsf {SD}_{\lambda }$
, and write
$(i,j) \in \textsf {SD}_{\lambda }$
, and write
![]() $(i,j) \in T$
to indicate that
$(i,j) \in T$
to indicate that
![]() $(i,j) $
is in the domain of T. The diagonal positions of T are the boxes
$(i,j) $
is in the domain of T. The diagonal positions of T are the boxes
![]() $(i,j) \in T$
with
$(i,j) \in T$
with
![]() $i=j$
. A shifted set-valued tableau T is semistandard if all of the following conditions hold:
$i=j$
. A shifted set-valued tableau T is semistandard if all of the following conditions hold:
-
(S1) its entries
 $T_{ij}$
are nonempty finite subsets of
$T_{ij}$
are nonempty finite subsets of
 $\{1'<1<2'<2<\dots \}$
,
$\{1'<1<2'<2<\dots \}$
, -
(S2)
 $\max (T_{ij}) \leq \min (T_{i+1,j})$
and
$\max (T_{ij}) \leq \min (T_{i+1,j})$
and
 $\max (T_{ij}) \leq \min (T_{i,j+1})$
for all relevant
$\max (T_{ij}) \leq \min (T_{i,j+1})$
for all relevant
 $(i,j) \in T$
,
$(i,j) \in T$
, -
(S3) no unprimed number appears in different boxes within the same column, and
-
(S4) no primed number appears in different boxes within the same row.
We draw shifted tableaux in French notation; for example, both

are semistandard shifted set-valued tableaux of shape
![]() $(4, 2, 1)$
. Let
$(4, 2, 1)$
. Let
![]() $\beta , x_1,x_2,x_3,\dots $
be commuting indeterminates. Define
$\beta , x_1,x_2,x_3,\dots $
be commuting indeterminates. Define
![]() $|T| := \sum _{(i,j) \in T} |T_{ij}|$
and
$|T| := \sum _{(i,j) \in T} |T_{ij}|$
and
![]() $\mathbf {x}^T := \prod _i x_i^{a_i+b_i}$
, where
$\mathbf {x}^T := \prod _i x_i^{a_i+b_i}$
, where
![]() $a_i$
and
$a_i$
and
![]() $b_i$
are the number of times that i and
$b_i$
are the number of times that i and
![]() $i'$
appear in the shifted set-valued tableau T, respectively. Our examples above both have
$i'$
appear in the shifted set-valued tableau T, respectively. Our examples above both have
![]() $|T| = 10$
and
$|T| = 10$
and
![]() $\mathbf {x}^T = x_1 x_2^3 x_3^4 x_4 x_5$
. When
$\mathbf {x}^T = x_1 x_2^3 x_3^4 x_4 x_5$
. When
![]() $\lambda $
is a partition (or more generally, any sequence with finite sum), we write
$\lambda $
is a partition (or more generally, any sequence with finite sum), we write
![]() $|\lambda |$
for the sum of its entries.
$|\lambda |$
for the sum of its entries.
Definition 1.1. The K-theoretic Schur P- and Q-functions indexed by a strict partition
![]() $\lambda $
are the formal power series
$\lambda $
are the formal power series
 $$\begin{align*}G\hspace{-0.2mm}P_{\lambda} := \sum_{T \in \mathsf{ShSVT}_P(\lambda)} \beta^{|T|-|\lambda|} \mathbf{x}^{T} \quad\text{and}\quad G\hspace{-0.2mm}Q_{\lambda} := \sum_{T \in \mathsf{ShSVT}_Q(\lambda)} \beta^{|T|-|\lambda|} \mathbf{x}^{T},\end{align*}$$
$$\begin{align*}G\hspace{-0.2mm}P_{\lambda} := \sum_{T \in \mathsf{ShSVT}_P(\lambda)} \beta^{|T|-|\lambda|} \mathbf{x}^{T} \quad\text{and}\quad G\hspace{-0.2mm}Q_{\lambda} := \sum_{T \in \mathsf{ShSVT}_Q(\lambda)} \beta^{|T|-|\lambda|} \mathbf{x}^{T},\end{align*}$$
where
![]() $\mathsf {ShSVT}_Q(\lambda )$
is the set of all semistandard shifted set-valued tableaux of shape
$\mathsf {ShSVT}_Q(\lambda )$
is the set of all semistandard shifted set-valued tableaux of shape
![]() $\lambda $
and
$\lambda $
and
![]() $\mathsf {ShSVT}_P(\lambda )$
is the subset of such tableaux with no primed numbers in any diagonal positions.Footnote
1
$\mathsf {ShSVT}_P(\lambda )$
is the subset of such tableaux with no primed numbers in any diagonal positions.Footnote
1
These expressions belong to ring ![]() . If
. If
![]() $\deg \beta =-1$
, then
$\deg \beta =-1$
, then
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
are homogeneous of degree
$G\hspace {-0.2mm}Q_\lambda $
are homogeneous of degree
![]() $|\lambda |$
, but if
$|\lambda |$
, but if
![]() $\deg \beta =0$
, then the power series have unbounded degree. Both
$\deg \beta =0$
, then the power series have unbounded degree. Both
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
are symmetric in the
$G\hspace {-0.2mm}Q_\lambda $
are symmetric in the
![]() $x_i$
variables [Reference Ikeda and Naruse10, Thm. 9.1]. Setting
$x_i$
variables [Reference Ikeda and Naruse10, Thm. 9.1]. Setting
![]() $\beta =0$
turns
$\beta =0$
turns
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
into the classical Schur P- and Q-functions
$G\hspace {-0.2mm}Q_\lambda $
into the classical Schur P- and Q-functions
![]() $P_\lambda $
and
$P_\lambda $
and
![]() $Q_\lambda $
. It follows that as
$Q_\lambda $
. It follows that as
![]() $\lambda $
ranges over all strict partitions, the sets
$\lambda $
ranges over all strict partitions, the sets
![]() $\{ G\hspace {-0.2mm}P_\lambda \}$
and
$\{ G\hspace {-0.2mm}P_\lambda \}$
and
![]() $\{G\hspace {-0.2mm}Q_\lambda \}$
are linearly independent. While
$\{G\hspace {-0.2mm}Q_\lambda \}$
are linearly independent. While
![]() $Q_\lambda =2^{\ell (\lambda ) }P_\lambda $
, each
$Q_\lambda =2^{\ell (\lambda ) }P_\lambda $
, each
![]() $G\hspace {-0.2mm}Q_\lambda $
is a more complicated but still finite
$G\hspace {-0.2mm}Q_\lambda $
is a more complicated but still finite
![]() $\mathbb {Z}[\beta ]$
-linear combination of
$\mathbb {Z}[\beta ]$
-linear combination of
![]() $G\hspace {-0.2mm}P_\mu $
’s [Reference Chiu and Marberg4, Thm. 1.1].
$G\hspace {-0.2mm}P_\mu $
’s [Reference Chiu and Marberg4, Thm. 1.1].
Ikeda and Naruse first introduced these symmetric functions in [Reference Ikeda and Naruse10] for applications in geometry. Specializations of
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
represent the structure sheaves of Schubert varieties in the torus equivariant K-theory of the maximal isotropic Grassmannians of orthogonal and symplectic types [Reference Ikeda and Naruse10, Cor. 8.1]; see also [Reference Nakagawa and Naruse18, Reference Nakagawa and Naruse19, Reference Naruse20]. These power series further appear as ‘stable limits’ of K-theory classes of certain orbit closures in the type A flag variety [Reference Marberg and Pawlowski16, Reference Marberg and Pawlowski17].
$G\hspace {-0.2mm}Q_\lambda $
represent the structure sheaves of Schubert varieties in the torus equivariant K-theory of the maximal isotropic Grassmannians of orthogonal and symplectic types [Reference Ikeda and Naruse10, Cor. 8.1]; see also [Reference Nakagawa and Naruse18, Reference Nakagawa and Naruse19, Reference Naruse20]. These power series further appear as ‘stable limits’ of K-theory classes of certain orbit closures in the type A flag variety [Reference Marberg and Pawlowski16, Reference Marberg and Pawlowski17].
1.2 Dual functions via Cauchy identities
Our main results concern the following dual forms of
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
.
$G\hspace {-0.2mm}Q_\lambda $
.
Definition 1.2. The dual K-theoretic Schur P- and Q-functions
![]() $g\hspace {-0.1mm}p_\lambda $
and
$g\hspace {-0.1mm}p_\lambda $
and
![]() $g\hspace {-0.1mm}q_\lambda $
are the unique elements of
$g\hspace {-0.1mm}q_\lambda $
are the unique elements of ![]() indexed by strict partitions
indexed by strict partitions
![]() $\lambda $
satisfying the Cauchy identities
$\lambda $
satisfying the Cauchy identities
 $$ \begin{align} \sum_\lambda G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) g\hspace{-0.1mm}p_\lambda(\mathbf{y}) = \sum_\lambda G\hspace{-0.2mm}P_\lambda(\mathbf{x}) g\hspace{-0.1mm}q_\lambda(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{ 1 - \overline{x_i} y_j}{1-x_iy_j}, \end{align} $$
$$ \begin{align} \sum_\lambda G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) g\hspace{-0.1mm}p_\lambda(\mathbf{y}) = \sum_\lambda G\hspace{-0.2mm}P_\lambda(\mathbf{x}) g\hspace{-0.1mm}q_\lambda(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{ 1 - \overline{x_i} y_j}{1-x_iy_j}, \end{align} $$
where we set
![]() $\overline {x} := \tfrac {-x}{1+\beta x}$
.
$\overline {x} := \tfrac {-x}{1+\beta x}$
.
The power series
![]() $g\hspace {-0.1mm}p_{\lambda }$
and
$g\hspace {-0.1mm}p_{\lambda }$
and
![]() $g\hspace {-0.1mm}q_{\lambda }$
are special cases of Nakagawa and Naruse’s dual universal factorial Schur P- and Q-functions, which are defined via a more general version of (1.1) [Reference Nakagawa and Naruse19, Def. 3.2]. Both
$g\hspace {-0.1mm}q_{\lambda }$
are special cases of Nakagawa and Naruse’s dual universal factorial Schur P- and Q-functions, which are defined via a more general version of (1.1) [Reference Nakagawa and Naruse19, Def. 3.2]. Both
![]() $\{g\hspace {-0.1mm}p_\lambda \}$
and
$\{g\hspace {-0.1mm}p_\lambda \}$
and
![]() $\{g\hspace {-0.1mm}q_\lambda \}$
are linearly independent families of functions that are symmetric in the
$\{g\hspace {-0.1mm}q_\lambda \}$
are linearly independent families of functions that are symmetric in the
![]() $x_i$
variables and homogeneous if
$x_i$
variables and homogeneous if
![]() $\deg \beta = 1$
[Reference Nakagawa and Naruse19, Thm. 3.1]. These properties let one define the following conjugate symmetric functions, which were first considered in [Reference Chiu and Marberg4]:
$\deg \beta = 1$
[Reference Nakagawa and Naruse19, Thm. 3.1]. These properties let one define the following conjugate symmetric functions, which were first considered in [Reference Chiu and Marberg4]:
Definition 1.3. Write
![]() $\omega $
for the
$\omega $
for the
![]() $\mathbb {Z}[\beta ]$
-linear involution of the ring of symmetric functions (in the variables
$\mathbb {Z}[\beta ]$
-linear involution of the ring of symmetric functions (in the variables
![]() $x_1,x_2,\dots $
with coefficients in
$x_1,x_2,\dots $
with coefficients in
![]() $\mathbb {Z}[\beta ]$
) acting on Schur functions as
$\mathbb {Z}[\beta ]$
) acting on Schur functions as
![]() $\omega (s_\lambda ) = s_{\lambda ^\top }$
. The conjugate dual K-theoretic Schur P- and Q-functions of a strict partition
$\omega (s_\lambda ) = s_{\lambda ^\top }$
. The conjugate dual K-theoretic Schur P- and Q-functions of a strict partition
![]() $\lambda $
are
$\lambda $
are
![]() $ j\hspace {-0.1mm}p_\lambda := \omega (g\hspace {-0.1mm}p_\lambda )$
and
$ j\hspace {-0.1mm}p_\lambda := \omega (g\hspace {-0.1mm}p_\lambda )$
and
![]() $ j\hspace {-0.1mm}q_\lambda := \omega (g\hspace {-0.1mm}q_\lambda ).$
$ j\hspace {-0.1mm}q_\lambda := \omega (g\hspace {-0.1mm}q_\lambda ).$
1.3 Shifted plane partition generating functions
Our first main result is a generating function formula for
![]() $g\hspace {-0.1mm}p_\lambda $
and
$g\hspace {-0.1mm}p_\lambda $
and
![]() $g\hspace {-0.1mm}q_\lambda $
that was predicted in [Reference Nakagawa and Naruse19]. Let
$g\hspace {-0.1mm}q_\lambda $
that was predicted in [Reference Nakagawa and Naruse19]. Let
![]() $ \lambda $
be a strict partition. A shifted plane partition of shape
$ \lambda $
be a strict partition. A shifted plane partition of shape
![]() $\lambda $
is a filling of
$\lambda $
is a filling of
![]() $\textsf {SD}_{\lambda }$
by elements of
$\textsf {SD}_{\lambda }$
by elements of
![]() $ \{1'<1<2'<2<\dots \}$
with weakly increasing rows and columns. Examples include
$ \{1'<1<2'<2<\dots \}$
with weakly increasing rows and columns. Examples include

which both have shape
![]() $(5,3,2,1)$
. Given such a filling T, let
$(5,3,2,1)$
. Given such a filling T, let
![]() $c_i$
be the number of distinct columns of T containing i, and let
$c_i$
be the number of distinct columns of T containing i, and let
![]() $r_i$
be the number of distinct rows of T containing
$r_i$
be the number of distinct rows of T containing
![]() $i'$
. Define
$i'$
. Define
Both examples above have
![]() $|{\operatorname {wt}}_{ {\mathrm {PP}}}(T)| =9$
and
$|{\operatorname {wt}}_{ {\mathrm {PP}}}(T)| =9$
and
![]() $\mathbf {x}^{\operatorname {wt}_{ {\mathrm {PP}}}(T)} = x_1^4 x_2^3x_3x_5$
.
$\mathbf {x}^{\operatorname {wt}_{ {\mathrm {PP}}}(T)} = x_1^4 x_2^3x_3x_5$
.
Theorem 1.4. Let
![]() $ \mathsf {ShPP}_Q(\lambda )$
be the set of all shifted plane partitions of shape
$ \mathsf {ShPP}_Q(\lambda )$
be the set of all shifted plane partitions of shape
![]() $\lambda $
, and define
$\lambda $
, and define
![]() $ \mathsf {ShPP}_P(\lambda )$
to be the subset of such fillings with no unprimed diagonal entries. Then
$ \mathsf {ShPP}_P(\lambda )$
to be the subset of such fillings with no unprimed diagonal entries. Then
 $$ \begin{align*} g\hspace{-0.1mm}p_{\lambda} = \sum_{T\in {\mathsf{ShPP}}_P(\lambda)} (-\beta)^{|\lambda| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{x}^{\operatorname{wt}_{\mathrm{PP}(T)}} \text{ and } g\hspace{-0.1mm}q_{\lambda} = \sum_{T\in {\mathsf{ShPP}}_Q(\lambda)} (-\beta)^{|\lambda| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{x}^{\operatorname{wt}_{\mathrm{PP}(T)}}. \end{align*} $$
$$ \begin{align*} g\hspace{-0.1mm}p_{\lambda} = \sum_{T\in {\mathsf{ShPP}}_P(\lambda)} (-\beta)^{|\lambda| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{x}^{\operatorname{wt}_{\mathrm{PP}(T)}} \text{ and } g\hspace{-0.1mm}q_{\lambda} = \sum_{T\in {\mathsf{ShPP}}_Q(\lambda)} (-\beta)^{|\lambda| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{x}^{\operatorname{wt}_{\mathrm{PP}(T)}}. \end{align*} $$
This result was conjectured by Nakagawa and Naruse as [Reference Nakagawa and Naruse19, Conj. 5.1]. We will actually prove a more general formula for the skew versions of
![]() $g\hspace {-0.1mm}p_\lambda $
and
$g\hspace {-0.1mm}p_\lambda $
and
![]() $g\hspace {-0.1mm}q_\lambda $
; see Theorem 4.24. These formulas make it possible to compute the terms in
$g\hspace {-0.1mm}q_\lambda $
; see Theorem 4.24. These formulas make it possible to compute the terms in
![]() $g\hspace {-0.1mm}p_\lambda $
and
$g\hspace {-0.1mm}p_\lambda $
and
![]() $g\hspace {-0.1mm}q_\lambda $
, which is not straightforward from (1.1).
$g\hspace {-0.1mm}q_\lambda $
, which is not straightforward from (1.1).
1.4 Shifted bar tableaux generating functions
Our second main result is a generating function formula for
![]() $j\hspace {-0.1mm}p_\lambda $
and
$j\hspace {-0.1mm}p_\lambda $
and
![]() $j\hspace {-0.1mm}q_\lambda $
that was predicted in [Reference Chiu and Marberg4]. Continue to let
$j\hspace {-0.1mm}q_\lambda $
that was predicted in [Reference Chiu and Marberg4]. Continue to let
![]() $\lambda $
be a strict integer partition. Suppose V is a shifted tableauFootnote
2
of shape
$\lambda $
be a strict integer partition. Suppose V is a shifted tableauFootnote
2
of shape
![]() $\lambda $
with no unprimed entries repeated in any column and no primed entries repeated in any row. Let
$\lambda $
with no unprimed entries repeated in any column and no primed entries repeated in any row. Let
![]() $\Pi $
be a partition of the diagram
$\Pi $
be a partition of the diagram
![]() $\textsf {SD}_{\lambda }$
into (disjoint, nonempty) subsets of adjacent boxes containing the same entry in V. Each block of
$\textsf {SD}_{\lambda }$
into (disjoint, nonempty) subsets of adjacent boxes containing the same entry in V. Each block of
![]() $ \Pi $
is a contiguous ‘bar’ of positions in the same row or column, and we refer to the pair
$ \Pi $
is a contiguous ‘bar’ of positions in the same row or column, and we refer to the pair
![]() $T=(V,\Pi )$
as a shifted bar tableau of shape
$T=(V,\Pi )$
as a shifted bar tableau of shape
![]() $\lambda $
.
$\lambda $
.
If V is semistandard in the sense of having weakly increasing rows and columns, then we say that T is also semistandard. We draw shifted bar tableaux as pictures like

to represent

These objects are the shifted analogues of what are called valued-set tableaux in [Reference Lam and Pylyavskyy11]. The word ‘valued-set’ is just a formal transposition of ‘set-valued’; we believe that the name ‘bar tableau’ is more intuitive and descriptive.
Given a shifted bar tableau
![]() $T=(V,\Pi )$
, let
$T=(V,\Pi )$
, let
![]() $ |T| := |\Pi |$
and
$ |T| := |\Pi |$
and
![]() $ \mathbf {x}^T := \prod _{i\geq 1} x_i^{b_i}$
, where
$ \mathbf {x}^T := \prod _{i\geq 1} x_i^{b_i}$
, where
![]() $b_i$
is the number of blocks in
$b_i$
is the number of blocks in
![]() $\Pi $
containing i or
$\Pi $
containing i or
![]() $i'$
. Our example above has
$i'$
. Our example above has
![]() $|T| = 5$
and
$|T| = 5$
and
![]() $\mathbf {x}^T = x_1^2 x_2 x_3^2$
.
$\mathbf {x}^T = x_1^2 x_2 x_3^2$
.
Theorem 1.5. Let
![]() $\mathsf {ShBT}_Q(\lambda )$
denote the set of all semistandard shifted bar tableaux of shape
$\mathsf {ShBT}_Q(\lambda )$
denote the set of all semistandard shifted bar tableaux of shape
![]() $\lambda $
, and let
$\lambda $
, and let
![]() $\mathsf {ShBT}_P(\lambda )$
be the subset of such tableaux with no primed diagonal entries. Then
$\mathsf {ShBT}_P(\lambda )$
be the subset of such tableaux with no primed diagonal entries. Then
 $$\begin{align*}\begin{aligned} j\hspace{-0.1mm}p_{\lambda} = \sum_{T\in \mathsf{ShBT}_P(\lambda)} (-\beta)^{|\lambda|-|T|} \mathbf{x}^{T} \quad\mathrm{and}\quad j\hspace{-0.1mm}q_{\lambda} = \sum_{T\in \mathsf{ShBT}_Q(\lambda)} (-\beta)^{|\lambda| -|T|} \mathbf{x}^{T}{\kern-1.5pt}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} j\hspace{-0.1mm}p_{\lambda} = \sum_{T\in \mathsf{ShBT}_P(\lambda)} (-\beta)^{|\lambda|-|T|} \mathbf{x}^{T} \quad\mathrm{and}\quad j\hspace{-0.1mm}q_{\lambda} = \sum_{T\in \mathsf{ShBT}_Q(\lambda)} (-\beta)^{|\lambda| -|T|} \mathbf{x}^{T}{\kern-1.5pt}. \end{aligned} \end{align*}$$
This result was conjectured by Chiu and the second author as [Reference Chiu and Marberg4, Conj. 7.2]. We will actually prove a more general formula for the skew versions of
![]() $j\hspace {-0.1mm}p_\lambda $
and
$j\hspace {-0.1mm}p_\lambda $
and
![]() $j\hspace {-0.1mm}q_\lambda $
; see Theorems 4.13 and 4.20.
$j\hspace {-0.1mm}q_\lambda $
; see Theorems 4.13 and 4.20.
1.5 Application to conjectures of Ikeda and Naruse
Consider the modules consisting of all infinite
![]() $\mathbb {Z}[\beta ]$
-linear combinations of the functions
$\mathbb {Z}[\beta ]$
-linear combinations of the functions
![]() $\{ G\hspace {-0.2mm}P_\lambda \}$
and
$\{ G\hspace {-0.2mm}P_\lambda \}$
and
![]() $\{G\hspace {-0.2mm}Q_\lambda \}$
, with
$\{G\hspace {-0.2mm}Q_\lambda \}$
, with
![]() $\lambda $
ranging over all strict partitions. Ikeda and Naruse proved that these modules are both rings [Reference Ikeda and Naruse10, Props. 3.4 and 3.5]. Concretely, this means that
$\lambda $
ranging over all strict partitions. Ikeda and Naruse proved that these modules are both rings [Reference Ikeda and Naruse10, Props. 3.4 and 3.5]. Concretely, this means that
![]() $G\hspace {-0.2mm}P_\lambda G\hspace {-0.2mm}P_\mu $
(respectively,
$G\hspace {-0.2mm}P_\lambda G\hspace {-0.2mm}P_\mu $
(respectively,
![]() $G\hspace {-0.2mm}Q_\lambda G\hspace {-0.2mm}Q_\mu $
) always expands as a (possibly infinite)
$G\hspace {-0.2mm}Q_\lambda G\hspace {-0.2mm}Q_\mu $
) always expands as a (possibly infinite)
![]() $\mathbb {Z}[\beta ]$
-linear combination of
$\mathbb {Z}[\beta ]$
-linear combination of
![]() $G\hspace {-0.2mm}P_\nu $
’s (respectively,
$G\hspace {-0.2mm}P_\nu $
’s (respectively,
![]() $G\hspace {-0.2mm}Q_\nu $
’s).
$G\hspace {-0.2mm}Q_\nu $
’s).
Ikeda and Naruse conjectured that these expansions are actually finite [Reference Ikeda and Naruse10, Conj. 3.1 and 3.2]. For the
![]() $G\hspace {-0.2mm}P$
-functions, this stronger ring property was established by Clifford, Thomas and Yong in [Reference Clifford, Thomas and Yong5]; other proofs have subsequently been given in [Reference Hamaker, Keilthy, Patrias, Webster, Zhang and Zhou9, §4], [Reference Marberg15, §1.2] and [Reference Pechenik and Yong21, §8]. The problem of showing the same property for the
$G\hspace {-0.2mm}P$
-functions, this stronger ring property was established by Clifford, Thomas and Yong in [Reference Clifford, Thomas and Yong5]; other proofs have subsequently been given in [Reference Hamaker, Keilthy, Patrias, Webster, Zhang and Zhou9, §4], [Reference Marberg15, §1.2] and [Reference Pechenik and Yong21, §8]. The problem of showing the same property for the
![]() $G\hspace {-0.2mm}Q$
-functions appears to still be open. Building on [Reference Chiu and Marberg4], we are able to resolve this problem:
$G\hspace {-0.2mm}Q$
-functions appears to still be open. Building on [Reference Chiu and Marberg4], we are able to resolve this problem:
Theorem 1.6. The free
![]() $\mathbb {Z}[\beta ]$
-modules with bases
$\mathbb {Z}[\beta ]$
-modules with bases
![]() $\{ G\hspace {-0.2mm}P_\lambda \}$
and
$\{ G\hspace {-0.2mm}P_\lambda \}$
and
![]() $\{G\hspace {-0.2mm}Q_\lambda \}$
(where
$\{G\hspace {-0.2mm}Q_\lambda \}$
(where
![]() $\lambda $
ranges over all strict partitions) are subrings of
$\lambda $
ranges over all strict partitions) are subrings of ![]() . If
. If
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
are strict partitions, then
$\mu $
are strict partitions, then
for integer coefficients
![]() $a_{\lambda \mu }^\nu $
and
$a_{\lambda \mu }^\nu $
and
![]() $ b_{\lambda \mu }^\nu $
that are
$ b_{\lambda \mu }^\nu $
that are
-
(a) nonzero for only finitely many strict partitions
 $\nu $
,
$\nu $
, -
(b) zero whenever
 $|\nu | < |\lambda | + |\mu |$
or
$|\nu | < |\lambda | + |\mu |$
or
 $\ell (\nu )> \ell (\lambda ) + \ell (\mu )$
and
$\ell (\nu )> \ell (\lambda ) + \ell (\mu )$
and -
(c) nonnegative.
Proof. The ring property for the span of the
![]() $G\hspace {-0.2mm}P$
-functions follows from [Reference Clifford, Thomas and Yong5]. Meanwhile, [Reference Chiu and Marberg4, Cor. 7.7] is exactly the assertion that the ring property for the span of the
$G\hspace {-0.2mm}P$
-functions follows from [Reference Clifford, Thomas and Yong5]. Meanwhile, [Reference Chiu and Marberg4, Cor. 7.7] is exactly the assertion that the ring property for the span of the
![]() $G\hspace {-0.2mm}Q$
-functions follows from Theorem 1.5 (or more precisely from its skew version, which is Theorem 4.20). These properties assert that the products
$G\hspace {-0.2mm}Q$
-functions follows from Theorem 1.5 (or more precisely from its skew version, which is Theorem 4.20). These properties assert that the products
![]() $G\hspace {-0.2mm}P_\lambda G\hspace {-0.2mm}P_\mu $
and
$G\hspace {-0.2mm}P_\lambda G\hspace {-0.2mm}P_\mu $
and
![]() $G\hspace {-0.2mm}Q_\lambda G\hspace {-0.2mm}Q_\mu $
expand in the respective bases with coefficients in
$G\hspace {-0.2mm}Q_\lambda G\hspace {-0.2mm}Q_\mu $
expand in the respective bases with coefficients in
![]() $\mathbb {Z}[\beta ]$
satisfying (a). Taking
$\mathbb {Z}[\beta ]$
satisfying (a). Taking
![]() $\deg \beta = -1$
, the homogeneity of the
$\deg \beta = -1$
, the homogeneity of the
![]() $G\hspace {-0.2mm}P$
- and
$G\hspace {-0.2mm}P$
- and
![]() $G\hspace {-0.2mm}Q$
-functions implies that, in fact, the coefficient of
$G\hspace {-0.2mm}Q$
-functions implies that, in fact, the coefficient of
![]() $G\hspace {-0.2mm}P_\nu $
(respectively,
$G\hspace {-0.2mm}P_\nu $
(respectively,
![]() $G\hspace {-0.2mm}Q_\nu $
) must be of the form
$G\hspace {-0.2mm}Q_\nu $
) must be of the form
![]() $a_{\lambda \mu }^\nu \beta ^{|\nu | - |\lambda | - |\mu |}$
(respectively,
$a_{\lambda \mu }^\nu \beta ^{|\nu | - |\lambda | - |\mu |}$
(respectively,
![]() $b_{\lambda \mu }^\nu \beta ^{|\nu | - |\lambda | - |\mu |}$
) for an integer
$b_{\lambda \mu }^\nu \beta ^{|\nu | - |\lambda | - |\mu |}$
) for an integer
![]() $a_{\lambda \mu }^\nu $
(respectively,
$a_{\lambda \mu }^\nu $
(respectively,
![]() $b_{\lambda \mu }^\nu $
), and moreover that
$b_{\lambda \mu }^\nu $
), and moreover that
![]() $a_{\lambda \mu }^\nu = b_{\lambda \mu }^\nu = 0$
whenever
$a_{\lambda \mu }^\nu = b_{\lambda \mu }^\nu = 0$
whenever
![]() $|\nu | < |\lambda | + |\mu |$
. Given our main results (namely, Theorems 4.13 and 4.20), [Reference Chiu and Marberg4, Thm. 7.6] asserts that
$|\nu | < |\lambda | + |\mu |$
. Given our main results (namely, Theorems 4.13 and 4.20), [Reference Chiu and Marberg4, Thm. 7.6] asserts that
![]() $a_{\lambda \mu }^\nu = b_{\lambda \mu }^\nu =0$
whenever
$a_{\lambda \mu }^\nu = b_{\lambda \mu }^\nu =0$
whenever
![]() $\ell (\nu )> \ell (\lambda ) + \ell (\mu )$
.
$\ell (\nu )> \ell (\lambda ) + \ell (\mu )$
.
Given Ikeda and Naruse’s interpretation of
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
as K-theory representatives for Schubert varieties in the orthogonal and Lagrangian Grassmannians, the fact that
$G\hspace {-0.2mm}Q_\lambda $
as K-theory representatives for Schubert varieties in the orthogonal and Lagrangian Grassmannians, the fact that
![]() $a_{\lambda \mu }^\nu $
and
$a_{\lambda \mu }^\nu $
and
![]() $ b_{\lambda \mu }^\nu $
are nonnegative can be deduced from a result of Brion [Reference Brion1]. We only explain this for the
$ b_{\lambda \mu }^\nu $
are nonnegative can be deduced from a result of Brion [Reference Brion1]. We only explain this for the
![]() $b_{\lambda \mu }^\nu $
coefficients, since
$b_{\lambda \mu }^\nu $
coefficients, since
![]() $a_{\lambda \mu }^\nu \geq 0$
follows directly from [Reference Clifford, Thomas and Yong5, Thm. 1.2].
$a_{\lambda \mu }^\nu \geq 0$
follows directly from [Reference Clifford, Thomas and Yong5, Thm. 1.2].
As summarized in [Reference Ikeda and Naruse10, §8.1], for each strict partition
![]() $\lambda \subseteq (n,\dots ,3,2,1)$
there is an associated Schubert variety
$\lambda \subseteq (n,\dots ,3,2,1)$
there is an associated Schubert variety
![]() $\Omega _\lambda $
in the Lagrangian Grassmannian
$\Omega _\lambda $
in the Lagrangian Grassmannian
![]() $\mathcal {G}_n := LG(n)$
. The variety
$\mathcal {G}_n := LG(n)$
. The variety
![]() $\Omega _\lambda $
is closed with codimension
$\Omega _\lambda $
is closed with codimension
![]() $|\lambda |$
, and its structure sheaf
$|\lambda |$
, and its structure sheaf
![]() $\mathcal {O}_{\Omega _\lambda }$
defines a class
$\mathcal {O}_{\Omega _\lambda }$
defines a class
![]() $[\mathcal {O}_{\Omega _\lambda }]$
in the K-theory ring
$[\mathcal {O}_{\Omega _\lambda }]$
in the K-theory ring
![]() $K(\mathcal {G}_n)$
of coherent sheaves on
$K(\mathcal {G}_n)$
of coherent sheaves on
![]() $\mathcal {G}_n$
. These classes are an additive basis for
$\mathcal {G}_n$
. These classes are an additive basis for
![]() $K(\mathcal {G}_n)$
, and so we have
$K(\mathcal {G}_n)$
, and so we have
![]() $ [\mathcal {O}_{\Omega _\lambda }] [\mathcal {O}_{\Omega _\mu }] = \sum _\nu (-1)^{|\nu | - |\lambda |-|\mu |} c_{\lambda \mu }^\nu [\mathcal {O}_{\Omega _\nu }]$
for some integers
$ [\mathcal {O}_{\Omega _\lambda }] [\mathcal {O}_{\Omega _\mu }] = \sum _\nu (-1)^{|\nu | - |\lambda |-|\mu |} c_{\lambda \mu }^\nu [\mathcal {O}_{\Omega _\nu }]$
for some integers
![]() $c_{\lambda \mu }^\nu \in \mathbb {Z}$
. The main result of [Reference Brion1] shows that the coefficients
$c_{\lambda \mu }^\nu \in \mathbb {Z}$
. The main result of [Reference Brion1] shows that the coefficients
![]() $c_{\lambda \mu }^\nu $
are nonnegative. (In fact, the main result of [Reference Brion1] is a more general statement that applies to Schubert varieties in any complex flag variety.)
$c_{\lambda \mu }^\nu $
are nonnegative. (In fact, the main result of [Reference Brion1] is a more general statement that applies to Schubert varieties in any complex flag variety.)
If we set
![]() $\beta =-1$
and define
$\beta =-1$
and define
![]() $\mathit {G\Gamma }_{n,+}$
to be the
$\mathit {G\Gamma }_{n,+}$
to be the
![]() $\mathbb {Z}$
-span of all polynomials
$\mathbb {Z}$
-span of all polynomials
![]() $G\hspace {-0.2mm}Q_\lambda (x_1,\dots ,x_n)$
with
$G\hspace {-0.2mm}Q_\lambda (x_1,\dots ,x_n)$
with
![]() $\ell (\lambda ) \leq n$
, then there is a surjective ring homomorphism
$\ell (\lambda ) \leq n$
, then there is a surjective ring homomorphism
![]() $\mathit {G\Gamma }_{n,+} \to K(\mathcal {G}_n)$
sending
$\mathit {G\Gamma }_{n,+} \to K(\mathcal {G}_n)$
sending
![]() $G\hspace {-0.2mm}Q_\lambda (x_1,\dots ,x_n) $
to
$G\hspace {-0.2mm}Q_\lambda (x_1,\dots ,x_n) $
to
![]() $ [\mathcal {O}_{\Omega _\lambda }]$
if
$ [\mathcal {O}_{\Omega _\lambda }]$
if
![]() $\lambda \subseteq (n,\dots ,3,2,1)$
and to zero otherwise [Reference Ikeda and Naruse10, Cor. 8.1]. If n is large enough that
$\lambda \subseteq (n,\dots ,3,2,1)$
and to zero otherwise [Reference Ikeda and Naruse10, Cor. 8.1]. If n is large enough that
![]() $(n, \ldots , 3, 2, 1)$
contains both
$(n, \ldots , 3, 2, 1)$
contains both
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
as well as the finite number of strict partitions
$\mu $
as well as the finite number of strict partitions
![]() $\nu $
with
$\nu $
with
![]() $b_{\lambda \mu }^\nu \neq 0$
, then it follows that
$b_{\lambda \mu }^\nu \neq 0$
, then it follows that
![]() $ [\mathcal {O}_{\Omega _\lambda }] [\mathcal {O}_{\Omega _\mu }] = \sum _\nu (-1)^{|\nu | - |\lambda |-|\mu |} b_{\lambda \mu }^\nu [\mathcal {O}_{\Omega _\nu }]$
, and so
$ [\mathcal {O}_{\Omega _\lambda }] [\mathcal {O}_{\Omega _\mu }] = \sum _\nu (-1)^{|\nu | - |\lambda |-|\mu |} b_{\lambda \mu }^\nu [\mathcal {O}_{\Omega _\nu }]$
, and so
![]() $b_{\lambda \mu }^\nu = c_{\lambda \mu }^\nu \geq 0$
.
$b_{\lambda \mu }^\nu = c_{\lambda \mu }^\nu \geq 0$
.
Remark . The subsets of
![]() $\mathbb {Z}[\beta ][x_1,\dots ,x_n]$
given by
$\mathbb {Z}[\beta ][x_1,\dots ,x_n]$
given by
are each linearly independent over
![]() $\mathbb {Z}[\beta ]$
by [Reference Ikeda and Naruse10, Thm. 3.1 and Prop. 3.2], and the expansion of
$\mathbb {Z}[\beta ]$
by [Reference Ikeda and Naruse10, Thm. 3.1 and Prop. 3.2], and the expansion of
![]() $G\hspace {-0.2mm}Q_\lambda (x_1,\dots ,x_n) G\hspace {-0.2mm}Q_\mu (x_1,\dots ,x_n)$
into
$G\hspace {-0.2mm}Q_\lambda (x_1,\dots ,x_n) G\hspace {-0.2mm}Q_\mu (x_1,\dots ,x_n)$
into
![]() $G\hspace {-0.2mm}Q_\nu (x_1,\dots ,x_n)$
’s can be calculated by a finite linear algebra computation. Theorem 1.6 implies that if
$G\hspace {-0.2mm}Q_\nu (x_1,\dots ,x_n)$
’s can be calculated by a finite linear algebra computation. Theorem 1.6 implies that if
![]() $\ell (\lambda ) + \ell (\mu ) \leq n$
, then the same finite computation completely determines the expansion of
$\ell (\lambda ) + \ell (\mu ) \leq n$
, then the same finite computation completely determines the expansion of
![]() $G\hspace {-0.2mm}Q_\lambda G\hspace {-0.2mm}Q_\mu $
into
$G\hspace {-0.2mm}Q_\lambda G\hspace {-0.2mm}Q_\mu $
into
![]() $G\hspace {-0.2mm}Q_\nu $
’s, and likewise for the
$G\hspace {-0.2mm}Q_\nu $
’s, and likewise for the
![]() $G\hspace {-0.2mm}P$
-functions.
$G\hspace {-0.2mm}P$
-functions.
The proof of [Reference Chiu and Marberg4, Cor. 7.7], with minor changes, would also show that our generating function for
![]() $j\hspace {-0.1mm}q_\lambda $
implies the ring property for
$j\hspace {-0.1mm}q_\lambda $
implies the ring property for
![]() . However, this nonconstructive argument is less informative than [Reference Clifford, Thomas and Yong5, Thm. 1.2], which gives an explicit Littlewood–Richardson rule for products of
. However, this nonconstructive argument is less informative than [Reference Clifford, Thomas and Yong5, Thm. 1.2], which gives an explicit Littlewood–Richardson rule for products of
![]() $G\hspace {-0.2mm}P$
-functions. It is an open problem to find such a rule for the
$G\hspace {-0.2mm}P$
-functions. It is an open problem to find such a rule for the
![]() $G\hspace {-0.2mm}Q$
-functions, as well as for the
$G\hspace {-0.2mm}Q$
-functions, as well as for the
![]() $g\hspace {-0.1mm}p$
- and
$g\hspace {-0.1mm}p$
- and
![]() $g\hspace {-0.1mm}q$
-functions, which span two other subrings of symmetric functions.
$g\hspace {-0.1mm}q$
-functions, which span two other subrings of symmetric functions.
1.6 Comparison with unshifted versions
Our main results are shifted analogues of ‘classical’ theorems that we summarize here for comparison. The Young diagram of a partition
![]() $\lambda = (\lambda _1 \geq \lambda _2 \geq \dots \geq \lambda _k>0)$
is the set of positions
$\lambda = (\lambda _1 \geq \lambda _2 \geq \dots \geq \lambda _k>0)$
is the set of positions
![]() $\textsf {D}_\lambda = \{ (i,j) \in [k]\times \mathbb {Z} : 1 \leq j \leq \lambda _i\}$
. An (unshifted) semistandard set-valued tableau of shape
$\textsf {D}_\lambda = \{ (i,j) \in [k]\times \mathbb {Z} : 1 \leq j \leq \lambda _i\}$
. An (unshifted) semistandard set-valued tableau of shape
![]() $\lambda $
is defined in the same way as the analogous shifted object, except that such a tableau is a filling of
$\lambda $
is defined in the same way as the analogous shifted object, except that such a tableau is a filling of
![]() $\textsf {D}_\lambda $
by finite nonempty subsets of
$\textsf {D}_\lambda $
by finite nonempty subsets of
![]() $\{1<2<3<\dots \}$
rather than
$\{1<2<3<\dots \}$
rather than
![]() $\{1'<1<2'<2<\dots \}$
.
$\{1'<1<2'<2<\dots \}$
.
Definition 1.7. Write
![]() $\mathsf {SVT}(\lambda )$
for the set of semistandard set-valued tableaux of shape
$\mathsf {SVT}(\lambda )$
for the set of semistandard set-valued tableaux of shape
![]() $\lambda $
. Then the stable Grothendieck polynomial of
$\lambda $
. Then the stable Grothendieck polynomial of
![]() $\lambda $
is the formal power series
$\lambda $
is the formal power series
Definition 1.8. The dual stable Grothendieck polynomials
![]() $g_\lambda $
are the unique formal power series in
$g_\lambda $
are the unique formal power series in ![]() indexed by integer partitions
indexed by integer partitions
![]() $\lambda $
satisfying the Cauchy identity
$\lambda $
satisfying the Cauchy identity
 $$\begin{align*}\sum_\lambda G_\lambda(\mathbf{x}) g_\lambda(\mathbf{y}) = \sum_\lambda s_\lambda(\mathbf{x}) s_\lambda(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{ 1}{1-x_iy_j}.\end{align*}$$
$$\begin{align*}\sum_\lambda G_\lambda(\mathbf{x}) g_\lambda(\mathbf{y}) = \sum_\lambda s_\lambda(\mathbf{x}) s_\lambda(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{ 1}{1-x_iy_j}.\end{align*}$$
Definition 1.9. The conjugate dual stable Grothendieck polynomial of
![]() $\lambda $
is
$\lambda $
is
![]() $ j_\lambda := \omega (g_{\lambda ^\top }).$
$ j_\lambda := \omega (g_{\lambda ^\top }).$
All three families
![]() $\{ G_\lambda \}$
,
$\{ G_\lambda \}$
,
![]() $\{g_\lambda \}$
and
$\{g_\lambda \}$
and
![]() $\{ j_\lambda \}$
are linearly independent symmetric functions which coincide with the usual Schur functions
$\{ j_\lambda \}$
are linearly independent symmetric functions which coincide with the usual Schur functions
![]() $\{ s_\lambda \}$
when
$\{ s_\lambda \}$
when
![]() $\beta =0$
[Reference Buch2, Reference Lam and Pylyavskyy11]. Our definition of
$\beta =0$
[Reference Buch2, Reference Lam and Pylyavskyy11]. Our definition of
![]() $j_\lambda $
involves a transposition of indices compared to [Reference Lam and Pylyavskyy11, §9.8]; this convention ensures that
$j_\lambda $
involves a transposition of indices compared to [Reference Lam and Pylyavskyy11, §9.8]; this convention ensures that
![]() $j_\lambda |_{\beta =0} = s_\lambda $
.
$j_\lambda |_{\beta =0} = s_\lambda $
.
We define (unshifted) plane partitions and semistandard bar tableaux of shape
![]() $\lambda $
in the same way as our shifted versions, except the relevant objects are fillings of
$\lambda $
in the same way as our shifted versions, except the relevant objects are fillings of
![]() $\textsf {D}_\lambda $
by positive integers (excluding primed numbers). Let
$\textsf {D}_\lambda $
by positive integers (excluding primed numbers). Let
![]() $\mathsf {PP}(\lambda )$
be the set of plane partitions of shape
$\mathsf {PP}(\lambda )$
be the set of plane partitions of shape
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\mathsf {BT}(\lambda )$
be the set of semistandard bar tableaux of shape
$\mathsf {BT}(\lambda )$
be the set of semistandard bar tableaux of shape
![]() $\lambda $
; these objects are called valued-set tableaux in [Reference Lam and Pylyavskyy11, §9].
$\lambda $
; these objects are called valued-set tableaux in [Reference Lam and Pylyavskyy11, §9].
Theorem 1.10 Lam and Pylyavskyy [Reference Lam and Pylyavskyy11, §9].
For all partitions
![]() $\lambda $
, it holds that
$\lambda $
, it holds that
The stable Grothendieck polynomials
![]() $G_\lambda $
were introduced in Fomin and Kirillov’s paper [Reference Fomin and Kirillov6] as certain limits of Lascoux and Schützenberger’s Grothendieck polynomials [Reference Lascoux and Schützenberger13], which are K-theory representatives for Schubert varieties. Buch [Reference Buch2, Thm. 3.1] derived the set-valued tableaux generating function for
$G_\lambda $
were introduced in Fomin and Kirillov’s paper [Reference Fomin and Kirillov6] as certain limits of Lascoux and Schützenberger’s Grothendieck polynomials [Reference Lascoux and Schützenberger13], which are K-theory representatives for Schubert varieties. Buch [Reference Buch2, Thm. 3.1] derived the set-valued tableaux generating function for
![]() $G_\lambda $
given in Definition 1.7, and also proved that the stable Grothendieck polynomials are a
$G_\lambda $
given in Definition 1.7, and also proved that the stable Grothendieck polynomials are a
![]() $\mathbb {Z}[\beta ]$
-basis for a ring [Reference Buch2, Cor. 5.5]. For another proof of this ring property, see [Reference Yeliussizov22]. The structure constants
$\mathbb {Z}[\beta ]$
-basis for a ring [Reference Buch2, Cor. 5.5]. For another proof of this ring property, see [Reference Yeliussizov22]. The structure constants
![]() $n_{\lambda \mu }^\nu $
in the expansion
$n_{\lambda \mu }^\nu $
in the expansion
![]() $G_\lambda G_\mu = \sum _{\nu } n_{\lambda \mu }^\nu \beta ^{|\nu | - |\lambda | - |\mu |} G_\nu $
are nonnegative integers with
$G_\lambda G_\mu = \sum _{\nu } n_{\lambda \mu }^\nu \beta ^{|\nu | - |\lambda | - |\mu |} G_\nu $
are nonnegative integers with
![]() $n_{\lambda \mu }^\nu =0$
whenever
$n_{\lambda \mu }^\nu =0$
whenever
![]() $|\nu | < |\lambda | + |\nu |$
or
$|\nu | < |\lambda | + |\nu |$
or
![]() $\ell (\nu )> \ell (\lambda ) + \ell (\mu )$
by [Reference Buch2, Thm. 5.4].
$\ell (\nu )> \ell (\lambda ) + \ell (\mu )$
by [Reference Buch2, Thm. 5.4].
Lam and Pylyavskyy defined
![]() $g_\lambda $
and
$g_\lambda $
and
![]() $j_\lambda $
by the formulas in Theorem 1.10 with
$j_\lambda $
by the formulas in Theorem 1.10 with
![]() $\beta $
set to
$\beta $
set to
![]() $-1$
. They then proved that
$-1$
. They then proved that
![]() $\{ g_\lambda \}$
is the basis for the ring of symmetric functions dual to
$\{ g_\lambda \}$
is the basis for the ring of symmetric functions dual to
![]() $\{G_\lambda \}$
via the Hall inner product [Reference Lam and Pylyavskyy11, Thm. 9.15], along with the identity
$\{G_\lambda \}$
via the Hall inner product [Reference Lam and Pylyavskyy11, Thm. 9.15], along with the identity
![]() $j_\lambda = \omega (g_{\lambda ^\top })$
[Reference Lam and Pylyavskyy11, Prop. 9.25]. For proofs of the Cauchy identity in Definition 1.8 and various generalizations, see [Reference Gunna and Zinn-Justin8, Reference Lascoux and Naruse12, Reference Yeliussizov22].
$j_\lambda = \omega (g_{\lambda ^\top })$
[Reference Lam and Pylyavskyy11, Prop. 9.25]. For proofs of the Cauchy identity in Definition 1.8 and various generalizations, see [Reference Gunna and Zinn-Justin8, Reference Lascoux and Naruse12, Reference Yeliussizov22].
1.7 Outline
We conclude this introduction with a brief outline of the rest of this article. Section 2 contains some miscellaneous results and definitions that are needed in later arguments. The most technical part of our proofs of the main results is showing that the desired generating functions are symmetric. We derive this explicitly for
![]() $j\hspace {-0.1mm}p_\lambda $
and
$j\hspace {-0.1mm}p_\lambda $
and
![]() $j\hspace {-0.1mm}q_\lambda $
by constructing Bender–Knuth involutions for semistandard shifted bar tableaux in Section 3. Once symmetry is established, we are able to prove Theorems 1.4 and 1.5 by an inductive algebraic argument in Section 4.
$j\hspace {-0.1mm}q_\lambda $
by constructing Bender–Knuth involutions for semistandard shifted bar tableaux in Section 3. Once symmetry is established, we are able to prove Theorems 1.4 and 1.5 by an inductive algebraic argument in Section 4.
2 Preliminaries
This section has three parts. Section 2.1 explains the main algebraic consequences of the Cauchy identity (1.1). Section 2.2 gives the precise definitions of the skew forms of the various symmetric functions in the introduction. Section 2.3 derives a Pieri rule for multiplying our dual functions.
2.1 Structure constants
Everywhere below,
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
and
$\mu $
and
![]() $\nu $
are strict partitions. It follows from [Reference Ikeda and Naruse10, Props. 3.4 and 3.5] that there are integers
$\nu $
are strict partitions. It follows from [Reference Ikeda and Naruse10, Props. 3.4 and 3.5] that there are integers
![]() $a_{\lambda \mu }^\nu $
and
$a_{\lambda \mu }^\nu $
and
![]() $b_{\lambda \mu }^\nu $
such that
$b_{\lambda \mu }^\nu $
such that
Let
![]() $\mathbf {y} = (y_1,y_2,\dots )$
be a second set of commuting indeterminates. Given a power series
$\mathbf {y} = (y_1,y_2,\dots )$
be a second set of commuting indeterminates. Given a power series ![]() , let
, let ![]() , and define
, and define
This operation corresponds to the coproduct on the Hopf algebra of symmetric functions; see [Reference Grinberg and Reiner7, §2.1]. It follows from [Reference Lewis and Marberg14, Thms. 4.19 and 5.11] that there are also integers
![]() $\widehat a_{\lambda \mu }^\nu $
and
$\widehat a_{\lambda \mu }^\nu $
and
![]() $\widehat b_{\lambda \mu }^\nu $
such that
$\widehat b_{\lambda \mu }^\nu $
such that
 $$ \begin{align} \begin{aligned} G\hspace{-0.2mm}P_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} \widehat b_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} G\hspace{-0.2mm}P_\lambda(\mathbf{x})G\hspace{-0.2mm}P_\mu(\mathbf{y}), \\ G\hspace{-0.2mm}Q_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} \widehat a_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} G\hspace{-0.2mm}Q_\lambda(\mathbf{x})G\hspace{-0.2mm}Q_\mu(\mathbf{y}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} G\hspace{-0.2mm}P_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} \widehat b_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} G\hspace{-0.2mm}P_\lambda(\mathbf{x})G\hspace{-0.2mm}P_\mu(\mathbf{y}), \\ G\hspace{-0.2mm}Q_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} \widehat a_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} G\hspace{-0.2mm}Q_\lambda(\mathbf{x})G\hspace{-0.2mm}Q_\mu(\mathbf{y}). \end{aligned} \end{align} $$
Observe that the letters a and b here have switched places compared to (2.1). We introduce a third set of integer coefficients
![]() $\widehat c_{\lambda \mu }^\nu $
such that
$\widehat c_{\lambda \mu }^\nu $
such that
The Cauchy identity (1.1) defining
![]() $g\hspace {-0.1mm}p_\lambda $
and
$g\hspace {-0.1mm}p_\lambda $
and
![]() $g\hspace {-0.1mm}q_\lambda $
implies that
$g\hspace {-0.1mm}q_\lambda $
implies that
 $$ \begin{align} \begin{aligned} g\hspace{-0.1mm}p_\lambda g\hspace{-0.1mm}p_\mu &= \sum_\nu \widehat a_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} g\hspace{-0.1mm}p_\nu, \\ g\hspace{-0.1mm}q_\lambda g\hspace{-0.1mm}q_\mu &= \sum_\nu \widehat b_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} g\hspace{-0.1mm}q_\nu, \\ g\hspace{-0.1mm}p_\lambda g\hspace{-0.1mm}q_\mu &= \sum_\nu \widehat c_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} g\hspace{-0.1mm}p_\nu, \\ g\hspace{-0.1mm}p_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} b_{\lambda\mu}^\nu \beta^{|\nu|-|\lambda|-|\mu|} g\hspace{-0.1mm}p_\lambda(\mathbf{x})g\hspace{-0.1mm}p_\mu(\mathbf{y}), \\ g\hspace{-0.1mm}q_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} a_{\lambda\mu}^\nu \beta^{|\nu|-|\lambda|-|\mu|} g\hspace{-0.1mm}q_\lambda(\mathbf{x})g\hspace{-0.1mm}q_\mu(\mathbf{y}). \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} g\hspace{-0.1mm}p_\lambda g\hspace{-0.1mm}p_\mu &= \sum_\nu \widehat a_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} g\hspace{-0.1mm}p_\nu, \\ g\hspace{-0.1mm}q_\lambda g\hspace{-0.1mm}q_\mu &= \sum_\nu \widehat b_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} g\hspace{-0.1mm}q_\nu, \\ g\hspace{-0.1mm}p_\lambda g\hspace{-0.1mm}q_\mu &= \sum_\nu \widehat c_{\lambda\mu}^\nu \beta^{|\lambda|+|\mu|-|\nu|} g\hspace{-0.1mm}p_\nu, \\ g\hspace{-0.1mm}p_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} b_{\lambda\mu}^\nu \beta^{|\nu|-|\lambda|-|\mu|} g\hspace{-0.1mm}p_\lambda(\mathbf{x})g\hspace{-0.1mm}p_\mu(\mathbf{y}), \\ g\hspace{-0.1mm}q_\nu(\mathbf{x}, \mathbf{y}) &= \sum_{\lambda,\mu} a_{\lambda\mu}^\nu \beta^{|\nu|-|\lambda|-|\mu|} g\hspace{-0.1mm}q_\lambda(\mathbf{x})g\hspace{-0.1mm}q_\mu(\mathbf{y}). \end{aligned}\end{align} $$
We explain how to derive the bottom left identity; the others are special cases of [Reference Nakagawa and Naruse19, Prop. 3.2] and follow similarly. Introducing a third sequence of variables
![]() $\mathbf {z} = (z_1,z_2,\dots )$
, one can write
$\mathbf {z} = (z_1,z_2,\dots )$
, one can write
 $$\begin{align*}\begin{aligned}\sum_{\nu} G\hspace{-0.2mm}Q_\nu(\mathbf{x},\mathbf{y}) g\hspace{-0.1mm}p_\nu(\mathbf{z}) &= \prod_{i,j \geq 1} \frac{ 1 - \overline{x_i} z_j}{1-x_iz_j}\cdot \prod_{i,j \geq 1} \frac{ 1 - \overline{y_i} z_j}{1-y_iz_j} \\ &= \left(\sum_{\lambda} G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) g\hspace{-0.1mm}p_\lambda(\mathbf{z})\right) \left( \sum_{\mu} G\hspace{-0.2mm}P_\mu(\mathbf{y}) g\hspace{-0.1mm}q_\mu(\mathbf{z})\right) \\ &= \sum_{\lambda,\mu} G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) G\hspace{-0.2mm}P_\mu(\mathbf{y}) g\hspace{-0.1mm}p_\lambda(\mathbf{z})g\hspace{-0.1mm}q_\mu(\mathbf{z}). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}\sum_{\nu} G\hspace{-0.2mm}Q_\nu(\mathbf{x},\mathbf{y}) g\hspace{-0.1mm}p_\nu(\mathbf{z}) &= \prod_{i,j \geq 1} \frac{ 1 - \overline{x_i} z_j}{1-x_iz_j}\cdot \prod_{i,j \geq 1} \frac{ 1 - \overline{y_i} z_j}{1-y_iz_j} \\ &= \left(\sum_{\lambda} G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) g\hspace{-0.1mm}p_\lambda(\mathbf{z})\right) \left( \sum_{\mu} G\hspace{-0.2mm}P_\mu(\mathbf{y}) g\hspace{-0.1mm}q_\mu(\mathbf{z})\right) \\ &= \sum_{\lambda,\mu} G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) G\hspace{-0.2mm}P_\mu(\mathbf{y}) g\hspace{-0.1mm}p_\lambda(\mathbf{z})g\hspace{-0.1mm}q_\mu(\mathbf{z}). \end{aligned} \end{align*}$$
Then by substituting (2.3) into the first expression and equating coefficients of
![]() $G\hspace {-0.2mm}Q_\lambda (\mathbf {x}) G\hspace {-0.2mm}P_\mu (\mathbf {y})$
, one obtains the identity
$G\hspace {-0.2mm}Q_\lambda (\mathbf {x}) G\hspace {-0.2mm}P_\mu (\mathbf {y})$
, one obtains the identity
![]() $g\hspace {-0.1mm}p_\lambda g\hspace {-0.1mm}q_\mu = \sum _\nu \widehat c_{\lambda \mu }^\nu \beta ^{|\lambda |+|\mu |-|\nu |} g\hspace {-0.1mm}p_\nu $
, as desired.
$g\hspace {-0.1mm}p_\lambda g\hspace {-0.1mm}q_\mu = \sum _\nu \widehat c_{\lambda \mu }^\nu \beta ^{|\lambda |+|\mu |-|\nu |} g\hspace {-0.1mm}p_\nu $
, as desired.
Since
![]() $\omega $
is a bialgebra automorphism, the formulas in (2.4) still hold if we replace every ‘
$\omega $
is a bialgebra automorphism, the formulas in (2.4) still hold if we replace every ‘
![]() $g\hspace {-0.1mm}p$
’ by ‘
$g\hspace {-0.1mm}p$
’ by ‘
![]() $j\hspace {-0.1mm}p$
’ and every ‘
$j\hspace {-0.1mm}p$
’ and every ‘
![]() $g\hspace {-0.1mm}q$
’ by ‘
$g\hspace {-0.1mm}q$
’ by ‘
![]() $j\hspace {-0.1mm}q$
’.
$j\hspace {-0.1mm}q$
’.
The coefficients
![]() $\widehat a_{\lambda \mu }^\nu $
and
$\widehat a_{\lambda \mu }^\nu $
and
![]() $\widehat b_{\lambda \mu }^\nu $
are zero whenever
$\widehat b_{\lambda \mu }^\nu $
are zero whenever
![]() $|\nu |> |\lambda | +|\mu |$
by [Reference Chiu and Marberg4, Eq. (5.6)]; since
$|\nu |> |\lambda | +|\mu |$
by [Reference Chiu and Marberg4, Eq. (5.6)]; since
![]() $g\hspace {-0.1mm}q_\mu $
is a linear combination of
$g\hspace {-0.1mm}q_\mu $
is a linear combination of
![]() $g\hspace {-0.1mm}p_\kappa $
’s with
$g\hspace {-0.1mm}p_\kappa $
’s with
![]() $\kappa \subseteq \mu $
by [Reference Chiu and Marberg4, Cor. 6.2], the same must be true of
$\kappa \subseteq \mu $
by [Reference Chiu and Marberg4, Cor. 6.2], the same must be true of
![]() $ \widehat c_{\lambda \mu }^\nu $
. Thus, the sums on the left side of (2.4) can be limited to strict partitions with
$ \widehat c_{\lambda \mu }^\nu $
. Thus, the sums on the left side of (2.4) can be limited to strict partitions with
![]() $|\nu | \leq |\lambda | +|\mu |$
. Likewise, the coefficients
$|\nu | \leq |\lambda | +|\mu |$
. Likewise, the coefficients
![]() $ a_{\lambda \mu }^\nu $
and
$ a_{\lambda \mu }^\nu $
and
![]() $ b_{\lambda \mu }^\nu $
are zero whenever
$ b_{\lambda \mu }^\nu $
are zero whenever
![]() $|\nu | < |\lambda | +|\mu |$
by [Reference Chiu and Marberg4, Prop. 6.5], so the sums on the right side of (2.4) can be limited to strict partitions with
$|\nu | < |\lambda | +|\mu |$
by [Reference Chiu and Marberg4, Prop. 6.5], so the sums on the right side of (2.4) can be limited to strict partitions with
![]() $|\lambda | +|\mu | \leq |\nu |$
.
$|\lambda | +|\mu | \leq |\nu |$
.
2.2 Skew generalizations
We write
![]() $\mu \subseteq \lambda $
if
$\mu \subseteq \lambda $
if
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
are partitions with
$\lambda $
are partitions with
![]() $\mu _i \leq \lambda _i$
for all i. If
$\mu _i \leq \lambda _i$
for all i. If
![]() $\mu \subseteq \lambda $
are strict partitions, then the shifted diagram of
$\mu \subseteq \lambda $
are strict partitions, then the shifted diagram of
![]() $\lambda /\mu $
is the set difference
$\lambda /\mu $
is the set difference
![]() $\textsf {SD}_{\lambda /\mu } := \textsf {SD}_\lambda - \textsf {SD}_\mu $
. We define shifted set-valued tableaux, plane partitions and bar tableaux of skew shape
$\textsf {SD}_{\lambda /\mu } := \textsf {SD}_\lambda - \textsf {SD}_\mu $
. We define shifted set-valued tableaux, plane partitions and bar tableaux of skew shape
![]() $\lambda /\mu $
in exactly the same way as in the introduction, only now the relevant objects are fillings of
$\lambda /\mu $
in exactly the same way as in the introduction, only now the relevant objects are fillings of
![]() $\textsf {SD}_{\lambda /\mu }$
. The definitions of all related weight statistics like the monomials
$\textsf {SD}_{\lambda /\mu }$
. The definitions of all related weight statistics like the monomials
![]() $\mathbf {x}^T$
are also unchanged. Some relevant notation is as follows:
$\mathbf {x}^T$
are also unchanged. Some relevant notation is as follows:
-
• Let
 $\mathsf {ShSVT}_Q(\lambda /\mu )$
be the set of semistandard shifted set-valued tableaux of shape
$\mathsf {ShSVT}_Q(\lambda /\mu )$
be the set of semistandard shifted set-valued tableaux of shape
 $\lambda /\mu $
, and let
$\lambda /\mu $
, and let
 $\mathsf {ShSVT}_P(\lambda /\mu )$
be the subset of such tableaux with no primed numbers in diagonal boxes.
$\mathsf {ShSVT}_P(\lambda /\mu )$
be the subset of such tableaux with no primed numbers in diagonal boxes. -
• Let
 $\mathsf {ShPP}_Q(\lambda /\mu )$
be the set of shifted plane partitions of shape
$\mathsf {ShPP}_Q(\lambda /\mu )$
be the set of shifted plane partitions of shape
 $\lambda /\mu $
, and let
$\lambda /\mu $
, and let
 $ \mathsf {ShPP}_P(\lambda /\mu )$
be the subset of such fillings with no unprimed diagonal entries.
$ \mathsf {ShPP}_P(\lambda /\mu )$
be the subset of such fillings with no unprimed diagonal entries. -
• Let
 $\mathsf {ShBT}_Q(\lambda /\mu )$
be the set of semistandard shifted bar tableaux of shape
$\mathsf {ShBT}_Q(\lambda /\mu )$
be the set of semistandard shifted bar tableaux of shape
 $\lambda /\mu $
, and let
$\lambda /\mu $
, and let
 $\mathsf {ShBT}_P(\lambda /\mu )$
be the subset of such tableaux with no primed diagonal entries.
$\mathsf {ShBT}_P(\lambda /\mu )$
be the subset of such tableaux with no primed diagonal entries.
We define these sets to be empty if
![]() $\mu \not \subseteq \lambda $
. These sets will index the terms in generating functions for the skew analogues of
$\mu \not \subseteq \lambda $
. These sets will index the terms in generating functions for the skew analogues of
![]() $G\hspace {-0.2mm}Q_\lambda $
,
$G\hspace {-0.2mm}Q_\lambda $
,
![]() $G\hspace {-0.2mm}P_\lambda $
,
$G\hspace {-0.2mm}P_\lambda $
,
![]() $g\hspace {-0.1mm}q_\lambda $
,
$g\hspace {-0.1mm}q_\lambda $
,
![]() $g\hspace {-0.1mm}p_\lambda $
,
$g\hspace {-0.1mm}p_\lambda $
,
![]() $j\hspace {-0.1mm}q_\lambda $
and
$j\hspace {-0.1mm}q_\lambda $
and
![]() $j\hspace {-0.1mm}p_\lambda $
, which are defined as follows:
$j\hspace {-0.1mm}p_\lambda $
, which are defined as follows:
Definition 2.1. For a strict partition
![]() $\lambda $
, let
$\lambda $
, let ![]() be the elements with
be the elements with
where the sums are over all strict partitions
![]() $\mu $
.
$\mu $
.
Both
![]() $g\hspace {-0.1mm}p_{\lambda /\mu }$
and
$g\hspace {-0.1mm}p_{\lambda /\mu }$
and
![]() $g\hspace {-0.1mm}q_{\lambda /\mu }$
are symmetric and homogeneous if
$g\hspace {-0.1mm}q_{\lambda /\mu }$
are symmetric and homogeneous if
![]() $\deg \beta = 1$
, but the families of such functions are no longer linearly independent. These power series are defined when
$\deg \beta = 1$
, but the families of such functions are no longer linearly independent. These power series are defined when
![]() $\mu \not \subseteq \lambda $
, but one can show that
$\mu \not \subseteq \lambda $
, but one can show that
![]() $ g\hspace {-0.1mm}p_{\lambda /\mu }$
and
$ g\hspace {-0.1mm}p_{\lambda /\mu }$
and
![]() $g\hspace {-0.1mm}q_{\lambda /\mu }$
are each nonzero if and only if
$g\hspace {-0.1mm}q_{\lambda /\mu }$
are each nonzero if and only if
![]() $\mu \subseteq \lambda $
[Reference Chiu and Marberg4, Props. 6.5 and 6.7].
$\mu \subseteq \lambda $
[Reference Chiu and Marberg4, Props. 6.5 and 6.7].
Definition 2.2. For a strict partition
![]() $\lambda $
, let
$\lambda $
, let ![]() be the elements with
be the elements with
where the sums are over all strict partitions
![]() $\mu $
.
$\mu $
.
Equivalently, one could define these skew analogues by the following formula:
Proposition 2.3 [Reference Chiu and Marberg4, Eq. (7.4)].
It holds that
![]() $j\hspace {-0.1mm}p_{\lambda /\mu } = \omega (g\hspace {-0.1mm}p_{\lambda /\mu })$
and
$j\hspace {-0.1mm}p_{\lambda /\mu } = \omega (g\hspace {-0.1mm}p_{\lambda /\mu })$
and
![]() $ j\hspace {-0.1mm}q_{\lambda /\mu } = \omega (g\hspace {-0.1mm}q_{\lambda /\mu }).$
$ j\hspace {-0.1mm}q_{\lambda /\mu } = \omega (g\hspace {-0.1mm}q_{\lambda /\mu }).$
The skew versions of
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
that are most relevant to our discussion are not the obvious generating functions for the sets
$G\hspace {-0.2mm}Q_\lambda $
that are most relevant to our discussion are not the obvious generating functions for the sets
![]() $\mathsf {ShSVT}_P(\lambda /\mu )$
and
$\mathsf {ShSVT}_P(\lambda /\mu )$
and
![]() $\mathsf {ShSVT}_Q(\lambda /\mu )$
. Instead, define a removable corner box of
$\mathsf {ShSVT}_Q(\lambda /\mu )$
. Instead, define a removable corner box of
![]() $\textsf {SD}_\lambda $
to be a position
$\textsf {SD}_\lambda $
to be a position
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $\textsf {SD}_\lambda - \{(i,j)\} = \textsf {SD}_\mu $
for a strict partition
$\textsf {SD}_\lambda - \{(i,j)\} = \textsf {SD}_\mu $
for a strict partition
![]() $\mu \neq \lambda $
. Let
$\mu \neq \lambda $
. Let
![]() $\mathsf {RC}(\lambda )$
denote the set of such boxes in
$\mathsf {RC}(\lambda )$
denote the set of such boxes in
![]() $\textsf {SD}_\lambda $
. For strict partitions
$\textsf {SD}_\lambda $
. For strict partitions
![]() $\mu \subseteq \lambda $
, define
$\mu \subseteq \lambda $
, define
 $$\begin{align*}\mathsf{ShSVT}_P(\lambda/\hspace{-1mm}/\mu) := \bigsqcup_{\substack{\nu \subseteq\mu \\ \textsf{SD}_{\mu/\nu}\subseteq \mathsf{RC}(\mu)}} \mathsf{ShSVT}_P(\lambda/\nu) \end{align*}$$
$$\begin{align*}\mathsf{ShSVT}_P(\lambda/\hspace{-1mm}/\mu) := \bigsqcup_{\substack{\nu \subseteq\mu \\ \textsf{SD}_{\mu/\nu}\subseteq \mathsf{RC}(\mu)}} \mathsf{ShSVT}_P(\lambda/\nu) \end{align*}$$
and
 $$\begin{align*}\mathsf{ShSVT}_Q(\lambda/\hspace{-1mm}/\mu) := \bigsqcup_{\substack{\nu \subseteq\mu \\ \textsf{SD}_{\mu/\nu}\subseteq \mathsf{RC}(\mu)}} \mathsf{ShSVT}_Q(\lambda/\nu), \end{align*}$$
$$\begin{align*}\mathsf{ShSVT}_Q(\lambda/\hspace{-1mm}/\mu) := \bigsqcup_{\substack{\nu \subseteq\mu \\ \textsf{SD}_{\mu/\nu}\subseteq \mathsf{RC}(\mu)}} \mathsf{ShSVT}_Q(\lambda/\nu), \end{align*}$$
where the unions are over all strict partitions
![]() $\nu $
such that
$\nu $
such that
![]() $\nu \subseteq \mu $
and
$\nu \subseteq \mu $
and
![]() $\textsf {SD}_{\mu /\nu }\subseteq \mathsf {RC}(\mu )$
. For strict partitions
$\textsf {SD}_{\mu /\nu }\subseteq \mathsf {RC}(\mu )$
. For strict partitions
![]() $\mu \not \subseteq \lambda $
, set
$\mu \not \subseteq \lambda $
, set
![]() $\mathsf {ShSVT}_P(\lambda /\hspace {-1mm}/\mu )=\mathsf {ShSVT}_Q(\lambda /\hspace {-1mm}/\mu ):= \varnothing $
.
$\mathsf {ShSVT}_P(\lambda /\hspace {-1mm}/\mu )=\mathsf {ShSVT}_Q(\lambda /\hspace {-1mm}/\mu ):= \varnothing $
.
Definition 2.4. For strict partitions
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
, define
$\lambda $
, define
![]() $|\lambda /\mu | := |\lambda |-|\mu |$
and let
$|\lambda /\mu | := |\lambda |-|\mu |$
and let
 $$\begin{align*}\begin{aligned} G\hspace{-0.2mm}P_{\lambda/\hspace{-1mm}/\mu} := \sum_{T \in \mathsf{ShSVT}_P(\lambda/\hspace{-1mm}/\mu)} \beta^{|\lambda/\mu|-|T|} \mathbf{x}^{T}\quad\text{and}\quad G\hspace{-0.2mm}Q_{\lambda/\hspace{-1mm}/\mu} := \sum_{T \in \mathsf{ShSVT}_Q(\lambda/\hspace{-1mm}/\mu)} \beta^{|\lambda/\mu|-|T|} \mathbf{x}^{T}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} G\hspace{-0.2mm}P_{\lambda/\hspace{-1mm}/\mu} := \sum_{T \in \mathsf{ShSVT}_P(\lambda/\hspace{-1mm}/\mu)} \beta^{|\lambda/\mu|-|T|} \mathbf{x}^{T}\quad\text{and}\quad G\hspace{-0.2mm}Q_{\lambda/\hspace{-1mm}/\mu} := \sum_{T \in \mathsf{ShSVT}_Q(\lambda/\hspace{-1mm}/\mu)} \beta^{|\lambda/\mu|-|T|} \mathbf{x}^{T}. \end{aligned}\end{align*}$$
Observe that while
![]() $G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/ \emptyset } =G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/ \emptyset } =G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\emptyset } = G\hspace {-0.2mm}Q_\lambda $
, the functions
$G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\emptyset } = G\hspace {-0.2mm}Q_\lambda $
, the functions
![]() $G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/ \lambda }$
and
$G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/ \lambda }$
and
![]() $G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/ \lambda }$
are typically not equal to
$G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/ \lambda }$
are typically not equal to
![]() $1$
. Both
$1$
. Both
![]() $G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/\mu } $
and
$G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/\mu } $
and
![]() $G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\mu } $
are zero if
$G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\mu } $
are zero if
![]() $\mu \not \subseteq \lambda $
since the sets indexing the relevant summations are both empty. These power series are symmetric since we have
$\mu \not \subseteq \lambda $
since the sets indexing the relevant summations are both empty. These power series are symmetric since we have
and the power series
![]() $G\hspace {-0.2mm}P_\lambda $
and
$G\hspace {-0.2mm}P_\lambda $
and
![]() $G\hspace {-0.2mm}Q_\lambda $
are symmetric.
$G\hspace {-0.2mm}Q_\lambda $
are symmetric.
There are several more general versions of the Cauchy identity (1.1) that relate all of these families of skew functions; see [Reference Chiu and Marberg4, Thm. 6.9 and Cor. 7.8]. Two such identities needed later are given as follows. Let
![]() $\mu $
and
$\mu $
and
![]() $\nu $
be strict partitions. Then by [Reference Chiu and Marberg4, Cor. 7.8], we have
$\nu $
be strict partitions. Then by [Reference Chiu and Marberg4, Cor. 7.8], we have
 $$ \begin{align} \sum_\lambda G\hspace{-0.2mm}P_{\lambda/\hspace{-1mm}/\mu}(\mathbf{x}) j\hspace{-0.1mm}q_{\lambda/\nu}(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{1 + x_iy_j}{ 1 + \overline{x_i} y_j} \sum_\kappa G\hspace{-0.2mm}P_{\nu/\hspace{-1mm}/\kappa}(\mathbf{x}) j\hspace{-0.1mm}q_{\mu/\kappa}(\mathbf{y}) \end{align} $$
$$ \begin{align} \sum_\lambda G\hspace{-0.2mm}P_{\lambda/\hspace{-1mm}/\mu}(\mathbf{x}) j\hspace{-0.1mm}q_{\lambda/\nu}(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{1 + x_iy_j}{ 1 + \overline{x_i} y_j} \sum_\kappa G\hspace{-0.2mm}P_{\nu/\hspace{-1mm}/\kappa}(\mathbf{x}) j\hspace{-0.1mm}q_{\mu/\kappa}(\mathbf{y}) \end{align} $$
and
 $$ \begin{align} \sum_\lambda G\hspace{-0.2mm}Q_{\lambda/\hspace{-1mm}/\mu}(\mathbf{x}) j\hspace{-0.1mm}p_{\lambda/\nu}(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{1 + x_iy_j}{ 1 + \overline{x_i} y_j} \sum_\kappa G\hspace{-0.2mm}Q_{\nu/\hspace{-1mm}/\kappa}(\mathbf{x}) j\hspace{-0.1mm}p_{\mu/\kappa}(\mathbf{y}), \end{align} $$
$$ \begin{align} \sum_\lambda G\hspace{-0.2mm}Q_{\lambda/\hspace{-1mm}/\mu}(\mathbf{x}) j\hspace{-0.1mm}p_{\lambda/\nu}(\mathbf{y}) = \prod_{i,j \geq 1} \tfrac{1 + x_iy_j}{ 1 + \overline{x_i} y_j} \sum_\kappa G\hspace{-0.2mm}Q_{\nu/\hspace{-1mm}/\kappa}(\mathbf{x}) j\hspace{-0.1mm}p_{\mu/\kappa}(\mathbf{y}), \end{align} $$
where
![]() $\overline {x} := \frac {-x}{1+\beta x}$
as in Section 1.2 and the sums are over all strict partitions
$\overline {x} := \frac {-x}{1+\beta x}$
as in Section 1.2 and the sums are over all strict partitions
![]() $\lambda $
and
$\lambda $
and
![]() $\kappa $
.
$\kappa $
.
2.3 Pieri rules
Buch and Ravikumar derived Pieri rules in [Reference Buch and Ravikumar3] to compute
![]() $a_{\lambda \mu }^\nu $
and
$a_{\lambda \mu }^\nu $
and
![]() $b_{\lambda \mu }^\nu $
when
$b_{\lambda \mu }^\nu $
when
![]() $\mu = (n)$
is a one-row partition. Here, we describe analogous formulas for
$\mu = (n)$
is a one-row partition. Here, we describe analogous formulas for
![]() $\widehat a_{\lambda \mu }^\nu $
,
$\widehat a_{\lambda \mu }^\nu $
,
![]() $\widehat b_{\lambda \mu }^\nu $
, and
$\widehat b_{\lambda \mu }^\nu $
, and
![]() $\widehat c_{\lambda \mu }^\nu $
when
$\widehat c_{\lambda \mu }^\nu $
when
![]() $\mu =(n)$
.
$\mu =(n)$
.
We define a shifted ribbon to be a shifted skew shape
![]() $\textsf {SD}_{\nu /\lambda }$
that does not contain two boxes
$\textsf {SD}_{\nu /\lambda }$
that does not contain two boxes
![]() $(i_1,j_1)$
and
$(i_1,j_1)$
and
![]() $(i_2,j_2)$
with
$(i_2,j_2)$
with
![]() $i_1<i_2$
and
$i_1<i_2$
and
![]() $j_1<j_2$
. We do not require this shape to be connected, so
$j_1<j_2$
. We do not require this shape to be connected, so

are both shifted ribbons. In general, if
![]() $\nu = (\nu _1> \nu _2 > \nu _3 > \dots > \nu _k > 0)$
, then
$\nu = (\nu _1> \nu _2 > \nu _3 > \dots > \nu _k > 0)$
, then
![]() $\textsf {SD}_{\nu /\lambda }$
is a shifted ribbon if and only if the partition
$\textsf {SD}_{\nu /\lambda }$
is a shifted ribbon if and only if the partition
![]() $ (\nu _2, \nu _3,\dots , \nu _k) $
is contained in
$ (\nu _2, \nu _3,\dots , \nu _k) $
is contained in
![]() $ \lambda $
.
$ \lambda $
.
The row reading word order of
![]() $\mathbb {Z} \times \mathbb {Z}$
has
$\mathbb {Z} \times \mathbb {Z}$
has
![]() $(i_1,j_1) < (i_2,j_2)$
if
$(i_1,j_1) < (i_2,j_2)$
if
![]() $i_1> i_2$
or if
$i_1> i_2$
or if
![]() $i_1=i_2$
and
$i_1=i_2$
and
![]() $j_1<j_2$
. Suppose T is a semistandard set-valued shifted tableau containing only
$j_1<j_2$
. Suppose T is a semistandard set-valued shifted tableau containing only
![]() $1'$
and
$1'$
and
![]() $1$
. Then the shape of T must be a shifted ribbon, and any entry which is not the first in its connected component (in row reading order) is uniquely determined and given by the sets
$1$
. Then the shape of T must be a shifted ribbon, and any entry which is not the first in its connected component (in row reading order) is uniquely determined and given by the sets
![]() $\{1'\}$
or
$\{1'\}$
or
![]() $\{1\}$
. However, the first entries in each connected component of T may be any of
$\{1\}$
. However, the first entries in each connected component of T may be any of
![]() $\{1'\}$
,
$\{1'\}$
,
![]() $\{1\}$
, or
$\{1\}$
, or
![]() $\{1',1\}$
.
$\{1',1\}$
.
Example 2.5. Two such tableaux of shape
![]() $(8,5,3,1)/(5,4,1)$
are given by
$(8,5,3,1)/(5,4,1)$
are given by

There are seven other such tableaux of this shape.
For strict partitions
![]() $\lambda \subseteq \nu $
, define
$\lambda \subseteq \nu $
, define
![]() $\mathsf {ShRibbons}_Q(\nu /\lambda )$
to be the set of semistandard shifted set-valued tableaux of shape
$\mathsf {ShRibbons}_Q(\nu /\lambda )$
to be the set of semistandard shifted set-valued tableaux of shape
![]() $\textsf {SD}_{\nu /\lambda }$
containing only
$\textsf {SD}_{\nu /\lambda }$
containing only
![]() $1'$
and
$1'$
and
![]() $1$
as entries. Then let
$1$
as entries. Then let
 $$\begin{align*}\mathsf{ShRibbons}_Q(\nu/\hspace{-1mm}/\lambda) := \bigsqcup_{\substack{\mu \subseteq \lambda \\ \textsf{SD}_{\lambda/\mu} \subseteq \mathsf{RC}(\lambda)}} \mathsf{ShRibbons}_Q(\nu/\mu),\end{align*}$$
$$\begin{align*}\mathsf{ShRibbons}_Q(\nu/\hspace{-1mm}/\lambda) := \bigsqcup_{\substack{\mu \subseteq \lambda \\ \textsf{SD}_{\lambda/\mu} \subseteq \mathsf{RC}(\lambda)}} \mathsf{ShRibbons}_Q(\nu/\mu),\end{align*}$$
where the union is over strict partitions
![]() $\mu $
whose shifted diagrams are formed by deleting a possibly empty set of removable corner boxes from
$\mu $
whose shifted diagrams are formed by deleting a possibly empty set of removable corner boxes from
![]() $\textsf {SD}_\lambda $
. The set
$\textsf {SD}_\lambda $
. The set
![]() $\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda ) $
is nonempty if and only if
$\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda ) $
is nonempty if and only if
![]() $\textsf {SD}_{\nu /\lambda }$
is a shifted ribbon, and we have
$\textsf {SD}_{\nu /\lambda }$
is a shifted ribbon, and we have
![]() $|\mathsf {ShRibbons}_Q(\nu /\nu )|=1\leq |\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\nu )|=4^{|\mathsf {RC}(\nu )|}$
.
$|\mathsf {ShRibbons}_Q(\nu /\nu )|=1\leq |\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\nu )|=4^{|\mathsf {RC}(\nu )|}$
.
Example 2.6. If
![]() $\lambda =(5,4,1)\subseteq \nu =(8,5,3,1)$
, then
$\lambda =(5,4,1)\subseteq \nu =(8,5,3,1)$
, then
![]() $\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda )$
consists of
$\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda )$
consists of

in addition to the nine elements of
![]() $\mathsf {ShRibbons}_Q(\nu /\lambda )$
.
$\mathsf {ShRibbons}_Q(\nu /\lambda )$
.
Let
![]() $\mathsf {ShRibbons}_P(\nu /\hspace {-1mm}/\lambda )$
be the set of elements in
$\mathsf {ShRibbons}_P(\nu /\hspace {-1mm}/\lambda )$
be the set of elements in
![]() $\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda )$
with no primed numbers appearing in any diagonal boxes. Set
$\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda )$
with no primed numbers appearing in any diagonal boxes. Set
for strict partitions
![]() $\lambda \not \subseteq \nu $
. For integers
$\lambda \not \subseteq \nu $
. For integers
![]() $n \geq 0$
, define
$n \geq 0$
, define
to be the subsets of tableaux T with
![]() $\mathbf {x}^T = x_1^n$
.
$\mathbf {x}^T = x_1^n$
.
Proposition 2.7. Suppose
![]() $\lambda $
and
$\lambda $
and
![]() $\nu $
are strict partitions and
$\nu $
are strict partitions and
![]() $n\in \mathbb {Z}_{\geq 0}$
. Then
$n\in \mathbb {Z}_{\geq 0}$
. Then
Proof. For simplicity, assume
![]() $\beta =1$
. Then
$\beta =1$
. Then
![]() $ \widehat c_{\lambda ,(n)}^\nu $
is the coefficient of
$ \widehat c_{\lambda ,(n)}^\nu $
is the coefficient of
![]() $G\hspace {-0.2mm}Q_{\lambda }(\mathbf {x})G\hspace {-0.2mm}P_{(n)}(\mathbf {y})$
in
$G\hspace {-0.2mm}Q_{\lambda }(\mathbf {x})G\hspace {-0.2mm}P_{(n)}(\mathbf {y})$
in
![]() $G\hspace {-0.2mm}Q_\nu (\mathbf {x}, \mathbf {y})$
. Since
$G\hspace {-0.2mm}Q_\nu (\mathbf {x}, \mathbf {y})$
. Since
![]() $G\hspace {-0.2mm}P_\mu (y_1,0,0,\dots )$
is zero if
$G\hspace {-0.2mm}P_\mu (y_1,0,0,\dots )$
is zero if
![]() $\ell (\mu ) \geq 2$
and equal to
$\ell (\mu ) \geq 2$
and equal to
![]() $y_1^{\mu _1}$
if
$y_1^{\mu _1}$
if
![]() $\ell (\mu ) \leq 1$
, the number
$\ell (\mu ) \leq 1$
, the number
![]() $ \widehat c_{\lambda ,(n)}^\nu $
is also the coefficient of
$ \widehat c_{\lambda ,(n)}^\nu $
is also the coefficient of
![]() $G\hspace {-0.2mm}Q_{\lambda }(\mathbf {x}) t^n$
in the power series
$G\hspace {-0.2mm}Q_{\lambda }(\mathbf {x}) t^n$
in the power series
![]() $G\hspace {-0.2mm}Q_\nu (\mathbf {x};t) $
formed by setting
$G\hspace {-0.2mm}Q_\nu (\mathbf {x};t) $
formed by setting
![]() $y_1= t$
and
$y_1= t$
and
![]() $y_2=y_3=\dots =0$
in
$y_2=y_3=\dots =0$
in
![]() $G\hspace {-0.2mm}Q_\nu (\mathbf {x}, \mathbf {y})$
. As
$G\hspace {-0.2mm}Q_\nu (\mathbf {x}, \mathbf {y})$
. As
![]() $G\hspace {-0.2mm}Q_\nu = \sum _{T \in \mathsf {ShSVT}_Q(\nu )} \mathbf {x}^{T}$
is symmetric, it holds that
$G\hspace {-0.2mm}Q_\nu = \sum _{T \in \mathsf {ShSVT}_Q(\nu )} \mathbf {x}^{T}$
is symmetric, it holds that
and so we have
![]() $ \widehat c_{\lambda ,(n)}^\nu =|\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda; n)|.$
The argument to show that we likewise have
$ \widehat c_{\lambda ,(n)}^\nu =|\mathsf {ShRibbons}_Q(\nu /\hspace {-1mm}/\lambda; n)|.$
The argument to show that we likewise have
![]() $\widehat b_{\lambda ,(n)}^\nu =|\mathsf {ShRibbons}_P(\nu /\hspace {-1mm}/\lambda; n)|$
is similar, as
$\widehat b_{\lambda ,(n)}^\nu =|\mathsf {ShRibbons}_P(\nu /\hspace {-1mm}/\lambda; n)|$
is similar, as
![]() $\widehat b_{\lambda ,(n)}^\nu $
is the coefficient of
$\widehat b_{\lambda ,(n)}^\nu $
is the coefficient of
![]() $G\hspace {-0.2mm}P_{\lambda }(\mathbf {x}) t^n$
in
$G\hspace {-0.2mm}P_{\lambda }(\mathbf {x}) t^n$
in
![]() $G\hspace {-0.2mm}P_\nu (\mathbf {x};t) $
.
$G\hspace {-0.2mm}P_\nu (\mathbf {x};t) $
.
It is slightly less straightforward to interpret the numbers
![]() $\widehat a_{\lambda ,(n)}^\nu $
along these lines. However, if
$\widehat a_{\lambda ,(n)}^\nu $
along these lines. However, if
![]() $n>0$
, then it is easy to check that
$n>0$
, then it is easy to check that
![]() $g\hspace {-0.1mm}q_n = 2g\hspace {-0.1mm}p_n + [n>1] \beta g\hspace {-0.1mm}p_{n-1}$
, and so (2.4) implies that
$g\hspace {-0.1mm}q_n = 2g\hspace {-0.1mm}p_n + [n>1] \beta g\hspace {-0.1mm}p_{n-1}$
, and so (2.4) implies that
3 Bender–Knuth involutions for shifted bar tableaux
In this section, we consider several families of shifted bar tableaux. Recall that these objects are shifted tableaux whose boxes are divided into bars, each consisting of a contiguous sequence of equal primed entries in one column or equal unprimed entries in one row. In such tableaux, no primed entry can be repeated in a row and no unprimed entry can be repeated in a column.
For this section only, we assume the entries of all shifted bar tableaux are limited to the set
![]() $\mathbf {\{1', 1, 2', 2\}}$
. In this context, the weight of a shifted bar tableau is the pair
$\mathbf {\{1', 1, 2', 2\}}$
. In this context, the weight of a shifted bar tableau is the pair
![]() $(a_1,a_2)$
, where
$(a_1,a_2)$
, where
![]() $a_i$
is the number of bars containing i or
$a_i$
is the number of bars containing i or
![]() $i'$
. Our goal is to construct a shape-preserving and weight-reversing involution of the set of such tableaux that are semistandard, analogous to the Bender–Knuth involutions on usual semistandard Young tableaux.
$i'$
. Our goal is to construct a shape-preserving and weight-reversing involution of the set of such tableaux that are semistandard, analogous to the Bender–Knuth involutions on usual semistandard Young tableaux.
3.1 Sorted bar tableaux
For convenience, we will often abbreviate ‘shifted bar tableau’ as ‘ShBT’. Recall that a ShBT is semistandard if the entries in the tableau (ignoring bars) are weakly increasing in the order
![]() $1'<1<2'<2$
along rows and columns. We will need a variant of this property:
$1'<1<2'<2$
along rows and columns. We will need a variant of this property:
Definition 3.1. Let T be a shifted bar tableau with all entries in
![]() $\{1', 1, 2', 2\}$
. We say that T is sorted if (in addition to our blanket assumption that no primed entry is repeated in any row and no unprimed entry is repeated in any column) any of the following holds:
$\{1', 1, 2', 2\}$
. We say that T is sorted if (in addition to our blanket assumption that no primed entry is repeated in any row and no unprimed entry is repeated in any column) any of the following holds:
-
(a) The entries of T are weakly increasing along rows and columns in the order
 $1' \prec 2' \prec 1\prec 2$
.
$1' \prec 2' \prec 1\prec 2$
. -
(b) T has exactly two diagonal boxes,
 $(i,i)$
and
$(i,i)$
and
 $(i+1,i+1)$
, such that
$(i+1,i+1)$
, such that
 $T_{i,i+1} = 1$
,
$T_{i,i+1} = 1$
,
 $T_{i+1,i+1}=2'$
, and either
$T_{i+1,i+1}=2'$
, and either
 $T_{i,i} = 2'$
or boxes
$T_{i,i} = 2'$
or boxes
 $(i,i)$
and
$(i,i)$
and
 $(i,i+1)$
are part of the same bar with entry
$(i,i+1)$
are part of the same bar with entry
 $1$
, and changing the value in box
$1$
, and changing the value in box
 $(i+1,i+1)$
to
$(i+1,i+1)$
to
 $2$
results in a shifted bar tableau satisfying (a). For example, all of the following are sorted: (3.1)
$2$
results in a shifted bar tableau satisfying (a). For example, all of the following are sorted: (3.1)
-
(c) T has exactly two diagonal boxes
 $(i,i)$
and
$(i,i)$
and
 $(i+1,i+1)$
such that
$(i+1,i+1)$
such that
 $T_{i,i} = 1$
,
$T_{i,i} = 1$
,
 $T_{i,i+1}=2'$
, and either
$T_{i,i+1}=2'$
, and either
 $T_{i+1,i+1} = 1$
or boxes
$T_{i+1,i+1} = 1$
or boxes
 $(i+1,i+1)$
and
$(i+1,i+1)$
and
 $(i,i+1)$
are part of the same bar with entry
$(i,i+1)$
are part of the same bar with entry
 $2'$
, and changing the value in box
$2'$
, and changing the value in box
 $(i,i)$
to
$(i,i)$
to
 $1'$
results in a shifted bar tableau satisfying (a). For example, all of the following are sorted: (3.2)
$1'$
results in a shifted bar tableau satisfying (a). For example, all of the following are sorted: (3.2)
3.2 Ascending swaps
The first (respectively, last) box in a bar within a ShBT is the box
![]() $(i,j)$
with i and j both minimal (respectively, maximal). Everywhere in this subsection, T denotes an arbitrary ShBT with all entries in
$(i,j)$
with i and j both minimal (respectively, maximal). Everywhere in this subsection, T denotes an arbitrary ShBT with all entries in
![]() $\{1' , 2' , 1 , 2\}$
, which is not necessarily semistandard or sorted.
$\{1' , 2' , 1 , 2\}$
, which is not necessarily semistandard or sorted.
Definition 3.2. Suppose
![]() ${\mathcal {H}}$
and
${\mathcal {H}}$
and
![]() ${\mathcal {V}}$
are bars in T with unique entries
${\mathcal {V}}$
are bars in T with unique entries
![]() $1$
and
$1$
and
![]() $2'$
, respectively. Below, we define two new bars
$2'$
, respectively. Below, we define two new bars
![]() $\tilde {\mathcal {H}}$
and
$\tilde {\mathcal {H}}$
and
![]() $\tilde {{\mathcal {V}}}$
whose union
$\tilde {{\mathcal {V}}}$
whose union
![]() $\tilde {\mathcal {H}}\sqcup \tilde {{\mathcal {V}}}$
occupies the same boxes as
$\tilde {\mathcal {H}}\sqcup \tilde {{\mathcal {V}}}$
occupies the same boxes as
![]() ${\mathcal {H}}\sqcup {{\mathcal {V}}}$
. We then set
${\mathcal {H}}\sqcup {{\mathcal {V}}}$
. We then set
where
![]() $\tilde {T}$
is formed from T by replacing
$\tilde {T}$
is formed from T by replacing
![]() ${\mathcal {H}}$
with
${\mathcal {H}}$
with
![]() $\tilde {\mathcal {H}}$
and
$\tilde {\mathcal {H}}$
and
![]() ${\mathcal {V}}$
with
${\mathcal {V}}$
with
![]() $\tilde {{\mathcal {V}}}$
. The rules defining
$\tilde {{\mathcal {V}}}$
. The rules defining
![]() $\tilde {\mathcal {H}}$
and
$\tilde {\mathcal {H}}$
and
![]() $\tilde {\mathcal {V}}$
are as follows:
$\tilde {\mathcal {V}}$
are as follows:
-
(a) Suppose the first boxes of
 ${\mathcal {H}}$
and
${\mathcal {H}}$
and
 ${\mathcal {V}}$
are
${\mathcal {V}}$
are
 $(i,j)$
and
$(i,j)$
and
 $(i+1,j)$
, respectively, and that if
$(i+1,j)$
, respectively, and that if
 $(i,j-1) \in T$
, then
$(i,j-1) \in T$
, then
 $T_{i,j-1}\neq 2'$
. This means boxes
$T_{i,j-1}\neq 2'$
. This means boxes
 $(i,j-1)$
,
$(i,j-1)$
,
 $(i,j)$
,
$(i,j)$
,
 $(i+1,j)$
in T cannot have the form (3.3)since in the first case.
$(i+1,j)$
in T cannot have the form (3.3)since in the first case.
 $T_{i,j-1} = 2'$
, and in the second case, the first boxes of
$T_{i,j-1} = 2'$
, and in the second case, the first boxes of
 ${\mathcal {H}}$
and
${\mathcal {H}}$
and
 ${\mathcal {V}}$
are not in the same column. If
${\mathcal {V}}$
are not in the same column. If
 ${\mathcal {H}}$
has more than one box, then we form
${\mathcal {H}}$
has more than one box, then we form
 $\tilde {\mathcal {H}}$
from
$\tilde {\mathcal {H}}$
from
 ${\mathcal {H}}$
by removing its first box and we form
${\mathcal {H}}$
by removing its first box and we form
 $\tilde {\mathcal {V}}$
by adding this box to
$\tilde {\mathcal {V}}$
by adding this box to
 ${\mathcal {V}}$
. If
${\mathcal {V}}$
. If
 ${\mathcal {H}}$
has only one box, then we form
${\mathcal {H}}$
has only one box, then we form
 $\tilde {\mathcal {V}}$
by moving
$\tilde {\mathcal {V}}$
by moving
 ${\mathcal {V}}$
down one row and we form
${\mathcal {V}}$
down one row and we form
 $\tilde {\mathcal {H}}$
by moving
$\tilde {\mathcal {H}}$
by moving
 ${\mathcal {H}}$
to occupy the last box of
${\mathcal {H}}$
to occupy the last box of
 ${\mathcal {V}}$
. In pictures, we have
${\mathcal {V}}$
. In pictures, we have

where the blue boxes are
 ${\mathcal {H}}$
and
${\mathcal {H}}$
and
 $\tilde {\mathcal {H}}$
and the red boxes are
$\tilde {\mathcal {H}}$
and the red boxes are
 ${\mathcal {V}}$
and
${\mathcal {V}}$
and
 $\tilde {\mathcal {V}}$
.
$\tilde {\mathcal {V}}$
. -
(b) Suppose the last boxes of
 ${\mathcal {H}}$
and
${\mathcal {H}}$
and
 ${\mathcal {V}}$
are
${\mathcal {V}}$
are
 $(i,j)$
and
$(i,j)$
and
 $(i,j+1)$
, respectively, and that if
$(i,j+1)$
, respectively, and that if
 $(i + 1 ,j+1) \in T$
, then
$(i + 1 ,j+1) \in T$
, then
 $T_{i+1,j+1}\neq 1$
. This mean boxes
$T_{i+1,j+1}\neq 1$
. This mean boxes
 $(i,j)$
,
$(i,j)$
,
 $(i,j+1)$
,
$(i,j+1)$
,
 $(i+1,j+1)$
in T cannot have the form (3.4)If
$(i+1,j+1)$
in T cannot have the form (3.4)If
 ${\mathcal {V}}$
has more than one box, then we form
${\mathcal {V}}$
has more than one box, then we form
 $\tilde {\mathcal {V}}$
from
$\tilde {\mathcal {V}}$
from
 ${\mathcal {V}}$
by removing its last box and we form
${\mathcal {V}}$
by removing its last box and we form
 $\tilde {\mathcal {H}}$
by adding this box to
$\tilde {\mathcal {H}}$
by adding this box to
 ${\mathcal {H}}$
. If
${\mathcal {H}}$
. If
 ${\mathcal {V}}$
has only one box, then we form
${\mathcal {V}}$
has only one box, then we form
 $\tilde {\mathcal {H}}$
by moving
$\tilde {\mathcal {H}}$
by moving
 ${\mathcal {H}}$
right one column and we form
${\mathcal {H}}$
right one column and we form
 $\tilde {\mathcal {V}}$
by moving
$\tilde {\mathcal {V}}$
by moving
 ${\mathcal {V}}$
to occupy the first box of
${\mathcal {V}}$
to occupy the first box of
 ${\mathcal {H}}$
. In pictures, we have
${\mathcal {H}}$
. In pictures, we have

-
(c) In all other cases, we set
 $\tilde {\mathcal {H}} := {\mathcal {H}}$
and
$\tilde {\mathcal {H}} := {\mathcal {H}}$
and
 $\tilde {\mathcal {V}} :={\mathcal {V}}$
.
$\tilde {\mathcal {V}} :={\mathcal {V}}$
.
Above, we defined how to ‘swap’ one
![]() $2'$
-bar in T with a
$2'$
-bar in T with a
![]() $1$
-bar. We will extend this to a procedure successively swapping a given
$1$
-bar. We will extend this to a procedure successively swapping a given
![]() $2'$
-bar with all
$2'$
-bar with all
![]() $1$
-bars in a certain order. Then we will further extend that operation to one successively swapping all
$1$
-bars in a certain order. Then we will further extend that operation to one successively swapping all
![]() $2'$
-bars in T with all
$2'$
-bars in T with all
![]() $1$
-bars. This will give an operation transforming T to another ShBT in which the relative order of
$1$
-bars. This will give an operation transforming T to another ShBT in which the relative order of
![]() $1'$
and
$1'$
and
![]() $2$
is reversed.
$2$
is reversed.
Definition 3.3. Suppose
![]() ${\mathcal {H}}_1,{\mathcal {H}}_2,\dots ,{\mathcal {H}}_k$
are the distinct bars of T containing
${\mathcal {H}}_1,{\mathcal {H}}_2,\dots ,{\mathcal {H}}_k$
are the distinct bars of T containing
![]() $1$
ordered from right to left, so if
$1$
ordered from right to left, so if
![]() $i < j$
, then
$i < j$
, then
![]() ${\mathcal {H}}_i$
occurs in larger-indexed columns than
${\mathcal {H}}_i$
occurs in larger-indexed columns than
![]() ${\mathcal {H}}_j$
. For any single bar
${\mathcal {H}}_j$
. For any single bar
![]() $ {\mathcal {V}}$
of T with unique entry
$ {\mathcal {V}}$
of T with unique entry
![]() $2'$
, inductively define
$2'$
, inductively define
 $$\begin{align*}\begin{aligned} (\tilde T_0, \tilde {\mathcal{V}}_0) &:= (T,{\mathcal{V}}), \\ (\tilde T_{i},\tilde{\mathcal{V}}_{i}) &:= \mathsf{swap}_{1\leftrightarrow 2'}(\tilde T_{i-1},\tilde{\mathcal{V}}_{i-1}, {\mathcal{H}}_i)\text{ for} i=1,2,\dots,k,\end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} (\tilde T_0, \tilde {\mathcal{V}}_0) &:= (T,{\mathcal{V}}), \\ (\tilde T_{i},\tilde{\mathcal{V}}_{i}) &:= \mathsf{swap}_{1\leftrightarrow 2'}(\tilde T_{i-1},\tilde{\mathcal{V}}_{i-1}, {\mathcal{H}}_i)\text{ for} i=1,2,\dots,k,\end{aligned}\end{align*}$$
and then set
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T,{\mathcal {V}}) := \tilde T_k$
. Next, suppose
$\mathsf {swap}_{1\leftrightarrow 2'}(T,{\mathcal {V}}) := \tilde T_k$
. Next, suppose
![]() ${\mathcal {V}}_1,{\mathcal {V}}_2,\dots ,{\mathcal {V}}_l$
are the distinct bars of T containing
${\mathcal {V}}_1,{\mathcal {V}}_2,\dots ,{\mathcal {V}}_l$
are the distinct bars of T containing
![]() $2'$
ordered from bottom to top, so that if
$2'$
ordered from bottom to top, so that if
![]() $i < j$
, then
$i < j$
, then
![]() ${\mathcal {V}}_i$
occurs in smaller-indexed rows than
${\mathcal {V}}_i$
occurs in smaller-indexed rows than
![]() ${\mathcal {V}}_j$
. Finally, let
${\mathcal {V}}_j$
. Finally, let
Example 3.4. Figure 1 shows an example of the successive swaps that are carried out in Definition 3.3 to form
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
.
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
.

Figure 1 An example computation of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. We illustrate each individual operation of the form
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. We illustrate each individual operation of the form
![]() $\mathsf {swap}_{1\leftrightarrow 2'}( -, {\mathcal {V}}, {\mathcal {H}})$
that results in a new tableau (i.e., that does not fall in case (c) of Definition 3.2). The bars
$\mathsf {swap}_{1\leftrightarrow 2'}( -, {\mathcal {V}}, {\mathcal {H}})$
that results in a new tableau (i.e., that does not fall in case (c) of Definition 3.2). The bars
![]() ${\mathcal {H}}_1$
,
${\mathcal {H}}_1$
,
![]() ${\mathcal {H}}_2$
,
${\mathcal {H}}_2$
,
![]() ${\mathcal {H}}_3$
,
${\mathcal {H}}_3$
,
![]() ${\mathcal {H}}_4$
and
${\mathcal {H}}_4$
and
![]() ${\mathcal {H}}_5$
are respectively gray, green, yellow, blue and white; the bars
${\mathcal {H}}_5$
are respectively gray, green, yellow, blue and white; the bars
![]() ${\mathcal {V}}_1$
,
${\mathcal {V}}_1$
,
![]() ${\mathcal {V}}_2$
and
${\mathcal {V}}_2$
and
![]() ${\mathcal {V}}_3$
are respectively orange, pink and red.
${\mathcal {V}}_3$
are respectively orange, pink and red.
Proposition 3.5. If T is a semistandard shifted bar tableau, then
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is a sorted shifted bar tableau of the same shape and weight.
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is a sorted shifted bar tableau of the same shape and weight.
Proof. Let T be a semistandard ShBT. Then
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
has the same shape and weight as T by construction. Since the operation
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
has the same shape and weight as T by construction. Since the operation
![]() $\mathsf {swap}_{1\leftrightarrow 2'}$
affects only the boxes in T filled with
$\mathsf {swap}_{1\leftrightarrow 2'}$
affects only the boxes in T filled with
![]() $1$
or
$1$
or
![]() $2'$
, the result is valid for all semistandard T filled with
$2'$
, the result is valid for all semistandard T filled with
![]() $\{1', 1, 2', 2\}$
if and only if it is valid for those semistandard T filled with only
$\{1', 1, 2', 2\}$
if and only if it is valid for those semistandard T filled with only
![]() $\{1, 2'\}$
. So without loss of generality, assume that the only entries of T are
$\{1, 2'\}$
. So without loss of generality, assume that the only entries of T are
![]() $1$
and
$1$
and
![]() $2'$
. Such a tableau T contains no
$2'$
. Such a tableau T contains no
![]() $2 \times 2$
square of entries, as there is no way to complete the diagram
$2 \times 2$
square of entries, as there is no way to complete the diagram  to a semistandard ShBT. In particular, the only way that T can contain one box strictly northeast of another is if it contains two consecutive boxes on the diagonal:
to a semistandard ShBT. In particular, the only way that T can contain one box strictly northeast of another is if it contains two consecutive boxes on the diagonal:

Thus, the partial order
![]() $\preceq $
on the bars in T where one bar is smaller than (‘before’) another if the first lies entirely (weakly) southeast of the latter is either a total order (if T does not contain two diagonal boxes) or has a unique incomparable pair that come after all other bars of T. This order is compatible with the orders
$\preceq $
on the bars in T where one bar is smaller than (‘before’) another if the first lies entirely (weakly) southeast of the latter is either a total order (if T does not contain two diagonal boxes) or has a unique incomparable pair that come after all other bars of T. This order is compatible with the orders
![]() ${\mathcal {H}}_1, \ldots , {\mathcal {H}}_k$
and
${\mathcal {H}}_1, \ldots , {\mathcal {H}}_k$
and
![]() ${\mathcal {V}}_1, \ldots , {\mathcal {V}}_l$
in Definition 3.3. Moreover, this order extends to every
${\mathcal {V}}_1, \ldots , {\mathcal {V}}_l$
in Definition 3.3. Moreover, this order extends to every
![]() $\{1, 2'\}$
-filled ShBT (semistandard, sorted or otherwise) with the same shape as T, and to every tableau appearing as an intermediate stage in the computation of
$\{1, 2'\}$
-filled ShBT (semistandard, sorted or otherwise) with the same shape as T, and to every tableau appearing as an intermediate stage in the computation of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
.
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
.
Suppose the bars of
![]() $1$
s in T are
$1$
s in T are
![]() ${\mathcal {H}}_1, \ldots , {\mathcal {H}}_k$
and the bars of
${\mathcal {H}}_1, \ldots , {\mathcal {H}}_k$
and the bars of
![]() $2'$
s in T are
$2'$
s in T are
![]() ${\mathcal {V}}_1, \ldots , {\mathcal {V}}_l$
, as in Definition 3.3. Applying any number of
${\mathcal {V}}_1, \ldots , {\mathcal {V}}_l$
, as in Definition 3.3. Applying any number of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}$
operations to T results in a tableau with k bars of
$\mathsf {swap}_{1\leftrightarrow 2'}$
operations to T results in a tableau with k bars of
![]() $1$
s and l bars of
$1$
s and l bars of
![]() $2'$
s. For
$2'$
s. For
![]() $i = 1, \ldots , l$
, let
$i = 1, \ldots , l$
, let
![]() $ T^{(i)} := \mathsf {swap}_{1\leftrightarrow 2'}( \cdots \mathsf {swap}_{1\leftrightarrow 2'}(T, {\mathcal {V}}_1) \cdots , {\mathcal {V}}_i), $
and let the bars of
$ T^{(i)} := \mathsf {swap}_{1\leftrightarrow 2'}( \cdots \mathsf {swap}_{1\leftrightarrow 2'}(T, {\mathcal {V}}_1) \cdots , {\mathcal {V}}_i), $
and let the bars of
![]() $1$
s and
$1$
s and
![]() $2'$
s in
$2'$
s in
![]() $T^{(i)}$
be, respectively,
$T^{(i)}$
be, respectively,
![]() ${\mathcal {H}}^{(i)}_1, \ldots , {\mathcal {H}}^{(i)}_k$
and
${\mathcal {H}}^{(i)}_1, \ldots , {\mathcal {H}}^{(i)}_k$
and
![]() ${\mathcal {V}}^{(i)}_1, \ldots , {\mathcal {V}}^{(i)}_l$
.
${\mathcal {V}}^{(i)}_1, \ldots , {\mathcal {V}}^{(i)}_l$
.
Given a tableau, we will say that a pair of bars A, B is bad if A is filled with
![]() $1$
, B is filled with
$1$
, B is filled with
![]() $2'$
, and A contains a box either directly west or directly south of a box in B as in these pictures:
$2'$
, and A contains a box either directly west or directly south of a box in B as in these pictures:

Each move in (a) and (b) of Definition 3.2 replaces an adjacent pair of bad bars with a non-bad pair. We claim that in the tableau
![]() $T^{(i)}$
, there are no bad pairs involving any of the bars
$T^{(i)}$
, there are no bad pairs involving any of the bars
![]() ${\mathcal {V}}_1^{(i)}, \ldots , {\mathcal {V}}_i^{(i)}$
, except possibly in the case that T has two diagonal boxes and
${\mathcal {V}}_1^{(i)}, \ldots , {\mathcal {V}}_i^{(i)}$
, except possibly in the case that T has two diagonal boxes and
![]() $i = l$
.
$i = l$
.
For
![]() $i = 0$
, this is vacuously true; we proceed by induction. By hypothesis, there are no bad pairs involving
$i = 0$
, this is vacuously true; we proceed by induction. By hypothesis, there are no bad pairs involving
![]() ${\mathcal {V}}_1^{(i - 1)}, \ldots , {\mathcal {V}}_i^{(i - 1)}$
in
${\mathcal {V}}_1^{(i - 1)}, \ldots , {\mathcal {V}}_i^{(i - 1)}$
in
![]() $T^{(i)}$
. Suppose that
$T^{(i)}$
. Suppose that
![]() ${\mathcal {V}}_i = {\mathcal {V}}_i^{(i - 1)}$
lies in column c, and choose j such that
${\mathcal {V}}_i = {\mathcal {V}}_i^{(i - 1)}$
lies in column c, and choose j such that
![]() ${\mathcal {H}}_1^{(i - 1)}, \ldots , {\mathcal {H}}_j^{(i - 1)}$
lie in columns whose indices are greater than or equal to c (i.e., they lie weakly southeast of
${\mathcal {H}}_1^{(i - 1)}, \ldots , {\mathcal {H}}_j^{(i - 1)}$
lie in columns whose indices are greater than or equal to c (i.e., they lie weakly southeast of
![]() ${\mathcal {V}}_i$
in
${\mathcal {V}}_i$
in
![]() $T^{(i - 1)}$
), while
$T^{(i - 1)}$
), while
![]() ${\mathcal {H}}_{j + 1} = {\mathcal {H}}_{j + 1}^{(i - 1)}$
, …,
${\mathcal {H}}_{j + 1} = {\mathcal {H}}_{j + 1}^{(i - 1)}$
, …,
![]() ${\mathcal {H}}_{k} = {\mathcal {H}}_{k}^{(i - 1)}$
lie in columns whose indices are strictly smaller than c. In this setup, it is possible that a single bar of
${\mathcal {H}}_{k} = {\mathcal {H}}_{k}^{(i - 1)}$
lie in columns whose indices are strictly smaller than c. In this setup, it is possible that a single bar of
![]() $1$
s lies in columns with indices both smaller than and greater than or equal to c, but only if
$1$
s lies in columns with indices both smaller than and greater than or equal to c, but only if
![]() $i = l$
and
$i = l$
and
![]() ${\mathcal {V}}_i$
consists of a single diagonal box, as in
${\mathcal {V}}_i$
consists of a single diagonal box, as in  .
.
The first
![]() $j - 1$
swaps in the computation of
$j - 1$
swaps in the computation of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T^{(i - 1)}, {\mathcal {V}}_i)$
do nothing. The jth swap either does nothing (if
$\mathsf {swap}_{1\leftrightarrow 2'}(T^{(i - 1)}, {\mathcal {V}}_i)$
do nothing. The jth swap either does nothing (if
![]() ${\mathcal {H}}_j^{(i - 1)}$
does not contain any boxes in column c) or performs a swap of the type described in Definition 3.2(a). Following this swap, the resulting two bars
${\mathcal {H}}_j^{(i - 1)}$
does not contain any boxes in column c) or performs a swap of the type described in Definition 3.2(a). Following this swap, the resulting two bars
![]() $\tilde {{\mathcal {V}}}_i, \tilde {{\mathcal {H}}}_j$
no longer form a bad pair. Moreover, although the bar
$\tilde {{\mathcal {V}}}_i, \tilde {{\mathcal {H}}}_j$
no longer form a bad pair. Moreover, although the bar
![]() $\tilde {{\mathcal {V}}}_i$
may extend one row below
$\tilde {{\mathcal {V}}}_i$
may extend one row below
![]() ${\mathcal {V}}_i$
, this cannot introduce any new bad pairs involving the bar
${\mathcal {V}}_i$
, this cannot introduce any new bad pairs involving the bar
![]() $\tilde {{\mathcal {V}}}_i$
unless there is a
$\tilde {{\mathcal {V}}}_i$
unless there is a
![]() $1$
to the left of the first box in
$1$
to the left of the first box in
![]() ${\mathcal {H}}_j^{(i - 1)}$
, which only happens if
${\mathcal {H}}_j^{(i - 1)}$
, which only happens if
![]() $i = l$
and
$i = l$
and
![]() ${\mathcal {V}}_i$
consists of a single diagonal box, as in these examples:
${\mathcal {V}}_i$
consists of a single diagonal box, as in these examples:

If, at this stage, there are any further bad pairs involving
![]() $\tilde {{\mathcal {V}}}_i$
, they must come from
$\tilde {{\mathcal {V}}}_i$
, they must come from
![]() $1$
s in boxes directly west of a box in
$1$
s in boxes directly west of a box in
![]() $\tilde {{\mathcal {V}}}_i$
. This can happen if
$\tilde {{\mathcal {V}}}_i$
. This can happen if
![]() $i = l$
and
$i = l$
and
![]() $\tilde {{\mathcal {V}}}_i$
contains a diagonal box
$\tilde {{\mathcal {V}}}_i$
contains a diagonal box  , but otherwise the bar
, but otherwise the bar
![]() ${\mathcal {H}}_{k + 1}$
of
${\mathcal {H}}_{k + 1}$
of
![]() $1$
s in the bad pair must be directly west of and adjacent to the last box in
$1$
s in the bad pair must be directly west of and adjacent to the last box in
![]() $\tilde {{\mathcal {V}}}_i$
. If
$\tilde {{\mathcal {V}}}_i$
. If
![]() $\tilde {{\mathcal {V}}}_i$
has more than one box, then the immediate next swap (of the type in Definition 3.2(b)) removes the box from
$\tilde {{\mathcal {V}}}_i$
has more than one box, then the immediate next swap (of the type in Definition 3.2(b)) removes the box from
![]() $\tilde {{\mathcal {V}}}_i$
that is involved in the bad pair, and the remaining swaps (with
$\tilde {{\mathcal {V}}}_i$
that is involved in the bad pair, and the remaining swaps (with
![]() ${\mathcal {H}}_{j + 2}$
, …) do nothing, leaving a tableau in which the new bar
${\mathcal {H}}_{j + 2}$
, …) do nothing, leaving a tableau in which the new bar
![]() ${\mathcal {V}}^{(i)}_i$
is not involved in any bad pairs. If
${\mathcal {V}}^{(i)}_i$
is not involved in any bad pairs. If
![]() $\tilde {{\mathcal {V}}}_i$
only has a single box, then possibly several moves of type Definition 3.2(b) are required; after these moves, the box occupied by
$\tilde {{\mathcal {V}}}_i$
only has a single box, then possibly several moves of type Definition 3.2(b) are required; after these moves, the box occupied by
![]() ${\mathcal {V}}^{(i)}_i$
was previously occupied by a box labeled
${\mathcal {V}}^{(i)}_i$
was previously occupied by a box labeled
![]() $1$
, so there cannot be any other
$1$
, so there cannot be any other
![]() $1$
s in the same column, and so also in this case,
$1$
s in the same column, and so also in this case,
![]() ${\mathcal {V}}^{(i)}_i$
is not involved in any bad pairs.
${\mathcal {V}}^{(i)}_i$
is not involved in any bad pairs.
Finally, we observe that none of these moves changes any bar of
![]() $1$
s that is east of
$1$
s that is east of
![]() ${\mathcal {V}}^{(i - 1)}_{i - 1}$
(because they are all strictly southeast of
${\mathcal {V}}^{(i - 1)}_{i - 1}$
(because they are all strictly southeast of
![]() ${\mathcal {V}}_i$
) and none of these moves causes any
${\mathcal {V}}_i$
) and none of these moves causes any
![]() $1$
s to appear in a lower row than they previously appeared, so no bad pairs involving
$1$
s to appear in a lower row than they previously appeared, so no bad pairs involving
![]() ${\mathcal {V}}^{(i - 1)}_1 = {\mathcal {V}}^{(i)}_1$
, …,
${\mathcal {V}}^{(i - 1)}_1 = {\mathcal {V}}^{(i)}_1$
, …,
![]() ${\mathcal {V}}^{(i - 1)}_{i - 1} = {\mathcal {V}}^{(i)}_{i - 1}$
are created. This completes the proof of the claim.
${\mathcal {V}}^{(i - 1)}_{i - 1} = {\mathcal {V}}^{(i)}_{i - 1}$
are created. This completes the proof of the claim.
It follows from the preceding argument that either
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
has no bad pairs at all or its shape has two diagonal boxes and there is a bad pair involving the bar of
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
has no bad pairs at all or its shape has two diagonal boxes and there is a bad pair involving the bar of
![]() $2'$
s in the upper diagonal box. By comparing with the definition of sorted tableaux (see Definition 3.1), we find that this is precisely the desired conclusion.
$2'$
s in the upper diagonal box. By comparing with the definition of sorted tableaux (see Definition 3.1), we find that this is precisely the desired conclusion.
3.3 Descending swaps
We now define an inverse to the
![]() $\mathsf {swap}_{1\leftrightarrow 2'}$
operation. In this subsection,
$\mathsf {swap}_{1\leftrightarrow 2'}$
operation. In this subsection,
![]() $\tilde T$
continues to denote an arbitrary ShBT with all entries in
$\tilde T$
continues to denote an arbitrary ShBT with all entries in
![]() $\{1' , 2' , 1 , 2\}$
, which is not necessarily semistandard or sorted.
$\{1' , 2' , 1 , 2\}$
, which is not necessarily semistandard or sorted.
Definition 3.6. Suppose
![]() $\tilde {\mathcal {H}}$
and
$\tilde {\mathcal {H}}$
and
![]() $\tilde {\mathcal {V}}$
are bars in
$\tilde {\mathcal {V}}$
are bars in
![]() $\tilde T$
with unique entries
$\tilde T$
with unique entries
![]() $1$
and
$1$
and
![]() $2'$
, respectively. Below, we define two new bars
$2'$
, respectively. Below, we define two new bars
![]() $ {\mathcal {H}}$
and
$ {\mathcal {H}}$
and
![]() $ {\mathcal {V}}$
whose union
$ {\mathcal {V}}$
whose union
![]() $ {\mathcal {H}}\sqcup {\mathcal {V}}$
occupies the same boxes as
$ {\mathcal {H}}\sqcup {\mathcal {V}}$
occupies the same boxes as
![]() $\tilde {\mathcal {H}}\sqcup \tilde {\mathcal {V}}$
. We then set
$\tilde {\mathcal {H}}\sqcup \tilde {\mathcal {V}}$
. We then set
where
![]() $ T$
is formed from
$ T$
is formed from
![]() $\tilde T$
by replacing
$\tilde T$
by replacing
![]() $\tilde {\mathcal {H}}$
with
$\tilde {\mathcal {H}}$
with
![]() $ {\mathcal {H}}$
and
$ {\mathcal {H}}$
and
![]() $\tilde {\mathcal {V}}$
with
$\tilde {\mathcal {V}}$
with
![]() $ {\mathcal {V}}$
. The rules defining
$ {\mathcal {V}}$
. The rules defining
![]() $ {\mathcal {H}}$
and
$ {\mathcal {H}}$
and
![]() $ {\mathcal {V}}$
are as follows:
$ {\mathcal {V}}$
are as follows:
-
(a) Suppose the first boxes of
 $\tilde {\mathcal {V}}$
and
$\tilde {\mathcal {V}}$
and
 $\tilde {\mathcal {H}}$
are
$\tilde {\mathcal {H}}$
are
 $(i,j)$
and
$(i,j)$
and
 $(i,j+1)$
, respectively. If
$(i,j+1)$
, respectively. If
 $\tilde {\mathcal {V}}$
has more than one box, then we form
$\tilde {\mathcal {V}}$
has more than one box, then we form
 $ {\mathcal {V}}$
from
$ {\mathcal {V}}$
from
 $\tilde {\mathcal {V}}$
by removing its first box and we form
$\tilde {\mathcal {V}}$
by removing its first box and we form
 $ {\mathcal {H}}$
by adding this box to
$ {\mathcal {H}}$
by adding this box to
 $\tilde {\mathcal {H}}$
. If
$\tilde {\mathcal {H}}$
. If
 $\tilde {\mathcal {V}}$
has only one box, then we form
$\tilde {\mathcal {V}}$
has only one box, then we form
 $ {\mathcal {H}}$
by moving
$ {\mathcal {H}}$
by moving
 $\tilde {\mathcal {H}}$
to the left one column and we form
$\tilde {\mathcal {H}}$
to the left one column and we form
 $ {\mathcal {V}}$
by moving
$ {\mathcal {V}}$
by moving
 $\tilde {\mathcal {V}}$
to occupy the last box of
$\tilde {\mathcal {V}}$
to occupy the last box of
 $\tilde {\mathcal {H}}$
. In pictures, we have
$\tilde {\mathcal {H}}$
. In pictures, we have
where the blue boxes are
 $\tilde {\mathcal {H}}$
and
$\tilde {\mathcal {H}}$
and
 ${\mathcal {H}}$
, while the red boxes are
${\mathcal {H}}$
, while the red boxes are
 $\tilde {\mathcal {V}}$
and
$\tilde {\mathcal {V}}$
and
 ${\mathcal {V}}$
.
${\mathcal {V}}$
. -
(b) Suppose the last boxes of
 $\tilde {\mathcal {V}}$
and
$\tilde {\mathcal {V}}$
and
 $\tilde {\mathcal {H}}$
are
$\tilde {\mathcal {H}}$
are
 $(i,j)$
and
$(i,j)$
and
 $(i+1,j)$
, respectively. If
$(i+1,j)$
, respectively. If
 $\tilde {\mathcal {H}}$
has more than one box, then we form
$\tilde {\mathcal {H}}$
has more than one box, then we form
 $ {\mathcal {H}}$
from
$ {\mathcal {H}}$
from
 $\tilde {\mathcal {H}}$
by removing its last box and we form
$\tilde {\mathcal {H}}$
by removing its last box and we form
 $ {\mathcal {V}}$
by adding this box to
$ {\mathcal {V}}$
by adding this box to
 $\tilde {\mathcal {V}}$
. If
$\tilde {\mathcal {V}}$
. If
 $\tilde {\mathcal {H}}$
has only one box, then we form
$\tilde {\mathcal {H}}$
has only one box, then we form
 $ {\mathcal {V}}$
by moving
$ {\mathcal {V}}$
by moving
 $\tilde {\mathcal {V}}$
up one row and we form
$\tilde {\mathcal {V}}$
up one row and we form
 $ {\mathcal {H}}$
by moving
$ {\mathcal {H}}$
by moving
 $\tilde {\mathcal {H}}$
to occupy the first box of
$\tilde {\mathcal {H}}$
to occupy the first box of
 $\tilde {\mathcal {V}}$
. In pictures, we have
$\tilde {\mathcal {V}}$
. In pictures, we have
-
(c) In all other cases, we set
 $ {\mathcal {H}} := \tilde {\mathcal {H}}$
and
$ {\mathcal {H}} := \tilde {\mathcal {H}}$
and
 $ {\mathcal {V}} :=\tilde {\mathcal {V}}$
.
$ {\mathcal {V}} :=\tilde {\mathcal {V}}$
.
Definition 3.7. Suppose
![]() $\tilde {\mathcal {H}}_1,\tilde {\mathcal {H}}_2,\dots ,\tilde {\mathcal {H}}_k$
and
$\tilde {\mathcal {H}}_1,\tilde {\mathcal {H}}_2,\dots ,\tilde {\mathcal {H}}_k$
and
![]() $\tilde {\mathcal {V}}_1,\tilde {\mathcal {V}}_2,\dots ,\tilde {\mathcal {V}}_l$
are the distinct bars of
$\tilde {\mathcal {V}}_1,\tilde {\mathcal {V}}_2,\dots ,\tilde {\mathcal {V}}_l$
are the distinct bars of
![]() $\tilde T$
containing
$\tilde T$
containing
![]() $1$
and
$1$
and
![]() $2'$
, respectively, listed in the orders from Definition 3.3 (i.e., the vertical bars filled with
$2'$
, respectively, listed in the orders from Definition 3.3 (i.e., the vertical bars filled with
![]() $2'$
are ordered from bottom to top and the horizontal bars filled with
$2'$
are ordered from bottom to top and the horizontal bars filled with
![]() $1$
are ordered from right to left). For any single bar
$1$
are ordered from right to left). For any single bar
![]() $\tilde {\mathcal {V}} \in \{\tilde {\mathcal {V}}_1,\tilde {\mathcal {V}}_2,\dots ,\tilde {\mathcal {V}}_l\}$
, inductively define
$\tilde {\mathcal {V}} \in \{\tilde {\mathcal {V}}_1,\tilde {\mathcal {V}}_2,\dots ,\tilde {\mathcal {V}}_l\}$
, inductively define
![]() $( T_k, {\mathcal {V}}_k) := (\tilde T,\tilde {\mathcal {V}})$
and
$( T_k, {\mathcal {V}}_k) := (\tilde T,\tilde {\mathcal {V}})$
and
and then set
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T,\tilde {\mathcal {V}}) := T_0$
. Finally, let
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T,\tilde {\mathcal {V}}) := T_0$
. Finally, let
Example 3.8. Figure 2 shows an example of the successive ‘unswaps’ that are carried out in Definition 3.7 to form
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(T)$
.
$\mathsf {unswap}_{1\leftrightarrow 2'}(T)$
.

Figure 2 An example computation of
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)$
. We illustrate each individual operation of the form
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)$
. We illustrate each individual operation of the form
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}( -, {\mathcal {V}}, {\mathcal {H}})$
that results in a new tableau (i.e., that does not fall in case (c) of Definition 3.6). The bars
$\mathsf {unswap}_{1\leftrightarrow 2'}( -, {\mathcal {V}}, {\mathcal {H}})$
that results in a new tableau (i.e., that does not fall in case (c) of Definition 3.6). The bars
![]() $\tilde {\mathcal {H}}_1$
,
$\tilde {\mathcal {H}}_1$
,
![]() $\tilde {\mathcal {H}}_2$
,
$\tilde {\mathcal {H}}_2$
,
![]() $\tilde {\mathcal {H}}_3$
,
$\tilde {\mathcal {H}}_3$
,
![]() $\tilde {\mathcal {H}}_4$
and
$\tilde {\mathcal {H}}_4$
and
![]() $\tilde {\mathcal {H}}_5$
are respectively gray, green, yellow, blue and white; the bars
$\tilde {\mathcal {H}}_5$
are respectively gray, green, yellow, blue and white; the bars
![]() $\tilde {\mathcal {V}}_1$
,
$\tilde {\mathcal {V}}_1$
,
![]() $\tilde {\mathcal {V}}_2$
and
$\tilde {\mathcal {V}}_2$
and
![]() $\tilde {\mathcal {V}}_3$
are respectively orange, pink and red.
$\tilde {\mathcal {V}}_3$
are respectively orange, pink and red.
Proposition 3.9. If
![]() $\tilde T$
is a sorted shifted bar tableau, then
$\tilde T$
is a sorted shifted bar tableau, then
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)$
is a semistandard shifted bar tableau of the same shape and weight.
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)$
is a semistandard shifted bar tableau of the same shape and weight.
Proof. Let
![]() $\tilde T$
be a sorted shifted bar tableau. By construction,
$\tilde T$
be a sorted shifted bar tableau. By construction,
![]() $\tilde T$
and
$\tilde T$
and
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)$
have the same shape and same weight. First, suppose that
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)$
have the same shape and same weight. First, suppose that
![]() $\tilde T$
does not contain two diagonal boxes. In this case, by comparing the definitions of sorted and semistandard ShBT, we see that rotating
$\tilde T$
does not contain two diagonal boxes. In this case, by comparing the definitions of sorted and semistandard ShBT, we see that rotating
![]() $\tilde T$
by
$\tilde T$
by
![]() $180^\circ $
produces a semistandard ShBT
$180^\circ $
produces a semistandard ShBT
![]() $\tilde T^r$
. Moreover, by comparing Definitions 3.2, 3.3 with Definitions 3.6, 3.7, we see that
$\tilde T^r$
. Moreover, by comparing Definitions 3.2, 3.3 with Definitions 3.6, 3.7, we see that
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(\tilde T^r) = \mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)^r$
, and consequently that
$\mathsf {swap}_{1\leftrightarrow 2'}(\tilde T^r) = \mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)^r$
, and consequently that
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T) = \mathsf {swap}_{1\leftrightarrow 2'}(\tilde T^r)^r$
is a semistandard ShBT.
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T) = \mathsf {swap}_{1\leftrightarrow 2'}(\tilde T^r)^r$
is a semistandard ShBT.
Otherwise, suppose
![]() $\tilde T$
has two diagonal boxes. There are four possible arrangements of the entries the first two diagonals of
$\tilde T$
has two diagonal boxes. There are four possible arrangements of the entries the first two diagonals of
![]() $\tilde T$
, which we illustrate as follows; in all cases,
$\tilde T$
, which we illustrate as follows; in all cases,
![]() $\tilde {{\mathcal {V}}}_l$
is colored in pink and
$\tilde {{\mathcal {V}}}_l$
is colored in pink and
![]() $\tilde {{\mathcal {H}}}_k$
is colored in cyan:
$\tilde {{\mathcal {H}}}_k$
is colored in cyan:
-
(1)

-
(2)

-
(3)

-
(4)

In the first two cases, one has
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T, \tilde {{\mathcal {V}}}_l) = \tilde T$
. In these cases, deleting the unique box of
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T, \tilde {{\mathcal {V}}}_l) = \tilde T$
. In these cases, deleting the unique box of
![]() $\tilde {{\mathcal {V}}}_l$
from
$\tilde {{\mathcal {V}}}_l$
from
![]() $\tilde T$
produces a sorted tableau
$\tilde T$
produces a sorted tableau
![]() $\tilde T - \tilde {{\mathcal {V}}}_l$
with only one diagonal box. Therefore, by the argument in the previous paragraph,
$\tilde T - \tilde {{\mathcal {V}}}_l$
with only one diagonal box. Therefore, by the argument in the previous paragraph,
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {V}}}_l)$
is a semistandard tableau. This tableau becomes
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {V}}}_l)$
is a semistandard tableau. This tableau becomes
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T) = \mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {V}}}_l) \cup \{\tilde {{\mathcal {V}}}_l\}$
when we add back the unique box of
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T) = \mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {V}}}_l) \cup \{\tilde {{\mathcal {V}}}_l\}$
when we add back the unique box of
![]() $\tilde {{\mathcal {V}}}_l$
at the end. Since the added box always contains
$\tilde {{\mathcal {V}}}_l$
at the end. Since the added box always contains
![]() $2'$
, the result is semistandard, as needed.
$2'$
, the result is semistandard, as needed.
In the latter two cases, one has
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T, \tilde {{\mathcal {V}}}_l, \tilde {{\mathcal {H}}}_k) = (\tilde T, \tilde {{\mathcal {V}}}_l)$
(i.e., the very first swap belongs to case (c) of Definition 3.6 and so does not change anything). In these cases, deleting the unique box of
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T, \tilde {{\mathcal {V}}}_l, \tilde {{\mathcal {H}}}_k) = (\tilde T, \tilde {{\mathcal {V}}}_l)$
(i.e., the very first swap belongs to case (c) of Definition 3.6 and so does not change anything). In these cases, deleting the unique box of
![]() $\tilde {{\mathcal {H}}}_k$
produces a sorted tableau
$\tilde {{\mathcal {H}}}_k$
produces a sorted tableau
![]() $\tilde T - \tilde {{\mathcal {H}}}_k$
with only one diagonal box. Again by the argument in the first paragraph of this proof, we deduce that
$\tilde T - \tilde {{\mathcal {H}}}_k$
with only one diagonal box. Again by the argument in the first paragraph of this proof, we deduce that
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {H}}}_k)$
is a semistandard tableau. This tableau becomes
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {H}}}_k)$
is a semistandard tableau. This tableau becomes
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T) = \mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {H}}}_k) \cup \{\tilde {{\mathcal {H}}}_k\}$
when we add back the unique box of
$\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T) = \mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T - \tilde {{\mathcal {H}}}_k) \cup \{\tilde {{\mathcal {H}}}_k\}$
when we add back the unique box of
![]() $\tilde {{\mathcal {H}}}_k$
at the end, which preserves semistandard-ness. This completes the proof.
$\tilde {{\mathcal {H}}}_k$
at the end, which preserves semistandard-ness. This completes the proof.
Theorem 3.10. The operations
![]() $\mathsf {swap}_{1\leftrightarrow 2'}$
and
$\mathsf {swap}_{1\leftrightarrow 2'}$
and
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
are inverse shape- and weight-preserving bijections between semistandard and sorted shifted bar tableaux with all entries in
$\mathsf {unswap}_{1\leftrightarrow 2'}$
are inverse shape- and weight-preserving bijections between semistandard and sorted shifted bar tableaux with all entries in
![]() $\{1', 1, 2', 2\}$
.
$\{1', 1, 2', 2\}$
.
Proof. By Propositions 3.5 and 3.9, the two maps are shape- and weight-preserving and they have the correct domain and codomain. Since each swap preserves the relative orders of the
![]() ${\mathcal {V}}_i$
and of the
${\mathcal {V}}_i$
and of the
![]() ${\mathcal {H}}_j$
, it is immediate from the definitions that
${\mathcal {H}}_j$
, it is immediate from the definitions that
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}(\mathsf {swap}_{1\leftrightarrow 2'}(T)) = T$
for any semistandard ShBT T and
$\mathsf {unswap}_{1\leftrightarrow 2'}(\mathsf {swap}_{1\leftrightarrow 2'}(T)) = T$
for any semistandard ShBT T and
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)) = \tilde T$
for any sorted ShBT
$\mathsf {swap}_{1\leftrightarrow 2'}(\mathsf {unswap}_{1\leftrightarrow 2'}(\tilde T)) = \tilde T$
for any sorted ShBT
![]() $\tilde T$
.
$\tilde T$
.
3.4 Weight reversal
In this subsection, T denotes a fixed choice of sorted ShBT as specified in Definition 3.1, again with all entries in
![]() $\{1' , 2' , 1 , 2\}$
. We partition the bars of this tableau into four kinds of ‘groups’ and then define a weight-reversing involution locally group-by-group.
$\{1' , 2' , 1 , 2\}$
. We partition the bars of this tableau into four kinds of ‘groups’ and then define a weight-reversing involution locally group-by-group.
It will be convenient in what follows to refer to the following conjugation operation on sorted ShBT; all subsequent constructions will be symmetric under conjugation. For this definition, we fix a large positive integer N such that all boxes of T are in
![]() $[N-1]\times [N-1]$
.
$[N-1]\times [N-1]$
.
Definition 3.11. Let
![]() $T^\ast $
be the ShBT formed by applying the transformation
$T^\ast $
be the ShBT formed by applying the transformation
![]() $(i,j) \mapsto (N-j,N-i)$
to the boxes in T and the transformation
$(i,j) \mapsto (N-j,N-i)$
to the boxes in T and the transformation
![]() $v \mapsto 3' - v$
to the entries in T.
$v \mapsto 3' - v$
to the entries in T.
For example,
![]() $T\mapsto T^\ast $
would exchange
$T\mapsto T^\ast $
would exchange

for an appropriate choice of N. Since the examples in (3.1) are conjugate to those in (3.2), this operation does indeed give another sorted ShBT.
Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be bars in T. We write
$\mathcal {B}$
be bars in T. We write
![]() $\mathcal {A} \approx \mathcal {B}$
if the two bars have unprimed entries in the same column or have primed entries in the same row. We also write
$\mathcal {A} \approx \mathcal {B}$
if the two bars have unprimed entries in the same column or have primed entries in the same row. We also write
![]() $\mathcal {A} \approx \mathcal {B}$
if T has two diagonal boxes
$\mathcal {A} \approx \mathcal {B}$
if T has two diagonal boxes
![]() $(i,i)$
and
$(i,i)$
and
![]() $(i+1,i+1)$
, the bar
$(i+1,i+1)$
, the bar
![]() $\mathcal {A}$
consists of one of the two diagonal boxes (and no off-diagonal boxes), and the bar
$\mathcal {A}$
consists of one of the two diagonal boxes (and no off-diagonal boxes), and the bar
![]() $\mathcal {B}$
contains the box
$\mathcal {B}$
contains the box
![]() $(i,i+1)$
, or vice-versa. An equivalence class for the transitive closure of
$(i,i+1)$
, or vice-versa. An equivalence class for the transitive closure of
![]() $\approx $
is a two-row-group (respectively, a two-column-group) if the class contains at least two bars in T and the bars in the class fit entirely in two rows (respectively, columns), with the following exception. It is possible to have classes that consist of exactly three boxes (in two or three bars), two of which are diagonal, and which therefore fit entirely into two rows and also into two columns; for example,
$\approx $
is a two-row-group (respectively, a two-column-group) if the class contains at least two bars in T and the bars in the class fit entirely in two rows (respectively, columns), with the following exception. It is possible to have classes that consist of exactly three boxes (in two or three bars), two of which are diagonal, and which therefore fit entirely into two rows and also into two columns; for example,

We refer to these classes as two-row-groups (respectively, two-column-groups) if and only if their nondiagonal entry is unprimed (respectively, primed). Thus, of the three tableaux in (3.5), the first is a two-row-group and the others are two-column-groups.
Here is our first nontrivial observation about these equivalence classes.
Proposition 3.12. Every non-singleton equivalence class for the transitive closure of
![]() $\approx $
is a two-row-group or a two-column-group. Every two-row-group is of one of the forms
$\approx $
is a two-row-group or a two-column-group. Every two-row-group is of one of the forms

with some division into bars. That is, the boxes in the union making up a two-row-group are either of the form
or of the form
and every two-column-group is conjugate to one of these. Also, if a two-row-group has two diagonal boxes (marked x, y in the illustration), then these are filled in one of the following six ways:

and in a two-column-group, the options are conjugate to these.
Proof. First, consider the equivalence classes that consist of all unprimed bars. In this case, if
![]() $\mathcal {A} \approx \mathcal {B}$
, then the relations satisfied by the entries of a sorted ShBT imply that when the bar
$\mathcal {A} \approx \mathcal {B}$
, then the relations satisfied by the entries of a sorted ShBT imply that when the bar
![]() $\mathcal {A}$
is filled with
$\mathcal {A}$
is filled with
![]() $1$
and lies in row i, the bar
$1$
and lies in row i, the bar
![]() $\mathcal {B}$
must be filled with
$\mathcal {B}$
must be filled with
![]() $2$
s and lie in row
$2$
s and lie in row
![]() $i + 1$
, and conversely. Hence, the entire equivalence class is restricted to two consecutive rows i and
$i + 1$
, and conversely. Hence, the entire equivalence class is restricted to two consecutive rows i and
![]() $i + 1$
, with row i containing
$i + 1$
, with row i containing
![]() $1$
s and row
$1$
s and row
![]() $i + 1$
containing
$i + 1$
containing
![]() $2$
s. Furthermore, row
$2$
s. Furthermore, row
![]() $i + 1$
cannot extend to the right of row i because the only way to complete the diagram
$i + 1$
cannot extend to the right of row i because the only way to complete the diagram

to a valid sorted ShBT is if the box ![]() is filled with a
is filled with a
![]() $1$
. Similarly, row i cannot extend to the left of row
$1$
. Similarly, row i cannot extend to the left of row
![]() $i + 1$
except in the case
$i + 1$
except in the case

where it does so at the diagonal. The case of equivalence classes containing all primed bars is the conjugate of this case.
We now consider the case of equivalence classes that contain both primed and unprimed bars. In this case, the exceptional rule defining
![]() $\approx $
must come into play: the tableau T must have two diagonal boxes
$\approx $
must come into play: the tableau T must have two diagonal boxes
![]() $(i, i)$
and
$(i, i)$
and
![]() $(i + 1, i + 1)$
for some i, at least one of which must be a bar unto itself. Any skew shifted shape that contains
$(i + 1, i + 1)$
for some i, at least one of which must be a bar unto itself. Any skew shifted shape that contains
![]() $(i, i)$
and
$(i, i)$
and
![]() $(i + 1, i + 1)$
also contains
$(i + 1, i + 1)$
also contains
![]() $(i, i + 1)$
; up to conjugacy, we may assume that the box
$(i, i + 1)$
; up to conjugacy, we may assume that the box
![]() $(i, i + 1)$
is filled with an unprimed entry. In fact, this unprimed entry must be
$(i, i + 1)$
is filled with an unprimed entry. In fact, this unprimed entry must be
![]() $1$
: no tableau of the form
$1$
: no tableau of the form  with entries in
with entries in
![]() $\{1', 2', 1, 2\}$
is a sorted ShBT. Let
$\{1', 2', 1, 2\}$
is a sorted ShBT. Let
![]() $\mathcal {A}$
be the bar containing the box
$\mathcal {A}$
be the bar containing the box
![]() $(i, i + 1)$
. By hypothesis, one of the two boxes
$(i, i + 1)$
. By hypothesis, one of the two boxes
![]() $(i, i)$
and
$(i, i)$
and
![]() $(i + 1, i + 1)$
must belong to a one-box bar that is filled with either
$(i + 1, i + 1)$
must belong to a one-box bar that is filled with either
![]() $1'$
or
$1'$
or
![]() $2'$
.
$2'$
.
First, suppose that the box
![]() $(i, i)$
is a singleton bar
$(i, i)$
is a singleton bar
![]() $\mathcal {B}$
. In this case, its only relation under
$\mathcal {B}$
. In this case, its only relation under
![]() $\approx $
is
$\approx $
is
![]() $\mathcal {A} \approx \mathcal {B}$
, and the box
$\mathcal {A} \approx \mathcal {B}$
, and the box
![]() $(i + 1, i + 1)$
could either be filled with
$(i + 1, i + 1)$
could either be filled with
![]() $2'$
(if
$2'$
(if
![]() $\mathcal {B}$
is also filled with
$\mathcal {B}$
is also filled with
![]() $2'$
) or with
$2'$
) or with
![]() $2$
. In the case that
$2$
. In the case that
![]() $(i + 1, i + 1)$
is filled with
$(i + 1, i + 1)$
is filled with
![]() $2'$
, its unique relation under
$2'$
, its unique relation under
![]() $\approx $
is with
$\approx $
is with
![]() $\mathcal {A}$
, and so in either case, the logic of the previous paragraph applies to conclude that all boxes in the equivalence class belong to rows i and
$\mathcal {A}$
, and so in either case, the logic of the previous paragraph applies to conclude that all boxes in the equivalence class belong to rows i and
![]() $i + 1$
.
$i + 1$
.
Second, suppose that box
![]() $(i + 1, i + 1)$
is filled with a primed entry. By Definition 3.1, it follows that this entry is
$(i + 1, i + 1)$
is filled with a primed entry. By Definition 3.1, it follows that this entry is
![]() $2'$
and that
$2'$
and that
![]() $(i, i)$
is either filled with
$(i, i)$
is either filled with
![]() $1$
or with
$1$
or with
![]() $2'$
. In the former case, the equivalence class again belongs to two rows, for the same reasons. In the latter case, it turns out that the box
$2'$
. In the former case, the equivalence class again belongs to two rows, for the same reasons. In the latter case, it turns out that the box
![]() $(i, i)$
must also be a bar unto itself because it is not possible to complete the diagram
$(i, i)$
must also be a bar unto itself because it is not possible to complete the diagram

to a sorted ShBT. This establishes all of our claims about two-row-groups. The case of two-column-groups is equivalent after taking conjugates everywhere.
Now suppose
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are bars within T that do not belong to any two-row- or two-column-group. We write
$\mathcal {B}$
are bars within T that do not belong to any two-row- or two-column-group. We write
![]() $\mathcal {A} \sim \mathcal {B}$
if
$\mathcal {A} \sim \mathcal {B}$
if
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are adjacent unprimed bars (in the same row) or adjacent primed bars (in the same column). We also write
$\mathcal {B}$
are adjacent unprimed bars (in the same row) or adjacent primed bars (in the same column). We also write
![]() $\mathcal {A} \sim \mathcal {B}$
if the bars are adjacent and one bar consists of a single box on the diagonal. An equivalence class for the transitive closure of
$\mathcal {A} \sim \mathcal {B}$
if the bars are adjacent and one bar consists of a single box on the diagonal. An equivalence class for the transitive closure of
![]() $\sim $
is a one-row-group (respectively, one-column-group) if the bars in the class fit entirely in one row (respectively, one column), with the exception that an equivalence class containing a single one-box bar is a one-row-group if its entry is unprimed and a one-column-group if its entry is primed.
$\sim $
is a one-row-group (respectively, one-column-group) if the bars in the class fit entirely in one row (respectively, one column), with the exception that an equivalence class containing a single one-box bar is a one-row-group if its entry is unprimed and a one-column-group if its entry is primed.
Proposition 3.13. Every equivalence class for the transitive closure of
![]() $\sim $
is either a one-row- or one-column-group. Every one-row-group is of one of forms (with some division into bars)
$\sim $
is either a one-row- or one-column-group. Every one-row-group is of one of forms (with some division into bars)
where in all cases the number of
![]() $1$
s or
$1$
s or
![]() $2$
s might be
$2$
s might be
![]() $0$
, and the latter two cases occur only when the leftmost box is on the diagonal; and every one-column-group is conjugate to one of these.
$0$
, and the latter two cases occur only when the leftmost box is on the diagonal; and every one-column-group is conjugate to one of these.
Proof. The case of equivalence classes that do not contain any diagonal box is straightforward from the definition. If a tableau T contains two diagonal boxes
![]() $(i, i)$
and
$(i, i)$
and
![]() $(i + 1, i + 1)$
, then at least one of them belongs to a two-row- or two-column-group with
$(i + 1, i + 1)$
, then at least one of them belongs to a two-row- or two-column-group with
![]() $(i, i + 1)$
and so does not belong to any one-row- or one-column-group. Thus, we may restrict our attention to the case of tableaux with a single diagonal box, and the equivalence class that contains that box. In particular, we must show that the diagonal box cannot be in the same group with its neighbors to the east and south simultaneously. It is a simple finite computation to check that in all
$(i, i + 1)$
and so does not belong to any one-row- or one-column-group. Thus, we may restrict our attention to the case of tableaux with a single diagonal box, and the equivalence class that contains that box. In particular, we must show that the diagonal box cannot be in the same group with its neighbors to the east and south simultaneously. It is a simple finite computation to check that in all
![]() $30$
sorted ShBT of shape
$30$
sorted ShBT of shape

at least one of the neighbors of the diagonal box belongs to a two-row- or two-column-group. Then the result follows immediately.
We now describe a collection of operations that can be applied locally to a given group. These operations will all reverse the weight of the group, while globally replacing the sorted ShBT with another sorted ShBT. They will also have predictable effects on which diagonal boxes carry primes (which will be important when considering the symmetry of the generating function
![]() $j\hspace {-0.1mm}p_{\lambda /\mu }$
).
$j\hspace {-0.1mm}p_{\lambda /\mu }$
).
First, consider a one-row-group. We define an operation called toggling the labels of the group, as follows. If the group has a (necessarily unique) primed diagonal entry, then remove its prime. Suppose this results in a group with p bars containing
![]() $1$
and q bars containing
$1$
and q bars containing
![]() $2$
. We order these bars from left to right in the usual way, unless there is a one-box bar on the diagonal containing
$2$
. We order these bars from left to right in the usual way, unless there is a one-box bar on the diagonal containing
![]() $2$
. In the latter case, we consider the diagonal bar to be the last bar in the group and order the remaining bars from left to right. Finally, relabel these
$2$
. In the latter case, we consider the diagonal bar to be the last bar in the group and order the remaining bars from left to right. Finally, relabel these
![]() $p+q$
bars so that first q bars contain
$p+q$
bars so that first q bars contain
![]() $1$
and the last p bars contain
$1$
and the last p bars contain
![]() $2$
, and then add back a prime to the one-box diagonal bar if this was removed earlier. For example, this would give
$2$
, and then add back a prime to the one-box diagonal bar if this was removed earlier. For example, this would give

Toggling the labels in a one-column-group is precisely the conjugate operation; for example, toggling the labels transforms

Next consider a two-row-group with boxes in rows i and
![]() $i+1$
. First, assume the group has at most one diagonal box. (In this case, by Proposition 3.12, all bars in the group are filled with unprimed entries.) We define a weight-reversing operation called toggling the bar divisions in the group, as follows. We form another two-row-group with the same entries that has a bar division between columns j and
$i+1$
. First, assume the group has at most one diagonal box. (In this case, by Proposition 3.12, all bars in the group are filled with unprimed entries.) We define a weight-reversing operation called toggling the bar divisions in the group, as follows. We form another two-row-group with the same entries that has a bar division between columns j and
![]() $j+1$
in row i (respectively,
$j+1$
in row i (respectively,
![]() $i+1$
) if and only if a bar division occurs between columns j and
$i+1$
) if and only if a bar division occurs between columns j and
![]() $j+1$
in row
$j+1$
in row
![]() $i+1$
(respectively, i) in the starting group, as in
$i+1$
(respectively, i) in the starting group, as in

This operation is obviously weight-reversing.
The situation of two-row-groups that contain two diagonal boxes is more complicated. We again introduce a notion of toggling the bar divisions that is not necessarily weight-reversing (or even well defined on ShBT); it will be used as one step in the final weight-reversing map of Definition 3.14 below. Given a two-row-group with two diagonal boxes
![]() $(i,i)$
and
$(i,i)$
and
![]() $(i,i+1)$
, we define the operation of toggling the bar divisions as above, except that we mandate that boxes
$(i,i+1)$
, we define the operation of toggling the bar divisions as above, except that we mandate that boxes
![]() $(i,i)$
and
$(i,i)$
and
![]() $(i,i+1)$
belong to the same bar in the toggled group if and only if they belong to the same bar in the original group – for example, as in
$(i,i+1)$
belong to the same bar in the toggled group if and only if they belong to the same bar in the original group – for example, as in

If the box
![]() $(i+1,i+1)$
contains
$(i+1,i+1)$
contains
![]() $2'$
and box
$2'$
and box
![]() $(i+1,i+2)$
is part of the group, then our toggling operation could result in a tableau that is not a valid ShBT; in practice, we will never apply our operation when this case would arise.
$(i+1,i+2)$
is part of the group, then our toggling operation could result in a tableau that is not a valid ShBT; in practice, we will never apply our operation when this case would arise.
There are analogous toggling operations for two-column-groups. They are precisely the conjugate (in the sense of Definition 3.11) of the operations defined above. For example, to toggle the bar divisions in a two-column-group transforms

We now combine all of these local transformations into the following weight-reversing operator.
Definition 3.14. Let T be a sorted shifted bar tableau with all entries in
![]() $\{1' , 2' , 1 , 2\}$
. We form another shifted bar tableau, denoted
$\{1' , 2' , 1 , 2\}$
. We form another shifted bar tableau, denoted
![]() $\mathsf {reverse\_weight}(T)$
, by transforming T as follows:
$\mathsf {reverse\_weight}(T)$
, by transforming T as follows:
-
1. First, toggle the labels in each one-row-group and one-column-group. Then toggle the bar divisions in each two-row-group and two-column-group, excluding the unique group with two diagonal boxes (if this exists).
-
2. Suppose T has a group with two diagonal boxes. If this is a two-row-group with diagonal boxes
 $(i,i)$
and
$(i,i)$
and
 $(i+1,i+1)$
, then proceed according to the following cases:
$(i+1,i+1)$
, then proceed according to the following cases:-
(R1) If
 $(i,i)$
is a one-box bar containing
$(i,i)$
is a one-box bar containing
 $1$
(respectively,
$1$
(respectively,
 $2'$
) and the entry in
$2'$
) and the entry in
 $(i+1,i+1)$
is
$(i+1,i+1)$
is
 $2$
, then toggle the bar divisions and change the entry in
$2$
, then toggle the bar divisions and change the entry in
 $(i,i)$
to
$(i,i)$
to
 $2'$
(respectively,
$2'$
(respectively,
 $1$
):
$1$
):
-
(R2) Suppose
 $(i,i)$
is a one-box bar containing
$(i,i)$
is a one-box bar containing
 $1'$
, the boxes
$1'$
, the boxes
 $(i,i+1)$
and
$(i,i+1)$
and
 $(i,i+2)$
belong to the same bar, and
$(i,i+2)$
belong to the same bar, and
 $(i+1,i+2)$
is in the group. In this case, the entry in
$(i+1,i+2)$
is in the group. In this case, the entry in
 $(i+1,i+1)$
is necessarily
$(i+1,i+1)$
is necessarily
 $2$
by Proposition 3.12. First, change the entry in
$2$
by Proposition 3.12. First, change the entry in
 $(i,i)$
to
$(i,i)$
to
 $1$
and merge this box into the bar of
$1$
and merge this box into the bar of
 $(i,i+1)$
. Next, toggle the bar divisions. Finally, change
$(i,i+1)$
. Next, toggle the bar divisions. Finally, change
 $(i+1,i+1)$
to a one-box bar containing
$(i+1,i+1)$
to a one-box bar containing
 $2'$
:
$2'$
:
-
(R3) Suppose
 $(i+1,i+1)$
is a one-box bar containing
$(i+1,i+1)$
is a one-box bar containing
 $2'$
, the boxes
$2'$
, the boxes
 $(i,i)$
and
$(i,i)$
and
 $(i,i+1)$
belong to the same bar (necessarily containing
$(i,i+1)$
belong to the same bar (necessarily containing
 $1$
), and
$1$
), and
 $(i+1,i+2)$
is in the group. First, change the entry in
$(i+1,i+2)$
is in the group. First, change the entry in
 $(i+1,i+1)$
to
$(i+1,i+1)$
to
 $2$
and merge this box into the bar of
$2$
and merge this box into the bar of
 $(i+1,i+2)$
. Next, toggle the bar divisions. Finally, change
$(i+1,i+2)$
. Next, toggle the bar divisions. Finally, change
 $(i,i)$
to a one-box bar containing
$(i,i)$
to a one-box bar containing
 $1'$
. This is illustrated by reversing the direction of the example in case (R2).
$1'$
. This is illustrated by reversing the direction of the example in case (R2). -
(R4) Suppose
 $(i,i)$
is a one-box bar containing
$(i,i)$
is a one-box bar containing
 $1'$
, but the boxes
$1'$
, but the boxes
 $(i,i+1)$
and
$(i,i+1)$
and
 $(i,i+2)$
do not belong to the same bar or the box
$(i,i+2)$
do not belong to the same bar or the box
 $(i+1,i+2)$
is not part of the group. In this case, the entry in
$(i+1,i+2)$
is not part of the group. In this case, the entry in
 $(i+1,i+1)$
is necessarily
$(i+1,i+1)$
is necessarily
 $2$
by Proposition 3.12. Then toggle the bar divisions and change the entries in both
$2$
by Proposition 3.12. Then toggle the bar divisions and change the entries in both
 $(i,i)$
and
$(i,i)$
and
 $(i+1,i+1)$
to
$(i+1,i+1)$
to
 $2'$
:
$2'$
:
or

-
(R5) If
 $(i,i)$
and
$(i,i)$
and
 $(i+1,i+1)$
are both one-box bars containing
$(i+1,i+1)$
are both one-box bars containing
 $2'$
, then change the entries in
$2'$
, then change the entries in
 $(i,i)$
and
$(i,i)$
and
 $(i+1,i+1)$
to
$(i+1,i+1)$
to
 $1'$
and
$1'$
and
 $2$
, respectively, and toggle the bar divisions. This is illustrated by reversing the examples in case (R4).
$2$
, respectively, and toggle the bar divisions. This is illustrated by reversing the examples in case (R4). -
(R6) If none of (R1)–(R5) apply, just toggle the bar divisions in the two-row-group.
If the two diagonal boxes instead occur in a two-column-group, then replace this group by its conjugate, transform that two-row-group according to cases (R1)–(R6), and finally conjugate the result. Explicitly, this means that if there is a two-column-group with diagonal boxes
 $(i-1,i-1)$
and
$(i-1,i-1)$
and
 $(i,i)$
, then we proceed according to the following cases (illustrated in Figure 3):
$(i,i)$
, then we proceed according to the following cases (illustrated in Figure 3):
Figure 3 The special cases (C1), (C2)–(C3), and (C4)–(C5) of Definition 3.14.
-
(C1) If
 $(i,i)$
is a one-box bar containing
$(i,i)$
is a one-box bar containing
 $2'$
(respectively,
$2'$
(respectively,
 $1$
) and the entry in
$1$
) and the entry in
 $(i-1,i-1)$
is
$(i-1,i-1)$
is
 $1'$
, then toggle the bar divisions and change the entry in
$1'$
, then toggle the bar divisions and change the entry in
 $(i,i)$
to
$(i,i)$
to
 $1$
(respectively,
$1$
(respectively,
 $2'$
).
$2'$
). -
(C2) Suppose
 $(i,i)$
is a one-box bar containing
$(i,i)$
is a one-box bar containing
 $2$
, boxes
$2$
, boxes
 $(i-1,i)$
and
$(i-1,i)$
and
 $(i-2,i)$
belong to the same bar, and
$(i-2,i)$
belong to the same bar, and
 $(i-1,i-2)$
is in the group. In this case, the entry in
$(i-1,i-2)$
is in the group. In this case, the entry in
 $(i-1,i-1)$
is necessarily
$(i-1,i-1)$
is necessarily
 $1'$
by Proposition 3.12. First, change the entry in
$1'$
by Proposition 3.12. First, change the entry in
 $(i,i)$
to
$(i,i)$
to
 $2'$
and merge this box into the bar of
$2'$
and merge this box into the bar of
 $(i-1,i)$
. Next, toggle the bar divisions. Finally, change
$(i-1,i)$
. Next, toggle the bar divisions. Finally, change
 $(i-1,i-1)$
to a one-box bar containing
$(i-1,i-1)$
to a one-box bar containing
 $1$
.
$1$
. -
(C3) Suppose
 $(i-1,i-1)$
is a one-box bar containing
$(i-1,i-1)$
is a one-box bar containing
 $1$
, the boxes
$1$
, the boxes
 $(i,i)$
and
$(i,i)$
and
 $(i-1,i)$
belong to the same bar (necessarily containing
$(i-1,i)$
belong to the same bar (necessarily containing
 $2'$
), and
$2'$
), and
 $(i-2,i-1)$
is in the group. First, change the entry in
$(i-2,i-1)$
is in the group. First, change the entry in
 $(i-1,i-1)$
to
$(i-1,i-1)$
to
 $1'$
and merge this box into the bar of
$1'$
and merge this box into the bar of
 $(i-2,i-1)$
. Next, toggle the bar divisions. Finally, change
$(i-2,i-1)$
. Next, toggle the bar divisions. Finally, change
 $(i,i)$
to a one-box bar containing
$(i,i)$
to a one-box bar containing
 $2$
.
$2$
. -
(C4) Suppose
 $(i,i)$
is a one-box bar containing
$(i,i)$
is a one-box bar containing
 $2$
, but the boxes
$2$
, but the boxes
 $(i-1,i)$
and
$(i-1,i)$
and
 $(i-2,i)$
do not belong to the same bar or the box
$(i-2,i)$
do not belong to the same bar or the box
 $(i-2,i-1)$
is not part of the group. In this case, the entry in
$(i-2,i-1)$
is not part of the group. In this case, the entry in
 $(i-1,i-1)$
is necessarily
$(i-1,i-1)$
is necessarily
 $1'$
by Proposition 3.12. Then toggle the bar divisions and change the entries in both
$1'$
by Proposition 3.12. Then toggle the bar divisions and change the entries in both
 $(i,i)$
and
$(i,i)$
and
 $(i-1,i-1)$
to
$(i-1,i-1)$
to
 $1$
.
$1$
. -
(C5) If
 $(i,i)$
and
$(i,i)$
and
 $(i-1,i-1)$
are both one-box bars containing
$(i-1,i-1)$
are both one-box bars containing
 $1$
, then change the entries in
$1$
, then change the entries in
 $(i,i)$
and
$(i,i)$
and
 $(i-1,i-1)$
to
$(i-1,i-1)$
to
 $2$
and
$2$
and
 $1'$
, respectively, and toggle the bar divisions.
$1'$
, respectively, and toggle the bar divisions. -
(C6) If none of (C1)–(C5) apply, just toggle the bar divisions in the two-column-group.
-
Theorem 3.15. The operation
![]() $\mathsf {reverse\_weight}$
is a shape-preserving and weight-reversing involution of the set of sorted shifted bar tableaux with all entries in
$\mathsf {reverse\_weight}$
is a shape-preserving and weight-reversing involution of the set of sorted shifted bar tableaux with all entries in
![]() $\{1',1,2',2\}$
.
$\{1',1,2',2\}$
.
Proof. By construction, every bar in a sorted ShBT belongs to a group, and each local transformation (toggling the labels on one-row- and one-column-groups, toggling the bar divisions on two-row- and two-column-groups that contain at most one diagonal box, applying rules (R1)–(R6) and (C1)–(C6) to two-row- and two-column-groups that contain two diagonal boxes) reverses the weight and preserves the shape of the group on which it acts, so the map
![]() $\mathsf {reverse\_weight}$
is weight-reversing and shape-preserving. It remains to show first that
$\mathsf {reverse\_weight}$
is weight-reversing and shape-preserving. It remains to show first that
![]() $\mathsf {reverse\_weight}$
is well defined (i.e., that for any sorted ShBT T, the image
$\mathsf {reverse\_weight}$
is well defined (i.e., that for any sorted ShBT T, the image
![]() $\mathsf {reverse\_weight}(T)$
is also a sorted ShBT), and second that the groups of
$\mathsf {reverse\_weight}(T)$
is also a sorted ShBT), and second that the groups of
![]() $\mathsf {reverse\_weight}(T)$
are supported on the same boxes as the groups of T. Since each local transformation is an involution by definition, this will establish that
$\mathsf {reverse\_weight}(T)$
are supported on the same boxes as the groups of T. Since each local transformation is an involution by definition, this will establish that
![]() $\mathsf {reverse\_weight}$
is an involution.
$\mathsf {reverse\_weight}$
is an involution.
Given any group in T, its image under the appropriate local transformation is compatible with the definition of sorted tableaux. Thus, to check that
![]() $\mathsf {reverse\_weight}$
is well defined as a map from sorted ShBT to sorted ShBT, we must establish that (1) adjacent boxes in different groups satisfy the correct order relation, and (2) if there are two diagonal boxes, then they and the box between them are validly filled.
$\mathsf {reverse\_weight}$
is well defined as a map from sorted ShBT to sorted ShBT, we must establish that (1) adjacent boxes in different groups satisfy the correct order relation, and (2) if there are two diagonal boxes, then they and the box between them are validly filled.
We begin with some basic observations. All of the local transformations have the property that if a nondiagonal box
![]() $(i, j)$
in a sorted ShBT T is filled with a primed (respectively, unprimed) entry, then the box
$(i, j)$
in a sorted ShBT T is filled with a primed (respectively, unprimed) entry, then the box
![]() $(i, j)$
in
$(i, j)$
in
![]() $\mathsf {reverse\_weight}(T)$
is also filled with a primed (respectively, unprimed) entry. Moreover, every nondiagonal box of a one- or two-column-group is filled with a primed entry, and every nondiagonal box of a one- or two-row-group is filled with an unprimed entry. Therefore, to prove that
$\mathsf {reverse\_weight}(T)$
is also filled with a primed (respectively, unprimed) entry. Moreover, every nondiagonal box of a one- or two-column-group is filled with a primed entry, and every nondiagonal box of a one- or two-row-group is filled with an unprimed entry. Therefore, to prove that
![]() $\mathsf {reverse\_weight}(T)$
is a sorted ShBT, we need only check conditions at the diagonal and between groups of the same ‘type’ (both row or both column). We handle the second case first.
$\mathsf {reverse\_weight}(T)$
is a sorted ShBT, we need only check conditions at the diagonal and between groups of the same ‘type’ (both row or both column). We handle the second case first.
In the case of two-row-groups that do not contain two diagonal boxes, each box is filled with the same number after toggling the bar divisions as it was before (only the division of these boxes into bars changes), and the new bars are still connected under
![]() $\approx $
(a division between bars that fails to disconnect the group still fails to disconnect the group when it switches rows). Thus, the operation
$\approx $
(a division between bars that fails to disconnect the group still fails to disconnect the group when it switches rows). Thus, the operation
![]() $\mathsf {reverse\_weight}$
preserves the order relation between groups of this type.
$\mathsf {reverse\_weight}$
preserves the order relation between groups of this type.
Two one-row-groups cannot have any adjacent boxes: if a box in one were directly below a box in the other, then these two boxes would belong to a two-row-group (and so, by definition, could not belong to one-row-groups), while if a box in one were directly to the right of a box in the other, then these two boxes would belong to the same one-row-group.
Finally, suppose that
![]() $\mathcal {A}$
is a two-row-group occupying rows i and
$\mathcal {A}$
is a two-row-group occupying rows i and
![]() $i + 1$
and
$i + 1$
and
![]() $\mathcal {B}$
is a one-row-group that contains a box adjacent to a box in
$\mathcal {B}$
is a one-row-group that contains a box adjacent to a box in
![]() $\mathcal {A}$
. These adjacent boxes must lie in the same row (rather than the same column) because otherwise the box in the one-row-group would belong instead to a two-row-group. It follows as in the proof of Proposition 3.12 that if the boxes in the one-row-group
$\mathcal {A}$
. These adjacent boxes must lie in the same row (rather than the same column) because otherwise the box in the one-row-group would belong instead to a two-row-group. It follows as in the proof of Proposition 3.12 that if the boxes in the one-row-group
![]() $\mathcal {B}$
are to the right of the boxes in
$\mathcal {B}$
are to the right of the boxes in
![]() $\mathcal {A}$
, then it must lie in row i, because there is no way to complete
$\mathcal {A}$
, then it must lie in row i, because there is no way to complete

to a sorted ShBT. Similarly, if the boxes in
![]() $\mathcal {B}$
lie to the left of the boxes in
$\mathcal {B}$
lie to the left of the boxes in
![]() $\mathcal {A}$
, then they must lie in row
$\mathcal {A}$
, then they must lie in row
![]() $i + 1$
. (In the latter case, there is an additional consideration concerning the situation in which the one-row-block consists of a single diagonal box, but in this case, the putative one-row-block would actually be part of the two-row-block.) In the first situation, after applying
$i + 1$
. (In the latter case, there is an additional consideration concerning the situation in which the one-row-block consists of a single diagonal box, but in this case, the putative one-row-block would actually be part of the two-row-block.) In the first situation, after applying
![]() $\mathsf {reverse\_weight}$
, the box in the two-row-group is still filled with
$\mathsf {reverse\_weight}$
, the box in the two-row-group is still filled with
![]() $1$
and still to the left of the box in the one-row-group (which will either end up filled with
$1$
and still to the left of the box in the one-row-group (which will either end up filled with
![]() $1$
or
$1$
or
![]() $2$
), and in the second case, the box in the two-row-group is still filled with
$2$
), and in the second case, the box in the two-row-group is still filled with
![]() $2$
and still to the right of the box in the one-row-group. Thus, the order relations are preserved in both cases. The situation for one- and two-column-groups is precisely the conjugate. This completes the proof that
$2$
and still to the right of the box in the one-row-group. Thus, the order relations are preserved in both cases. The situation for one- and two-column-groups is precisely the conjugate. This completes the proof that
![]() $\mathsf {reverse\_weight}(T)$
obeys the order relations of a sorted ShBT among all pairs of adjacent boxes except possibly those at the diagonal (in the case that T contains two diagonal boxes).
$\mathsf {reverse\_weight}(T)$
obeys the order relations of a sorted ShBT among all pairs of adjacent boxes except possibly those at the diagonal (in the case that T contains two diagonal boxes).
Now consider the collection of sorted ShBT with two diagonal boxes in positions
![]() $(i, i)$
and
$(i, i)$
and
![]() $(i + 1, i + 1)$
. There are twelve possible fillings of the three boxes
$(i + 1, i + 1)$
. There are twelve possible fillings of the three boxes
![]() $(i, i)$
,
$(i, i)$
,
![]() $(i, i + 1)$
,
$(i, i + 1)$
,
![]() $(i + 1, i + 1)$
: six of them are shown in the statement of Proposition 3.12, and the other six are conjugate to these. In the cases
$(i + 1, i + 1)$
: six of them are shown in the statement of Proposition 3.12, and the other six are conjugate to these. In the cases

and their conjugates, it is easy to see that the three boxes must belong to a single two-row-group. (The nontrivial cases are the first and fourth; the proof of Proposition 3.12 shows explicitly that in the box
![]() $(i, i)$
must be a one-bar group in the fourth case, and the proof in the first case is identical.) The boxes directly below this group (if there are any) can only be filled with primed entries; after applying
$(i, i)$
must be a one-bar group in the fourth case, and the proof in the first case is identical.) The boxes directly below this group (if there are any) can only be filled with primed entries; after applying
![]() $\mathsf {reverse\_weight}$
(checking the six cases (R1)–(R6)), those boxes will still be filled with primed entries and so the necessary order relations are respected. Similarly, the boxes directly to the right of the group (if there are any) will be filled with unprimed entries, and any box in row
$\mathsf {reverse\_weight}$
(checking the six cases (R1)–(R6)), those boxes will still be filled with primed entries and so the necessary order relations are respected. Similarly, the boxes directly to the right of the group (if there are any) will be filled with unprimed entries, and any box in row
![]() $i + 1$
will be part of a two-row-group and filled with
$i + 1$
will be part of a two-row-group and filled with
![]() $2$
; after applying
$2$
; after applying
![]() $\mathsf {reverse\_weight}$
, we again have that all order relations are respected. The same holds for the conjugates of these cases after swapping the words ‘row’ with ‘column’, ‘primed’ with ‘unprimed’, ‘below’ with ‘right’, and ‘
$\mathsf {reverse\_weight}$
, we again have that all order relations are respected. The same holds for the conjugates of these cases after swapping the words ‘row’ with ‘column’, ‘primed’ with ‘unprimed’, ‘below’ with ‘right’, and ‘
![]() $(i, i)$
’ with ‘
$(i, i)$
’ with ‘
![]() $(i + 1, i + 1)$
’. This leaves the two mutually conjugate cases
$(i + 1, i + 1)$
’. This leaves the two mutually conjugate cases

Here, we have two possibilities to consider: box
![]() $(i, i + 1)$
is automatically in the same two-row- or two-column-group as one of the other diagonal boxes, but the odd box out could be part of a bar with more than one box. For example, in the tableau
$(i, i + 1)$
is automatically in the same two-row- or two-column-group as one of the other diagonal boxes, but the odd box out could be part of a bar with more than one box. For example, in the tableau  the unprimed bars are part of a two-row-group and the primed bars are part of a two-column-group. If the two diagonal boxes are in different groups, then the three boxes are unchanged by the operation
the unprimed bars are part of a two-row-group and the primed bars are part of a two-column-group. If the two diagonal boxes are in different groups, then the three boxes are unchanged by the operation
![]() $\mathsf {reverse\_weight}$
, all boxes below them (if any) are primed and stay this way after applying
$\mathsf {reverse\_weight}$
, all boxes below them (if any) are primed and stay this way after applying
![]() $\mathsf {reverse\_weight}$
, and all boxes to their right (if any) are unprimed and stay this way after applying
$\mathsf {reverse\_weight}$
, and all boxes to their right (if any) are unprimed and stay this way after applying
![]() $\mathsf {reverse\_weight}$
, so all order relations involving these boxes are preserved. If the two diagonal boxes are part of the same group, and when we apply
$\mathsf {reverse\_weight}$
, so all order relations involving these boxes are preserved. If the two diagonal boxes are part of the same group, and when we apply
![]() $\mathsf {reverse\_weight}$
, we fall into case (R4) or (C4), and the rest of the argument is essentially the same as for the cases discussed above.
$\mathsf {reverse\_weight}$
, we fall into case (R4) or (C4), and the rest of the argument is essentially the same as for the cases discussed above.
3.5 Composing operations
Putting together everything above, we arrive at the main theorem of this section:
Theorem 3.16. The composition
is a shape-preserving and weight-reversing involution of the set of semistandard shifted bar tableaux with all entries in
![]() $\{1',1,2',2\}$
. Moreover, if T is a semistandard shifted bar tableau, then
$\{1',1,2',2\}$
. Moreover, if T is a semistandard shifted bar tableau, then
![]() $\tau ^{\mathrm {ShBT}}(T)$
and T have the same number of primed entries on the main diagonal.
$\tau ^{\mathrm {ShBT}}(T)$
and T have the same number of primed entries on the main diagonal.
Proof. Let T be a semistandard shifted bar tableau. In view of Theorems 3.10 and 3.15, it remains only to prove our claim that
![]() $\tau ^{\mathrm {ShBT}}(T)$
and T have the same number of primed diagonal entries.
$\tau ^{\mathrm {ShBT}}(T)$
and T have the same number of primed diagonal entries.
By considering the various cases in Definition 3.2, we see that the only swaps in the initial application of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}$
that can change a diagonal box are moves of the form
$\mathsf {swap}_{1\leftrightarrow 2'}$
that can change a diagonal box are moves of the form

or its conjugate, where the leftmost (respectively, topmost) affected box belongs to the diagonal. In either case, if such a swap is applied, then it will be the last swap in the computation of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
that changes anything (i.e., any remaining swaps will fall into case (c) of Definition 3.2). Similarly, the only swaps in the final application of
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
that changes anything (i.e., any remaining swaps will fall into case (c) of Definition 3.2). Similarly, the only swaps in the final application of
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
that can change a diagonal box are moves that are the reverse of (3.8) or its conjugate, and when such swaps are applied, they occur as the first swap in the computation when
$\mathsf {unswap}_{1\leftrightarrow 2'}$
that can change a diagonal box are moves that are the reverse of (3.8) or its conjugate, and when such swaps are applied, they occur as the first swap in the computation when
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
is applied to
$\mathsf {unswap}_{1\leftrightarrow 2'}$
is applied to
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
. We now consider exhaustively the possible changes that can occur at the diagonal.
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
. We now consider exhaustively the possible changes that can occur at the diagonal.
First, suppose T contains a single diagonal box
![]() $(i,i)$
, and assume that this box of T is filled with
$(i,i)$
, and assume that this box of T is filled with
![]() $1'$
or
$1'$
or
![]() $2$
. Then
$2$
. Then
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
also possesses a single diagonal box filled with the same entry. In the sorted ShBT
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
also possesses a single diagonal box filled with the same entry. In the sorted ShBT
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, this box belongs either to a one-row- or one-column-group, or to a two-row- or two-column-group that contains exactly one diagonal box. On groups of this type, the operation
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, this box belongs either to a one-row- or one-column-group, or to a two-row- or two-column-group that contains exactly one diagonal box. On groups of this type, the operation
![]() $\mathsf {reverse\_weight}$
preserves the entry in the diagonal box with a unique exception – namely, if the diagonal box belongs to a one-row- or one-column-group whose entries are all equal (as in the last figure in (3.7)).
$\mathsf {reverse\_weight}$
preserves the entry in the diagonal box with a unique exception – namely, if the diagonal box belongs to a one-row- or one-column-group whose entries are all equal (as in the last figure in (3.7)).
In the non-exceptional case,
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
has its unique diagonal box
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
has its unique diagonal box
![]() $(i, i)$
filled with the same value (
$(i, i)$
filled with the same value (
![]() $1'$
or
$1'$
or
![]() $2$
) as T. Applying
$2$
) as T. Applying
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
preserves this property since it only affects boxes containing
$\mathsf {unswap}_{1\leftrightarrow 2'}$
preserves this property since it only affects boxes containing
![]() $1$
and
$1$
and
![]() $2'$
, so
$2'$
, so
![]() $\tau ^{\mathrm {ShBT}}(T)$
also has its diagonal box filled with the same value as T.
$\tau ^{\mathrm {ShBT}}(T)$
also has its diagonal box filled with the same value as T.
Assume we are in the exceptional case, so that the unique diagonal box
![]() $(i, i)$
of
$(i, i)$
of
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is part of a one-row- or one-column-group whose entries are all equal. Without loss of generality (up to conjugation) we can assume that it is a one-row-group whose entries are all
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is part of a one-row- or one-column-group whose entries are all equal. Without loss of generality (up to conjugation) we can assume that it is a one-row-group whose entries are all
![]() $2$
, and so that the diagonal box in
$2$
, and so that the diagonal box in
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
is filled with
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
is filled with
![]() $1$
. Possibly the box
$1$
. Possibly the box
![]() $(i - 1, i)$
directly below the diagonal is empty (i.e., it does not belong to T). Then the very first step of the application of
$(i - 1, i)$
directly below the diagonal is empty (i.e., it does not belong to T). Then the very first step of the application of
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
cannot be a move of the form
$\mathsf {unswap}_{1\leftrightarrow 2'}$
cannot be a move of the form

and hence, the resulting tableau
![]() $\tau ^{\mathrm {ShBT}}(T)$
still has unprimed diagonal entry.
$\tau ^{\mathrm {ShBT}}(T)$
still has unprimed diagonal entry.
If, however, the box
![]() $(i - 1, i)$
is not empty, then in
$(i - 1, i)$
is not empty, then in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
it cannot be filled with
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
it cannot be filled with
![]() $2$
(because
$2$
(because
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is sorted), and it cannot be filled with
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is sorted), and it cannot be filled with
![]() $1$
(because
$1$
(because
![]() $(i, i)$
does not belong to a two-row-group), so it must be filled with a primed entry. Furthermore, we claim that
$(i, i)$
does not belong to a two-row-group), so it must be filled with a primed entry. Furthermore, we claim that
![]() $(i - 1, i)$
cannot be filled with
$(i - 1, i)$
cannot be filled with
![]() $2'$
: if box
$2'$
: if box
![]() $(i-1,i)$
had
$(i-1,i)$
had
![]() $2'$
and the bar of
$2'$
and the bar of
![]() $(i,i)$
had multiple boxes, then
$(i,i)$
had multiple boxes, then
![]() $(i-1,i+1)$
would be filled with
$(i-1,i+1)$
would be filled with
![]() $1$
to be sorted and
$1$
to be sorted and
![]() $(i,i)$
would be in a two-row-group, whereas if box
$(i,i)$
would be in a two-row-group, whereas if box
![]() $(i-1,i)$
had
$(i-1,i)$
had
![]() $2'$
and the bar of
$2'$
and the bar of
![]() $(i,i)$
had just one box, then
$(i,i)$
had just one box, then
![]() $(i-1,i)$
would part of a one-column-group that includes
$(i-1,i)$
would part of a one-column-group that includes
![]() $(i,i)$
, which is a contradiction in either case.
$(i,i)$
, which is a contradiction in either case.
Thus, when the box
![]() $(i - 1, i)$
belongs to T, it must be filled with
$(i - 1, i)$
belongs to T, it must be filled with
![]() $1'$
in
$1'$
in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, and this
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, and this
![]() $1'$
must be part of a two-column group. After applying
$1'$
must be part of a two-column group. After applying
![]() $\mathsf {reverse\_weight}$
to
$\mathsf {reverse\_weight}$
to
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, it follows that the diagonal box will be filled with the value
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, it follows that the diagonal box will be filled with the value
![]() $1$
and the box
$1$
and the box
![]() $(i - 1, i)$
will be filled with
$(i - 1, i)$
will be filled with
![]() $1'$
. This means that applying
$1'$
. This means that applying
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
to
$\mathsf {unswap}_{1\leftrightarrow 2'}$
to
![]() $\mathsf {reverse\_weight}(\mathsf {unswap}_{1\leftrightarrow 2'}(T))$
cannot begin with a move of the form (3.9), and hence, the resulting tableau
$\mathsf {reverse\_weight}(\mathsf {unswap}_{1\leftrightarrow 2'}(T))$
cannot begin with a move of the form (3.9), and hence, the resulting tableau
![]() $\tau ^{\mathrm {ShBT}}(T)$
still has unprimed diagonal entry. This completes the claim in the case that T has one diagonal box and it is filled with
$\tau ^{\mathrm {ShBT}}(T)$
still has unprimed diagonal entry. This completes the claim in the case that T has one diagonal box and it is filled with
![]() $1'$
or
$1'$
or
![]() $2$
.
$2$
.
Continue to assume that T has a single diagonal box
![]() $(i,i)$
, but now suppose this box is filled with
$(i,i)$
, but now suppose this box is filled with
![]() $1$
or
$1$
or
![]() $2'$
. Up to conjugacy, we may assume that the box is filled with
$2'$
. Up to conjugacy, we may assume that the box is filled with
![]() $1$
, so that T looks like
$1$
, so that T looks like

where possibly the bar containing the diagonal box extends to the right. Our objective is to show that the diagonal box
![]() $(i,i)$
is still unprimed in
$(i,i)$
is still unprimed in
![]() $\tau ^{\mathrm {ShBT}}(T)$
. To this end, we first observe that the bar tableau
$\tau ^{\mathrm {ShBT}}(T)$
. To this end, we first observe that the bar tableau
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
must look like
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
must look like

where again ‘the bar of
![]() $1$
s’ may extend to the right. Since
$1$
s’ may extend to the right. Since
![]() $(i, i)$
is the unique diagonal box of T, it must be the case that T does not contain any boxes in row
$(i, i)$
is the unique diagonal box of T, it must be the case that T does not contain any boxes in row
![]() $i + 1$
, and consequently in all four cases ‘the bar of
$i + 1$
, and consequently in all four cases ‘the bar of
![]() $1$
s’ in
$1$
s’ in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is not related by
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is not related by
![]() $\approx $
to any other box. In the second, third and fourth cases of (3.10), it follows that this bar is in a one-row-group; in the first case, it might be part of either a one-row- or one-column-group, depending on the presence and contents of the cells marked ‘
$\approx $
to any other box. In the second, third and fourth cases of (3.10), it follows that this bar is in a one-row-group; in the first case, it might be part of either a one-row- or one-column-group, depending on the presence and contents of the cells marked ‘
![]() $??$
’ in
$??$
’ in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. We consider the cases in order.
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. We consider the cases in order.
In the first case, suppose first that the diagonal box
![]() $(i, i)$
is part of a one-row-group in
$(i, i)$
is part of a one-row-group in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. Then the bar containing
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. Then the bar containing
![]() $(i - 1, i)$
that is filled with
$(i - 1, i)$
that is filled with
![]() $1'$
must belong to a two-column-group in
$1'$
must belong to a two-column-group in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
(or else the two bars would be related by
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
(or else the two bars would be related by
![]() $\sim $
). Therefore, after applying
$\sim $
). Therefore, after applying
![]() $\mathsf {reverse\_weight}$
, the diagonal box in
$\mathsf {reverse\_weight}$
, the diagonal box in
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
will be unprimed and the
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
will be unprimed and the
![]() $(i - 1, i)$
box will still be filled with
$(i - 1, i)$
box will still be filled with
![]() $1'$
. The operation
$1'$
. The operation
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
can only convert an unprimed diagonal box into a primed diagonal box by an application of the operation
$\mathsf {unswap}_{1\leftrightarrow 2'}$
can only convert an unprimed diagonal box into a primed diagonal box by an application of the operation

but this cannot happen when the box
![]() $(i - 1, i)$
is filled with
$(i - 1, i)$
is filled with
![]() $1'$
. Thus, the diagonal box in
$1'$
. Thus, the diagonal box in
![]() $\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
$\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
Continuing with the first case, suppose instead that the diagonal box
![]() $(i, i)$
is part of a one-column-group in
$(i, i)$
is part of a one-column-group in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. Since
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. Since
![]() $(i - 1, i)$
is filled with
$(i - 1, i)$
is filled with
![]() $1'$
in
$1'$
in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, the entire one-column-group is filled with
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
, the entire one-column-group is filled with
![]() $1'$
and
$1'$
and
![]() $1$
. Therefore, after toggling the labels of the group, the diagonal box in
$1$
. Therefore, after toggling the labels of the group, the diagonal box in
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
will be filled with
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
will be filled with
![]() $2$
(and the rest of the one-column-group with
$2$
(and the rest of the one-column-group with
![]() $2'$
). No step in the application of
$2'$
). No step in the application of
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
moves a box filled with
$\mathsf {unswap}_{1\leftrightarrow 2'}$
moves a box filled with
![]() $2$
; hence, the diagonal box in
$2$
; hence, the diagonal box in
![]() $\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
$\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
In the second case, the diagonal box in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
can only belong to a one-row-group, so the diagonal box in
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
can only belong to a one-row-group, so the diagonal box in
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
is unprimed. The operation
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
is unprimed. The operation
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
can only convert an unprimed diagonal box into a primed diagonal box by an application of the operation
$\mathsf {unswap}_{1\leftrightarrow 2'}$
can only convert an unprimed diagonal box into a primed diagonal box by an application of the operation

but this cannot happen when the box
![]() $(i - 1, i)$
is not part of the shape. Thus, the diagonal box in
$(i - 1, i)$
is not part of the shape. Thus, the diagonal box in
![]() $\tau ^{\mathrm {ShBT}}(T)$
is also unprimed in this case.
$\tau ^{\mathrm {ShBT}}(T)$
is also unprimed in this case.
In the third case, the diagonal one-box-bar filled with
![]() $2'$
belongs to the same one-row-group in
$2'$
belongs to the same one-row-group in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
as ‘the bar of
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
as ‘the bar of
![]() $1$
s’. These two bars are filled the same in
$1$
s’. These two bars are filled the same in
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
as in
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
as in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
since when we apply
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
since when we apply
![]() $\mathsf {reverse\_weight}$
, we are in the case of toggling the labels with
$\mathsf {reverse\_weight}$
, we are in the case of toggling the labels with
![]() $p, q> 0$
in the sense of (3.6). Then the very first step of
$p, q> 0$
in the sense of (3.6). Then the very first step of
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
applies the rule
$\mathsf {unswap}_{1\leftrightarrow 2'}$
applies the rule

so the diagonal box in
![]() $\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
$\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
Finally, in the fourth case, we have by sortedness that ‘the bar of
![]() $1$
s’ must be a singleton bar, and the box filled with ‘
$1$
s’ must be a singleton bar, and the box filled with ‘
![]() $??$
’ must actually be filled with
$??$
’ must actually be filled with
![]() $2'$
, so
$2'$
, so
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is of the form
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
is of the form

In this case, the bars containing boxes
![]() $(i - 1, i)$
and
$(i - 1, i)$
and
![]() $(i - 1, i + 1)$
in
$(i - 1, i + 1)$
in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
belong to a two-column-group, and so the one-box bars
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
belong to a two-column-group, and so the one-box bars
![]() $(i, i)$
and
$(i, i)$
and
![]() $(i, i + 1)$
form a one-row-group in
$(i, i + 1)$
form a one-row-group in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. It follows that
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. It follows that
![]() $\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
has the same entries in these four boxes. Then, as in the third case, the very first step of
$\mathsf {reverse\_weight}(\mathsf {swap}_{1\leftrightarrow 2'}(T))$
has the same entries in these four boxes. Then, as in the third case, the very first step of
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
applies the rule
$\mathsf {unswap}_{1\leftrightarrow 2'}$
applies the rule

and so the diagonal box in
![]() $\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
$\tau ^{\mathrm {ShBT}}(T)$
is unprimed in this case.
Finally, we consider the case when T has two diagonal boxes. If both diagonal boxes are unprimed, then there are three ways that they and the box between them can be filled in T:

After applying
![]() $\mathsf {swap}_{1\leftrightarrow 2'}$
to such a tableau, we might end up with one of the near-diagonal arrangements
$\mathsf {swap}_{1\leftrightarrow 2'}$
to such a tableau, we might end up with one of the near-diagonal arrangements

where in the last case, necessarily the diagonal box  forms a one-box bar (following a move of the form (3.8)). In the first case, applying
forms a one-box bar (following a move of the form (3.8)). In the first case, applying
![]() $\mathsf {reverse\_weight}$
toggles the bar divisions and so does not change the contents of the diagonal boxes or the box
$\mathsf {reverse\_weight}$
toggles the bar divisions and so does not change the contents of the diagonal boxes or the box
![]() $(i, i + 1)$
, and applying
$(i, i + 1)$
, and applying
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
to the result preserves the diagonal boxes. The second and third cases are precisely those to which the rule (R1) in the definition of
$\mathsf {unswap}_{1\leftrightarrow 2'}$
to the result preserves the diagonal boxes. The second and third cases are precisely those to which the rule (R1) in the definition of
![]() $\mathsf {reverse\_weight}$
applies; they are interchanged, and then
$\mathsf {reverse\_weight}$
applies; they are interchanged, and then
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
restores the unprimed diagonal boxes.
$\mathsf {unswap}_{1\leftrightarrow 2'}$
restores the unprimed diagonal boxes.
The argument when both diagonal boxes of T are primed is precisely the conjugate of the previous case. This leaves the situation when T has exactly two diagonal boxes, only one of which is primed. Then there are six possible arrangements for the two diagonal boxes and the box between them, in three conjugate pairs:

Suppose T belongs to one of the first two cases. Then
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
still has the near-diagonal arrangement
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
still has the near-diagonal arrangement  or
or  (possibly reversed from what it had before); up to conjugacy, we assume the former. If the diagonal boxes
(possibly reversed from what it had before); up to conjugacy, we assume the former. If the diagonal boxes
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
belong to different groups, then after applying
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
belong to different groups, then after applying
![]() $\mathsf {reverse\_weight}$
, the near-diagonal arrangement is unchanged, and then
$\mathsf {reverse\_weight}$
, the near-diagonal arrangement is unchanged, and then
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
does not affect the diagonal boxes. Suppose instead that the two diagonal boxes belong to the same group in
$\mathsf {unswap}_{1\leftrightarrow 2'}$
does not affect the diagonal boxes. Suppose instead that the two diagonal boxes belong to the same group in
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. Depending on whether the bars containing boxes
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
. Depending on whether the bars containing boxes
![]() $(i, i + 1)$
and
$(i, i + 1)$
and
![]() $(i + 1, i + 1)$
extend to the right, applying
$(i + 1, i + 1)$
extend to the right, applying
![]() $\mathsf {reverse\_weight}$
to
$\mathsf {reverse\_weight}$
to
![]() $\mathsf {swap}_{1\leftrightarrow 2'}(T)$
belongs to either case (R2) or (R4), and the image necessarily has the near-diagonal arrangement
$\mathsf {swap}_{1\leftrightarrow 2'}(T)$
belongs to either case (R2) or (R4), and the image necessarily has the near-diagonal arrangement

Applying
![]() $\mathsf {unswap}_{1\leftrightarrow 2'}$
to such a tableau results in a tableau with near-diagonal arrangement
$\mathsf {unswap}_{1\leftrightarrow 2'}$
to such a tableau results in a tableau with near-diagonal arrangement

and so we conclude that
![]() $\tau ^{\mathrm {ShBT}}(T)$
has exactly one primed diagonal box, as needed.
$\tau ^{\mathrm {ShBT}}(T)$
has exactly one primed diagonal box, as needed.
The remaining four cases are, up to conjugacy, precisely the reverse direction of the cases just considered; since
![]() $\tau ^{\mathrm {ShBT}}$
is an involution, it follows that its action in these cases also preserves the number of primed diagonal boxes. This completes the proof.
$\tau ^{\mathrm {ShBT}}$
is an involution, it follows that its action in these cases also preserves the number of primed diagonal boxes. This completes the proof.
4 Generating function derivations
Let
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
be strict partitions, and recall the definitions of the sets of shifted plane partitions
$\lambda $
be strict partitions, and recall the definitions of the sets of shifted plane partitions
![]() $ \mathsf {ShPP}_P(\lambda /\mu ) \subseteq \mathsf {ShPP}_Q(\lambda /\mu )$
and semistandard shifted bar tableaux
$ \mathsf {ShPP}_P(\lambda /\mu ) \subseteq \mathsf {ShPP}_Q(\lambda /\mu )$
and semistandard shifted bar tableaux
![]() $\mathsf {ShBT}_P(\lambda /\mu ) \subseteq \mathsf {ShBT}_Q(\lambda /\mu )$
from Section 2.2. Throughout this section, we work with the concrete generating functions
$\mathsf {ShBT}_P(\lambda /\mu ) \subseteq \mathsf {ShBT}_Q(\lambda /\mu )$
from Section 2.2. Throughout this section, we work with the concrete generating functions
 $$\begin{align*}\begin{aligned} g\hspace{-0.1mm}p^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in {\mathsf{ShPP}_P(\lambda/\mu)}} (-\beta)^{|\lambda/\mu| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{ x}^{\operatorname{wt}_{\mathrm{PP}(T)}} ,\\ g\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in {\mathsf{ShPP}_Q(\lambda/\mu)}} (-\beta)^{|\lambda/\mu| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{ x}^{\operatorname{wt}_{\mathrm{PP}(T)}}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} g\hspace{-0.1mm}p^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in {\mathsf{ShPP}_P(\lambda/\mu)}} (-\beta)^{|\lambda/\mu| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{ x}^{\operatorname{wt}_{\mathrm{PP}(T)}} ,\\ g\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in {\mathsf{ShPP}_Q(\lambda/\mu)}} (-\beta)^{|\lambda/\mu| - |\operatorname{wt}_{\mathrm{PP}(T)|}} \mathbf{ x}^{\operatorname{wt}_{\mathrm{PP}(T)}}, \end{aligned} \end{align*}$$
and
 $$\begin{align*}\begin{aligned} j\hspace{-0.1mm}p^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in \mathsf{ShBT}_P(\lambda/\mu)} (-\beta)^{|\lambda/\mu|-|T|} \mathbf{x}^{T} ,\\ j\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in \mathsf{ShBT}_Q(\lambda/\mu)} (-\beta)^{|\lambda/\mu| -|T|} \mathbf{x}^{T}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} j\hspace{-0.1mm}p^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in \mathsf{ShBT}_P(\lambda/\mu)} (-\beta)^{|\lambda/\mu|-|T|} \mathbf{x}^{T} ,\\ j\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu} &:= \sum_{T\in \mathsf{ShBT}_Q(\lambda/\mu)} (-\beta)^{|\lambda/\mu| -|T|} \mathbf{x}^{T}. \end{aligned} \end{align*}$$
Our goal is to prove that these power series coincide with the symmetric functions
![]() $g\hspace {-0.1mm}p_{\lambda /\mu }$
,
$g\hspace {-0.1mm}p_{\lambda /\mu }$
,
![]() $g\hspace {-0.1mm}q_{\lambda /\mu }$
,
$g\hspace {-0.1mm}q_{\lambda /\mu }$
,
![]() $j\hspace {-0.1mm}p_{\lambda /\mu }$
, and
$j\hspace {-0.1mm}p_{\lambda /\mu }$
, and
![]() $j\hspace {-0.1mm}q_{\lambda /\mu }$
defined in Section 2.2. On setting
$j\hspace {-0.1mm}q_{\lambda /\mu }$
defined in Section 2.2. On setting
![]() $\mu =\emptyset $
, this will establish Theorems 1.4 and 1.5.
$\mu =\emptyset $
, this will establish Theorems 1.4 and 1.5.
4.1 Base cases and symmetry
Our proof strategy uses an inductive algebraic argument whose base case is the following:
Proposition 4.1 [Reference Chiu and Marberg4, Prop. 7.5]; [Reference Nakagawa and Naruse19, Prop. 5.2].
If
![]() $\lambda $
has at most one part, then
$\lambda $
has at most one part, then
Our inductive step relies on the following consequence of Theorem 3.16:
Theorem 4.2. The power series
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
and
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
are symmetric in the
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
are symmetric in the
![]() $x_i$
variables.
$x_i$
variables.
Proof. The weight of a general ShBT is the tuple
![]() $a=(a_1,a_2,\dots )$
, where
$a=(a_1,a_2,\dots )$
, where
![]() $a_i$
is the number of bars that contain either i or
$a_i$
is the number of bars that contain either i or
![]() $i'$
. Let
$i'$
. Let
![]() $|a| = a_1+a_2+\dots $
. The coefficient of
$|a| = a_1+a_2+\dots $
. The coefficient of
![]() $(-\beta )^{|\lambda /\mu |-|a|} x_1^{a_1} \cdots x_i^{a_i} x_{i + 1}^{a_{i + 1}} \cdots $
in
$(-\beta )^{|\lambda /\mu |-|a|} x_1^{a_1} \cdots x_i^{a_i} x_{i + 1}^{a_{i + 1}} \cdots $
in
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
is the number of semistandard ShBT’s of shape
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
is the number of semistandard ShBT’s of shape
![]() $\lambda /\mu $
with weight
$\lambda /\mu $
with weight
![]() $a=(a_1,a_2,\dots )$
. By the first part of Theorem 3.16, applying the map
$a=(a_1,a_2,\dots )$
. By the first part of Theorem 3.16, applying the map
![]() $\tau ^{\mathrm {ShBT}}$
to the subtableaux generated by the entries
$\tau ^{\mathrm {ShBT}}$
to the subtableaux generated by the entries
![]() $i', i, i' + 1, i + 1$
gives a bijection with the ShBT’s counted by the coefficient of
$i', i, i' + 1, i + 1$
gives a bijection with the ShBT’s counted by the coefficient of
![]() $(-\beta )^{|\lambda /\mu |-|a|} x_1^{a_1} \cdots x_i^{a_{i + 1}} x_{i + 1}^{a_{i}} \cdots $
. Since any finitely supported permutation is a product of adjacent transpositions, it follows that
$(-\beta )^{|\lambda /\mu |-|a|} x_1^{a_1} \cdots x_i^{a_{i + 1}} x_{i + 1}^{a_{i}} \cdots $
. Since any finitely supported permutation is a product of adjacent transpositions, it follows that
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
is symmetric in the
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
is symmetric in the
![]() $x_i$
variables.
$x_i$
variables.
The second part of Theorem 3.16 ensures that the map
![]() $\tau ^{\mathrm {ShBT}}$
restricts to an involution on the subset
$\tau ^{\mathrm {ShBT}}$
restricts to an involution on the subset
![]() $\mathsf {ShBT}_P(\lambda /\mu )\subseteq \mathsf {ShBT}_Q(\lambda /\mu )$
consisting of those ShBT’s with no primed diagonal entries. Thus,
$\mathsf {ShBT}_P(\lambda /\mu )\subseteq \mathsf {ShBT}_Q(\lambda /\mu )$
consisting of those ShBT’s with no primed diagonal entries. Thus,
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
is symmetric by the same argument.
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
is symmetric by the same argument.
In the next three subsections, we derive a Pieri rule for the
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}$
- and
$j\hspace {-0.1mm}p^{\mathrm {comb}}$
- and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}$
-functions, in order to prove that
$j\hspace {-0.1mm}q^{\mathrm {comb}}$
-functions, in order to prove that
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }=j\hspace {-0.1mm}p_{\lambda /\mu }$
and
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }=j\hspace {-0.1mm}p_{\lambda /\mu }$
and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }=j\hspace {-0.1mm}q_{\lambda /\mu }$
. We then use these results to derive the analogous identities for
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }=j\hspace {-0.1mm}q_{\lambda /\mu }$
. We then use these results to derive the analogous identities for
![]() $g\hspace {-0.1mm}p_{\lambda /\mu }$
and
$g\hspace {-0.1mm}p_{\lambda /\mu }$
and
![]() $g\hspace {-0.1mm}q_{\lambda /\mu }$
by a formal argument in Section 4.5.
$g\hspace {-0.1mm}q_{\lambda /\mu }$
by a formal argument in Section 4.5.
4.2 Product formulas and one-row identities
There is an easy way to express
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }j\hspace {-0.1mm}q^{\mathrm {comb}}_{\nu /\kappa }$
and
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }j\hspace {-0.1mm}q^{\mathrm {comb}}_{\nu /\kappa }$
and
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }j\hspace {-0.1mm}q^{\mathrm {comb}}_{\nu /\kappa } $
as sums of other functions indexed by skew shapes. Suppose
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }j\hspace {-0.1mm}q^{\mathrm {comb}}_{\nu /\kappa } $
as sums of other functions indexed by skew shapes. Suppose
![]() $\rho $
and
$\rho $
and
![]() $\tau $
are finite, nonempty subsets of
$\tau $
are finite, nonempty subsets of
![]() $\{1,2,3,\dots \}\times \{1,2,3,\dots \}$
. Let
$\{1,2,3,\dots \}\times \{1,2,3,\dots \}$
. Let
In French notation,
![]() $(i, j)$
is the box of
$(i, j)$
is the box of
![]() $\rho $
in its bottom row that is farthest to the right. Then let
$\rho $
in its bottom row that is farthest to the right. Then let
In French notation,
![]() $(k, l)$
is the box of
$(k, l)$
is the box of
![]() $\tau $
in its top row that is farthest to the left. Form a new diagram
$\tau $
in its top row that is farthest to the left. Form a new diagram
![]() $ \rho \vartriangleright \tau $
by translating the sets
$ \rho \vartriangleright \tau $
by translating the sets
![]() $\rho $
and
$\rho $
and
![]() $\tau $
so that
$\tau $
so that
![]() $(i,j)$
is directly to the left of
$(i,j)$
is directly to the left of
![]() $(k,l)$
in the same row; form
$(k,l)$
in the same row; form
![]() $ \rho \vartriangleleft \tau $
by translating the two sets so that
$ \rho \vartriangleleft \tau $
by translating the two sets so that
![]() $(i,j)$
is directly above
$(i,j)$
is directly above
![]() $(k,l)$
in the same column; and form
$(k,l)$
in the same column; and form
![]() $ \rho \circ \tau $
by translating the two sets so that the boxes
$ \rho \circ \tau $
by translating the two sets so that the boxes
![]() $(i,j)$
are
$(i,j)$
are
![]() $(k,l)$
coincide. If
$(k,l)$
coincide. If
then these shapes are defined precisely by setting
 $$\begin{align*}\begin{aligned} \rho \vartriangleright \tau &:= \Bigl[ \rho + ( \Delta_1 ,\Delta_1) \Bigr]\sqcup \Bigl[ \tau + (0,\Delta_2)\Bigr], \\ \rho \vartriangleleft \tau &:=\Bigl[ \rho + ( \Delta_1+1 ,\Delta_1+1) \Bigr]\sqcup \Bigl[ \tau + (0,\Delta_2)\Bigr], \\ \rho \circ \tau &:= \Bigl[ \rho + ( \Delta_1 ,\Delta_1) \Bigr] \cup \Bigl[ \tau + (0,\Delta_2-1)\Bigr]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \rho \vartriangleright \tau &:= \Bigl[ \rho + ( \Delta_1 ,\Delta_1) \Bigr]\sqcup \Bigl[ \tau + (0,\Delta_2)\Bigr], \\ \rho \vartriangleleft \tau &:=\Bigl[ \rho + ( \Delta_1+1 ,\Delta_1+1) \Bigr]\sqcup \Bigl[ \tau + (0,\Delta_2)\Bigr], \\ \rho \circ \tau &:= \Bigl[ \rho + ( \Delta_1 ,\Delta_1) \Bigr] \cup \Bigl[ \tau + (0,\Delta_2-1)\Bigr]. \end{aligned} \end{align*}$$
The third union is not disjoint. All three shapes have the same number of diagonal boxes as
![]() $\rho $
.
$\rho $
.
Example 4.3. If our two shapes are
then we have
![]() $(i,j) = (1,3)$
and
$(i,j) = (1,3)$
and
![]() $(k,l) = (2,1)$
, so
$(k,l) = (2,1)$
, so
![]() $\Delta _1 = 1$
and
$\Delta _1 = 1$
and
![]() $\Delta _2 = 4$
. Thus,
$\Delta _2 = 4$
. Thus,

Suppose
![]() $\rho = \textsf {SD}_{\lambda /\mu }$
for strict partitions
$\rho = \textsf {SD}_{\lambda /\mu }$
for strict partitions
![]() $\mu \subsetneq \lambda $
and
$\mu \subsetneq \lambda $
and
![]() $\tau = \textsf {D}_{\nu /\kappa }$
for arbitrary partitions
$\tau = \textsf {D}_{\nu /\kappa }$
for arbitrary partitions
![]() $\kappa \subsetneq \nu $
. We may view
$\kappa \subsetneq \nu $
. We may view
![]() $\tau = \textsf {D}_{\nu /\kappa }$
as a translation of a shifted skew shape: if
$\tau = \textsf {D}_{\nu /\kappa }$
as a translation of a shifted skew shape: if
![]() $m:=\ell (\nu )-1$
and
$m:=\ell (\nu )-1$
and
![]() $\delta :=(m,\dots ,1,0)$
, then
$\delta :=(m,\dots ,1,0)$
, then
![]() $\tau $
is the tableau formed by translating
$\tau $
is the tableau formed by translating
![]() $\textsf {SD}_{(\nu +\delta )/(\kappa +\delta )}$
to the left by m columns. In this case, we define
$\textsf {SD}_{(\nu +\delta )/(\kappa +\delta )}$
to the left by m columns. In this case, we define
![]() $\mathsf {ShBT}_Q(\tau ) := \mathsf {ShBT}_Q((\nu +\delta )/(\kappa +\delta ))$
and
$\mathsf {ShBT}_Q(\tau ) := \mathsf {ShBT}_Q((\nu +\delta )/(\kappa +\delta ))$
and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\tau } := j\hspace {-0.1mm}q^{\mathrm {comb}}_{(\nu +\delta )/(\kappa +\delta )}$
.
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\tau } := j\hspace {-0.1mm}q^{\mathrm {comb}}_{(\nu +\delta )/(\kappa +\delta )}$
.
Proposition 4.4. Suppose
![]() $\rho $
is a nonempty shifted skew shape and
$\rho $
is a nonempty shifted skew shape and
![]() $\tau $
is a nonempty unshifted skew shape, as above. Then
$\tau $
is a nonempty unshifted skew shape, as above. Then
![]() $ \rho \vartriangleright \tau $
,
$ \rho \vartriangleright \tau $
,
![]() $ \rho \vartriangleleft \tau $
, and
$ \rho \vartriangleleft \tau $
, and
![]() $ \rho \circ \tau $
are shifted skew shapes, and it holds that
$ \rho \circ \tau $
are shifted skew shapes, and it holds that
 $$\begin{align*}\begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho}j\hspace{-0.1mm}q^{\mathrm{comb}}_\tau &= j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho \vartriangleright \tau} + j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho \vartriangleleft \tau} + \beta j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho \circ \tau}, \\ j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho}j\hspace{-0.1mm}q^{\mathrm{comb}}_\tau &= j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho \vartriangleright \tau} + j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho \vartriangleleft \tau} + \beta j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho \circ \tau}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho}j\hspace{-0.1mm}q^{\mathrm{comb}}_\tau &= j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho \vartriangleright \tau} + j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho \vartriangleleft \tau} + \beta j\hspace{-0.1mm}q^{\mathrm{comb}}_{\rho \circ \tau}, \\ j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho}j\hspace{-0.1mm}q^{\mathrm{comb}}_\tau &= j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho \vartriangleright \tau} + j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho \vartriangleleft \tau} + \beta j\hspace{-0.1mm}p^{\mathrm{comb}}_{\rho \circ \tau}. \end{aligned}\end{align*}$$
Proof. The following argument is similar to the proof of [Reference Lam and Pylyavskyy11, Lem. 9.12]. Checking that
![]() $ \rho \vartriangleright \tau $
,
$ \rho \vartriangleright \tau $
,
![]() $ \rho \vartriangleleft \tau $
and
$ \rho \vartriangleleft \tau $
and
![]() $ \rho \circ \tau $
are shifted skew shapes is straightforward. Suppose
$ \rho \circ \tau $
are shifted skew shapes is straightforward. Suppose
![]() $T \in \mathsf {ShBT}_Q(\rho )$
and
$T \in \mathsf {ShBT}_Q(\rho )$
and
![]() $U \in \mathsf {ShBT}_Q(\tau )$
. Let
$U \in \mathsf {ShBT}_Q(\tau )$
. Let
![]() $T \vartriangleright U $
and
$T \vartriangleright U $
and
![]() $T \vartriangleleft U$
be the shifted bar tableaux of shapes
$T \vartriangleleft U$
be the shifted bar tableaux of shapes
![]() $\rho \vartriangleright \tau $
and
$\rho \vartriangleright \tau $
and
![]() $\rho \vartriangleleft \tau $
given by translating the boxes of T and U in the obvious way.
$\rho \vartriangleleft \tau $
given by translating the boxes of T and U in the obvious way.
If
![]() $T_{ij} < U_{kl}$
or
$T_{ij} < U_{kl}$
or
![]() $T_{ij} = U_{kl}\in \mathbb {Z}$
, then we have
$T_{ij} = U_{kl}\in \mathbb {Z}$
, then we have
![]() $T \vartriangleright U \in \mathsf {ShBT}_Q(\rho \vartriangleright \tau )$
,
$T \vartriangleright U \in \mathsf {ShBT}_Q(\rho \vartriangleright \tau )$
,
![]() $|T \vartriangleright U| = |T|+|U|$
, and
$|T \vartriangleright U| = |T|+|U|$
, and
![]() $x^{T \vartriangleright U} = x^T x^U$
. However, if
$x^{T \vartriangleright U} = x^T x^U$
. However, if
![]() $T_{ij}> U_{kl}$
or
$T_{ij}> U_{kl}$
or
![]() $T_{ij} = U_{kl}\in \mathbb {Z}'$
, then it holds that
$T_{ij} = U_{kl}\in \mathbb {Z}'$
, then it holds that
![]() $T \vartriangleleft U \in \mathsf {ShBT}_Q(\rho \vartriangleleft \tau )$
,
$T \vartriangleleft U \in \mathsf {ShBT}_Q(\rho \vartriangleleft \tau )$
,
![]() $|T \vartriangleleft U| = |T|+|U|$
and
$|T \vartriangleleft U| = |T|+|U|$
and
![]() $x^{T \vartriangleleft U} = x^T x^U$
.
$x^{T \vartriangleleft U} = x^T x^U$
.
Merging the boxes of
![]() $\rho \vartriangleright \tau $
or
$\rho \vartriangleright \tau $
or
![]() $\rho \vartriangleleft \tau $
corresponding to
$\rho \vartriangleleft \tau $
corresponding to
![]() $(i,j) \in \rho $
and
$(i,j) \in \rho $
and
![]() $(k,l) \in \tau $
gives a bijection from the set of elements in
$(k,l) \in \tau $
gives a bijection from the set of elements in
![]() $ \mathsf {ShBT}_Q(\rho \vartriangleright \tau )\sqcup \mathsf {ShBT}_Q(\rho \vartriangleleft \tau )$
that do not arise from one of these cases (namely, those in which the boxes that are adjacent but of different colors in Example 4.3 belong to the same bar) to
$ \mathsf {ShBT}_Q(\rho \vartriangleright \tau )\sqcup \mathsf {ShBT}_Q(\rho \vartriangleleft \tau )$
that do not arise from one of these cases (namely, those in which the boxes that are adjacent but of different colors in Example 4.3 belong to the same bar) to
![]() $ \mathsf {ShBT}_Q(\rho \circ \tau )$
. The expansion for
$ \mathsf {ShBT}_Q(\rho \circ \tau )$
. The expansion for
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\rho }j\hspace {-0.1mm}q^{\mathrm {comb}}_\tau $
then follows. Under these bijections, the diagonal boxes in
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\rho }j\hspace {-0.1mm}q^{\mathrm {comb}}_\tau $
then follows. Under these bijections, the diagonal boxes in
![]() $T \vartriangleleft U$
and
$T \vartriangleleft U$
and
![]() $T \vartriangleright U$
are filled with the same entries as the diagonal boxes in T, so the formula for
$T \vartriangleright U$
are filled with the same entries as the diagonal boxes in T, so the formula for
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\rho }j\hspace {-0.1mm}q^{\mathrm {comb}}_\tau $
also follows.
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\rho }j\hspace {-0.1mm}q^{\mathrm {comb}}_\tau $
also follows.
Let
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_n := j\hspace {-0.1mm}p^{\mathrm {comb}}_{(n)}$
and
$j\hspace {-0.1mm}p^{\mathrm {comb}}_n := j\hspace {-0.1mm}p^{\mathrm {comb}}_{(n)}$
and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_n := j\hspace {-0.1mm}q^{\mathrm {comb}}_{(n)}$
for
$j\hspace {-0.1mm}q^{\mathrm {comb}}_n := j\hspace {-0.1mm}q^{\mathrm {comb}}_{(n)}$
for
![]() $n>0$
and
$n>0$
and
![]() $ j\hspace {-0.1mm}p^{\mathrm {comb}}_0 = j\hspace {-0.1mm}q^{\mathrm {comb}}_0 := 1$
.
$ j\hspace {-0.1mm}p^{\mathrm {comb}}_0 = j\hspace {-0.1mm}q^{\mathrm {comb}}_0 := 1$
.
Corollary 4.5. Suppose
![]() $\lambda $
is a nonempty strict partition and
$\lambda $
is a nonempty strict partition and
![]() $n\in \mathbb {Z}_{>0}$
. Then
$n\in \mathbb {Z}_{>0}$
. Then
 $$\begin{align*}\begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_\lambda j\hspace{-0.1mm}q^{\mathrm{comb}}_n &= j\hspace{-0.1mm}q^{\mathrm{comb}}_{(n+\lambda_1,\lambda_2,\lambda_3,\dots)} +\beta j\hspace{-0.1mm}q^{\mathrm{comb}}_{(n+\lambda_1-1,\lambda_2,\lambda_3,\dots)} + j\hspace{-0.1mm}q^{\mathrm{comb}}_{(n+\lambda_1,\lambda_1,\lambda_2,\dots)/(\lambda_1)}, \\ j\hspace{-0.1mm}p^{\mathrm{comb}}_\lambda j\hspace{-0.1mm}q^{\mathrm{comb}}_n &= j\hspace{-0.1mm}p^{\mathrm{comb}}_{(n+\lambda_1,\lambda_2,\lambda_3,\dots)} +\beta j\hspace{-0.1mm}p^{\mathrm{comb}}_{(n+\lambda_1-1,\lambda_2,\lambda_3,\dots)} + j\hspace{-0.1mm}p^{\mathrm{comb}}_{(n+\lambda_1,\lambda_1,\lambda_2,\dots)/(\lambda_1)}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_\lambda j\hspace{-0.1mm}q^{\mathrm{comb}}_n &= j\hspace{-0.1mm}q^{\mathrm{comb}}_{(n+\lambda_1,\lambda_2,\lambda_3,\dots)} +\beta j\hspace{-0.1mm}q^{\mathrm{comb}}_{(n+\lambda_1-1,\lambda_2,\lambda_3,\dots)} + j\hspace{-0.1mm}q^{\mathrm{comb}}_{(n+\lambda_1,\lambda_1,\lambda_2,\dots)/(\lambda_1)}, \\ j\hspace{-0.1mm}p^{\mathrm{comb}}_\lambda j\hspace{-0.1mm}q^{\mathrm{comb}}_n &= j\hspace{-0.1mm}p^{\mathrm{comb}}_{(n+\lambda_1,\lambda_2,\lambda_3,\dots)} +\beta j\hspace{-0.1mm}p^{\mathrm{comb}}_{(n+\lambda_1-1,\lambda_2,\lambda_3,\dots)} + j\hspace{-0.1mm}p^{\mathrm{comb}}_{(n+\lambda_1,\lambda_1,\lambda_2,\dots)/(\lambda_1)}. \end{aligned} \end{align*}$$
Proof. Take
![]() $\rho = \textsf {SD}_\lambda $
and
$\rho = \textsf {SD}_\lambda $
and
![]() $\tau = \textsf {D}_{(n)}$
in Proposition 4.4.
$\tau = \textsf {D}_{(n)}$
in Proposition 4.4.
Given ![]() , form
, form ![]() by setting
by setting
![]() $x_1= t$
and
$x_1= t$
and
![]() $x_i = 0$
for all
$x_i = 0$
for all
![]() $i>0$
.
$i>0$
.
Proposition 4.6. One has
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_1(t) = t$
and
$j\hspace {-0.1mm}p^{\mathrm {comb}}_1(t) = t$
and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_1(t) = 2t$
, and if
$j\hspace {-0.1mm}q^{\mathrm {comb}}_1(t) = 2t$
, and if
![]() $n\geq 2$
, then
$n\geq 2$
, then
Proof. These identities are straightforward to check from the definitions.
4.3 Bar tableau generating functions with diagonal primes
Let
![]() $\Lambda = (\Lambda _1,\Lambda _2,\Lambda _3,\dots )$
be a strict partition, and define
$\Lambda = (\Lambda _1,\Lambda _2,\Lambda _3,\dots )$
be a strict partition, and define
![]() $\Gamma = (\Lambda _2,\Lambda _3,\dots )$
. Then
$\Gamma = (\Lambda _2,\Lambda _3,\dots )$
. Then
![]() $\textsf {SD}_{\Lambda /\nu }$
is a (not necessarily connected) shifted ribbon if and only if
$\textsf {SD}_{\Lambda /\nu }$
is a (not necessarily connected) shifted ribbon if and only if
![]() $\nu $
contains
$\nu $
contains
![]() $\Gamma $
and is contained in
$\Gamma $
and is contained in
![]() $\Lambda $
. We fix one such strict partition
$\Lambda $
. We fix one such strict partition
![]() $\Psi = (\Psi _1,\Psi _2,\dots )$
with
$\Psi = (\Psi _1,\Psi _2,\dots )$
with
![]() $\Gamma \subseteq \Psi \subseteq \Lambda $
. Throughout this subsection, the capitalized Greek letters
$\Gamma \subseteq \Psi \subseteq \Lambda $
. Throughout this subsection, the capitalized Greek letters
![]() $\Lambda $
,
$\Lambda $
,
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Psi $
will denote these fixed partitions, and we will use the typical lower case symbols
$\Psi $
will denote these fixed partitions, and we will use the typical lower case symbols
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
,
$\mu $
,
![]() $\nu $
, etc., for partitions that may be arbitrary.
$\nu $
, etc., for partitions that may be arbitrary.
Define a forced box in
![]() $ \textsf {SD}_{\Lambda /\Psi }$
to be a position
$ \textsf {SD}_{\Lambda /\Psi }$
to be a position
![]() $(i,j) $
such that
$(i,j) $
such that
![]() $(i+1,j),(i+1,j-1) \in \textsf {SD}_{\Lambda /\Psi }$
or
$(i+1,j),(i+1,j-1) \in \textsf {SD}_{\Lambda /\Psi }$
or
![]() $(i,j-1),(i+1,j-1) \in \textsf {SD}_{\Lambda /\Psi }$
. These are the boxes containing
$(i,j-1),(i+1,j-1) \in \textsf {SD}_{\Lambda /\Psi }$
. These are the boxes containing
![]() $\bullet $
in
$\bullet $
in ![]() and
and ![]() . For this subsection, we also fix the meaning of certain integer parameters
. For this subsection, we also fix the meaning of certain integer parameters
![]() $\mathsf {sc}$
,
$\mathsf {sc}$
,
![]() $\mathsf {mc}$
,
$\mathsf {mc}$
,
![]() $\mathsf {fb}$
,
$\mathsf {fb}$
,
![]() $\mathsf {res}$
. Let
$\mathsf {res}$
. Let
![]() $\mathsf {sc}$
be the number of singleton connected components in
$\mathsf {sc}$
be the number of singleton connected components in
![]() $\textsf {SD}_{\Lambda /\Psi }$
(i.e., components with only one box), let
$\textsf {SD}_{\Lambda /\Psi }$
(i.e., components with only one box), let
![]() $\mathsf {mc}$
be the number of multiple box connected components, let
$\mathsf {mc}$
be the number of multiple box connected components, let
![]() $\mathsf {fb}$
be the number of forced boxes in
$\mathsf {fb}$
be the number of forced boxes in
![]() $\textsf {SD}_{\Lambda /\Psi }$
, and let
$\textsf {SD}_{\Lambda /\Psi }$
, and let
![]() $\mathsf {res} = |\Lambda | - |\Psi | - \mathsf {sc} - 2\mathsf {mc}-\mathsf {fb}+2$
be a residual value. We always have
$\mathsf {res} = |\Lambda | - |\Psi | - \mathsf {sc} - 2\mathsf {mc}-\mathsf {fb}+2$
be a residual value. We always have
![]() $\mathsf {res}\geq 2$
.
$\mathsf {res}\geq 2$
.
Lemma 4.7. We have
![]() $ j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t) = (2t^2 -\beta t) (t-\beta )^{\mathsf {res}-2} 2^{\mathsf {sc}} t^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2t -\beta )^{\mathsf {mc}-1} $
.
$ j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t) = (2t^2 -\beta t) (t-\beta )^{\mathsf {res}-2} 2^{\mathsf {sc}} t^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2t -\beta )^{\mathsf {mc}-1} $
.
Proof. Consider the tableaux in
![]() $\mathsf {ShBT}_Q(\Lambda /\Psi )$
with all entries in
$\mathsf {ShBT}_Q(\Lambda /\Psi )$
with all entries in
![]() $\{1' ,1\}$
, with boxes ordered in the usual row-reading order. The first entry in each connected component may be arbitrarily primed or unprimed, while the entries in all other boxes (ignoring bars) are uniquely determined by the shape. In each connected component, the first box must be the beginning of a new bar, as must every forced box (if any are present). In a connected component with multiple boxes, if the first two boxes are in the same row (respectively, column), then the second box is only required to start a new bar if the first box is primed (respectively, unprimed). Any boxes not included in these cases may either start a new bar or continue the bar of its predecessor. Comparing these observations with the definition
$\{1' ,1\}$
, with boxes ordered in the usual row-reading order. The first entry in each connected component may be arbitrarily primed or unprimed, while the entries in all other boxes (ignoring bars) are uniquely determined by the shape. In each connected component, the first box must be the beginning of a new bar, as must every forced box (if any are present). In a connected component with multiple boxes, if the first two boxes are in the same row (respectively, column), then the second box is only required to start a new bar if the first box is primed (respectively, unprimed). Any boxes not included in these cases may either start a new bar or continue the bar of its predecessor. Comparing these observations with the definition
![]() $ j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }$
, we conclude that
$ j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }$
, we conclude that
![]() $ j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t) = (2t)^{\mathsf {sc}} (t^2 + t(t-\beta ))^{\mathsf {mc}} t^{\mathsf {fb}} (t-\beta )^{|\Lambda |-|\Psi | - 2 \mathsf {sc}-\mathsf {mc}-\mathsf {fb}}$
, which gives the result after rearranging terms.
$ j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t) = (2t)^{\mathsf {sc}} (t^2 + t(t-\beta ))^{\mathsf {mc}} t^{\mathsf {fb}} (t-\beta )^{|\Lambda |-|\Psi | - 2 \mathsf {sc}-\mathsf {mc}-\mathsf {fb}}$
, which gives the result after rearranging terms.
The set of polynomials
![]() $\{j\hspace {-0.1mm}q^{\mathrm {comb}}_n(t): n\geq 0\}$
is a homogeneous
$\{j\hspace {-0.1mm}q^{\mathrm {comb}}_n(t): n\geq 0\}$
is a homogeneous
![]() $\mathbb {Q}[\beta ]$
-basis for
$\mathbb {Q}[\beta ]$
-basis for
![]() $\mathbb {Q}[\beta ,t]$
by Proposition 4.6, and so
$\mathbb {Q}[\beta ,t]$
by Proposition 4.6, and so
for a unique choice of numbers
![]() $ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} \in \mathbb {Q}$
. Recall that
$ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} \in \mathbb {Q}$
. Recall that
![]() $\Psi $
is a strict partition with
$\Psi $
is a strict partition with
![]() $\Gamma \subseteq \Psi \subseteq \Lambda $
.
$\Gamma \subseteq \Psi \subseteq \Lambda $
.
Corollary 4.8. The coefficients
![]() $ \mathfrak {b}^{\Lambda }_{\Psi ,(n)}$
are nonnegative integers with these properties:
$ \mathfrak {b}^{\Lambda }_{\Psi ,(n)}$
are nonnegative integers with these properties:
-
(a) If
 $ 0=n< |\Lambda |-|\Psi |$
or
$ 0=n< |\Lambda |-|\Psi |$
or
 $n>|\Lambda |-|\Psi |$
, then
$n>|\Lambda |-|\Psi |$
, then
 $ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} = 0$
.
$ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} = 0$
. -
(b) If
 $0 < n = |\Lambda | - |\Psi |$
, then
$0 < n = |\Lambda | - |\Psi |$
, then
 $ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} = 2^{ \mathsf {sc}+\mathsf {mc}-1}$
.
$ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} = 2^{ \mathsf {sc}+\mathsf {mc}-1}$
. -
(c) If
 $0<n = |\Lambda | - |\Psi | - 1$
, then
$0<n = |\Lambda | - |\Psi | - 1$
, then
 $ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} = 2^{\mathsf {sc}+\mathsf {mc}-2}(2\mathsf {sc}+3\mathsf {mc}+2\mathsf {fb}-3)$
.
$ \mathfrak {b}^{\Lambda }_{\Psi ,(n)} = 2^{\mathsf {sc}+\mathsf {mc}-2}(2\mathsf {sc}+3\mathsf {mc}+2\mathsf {fb}-3)$
.
Proof. If
![]() $\mathsf {mc}=0$
, then
$\mathsf {mc}=0$
, then
![]() $\mathsf {fb}=0$
,
$\mathsf {fb}=0$
,
![]() $\mathsf {sc} = |\Lambda |-|\Psi |$
,
$\mathsf {sc} = |\Lambda |-|\Psi |$
,
![]() $\mathsf {res} = 2$
and
$\mathsf {res} = 2$
and
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t) = (2t)^{\mathsf {sc}}$
. In this case, the desired properties are easy to deduce using Proposition 4.6.
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t) = (2t)^{\mathsf {sc}}$
. In this case, the desired properties are easy to deduce using Proposition 4.6.
Assume
![]() $\mathsf {mc}\geq 1$
, and let
$\mathsf {mc}\geq 1$
, and let
![]() $u=t-\beta $
. By Proposition 4.6 and Lemma 4.7,
$u=t-\beta $
. By Proposition 4.6 and Lemma 4.7,
![]() $ \mathfrak {b}^{\Lambda }_{\Psi ,(n)}$
is the coefficient of
$ \mathfrak {b}^{\Lambda }_{\Psi ,(n)}$
is the coefficient of
![]() $\beta ^{|\Lambda |-|\Psi | -n} u^{n-\mathsf {res}}$
in
$\beta ^{|\Lambda |-|\Psi | -n} u^{n-\mathsf {res}}$
in
Equivalently, this is the coefficient of
![]() $u^n$
in
$u^n$
in
![]() $2^{\mathsf {sc}} (u+1)^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2u +1)^{\mathsf {mc}-1}u^{\mathsf {res}}$
, which is clearly a nonnegative integer that is zero if
$2^{\mathsf {sc}} (u+1)^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2u +1)^{\mathsf {mc}-1}u^{\mathsf {res}}$
, which is clearly a nonnegative integer that is zero if
![]() $n<2 \leq \mathsf {res}$
or
$n<2 \leq \mathsf {res}$
or
![]() $n> \mathsf {sc}+2\mathsf {mc}+\mathsf {fb}-2 + \mathsf {res} = |\Lambda |-|\Psi |$
. It is also straightforward to extract the coefficients in parts (b) and (c) in this case.
$n> \mathsf {sc}+2\mathsf {mc}+\mathsf {fb}-2 + \mathsf {res} = |\Lambda |-|\Psi |$
. It is also straightforward to extract the coefficients in parts (b) and (c) in this case.
Recall that
![]() $\Gamma := (\Lambda _2,\Lambda _3,\Lambda _4,\dots )$
.
$\Gamma := (\Lambda _2,\Lambda _3,\Lambda _4,\dots )$
.
Lemma 4.9. If
![]() $0 \leq n \leq \Lambda _1$
is an integer, then
$0 \leq n \leq \Lambda _1$
is an integer, then
 $\displaystyle j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /(n)} = \sum _{\substack {\mu \text { strict} \\ \Gamma \subseteq \mu \subseteq \Lambda }} \mathfrak {b}^{\Lambda }_{\mu ,(n)} \cdot \beta ^{|\Lambda |-|\mu |-n}\cdot j\hspace {-0.1mm}q^{\mathrm {comb}}_\mu. $
$\displaystyle j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /(n)} = \sum _{\substack {\mu \text { strict} \\ \Gamma \subseteq \mu \subseteq \Lambda }} \mathfrak {b}^{\Lambda }_{\mu ,(n)} \cdot \beta ^{|\Lambda |-|\mu |-n}\cdot j\hspace {-0.1mm}q^{\mathrm {comb}}_\mu. $
Proof. Since we know from Theorem 4.2 that the generating function
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda }$
is symmetric, we can express
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda }$
is symmetric, we can express
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda }(t,x_1,x_2,\dots ,x_m) =j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda }(x_1,x_2,\dots ,x_m,t)$
as an element of
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda }(t,x_1,x_2,\dots ,x_m) =j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda }(x_1,x_2,\dots ,x_m,t)$
as an element of
![]() $\mathbb {Z}[t][x_1,x_2,\dots ,x_m]$
in two different ways, by letting t either record the weight contribution of the bars of
$\mathbb {Z}[t][x_1,x_2,\dots ,x_m]$
in two different ways, by letting t either record the weight contribution of the bars of
![]() $T \in \mathsf {ShBT}_Q(\Lambda )$
containing
$T \in \mathsf {ShBT}_Q(\Lambda )$
containing
![]() $1'$
or
$1'$
or
![]() $1$
, or the weight contribution of the bars containing
$1$
, or the weight contribution of the bars containing
![]() $(m+1)'$
or
$(m+1)'$
or
![]() $m+1$
. We use this ability in the following argument.
$m+1$
. We use this ability in the following argument.
Because
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\mu }(t)$
is nonzero if and only if
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\mu }(t)$
is nonzero if and only if
![]() $\ell (\mu )\leq 1$
, we have
$\ell (\mu )\leq 1$
, we have
 $$ \begin{align} \begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(t,x_1,x_2,\dots) &= \sum_{\mu\subseteq \Lambda} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu}(t)j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/\mu}(x_1,x_2,\dots) = \sum_{n=0}^{\Lambda_1} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/(n)} j\hspace{-0.1mm}q^{\mathrm{comb}}_{n}(t). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(t,x_1,x_2,\dots) &= \sum_{\mu\subseteq \Lambda} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu}(t)j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/\mu}(x_1,x_2,\dots) = \sum_{n=0}^{\Lambda_1} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/(n)} j\hspace{-0.1mm}q^{\mathrm{comb}}_{n}(t). \end{aligned} \end{align} $$
However, for any fixed
![]() $m>0$
, we have
$m>0$
, we have
 $$ \begin{align*} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(t,x_1,x_2,\dots,x_m) & = j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(x_1,x_2,\dots,x_m,t ) \\ & = \sum_{\mu \subseteq \Lambda} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu}(x_1,x_2,\dots,x_m) j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/\mu}(t). \end{align*} $$
$$ \begin{align*} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(t,x_1,x_2,\dots,x_m) & = j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(x_1,x_2,\dots,x_m,t ) \\ & = \sum_{\mu \subseteq \Lambda} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu}(x_1,x_2,\dots,x_m) j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/\mu}(t). \end{align*} $$
As the last sum is finite and since
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\mu }(t)$
is nonzero if and only if
$j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\mu }(t)$
is nonzero if and only if
![]() $\Gamma \subseteq \mu \subseteq \Lambda $
, we can take the limit as
$\Gamma \subseteq \mu \subseteq \Lambda $
, we can take the limit as
![]() $m\to \infty $
in the sense of formal power series and apply (4.1) to obtain
$m\to \infty $
in the sense of formal power series and apply (4.1) to obtain
 $$\begin{align*}\begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(t, x_1,x_2,\dots) & = \sum_{\Gamma \subseteq \mu \subseteq \Lambda} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/\mu}(t) \\ & = \sum_{n\geq 0} \sum_{\Gamma \subseteq \mu \subseteq \Lambda} \mathfrak{b}^{\Lambda}_{\mu,(n)} \beta^{|\Lambda|-|\mu| -n} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu} j\hspace{-0.1mm}q^{\mathrm{comb}}_{n}(t). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda}(t, x_1,x_2,\dots) & = \sum_{\Gamma \subseteq \mu \subseteq \Lambda} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\Lambda/\mu}(t) \\ & = \sum_{n\geq 0} \sum_{\Gamma \subseteq \mu \subseteq \Lambda} \mathfrak{b}^{\Lambda}_{\mu,(n)} \beta^{|\Lambda|-|\mu| -n} j\hspace{-0.1mm}q^{\mathrm{comb}}_{\mu} j\hspace{-0.1mm}q^{\mathrm{comb}}_{n}(t). \end{aligned} \end{align*}$$
The lemma follows by equating coefficients of
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_n(t)$
in this equation and (4.2).
$j\hspace {-0.1mm}q^{\mathrm {comb}}_n(t)$
in this equation and (4.2).
Since
![]() $\Lambda \supseteq \Psi \supseteq \Gamma = (\Lambda _2,\Lambda _3,\dots )$
, the skew shape
$\Lambda \supseteq \Psi \supseteq \Gamma = (\Lambda _2,\Lambda _3,\dots )$
, the skew shape
![]() $\textsf {SD}_{\Psi /\Gamma }$
is also a shifted ribbon. A removable corner box
$\textsf {SD}_{\Psi /\Gamma }$
is also a shifted ribbon. A removable corner box
![]() $(i,j) \in \textsf {SD}_\Gamma $
can be added to
$(i,j) \in \textsf {SD}_\Gamma $
can be added to
![]() $\textsf {SD}_{\Psi /\Gamma }$
to form a shifted ribbon if and only if
$\textsf {SD}_{\Psi /\Gamma }$
to form a shifted ribbon if and only if
![]() $(i+1,j+1) \notin \textsf {SD}_{\Psi /\Gamma }$
. Let
$(i+1,j+1) \notin \textsf {SD}_{\Psi /\Gamma }$
. Let
![]() $\mathcal {R}$
be the set of such boxes
$\mathcal {R}$
be the set of such boxes
![]() $(i,j) \in \textsf {SD}_\Gamma $
. If
$(i,j) \in \textsf {SD}_\Gamma $
. If
![]() $\Lambda = (15,12,9,6,3,1)$
and
$\Lambda = (15,12,9,6,3,1)$
and
![]() $\Psi = (13,9,7,6,2)$
, then the boxes
$\Psi = (13,9,7,6,2)$
, then the boxes
![]() $(i,j) \in \mathcal {R}$
are the ones marked as
$(i,j) \in \mathcal {R}$
are the ones marked as
![]() $\mathcal {U}$
,
$\mathcal {U}$
,
![]() ${\mathcal {V}}$
or
${\mathcal {V}}$
or
![]() ${\mathcal {W}}$
below, with
${\mathcal {W}}$
below, with
![]() $\textsf {SD}_{\Psi /\Gamma }$
shown in gray:
$\textsf {SD}_{\Psi /\Gamma }$
shown in gray:

We divide
![]() $\mathcal {R}$
into three disjoint subsets. Let
$\mathcal {R}$
into three disjoint subsets. Let
![]() $\mathcal {U}$
be the set of boxes
$\mathcal {U}$
be the set of boxes
![]() $(i,j)\in \mathcal {R}$
with
$(i,j)\in \mathcal {R}$
with
![]() $i=j$
and
$i=j$
and
![]() $(i,j+1) \in \textsf {SD}_{\Psi /\Gamma }$
or with
$(i,j+1) \in \textsf {SD}_{\Psi /\Gamma }$
or with
![]() $i\neq j$
and
$i\neq j$
and
![]() $(i,j+1),(i+1,j) \in \textsf {SD}_{\Psi /\Gamma }$
. Let
$(i,j+1),(i+1,j) \in \textsf {SD}_{\Psi /\Gamma }$
. Let
![]() ${\mathcal {V}}$
be the set of boxes
${\mathcal {V}}$
be the set of boxes
![]() $(i,j) \in \mathcal {R}$
either with
$(i,j) \in \mathcal {R}$
either with
![]() $i=j$
and
$i=j$
and
![]() $(i,j+1) \notin \textsf {SD}_{\Psi /\Gamma }$
or such that
$(i,j+1) \notin \textsf {SD}_{\Psi /\Gamma }$
or such that
![]() $i\neq j$
and exactly one of
$i\neq j$
and exactly one of
![]() $(i,j+1)$
or
$(i,j+1)$
or
![]() $(i+1,j)$
belongs to
$(i+1,j)$
belongs to
![]() $\textsf {SD}_{\Psi /\Gamma }$
. Let
$\textsf {SD}_{\Psi /\Gamma }$
. Let
![]() ${\mathcal {W}}$
be the set of all other boxes
${\mathcal {W}}$
be the set of all other boxes
![]() $(i,j) \in \mathcal {R}$
. In our example above, the cells of
$(i,j) \in \mathcal {R}$
. In our example above, the cells of
![]() $\mathcal {R}$
are labeled according to the decomposition
$\mathcal {R}$
are labeled according to the decomposition
![]() $\mathcal {R} =\mathcal {U}\sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
.
$\mathcal {R} =\mathcal {U}\sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
.
Lemma 4.10. Suppose
![]() $\Lambda _1 - \Psi _1 \geq 2$
. Then
$\Lambda _1 - \Psi _1 \geq 2$
. Then
![]() $ |\mathcal {U}| = \mathsf {sc} $
and
$ |\mathcal {U}| = \mathsf {sc} $
and
![]() $ |{\mathcal {V}}| + 2|{\mathcal {W}}| = \mathsf {mc} + \mathsf {fb} -1$
.
$ |{\mathcal {V}}| + 2|{\mathcal {W}}| = \mathsf {mc} + \mathsf {fb} -1$
.
Proof. Since
![]() $\Lambda _1 \geq \Psi _1 +2$
, it is clear that
$\Lambda _1 \geq \Psi _1 +2$
, it is clear that
![]() $ |\mathcal {U}| = \mathsf {sc}$
and
$ |\mathcal {U}| = \mathsf {sc}$
and
![]() $\mathsf {mc}\geq 1$
. Observe that a position
$\mathsf {mc}\geq 1$
. Observe that a position
![]() $(i,j)$
belongs to
$(i,j)$
belongs to
![]() ${\mathcal {V}}$
if and only if either
${\mathcal {V}}$
if and only if either
![]() $(i+1,j+1)$
and
$(i+1,j+1)$
and
![]() $(i,j+1)$
are the first two boxes of a connected component of
$(i,j+1)$
are the first two boxes of a connected component of
![]() $\textsf {SD}_{\Lambda /\Psi }$
in the usual row reading order, or
$\textsf {SD}_{\Lambda /\Psi }$
in the usual row reading order, or
![]() $(i+1,j)$
and
$(i+1,j)$
and
![]() $(i+1,j+1)$
are the last two boxes of a connected component of
$(i+1,j+1)$
are the last two boxes of a connected component of
![]() $\textsf {SD}_{\Lambda /\Psi }$
that does not end in the first row. However, a position
$\textsf {SD}_{\Lambda /\Psi }$
that does not end in the first row. However, a position
![]() $(i,j)$
belongs to
$(i,j)$
belongs to
![]() ${\mathcal {W}}$
if and only if all three of the boxes
${\mathcal {W}}$
if and only if all three of the boxes
![]() $(i+1,j)$
,
$(i+1,j)$
,
![]() $(i+1,j+1)$
,
$(i+1,j+1)$
,
![]() $(i,j+1)$
belong to a connected component of
$(i,j+1)$
belong to a connected component of
![]() $\textsf {SD}_{\Lambda /\Psi }$
, in which case
$\textsf {SD}_{\Lambda /\Psi }$
, in which case
![]() $(i,j+1)$
is a forced box.
$(i,j+1)$
is a forced box.
Now choose a connected component
![]() $\mathcal {C}\subseteq \textsf {SD}_{\Lambda /\Psi }$
with multiple boxes. In this component, compare the number
$\mathcal {C}\subseteq \textsf {SD}_{\Lambda /\Psi }$
with multiple boxes. In this component, compare the number
![]() $p $
of boxes
$p $
of boxes
![]() $(i,j)$
with
$(i,j)$
with
![]() $(i-1,j-1) \in {\mathcal {V}}\sqcup {\mathcal {W}} $
with the number q of forced boxes
$(i-1,j-1) \in {\mathcal {V}}\sqcup {\mathcal {W}} $
with the number q of forced boxes
![]() $(i,j)$
that have
$(i,j)$
that have
![]() $(i,j-1) \notin {\mathcal {W}}$
– that is, appearing as
$(i,j-1) \notin {\mathcal {W}}$
– that is, appearing as
![]() $\bullet $
in a configuration like
$\bullet $
in a configuration like ![]() but not
but not ![]() . If
. If
![]() $\mathcal {F}$
is the set of forced boxes and we set
$\mathcal {F}$
is the set of forced boxes and we set
![]() $\hat {\mathcal {V}} := \{(i+1,j+1) : (i,j) \in {\mathcal {V}}\}$
and
$\hat {\mathcal {V}} := \{(i+1,j+1) : (i,j) \in {\mathcal {V}}\}$
and
![]() $\hat {\mathcal {W}} := \{(i+1,j+1):(i,j) \in {\mathcal {W}}\}$
, then
$\hat {\mathcal {W}} := \{(i+1,j+1):(i,j) \in {\mathcal {W}}\}$
, then
![]() $p = |\hat {\mathcal {V}} \cap \mathcal {C}| + |\hat {\mathcal {W}} \cap \mathcal {C}|$
and
$p = |\hat {\mathcal {V}} \cap \mathcal {C}| + |\hat {\mathcal {W}} \cap \mathcal {C}|$
and
![]() $q= |\mathcal {F}\cap \mathcal {C}| - |\hat {\mathcal {W}} \cap \mathcal {C}| $
.
$q= |\mathcal {F}\cap \mathcal {C}| - |\hat {\mathcal {W}} \cap \mathcal {C}| $
.
We can reinterpret p and q in terms of the shape of a modified version of
![]() $\mathcal {C}$
. If
$\mathcal {C}$
. If
![]() $\mathcal {C}$
starts with two boxes
$\mathcal {C}$
starts with two boxes
![]() $(i,j),(i-1,j)$
in the same column (so that
$(i,j),(i-1,j)$
in the same column (so that
![]() $(i,j) \in \hat {\mathcal {V}}$
and
$(i,j) \in \hat {\mathcal {V}}$
and
![]() $(i-1,j-1) \in {\mathcal {V}}$
), then add
$(i-1,j-1) \in {\mathcal {V}}$
), then add
![]() $(i,j-1)$
to the component. Likewise, if
$(i,j-1)$
to the component. Likewise, if
![]() $\mathcal {C}$
ends with two boxes
$\mathcal {C}$
ends with two boxes
![]() $(i,j-1),(i,j)$
in the same row (so that if
$(i,j-1),(i,j)$
in the same row (so that if
![]() $i>1$
, then
$i>1$
, then
![]() $(i,j) \in \hat {\mathcal {V}}$
and
$(i,j) \in \hat {\mathcal {V}}$
and
![]() $(i-1,j-1) \in {\mathcal {V}}$
), then add
$(i-1,j-1) \in {\mathcal {V}}$
), then add
![]() $(i-1,j)$
to the component. Then in our modified component, the configurations of the form
$(i-1,j)$
to the component. Then in our modified component, the configurations of the form ![]() and
and ![]() interleave, with one more
interleave, with one more ![]() configuration than
configuration than ![]() configuration. Moreover, by construction, the number of
configuration. Moreover, by construction, the number of ![]() configurations is q and the number of
configurations is q and the number of ![]() configurations is p, except when
configurations is p, except when
![]() $\mathcal {C}$
ends with two boxes in the first row, in which case the number of configurations of the latter form is
$\mathcal {C}$
ends with two boxes in the first row, in which case the number of configurations of the latter form is
![]() $p-1$
. Thus, if
$p-1$
. Thus, if
![]() $\mathcal {C}$
ends with two boxes in the first row, then
$\mathcal {C}$
ends with two boxes in the first row, then
![]() $p-q=0$
and otherwise we have
$p-q=0$
and otherwise we have
![]() $p-q=1$
.
$p-q=1$
.
Since
![]() $\Lambda _1 \geq \Psi _1 +2$
, the last connected component of
$\Lambda _1 \geq \Psi _1 +2$
, the last connected component of
![]() $\textsf {SD}_{\Lambda /\Psi }$
ends with two boxes in the first row, and no other connected component of
$\textsf {SD}_{\Lambda /\Psi }$
ends with two boxes in the first row, and no other connected component of
![]() $\textsf {SD}_{\Lambda /\Psi }$
has this property. By summing
$\textsf {SD}_{\Lambda /\Psi }$
has this property. By summing
![]() $p-q$
over all connected components
$p-q$
over all connected components
![]() $\mathcal {C}$
with multiple boxes, we obtain
$\mathcal {C}$
with multiple boxes, we obtain
![]() $(|\hat {\mathcal {V}}| + |\hat {\mathcal {W}}|) - (|\mathcal {F}| - |\hat {\mathcal {W}}|) = \mathsf {mc} -1$
. As
$(|\hat {\mathcal {V}}| + |\hat {\mathcal {W}}|) - (|\mathcal {F}| - |\hat {\mathcal {W}}|) = \mathsf {mc} -1$
. As
![]() $|\mathcal {F}| = \mathsf {fb}$
,
$|\mathcal {F}| = \mathsf {fb}$
,
![]() $|\hat {\mathcal {V}}| = |{\mathcal {V}}|$
, and
$|\hat {\mathcal {V}}| = |{\mathcal {V}}|$
, and
![]() $|\hat {\mathcal {W}}| =|{\mathcal {W}}|$
, we can rewrite this identity as
$|\hat {\mathcal {W}}| =|{\mathcal {W}}|$
, we can rewrite this identity as
![]() $|{\mathcal {V}}| + 2|{\mathcal {W}}| - \mathsf {fb} = \mathsf {mc}-1$
.
$|{\mathcal {V}}| + 2|{\mathcal {W}}| - \mathsf {fb} = \mathsf {mc}-1$
.
Lemma 4.11. Let u be an indeterminate and suppose
![]() $\Lambda _1 - \Psi _1 \geq 2$
. Then
$\Lambda _1 - \Psi _1 \geq 2$
. Then
Proof. Call a position in a shifted ribbon free if it is not on the diagonal but is the first box in its connected component in row reading order. By Proposition 2.7, the number
![]() $ \widehat b^\Psi _{\Gamma ,(n)}$
counts the ways that we can add a subset of removable corner boxes of
$ \widehat b^\Psi _{\Gamma ,(n)}$
counts the ways that we can add a subset of removable corner boxes of
![]() $\textsf {SD}_\Gamma $
to
$\textsf {SD}_\Gamma $
to
![]() $\textsf {SD}_{\Psi /\Gamma }$
to form a shifted ribbon, and then assign either
$\textsf {SD}_{\Psi /\Gamma }$
to form a shifted ribbon, and then assign either
![]() $1$
or
$1$
or
![]() $1'$
or
$1'$
or
![]() $1'1$
to each free box in this ribbon, such that the number of boxes plus the number of entries equal to
$1'1$
to each free box in this ribbon, such that the number of boxes plus the number of entries equal to
![]() $1'1$
is n.
$1'1$
is n.
The shifted ribbons that can be formed by adding corner boxes of
![]() $\textsf {SD}_\Gamma $
to
$\textsf {SD}_\Gamma $
to
![]() $\textsf {SD}_{\Psi /\Gamma }$
are the unions of
$\textsf {SD}_{\Psi /\Gamma }$
are the unions of
![]() $\textsf {SD}_{\Psi /\Gamma }$
with arbitrary subsets of
$\textsf {SD}_{\Psi /\Gamma }$
with arbitrary subsets of
![]() $\mathcal {U}\sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
. Consider the number of free boxes in a ribbon formed by successively adding positions from
$\mathcal {U}\sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
. Consider the number of free boxes in a ribbon formed by successively adding positions from
![]() $\mathcal {U}\sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
to
$\mathcal {U}\sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
to
![]() $\textsf {SD}_{\Psi /\Gamma }$
. Each time we add a box from
$\textsf {SD}_{\Psi /\Gamma }$
. Each time we add a box from
![]() $\mathcal {U}$
, this number is reduced by one, since the added box either merges two connected components or changes the first box in a connected component from an off-diagonal position
$\mathcal {U}$
, this number is reduced by one, since the added box either merges two connected components or changes the first box in a connected component from an off-diagonal position
![]() $(i,i+1)$
to a diagonal position
$(i,i+1)$
to a diagonal position
![]() $(i,i)$
. The number of free boxes is unchanged when we add a box from
$(i,i)$
. The number of free boxes is unchanged when we add a box from
![]() ${\mathcal {V}}$
, since the added box will either be an isolated position on the diagonal or adjacent to exactly one connected component. Finally, the number of free boxes increases by one each time we add a box from
${\mathcal {V}}$
, since the added box will either be an isolated position on the diagonal or adjacent to exactly one connected component. Finally, the number of free boxes increases by one each time we add a box from
![]() ${\mathcal {W}}$
to
${\mathcal {W}}$
to
![]() $\textsf {SD}_{\Psi /\Gamma }$
, since the added box will always be an isolated position not on the diagonal.
$\textsf {SD}_{\Psi /\Gamma }$
, since the added box will always be an isolated position not on the diagonal.
If
![]() $\textsf {SD}_{\Psi /\Gamma }$
intersects the diagonal, then it has the same number
$\textsf {SD}_{\Psi /\Gamma }$
intersects the diagonal, then it has the same number
![]() $\mathsf {sc}+\mathsf {mc}$
of connected components as
$\mathsf {sc}+\mathsf {mc}$
of connected components as
![]() $\textsf {SD}_{\Lambda /\Psi }$
; otherwise, its number of connected components is
$\textsf {SD}_{\Lambda /\Psi }$
; otherwise, its number of connected components is
![]() $\mathsf {sc}+\mathsf {mc}-1$
. Either way, the number of free boxes in
$\mathsf {sc}+\mathsf {mc}-1$
. Either way, the number of free boxes in
![]() $\textsf {SD}_{\Psi /\Gamma }$
is
$\textsf {SD}_{\Psi /\Gamma }$
is
![]() $\mathsf {sc}+\mathsf {mc}-1$
. Given these observations and Lemma 4.10, we deduce that
$\mathsf {sc}+\mathsf {mc}-1$
. Given these observations and Lemma 4.10, we deduce that
 $$\begin{align*}\begin{aligned} \sum_{n \geq 0} \widehat b^\Psi_{\Gamma,(n)} u^{n } &= u ^{|\Psi|-|\Gamma|}(2 + u)^{\mathsf{sc}+\mathsf{mc}-1}(1 + \tfrac{u}{2+u})^{|\mathcal{U}|}(1+u)^{|{\mathcal{V}}|} (1 + u(2+u))^{|{\mathcal{W}}|} \\& = 2^{\mathsf{sc}} u ^{|\Psi|-|\Gamma|} (2+u)^{\mathsf{mc}-1} (1+u)^{\mathsf{sc}+\mathsf{mc}+\mathsf{fb}-1}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \sum_{n \geq 0} \widehat b^\Psi_{\Gamma,(n)} u^{n } &= u ^{|\Psi|-|\Gamma|}(2 + u)^{\mathsf{sc}+\mathsf{mc}-1}(1 + \tfrac{u}{2+u})^{|\mathcal{U}|}(1+u)^{|{\mathcal{V}}|} (1 + u(2+u))^{|{\mathcal{W}}|} \\& = 2^{\mathsf{sc}} u ^{|\Psi|-|\Gamma|} (2+u)^{\mathsf{mc}-1} (1+u)^{\mathsf{sc}+\mathsf{mc}+\mathsf{fb}-1}. \end{aligned}\end{align*}$$
This becomes the desired identity after dividing both sides by
![]() $u ^{|\Psi |-|\Gamma |}$
, replacing u by
$u ^{|\Psi |-|\Gamma |}$
, replacing u by
![]() $\beta u^{-1}$
, and then multiplying both sides by
$\beta u^{-1}$
, and then multiplying both sides by
![]() $u^{\mathsf {sc}+2\mathsf {mc}+\mathsf {fb}-2} = u^{|\Lambda |-|\Psi |-\mathsf {res}} =u^{\Lambda _1-\mathsf {res}+ |\Gamma |-|\Psi | }$
.
$u^{\mathsf {sc}+2\mathsf {mc}+\mathsf {fb}-2} = u^{|\Lambda |-|\Psi |-\mathsf {res}} =u^{\Lambda _1-\mathsf {res}+ |\Gamma |-|\Psi | }$
.
The following lemma is the most technical part of our argument.
Lemma 4.12. If
![]() $n = \Lambda _1 - \Lambda _2$
and
$n = \Lambda _1 - \Lambda _2$
and
![]() $m=\Lambda _2>0$
, then
$m=\Lambda _2>0$
, then
 $$\begin{align*}\widehat b^\Psi_{\Gamma,(n)} - \mathfrak{b}^{\Lambda}_{\Psi,(m)} = \begin{cases} 1 &\text{if}\ \Psi = (\Lambda_1,\Lambda_3,\Lambda_4,\dots)\\ 1 &\text{if}\ \Psi = (\Lambda_1-1,\Lambda_3,\Lambda_4,\dots) \\ 0&\text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\widehat b^\Psi_{\Gamma,(n)} - \mathfrak{b}^{\Lambda}_{\Psi,(m)} = \begin{cases} 1 &\text{if}\ \Psi = (\Lambda_1,\Lambda_3,\Lambda_4,\dots)\\ 1 &\text{if}\ \Psi = (\Lambda_1-1,\Lambda_3,\Lambda_4,\dots) \\ 0&\text{otherwise}. \end{cases}\end{align*}$$
Proof. If
![]() $\Lambda _1 - \Psi _1 \geq 2$
, then
$\Lambda _1 - \Psi _1 \geq 2$
, then
![]() $\widehat b^\Psi _{\Gamma ,(n)} = \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
for any integers n and m with
$\widehat b^\Psi _{\Gamma ,(n)} = \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
for any integers n and m with
![]() $n+m = \Lambda _1$
. For
$n+m = \Lambda _1$
. For
![]() $m \geq 2$
, this is because if we set
$m \geq 2$
, this is because if we set
![]() $u=t-\beta $
, then comparing Proposition 4.6 and Lemma 4.7 shows that
$u=t-\beta $
, then comparing Proposition 4.6 and Lemma 4.7 shows that
![]() $ \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
is the coefficient of
$ \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
is the coefficient of
![]() $\beta ^{|\Lambda |-|\Psi | -m} u^{m-\mathsf {res}}$
in
$\beta ^{|\Lambda |-|\Psi | -m} u^{m-\mathsf {res}}$
in
![]() $2^{\mathsf {sc}} (u+\beta )^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2u +\beta )^{\mathsf {mc}-1} $
, and by Lemma 4.11, this is also equal to
$2^{\mathsf {sc}} (u+\beta )^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2u +\beta )^{\mathsf {mc}-1} $
, and by Lemma 4.11, this is also equal to
![]() $\widehat b^\Psi _{\Gamma ,(n)}$
when
$\widehat b^\Psi _{\Gamma ,(n)}$
when
![]() $m= \Lambda _1-n$
. For
$m= \Lambda _1-n$
. For
![]() $m\leq 1$
, we have that
$m\leq 1$
, we have that
![]() $\widehat b^\Psi _{\Gamma ,(n)}$
,
$\widehat b^\Psi _{\Gamma ,(n)}$
,
![]() $ \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
, and the relevant coefficients in
$ \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
, and the relevant coefficients in
![]() $2^{\mathsf {sc}} (u+\beta )^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2u +\beta )^{\mathsf {mc}-1} $
are all zero.
$2^{\mathsf {sc}} (u+\beta )^{\mathsf {sc}+\mathsf {mc}+\mathsf {fb}-1} (2u +\beta )^{\mathsf {mc}-1} $
are all zero.
It remains to check the desired identity when
![]() $\Lambda _1 -\Psi _1 \in \{0,1\}$
. From this point on, we fix
$\Lambda _1 -\Psi _1 \in \{0,1\}$
. From this point on, we fix
![]() $n=\Lambda _1-\Lambda _2$
and
$n=\Lambda _1-\Lambda _2$
and
![]() $m=\Lambda _2>0$
; in particular, in these cases,
$m=\Lambda _2>0$
; in particular, in these cases,
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Gamma $
are both nonempty. If
$\Gamma $
are both nonempty. If
![]() $|\Psi | - |\Gamma |>n$
, then
$|\Psi | - |\Gamma |>n$
, then
![]() $|\Lambda | - |\Psi | = \Lambda _1 - (|\Psi | - |\Gamma | )<\Lambda _1 - n= m$
and it follows from Proposition 2.7 and Corollary 4.8 that
$|\Lambda | - |\Psi | = \Lambda _1 - (|\Psi | - |\Gamma | )<\Lambda _1 - n= m$
and it follows from Proposition 2.7 and Corollary 4.8 that
![]() $\widehat b^\Psi _{\Gamma ,(n)} = \mathfrak {b}^{\Lambda }_{\Psi ,(m)}= 0$
as desired. We may therefore assume
$\widehat b^\Psi _{\Gamma ,(n)} = \mathfrak {b}^{\Lambda }_{\Psi ,(m)}= 0$
as desired. We may therefore assume
![]() $|\Psi | - |\Gamma | \leq n$
. There are three cases:
$|\Psi | - |\Gamma | \leq n$
. There are three cases:
-
(1) Suppose
 $\Lambda _1 = \Psi _1$
. Then
$\Lambda _1 = \Psi _1$
. Then
 $|\Psi | - |\Gamma | \geq \Psi _1 - \Gamma _1 = n$
also holds, so
$|\Psi | - |\Gamma | \geq \Psi _1 - \Gamma _1 = n$
also holds, so
 $|\Psi | - |\Gamma | = n$
and
$|\Psi | - |\Gamma | = n$
and
 $|\Lambda | - |\Psi | = m$
. Since
$|\Lambda | - |\Psi | = m$
. Since
 $\Psi _1-\Gamma _1 = \Lambda _1-\Lambda _2 = n$
, it follows that
$\Psi _1-\Gamma _1 = \Lambda _1-\Lambda _2 = n$
, it follows that  $$\begin{align*}\Psi = (\Lambda_1,\Lambda_3,\Lambda_4,\dots) = \Gamma + (n,0,0,\dots),\end{align*}$$
$$\begin{align*}\Psi = (\Lambda_1,\Lambda_3,\Lambda_4,\dots) = \Gamma + (n,0,0,\dots),\end{align*}$$
and we wish to show that
 $ \widehat b^\Psi _{\Gamma ,(n)} =1 + \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
. This holds as
$ \widehat b^\Psi _{\Gamma ,(n)} =1 + \mathfrak {b}^{\Lambda }_{\Psi ,(m)}$
. This holds as
 $\mathsf {sc}+\mathsf {mc}=1$
so
$\mathsf {sc}+\mathsf {mc}=1$
so
 $ \mathfrak {b}^{\Lambda }_{\Psi ,(m)} = 2^{\mathsf {sc}+\mathsf {mc}-1} = 1$
while
$ \mathfrak {b}^{\Lambda }_{\Psi ,(m)} = 2^{\mathsf {sc}+\mathsf {mc}-1} = 1$
while
 $ \widehat b^\Psi _{\Gamma ,(n)} = |\mathsf {ShRibbons}_P(\Psi /\hspace {-1mm}/\Gamma ;n)| =2$
by Corollary 4.8 and Proposition 2.7.
$ \widehat b^\Psi _{\Gamma ,(n)} = |\mathsf {ShRibbons}_P(\Psi /\hspace {-1mm}/\Gamma ;n)| =2$
by Corollary 4.8 and Proposition 2.7. -
(2) Suppose
 $\Lambda _1 - \Psi _1 = 1$
. Then
$\Lambda _1 - \Psi _1 = 1$
. Then
 $ |\Psi | - |\Gamma | \geq \Psi _1 - \Gamma _1 = n-1$
so we have
$ |\Psi | - |\Gamma | \geq \Psi _1 - \Gamma _1 = n-1$
so we have
 $ |\Psi | - |\Gamma | \in \{n-1,n\}$
. If
$ |\Psi | - |\Gamma | \in \{n-1,n\}$
. If
 $|\Psi | - |\Gamma | =n$
, then
$|\Psi | - |\Gamma | =n$
, then
 $|\Lambda | - |\Psi | = m$
and
$|\Lambda | - |\Psi | = m$
and
 $\textsf {SD}_{\Psi /\Gamma }$
consists of the
$\textsf {SD}_{\Psi /\Gamma }$
consists of the
 $n-1$
boxes
$n-1$
boxes
 $(1,j) $
with
$(1,j) $
with
 $ \Lambda _2 < j < \Lambda _1$
plus one box
$ \Lambda _2 < j < \Lambda _1$
plus one box
 $(i,j) \in \textsf {SD}_{\Lambda /\Gamma }$
with
$(i,j) \in \textsf {SD}_{\Lambda /\Gamma }$
with
 $i>1$
. In this event, Corollary 4.8 tells us that
$i>1$
. In this event, Corollary 4.8 tells us that
 $ \mathfrak {b}^{\Lambda }_{\Psi ,(m)} = 2^{\mathsf {sc}+\mathsf {mc}-1}$
, while Proposition 2.7 tells us that
$ \mathfrak {b}^{\Lambda }_{\Psi ,(m)} = 2^{\mathsf {sc}+\mathsf {mc}-1}$
, while Proposition 2.7 tells us that
 $\widehat b^\Psi _{\Gamma ,(n)}=2^e$
, where
$\widehat b^\Psi _{\Gamma ,(n)}=2^e$
, where
 $e \in \{0,1,2\} $
is the number of connected components in
$e \in \{0,1,2\} $
is the number of connected components in
 $\textsf {SD}_{\Psi /\Gamma }$
not intersecting the diagonal. As
$\textsf {SD}_{\Psi /\Gamma }$
not intersecting the diagonal. As
 $\mathsf {sc}+\mathsf {mc}$
is the number of connected components in
$\mathsf {sc}+\mathsf {mc}$
is the number of connected components in
 $\textsf {SD}_{\Lambda /\Psi }$
, it follows that
$\textsf {SD}_{\Lambda /\Psi }$
, it follows that
 $e=\mathsf {sc}+\mathsf {mc}-1$
, so
$e=\mathsf {sc}+\mathsf {mc}-1$
, so
 $\widehat b^\Psi _{\Gamma ,(n)} = \mathfrak {b}^{\Lambda }_{\Psi ,(m)} $
as claimed.
$\widehat b^\Psi _{\Gamma ,(n)} = \mathfrak {b}^{\Lambda }_{\Psi ,(m)} $
as claimed. -
(3) Suppose
 $\Lambda _1 - \Psi _1 = 1$
and
$\Lambda _1 - \Psi _1 = 1$
and
 $|\Psi | - |\Gamma | =n-1$
so that
$|\Psi | - |\Gamma | =n-1$
so that
 $|\Lambda | - |\Psi | = m+1$
. Since
$|\Lambda | - |\Psi | = m+1$
. Since
 $\Psi _1 - \Gamma _1=n-1$
, we can therefore write
$\Psi _1 - \Gamma _1=n-1$
, we can therefore write  $$\begin{align*}\Psi = (\Lambda_1-1,\Lambda_3,\Lambda_4,\dots) = \Gamma + (n-1,0,0,\dots),\end{align*}$$
$$\begin{align*}\Psi = (\Lambda_1-1,\Lambda_3,\Lambda_4,\dots) = \Gamma + (n-1,0,0,\dots),\end{align*}$$
so we wish to show that
 $ \widehat b^\Psi _{\Gamma ,(n)} - \mathfrak {b}^{\Lambda }_{\Psi ,(m)}=1$
. There are three subcases:
$ \widehat b^\Psi _{\Gamma ,(n)} - \mathfrak {b}^{\Lambda }_{\Psi ,(m)}=1$
. There are three subcases:-
• If
 $n=1$
, then
$n=1$
, then
 $\Psi =\Gamma $
so
$\Psi =\Gamma $
so
 $\mathsf {sc}=0$
,
$\mathsf {sc}=0$
,
 $\mathsf {mc}=1$
, and
$\mathsf {mc}=1$
, and  $$\begin{align*}\mathfrak{b}^{\Lambda}_{\Psi,(m)}=2^{\mathsf{sc}+\mathsf{mc}-2}(2\mathsf{sc}+3\mathsf{mc}+2\mathsf{fb}-3)=\mathsf{fb}\end{align*}$$
$$\begin{align*}\mathfrak{b}^{\Lambda}_{\Psi,(m)}=2^{\mathsf{sc}+\mathsf{mc}-2}(2\mathsf{sc}+3\mathsf{mc}+2\mathsf{fb}-3)=\mathsf{fb}\end{align*}$$
by Corollary 4.8. At the same time, it follows from Proposition 2.7 that
 $\widehat b^\Psi _{\Gamma ,(n)}=f+2g$
, where
$\widehat b^\Psi _{\Gamma ,(n)}=f+2g$
, where
 $f \in \{0,1\}$
and
$f \in \{0,1\}$
and
 $g\geq 0$
are the numbers of removable corner boxes of
$g\geq 0$
are the numbers of removable corner boxes of
 $\textsf {SD}_\Gamma $
on and off the diagonal. One checks that
$\textsf {SD}_\Gamma $
on and off the diagonal. One checks that
 $\mathsf {fb}+1=f+2g$
in this situation, as illustrated in Figure 4.
$\mathsf {fb}+1=f+2g$
in this situation, as illustrated in Figure 4.
Figure 4 Case (3) in the proof of Lemma 4.12: the subcase when
 $n = 1$
,
$n = 1$
,
 $\Psi = \Gamma $
. Forced boxes in
$\Psi = \Gamma $
. Forced boxes in
 $\textsf {SD}_{\Lambda / \Psi }$
are denoted by
$\textsf {SD}_{\Lambda / \Psi }$
are denoted by
 $\bullet $
, removable corners of
$\bullet $
, removable corners of
 $\textsf {SD}_{\Gamma }$
off the diagonal are denoted by
$\textsf {SD}_{\Gamma }$
off the diagonal are denoted by
 $\times $
, and removable corners on the diagonal are denoted by
$\times $
, and removable corners on the diagonal are denoted by
 $*$
.
$*$
. -
• If
 $\Gamma =(1)$
and
$\Gamma =(1)$
and
 $n>1$
, so that
$n>1$
, so that
 $\Psi =(n)$
and
$\Psi =(n)$
and
 $\Lambda = (n+1,1)$
, then
$\Lambda = (n+1,1)$
, then
 $\mathsf {sc}=2$
and
$\mathsf {sc}=2$
and
 $\mathsf {mc}=\mathsf {fb}=0$
, and one can check via Proposition 2.7 and Corollary 4.8 that
$\mathsf {mc}=\mathsf {fb}=0$
, and one can check via Proposition 2.7 and Corollary 4.8 that
 $\widehat b^\Psi _{\Gamma ,(n)} =2$
while
$\widehat b^\Psi _{\Gamma ,(n)} =2$
while
 $ \mathfrak {b}^{\Lambda }_{\Psi ,(m)}=1$
.
$ \mathfrak {b}^{\Lambda }_{\Psi ,(m)}=1$
. -
• If
 $\Gamma \neq (1)$
and
$\Gamma \neq (1)$
and
 $n>1$
, then
$n>1$
, then
 $\mathsf {sc}=\mathsf {mc}=1$
, so
$\mathsf {sc}=\mathsf {mc}=1$
, so  $$\begin{align*}\mathfrak{b}^{\Lambda}_{\Psi,(m)} =2^{\mathsf{sc}+\mathsf{mc}-2}(2\mathsf{sc}+3\mathsf{mc}+2\mathsf{fb}-3)= 2(\mathsf{fb}+1)\end{align*}$$
$$\begin{align*}\mathfrak{b}^{\Lambda}_{\Psi,(m)} =2^{\mathsf{sc}+\mathsf{mc}-2}(2\mathsf{sc}+3\mathsf{mc}+2\mathsf{fb}-3)= 2(\mathsf{fb}+1)\end{align*}$$
by Corollary 4.8, while Proposition 2.7 implies that
 $\widehat b^\Psi _{\Gamma ,(n)} = 1 + 2i + 2j +4k$
, where
$\widehat b^\Psi _{\Gamma ,(n)} = 1 + 2i + 2j +4k$
, where
 $i\in \{0,1\}$
,
$i\in \{0,1\}$
,
 $j\in \{0,1\}$
, and
$j\in \{0,1\}$
, and
 $k\geq 0$
are the numbers of removable corner boxes of
$k\geq 0$
are the numbers of removable corner boxes of
 $\textsf {SD}_\Gamma $
which are respectively in the first row, on the diagonal, or neither in the first row nor on the diagonal. One checks that
$\textsf {SD}_\Gamma $
which are respectively in the first row, on the diagonal, or neither in the first row nor on the diagonal. One checks that
 $\mathsf {fb}+1=i+j+2k$
in this situation, as illustrated in Figure 5.
$\mathsf {fb}+1=i+j+2k$
in this situation, as illustrated in Figure 5.
Figure 5 Case (3) in the proof of Lemma 4.12: the subcase when
 $n> 1$
,
$n> 1$
,
 $\Psi \neq (1)$
. Left column
$\Psi \neq (1)$
. Left column
 $i = 0$
, right column
$i = 0$
, right column
 $i = 1$
; top row
$i = 1$
; top row
 $j = 0$
, bottom row
$j = 0$
, bottom row
 $j = 1$
. The blue cells represent
$j = 1$
. The blue cells represent
 $\Psi / \Gamma $
.
$\Psi / \Gamma $
.
In each subcase, we have
 $ \widehat b^\Psi _{\Gamma ,(n)} - \mathfrak {b}^{\Lambda }_{\Psi ,(m)}=1$
, as desired.
$ \widehat b^\Psi _{\Gamma ,(n)} - \mathfrak {b}^{\Lambda }_{\Psi ,(m)}=1$
, as desired. -
This case analysis concludes the proof.
By putting everything together, we can prove our first main theorem.
Theorem 4.13. If
![]() $\mu $
and
$\mu $
and
![]() $ \lambda $
are strict partitions, then
$ \lambda $
are strict partitions, then
![]() $ j\hspace {-0.1mm}q_{\lambda /\mu }=j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
.
$ j\hspace {-0.1mm}q_{\lambda /\mu }=j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
.
Proof. We first claim that if
![]() $n>0$
, then
$n>0$
, then
![]() $ j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda j\hspace {-0.1mm}q^{\mathrm {comb}}_n = \sum _\nu \widehat b^{\nu }_{\lambda ,(n)} \beta ^{|\lambda |-|\nu |+n} j\hspace {-0.1mm}q^{\mathrm {comb}}_\nu $
, where the sum is over all strict partitions
$ j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda j\hspace {-0.1mm}q^{\mathrm {comb}}_n = \sum _\nu \widehat b^{\nu }_{\lambda ,(n)} \beta ^{|\lambda |-|\nu |+n} j\hspace {-0.1mm}q^{\mathrm {comb}}_\nu $
, where the sum is over all strict partitions
![]() $\nu $
. This holds if
$\nu $
. This holds if
![]() $\lambda = \emptyset $
since
$\lambda = \emptyset $
since
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda =1$
and it is clear from Proposition 2.7 that
$j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda =1$
and it is clear from Proposition 2.7 that
![]() $\widehat b^{(n)}_{\emptyset ,(n)} =1$
and
$\widehat b^{(n)}_{\emptyset ,(n)} =1$
and
![]() $\widehat b^{\nu }_{\emptyset ,(n)} =0$
for
$\widehat b^{\nu }_{\emptyset ,(n)} =0$
for
![]() $\nu \neq (n)$
. If
$\nu \neq (n)$
. If
![]() $\lambda $
is nonempty, then the desired formula follows by substituting Lemmas 4.9 and 4.12 with
$\lambda $
is nonempty, then the desired formula follows by substituting Lemmas 4.9 and 4.12 with
![]() $\Lambda := (n+\lambda _1,\lambda _1,\lambda _2,\dots )$
into Corollary 4.5.
$\Lambda := (n+\lambda _1,\lambda _1,\lambda _2,\dots )$
into Corollary 4.5.
Let
![]() $\prec $
be the total order on strict partitions with
$\prec $
be the total order on strict partitions with
![]() $\mu \prec \lambda $
if
$\mu \prec \lambda $
if
![]() $\mu \neq \lambda $
and either
$\mu \neq \lambda $
and either
![]() $|\mu | < |\lambda |$
or
$|\mu | < |\lambda |$
or
![]() $|\mu | = |\lambda |$
and the first index i with
$|\mu | = |\lambda |$
and the first index i with
![]() $\mu _i \neq \lambda _i$
has
$\mu _i \neq \lambda _i$
has
![]() $\mu _i> \lambda _i$
. Suppose
$\mu _i> \lambda _i$
. Suppose
![]() $\lambda $
is a strict partition with
$\lambda $
is a strict partition with
![]() $k>0$
nonzero parts. Let
$k>0$
nonzero parts. Let
![]() $\mu := (\lambda _1,\lambda _2,\dots ,\lambda _{k-1})$
and
$\mu := (\lambda _1,\lambda _2,\dots ,\lambda _{k-1})$
and
![]() $n =\lambda _k$
. Then it follows from Proposition 2.7 that
$n =\lambda _k$
. Then it follows from Proposition 2.7 that
so we can write
The same formula holds with each ‘
![]() $j\hspace {-0.1mm}q$
’ replaced by ‘
$j\hspace {-0.1mm}q$
’ replaced by ‘
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}$
’ in view of the previous paragraph. Since
$j\hspace {-0.1mm}q^{\mathrm {comb}}$
’ in view of the previous paragraph. Since
![]() $j\hspace {-0.1mm}q_n=j\hspace {-0.1mm}q^{\mathrm {comb}}_n$
for all integers
$j\hspace {-0.1mm}q_n=j\hspace {-0.1mm}q^{\mathrm {comb}}_n$
for all integers
![]() $n\geq 0$
by Proposition 4.1, it follows by induction that
$n\geq 0$
by Proposition 4.1, it follows by induction that
![]() $j\hspace {-0.1mm}q_\lambda =j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda $
.
$j\hspace {-0.1mm}q_\lambda =j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda $
.
The last thing to explain is how to generalize this identity to
![]() $j\hspace {-0.1mm}q_{\lambda /\mu }=j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
. As the power series
$j\hspace {-0.1mm}q_{\lambda /\mu }=j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
. As the power series
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda $
is symmetric, it is clear from its definition that
$j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda $
is symmetric, it is clear from its definition that
![]() $ j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda (\mathbf {x},\mathbf {y}) = \sum _{\mu } j\hspace {-0.1mm}q^{\mathrm {comb}}_\mu (\mathbf {x}) j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }(\mathbf {y})$
. Compare this with (2.6). Since
$ j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda (\mathbf {x},\mathbf {y}) = \sum _{\mu } j\hspace {-0.1mm}q^{\mathrm {comb}}_\mu (\mathbf {x}) j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }(\mathbf {y})$
. Compare this with (2.6). Since
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda (\mathbf {x},\mathbf {y}) = j\hspace {-0.1mm}q_\lambda (\mathbf {x},\mathbf {y}) $
and since the symmetric functions
$j\hspace {-0.1mm}q^{\mathrm {comb}}_\lambda (\mathbf {x},\mathbf {y}) = j\hspace {-0.1mm}q_\lambda (\mathbf {x},\mathbf {y}) $
and since the symmetric functions
![]() $j\hspace {-0.1mm}q_\mu (\mathbf {x}) = j\hspace {-0.1mm}q^{\mathrm {comb}}_\mu (\mathbf {x}) $
are linearly independent, we must have
$j\hspace {-0.1mm}q_\mu (\mathbf {x}) = j\hspace {-0.1mm}q^{\mathrm {comb}}_\mu (\mathbf {x}) $
are linearly independent, we must have
![]() $j\hspace {-0.1mm}q_{\lambda /\mu }=j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
for all
$j\hspace {-0.1mm}q_{\lambda /\mu }=j\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
for all
![]() $\mu $
.
$\mu $
.
4.4 Bar tableau generating functions without diagonal primes
We turn to our other family
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}$
of bar tableau generating functions. The relevant arguments are similar to those above. Continue to assume that
$j\hspace {-0.1mm}p^{\mathrm {comb}}$
of bar tableau generating functions. The relevant arguments are similar to those above. Continue to assume that
![]() $\Lambda =(\Lambda _1,\Lambda _2,\dots ) \supseteq \Psi \supseteq \Gamma = (\Lambda _2,\Lambda _3,\dots )$
are strict partitions so that
$\Lambda =(\Lambda _1,\Lambda _2,\dots ) \supseteq \Psi \supseteq \Gamma = (\Lambda _2,\Lambda _3,\dots )$
are strict partitions so that
![]() $ \textsf {SD}_{\Lambda /\Psi }$
is a shifted ribbon. We retain the same meaning of a forced box in
$ \textsf {SD}_{\Lambda /\Psi }$
is a shifted ribbon. We retain the same meaning of a forced box in
![]() $\textsf {SD}_{\Lambda /\Psi }$
. We additionally define a position
$\textsf {SD}_{\Lambda /\Psi }$
. We additionally define a position
![]() $(i,j) \in \textsf {SD}_{\Lambda /\Psi }$
to be diagonally-forced if
$(i,j) \in \textsf {SD}_{\Lambda /\Psi }$
to be diagonally-forced if
![]() $i=j$
or if
$i=j$
or if
![]() $(i+1,j) = (j,j) \in \textsf {SD}_{\Lambda /\Psi }$
.
$(i+1,j) = (j,j) \in \textsf {SD}_{\Lambda /\Psi }$
.
Throughout, we fix the meaning of four integer parameters
![]() $\mathsf {sc}^\ast $
,
$\mathsf {sc}^\ast $
,
![]() $\mathsf {mc}^\ast $
,
$\mathsf {mc}^\ast $
,
![]() $\mathsf {fb}^\ast $
,
$\mathsf {fb}^\ast $
,
![]() $\mathsf {res}^\ast $
which are slightly different from the ones
$\mathsf {res}^\ast $
which are slightly different from the ones
![]() $\mathsf {sc}$
,
$\mathsf {sc}$
,
![]() $\mathsf {mc}$
,
$\mathsf {mc}$
,
![]() $\mathsf {fb}$
,
$\mathsf {fb}$
,
![]() $\mathsf {res}$
defined in the previous subsection. Let
$\mathsf {res}$
defined in the previous subsection. Let
![]() $\mathsf {sc}^\ast $
(respectively,
$\mathsf {sc}^\ast $
(respectively,
![]() $\mathsf {mc}^\ast $
) be the number of connected components in
$\mathsf {mc}^\ast $
) be the number of connected components in
![]() $\textsf {SD}_{\Lambda /\Psi }$
that are disjoint from the diagonal that are singleton sets (respectively, have multiple boxes). Let
$\textsf {SD}_{\Lambda /\Psi }$
that are disjoint from the diagonal that are singleton sets (respectively, have multiple boxes). Let
![]() $\mathsf {fb}^\ast $
be the number of forced or diagonally-forced boxes in
$\mathsf {fb}^\ast $
be the number of forced or diagonally-forced boxes in
![]() $\textsf {SD}_{\Lambda /\Psi }$
. Then define
$\textsf {SD}_{\Lambda /\Psi }$
. Then define
![]() $\mathsf {res}^\ast := |\Lambda | - |\Psi | - \mathsf {sc}^\ast - 2\mathsf {mc}^\ast -\mathsf {fb}^\ast +1 \geq 1$
.
$\mathsf {res}^\ast := |\Lambda | - |\Psi | - \mathsf {sc}^\ast - 2\mathsf {mc}^\ast -\mathsf {fb}^\ast +1 \geq 1$
.
Lemma 4.14. With the definitions above, we have
Proof. If
![]() $\textsf {SD}_{\Lambda /\Psi }$
has no diagonal positions, then
$\textsf {SD}_{\Lambda /\Psi }$
has no diagonal positions, then
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }(t) = j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t)$
and
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }(t) = j\hspace {-0.1mm}q^{\mathrm {comb}}_{\Lambda /\Psi }(t)$
and
![]() $\mathsf {sc}=\mathsf {sc}^\ast $
,
$\mathsf {sc}=\mathsf {sc}^\ast $
,
![]() $\mathsf {mc}=\mathsf {mc}^\ast $
,
$\mathsf {mc}=\mathsf {mc}^\ast $
,
![]() $\mathsf {fb}=\mathsf {fb}^\ast $
and
$\mathsf {fb}=\mathsf {fb}^\ast $
and
![]() $\mathsf {res}=\mathsf {res}^\ast +1$
, so the desired formula is equivalent to Lemma 4.7.
$\mathsf {res}=\mathsf {res}^\ast +1$
, so the desired formula is equivalent to Lemma 4.7.
If instead
![]() $\textsf {SD}_{\Lambda /\Psi }$
has just one connected component and this component intersects the diagonal, consider the elements of
$\textsf {SD}_{\Lambda /\Psi }$
has just one connected component and this component intersects the diagonal, consider the elements of
![]() $\mathsf {ShBT}_P(\Psi /\Gamma )$
with all entries in
$\mathsf {ShBT}_P(\Psi /\Gamma )$
with all entries in
![]() $\{1' ,1\}$
. As one reads such a tableau in the row-reading order, each forced box and each diagonally-forced box must start a new bar, while every remaining box is free to either start a new bar or continue the bar of its predecessor. In particular, the first box of
$\{1' ,1\}$
. As one reads such a tableau in the row-reading order, each forced box and each diagonally-forced box must start a new bar, while every remaining box is free to either start a new bar or continue the bar of its predecessor. In particular, the first box of
![]() $\textsf {SD}_{\Lambda /\Psi }$
, which is some diagonal position
$\textsf {SD}_{\Lambda /\Psi }$
, which is some diagonal position
![]() $(j,j)$
, must start a new bar and contain an unprimed entry, and if the second box is the diagonally-forced position
$(j,j)$
, must start a new bar and contain an unprimed entry, and if the second box is the diagonally-forced position
![]() $(j-1,j)$
, then it must contain a primed entry and start a new bar. Comparing these observations with the definition
$(j-1,j)$
, then it must contain a primed entry and start a new bar. Comparing these observations with the definition
![]() $ j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }$
, we see that
$ j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }$
, we see that
![]() $ j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }(t) = t^{\mathsf {fb}^\ast } (t-\beta )^{|\Lambda |-|\Psi | - \mathsf {fb}^\ast }$
, which is equivalent to the desired formula since in this special case,
$ j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }(t) = t^{\mathsf {fb}^\ast } (t-\beta )^{|\Lambda |-|\Psi | - \mathsf {fb}^\ast }$
, which is equivalent to the desired formula since in this special case,
![]() $\mathsf {sc}^\ast =\mathsf {mc}^\ast =0$
and
$\mathsf {sc}^\ast =\mathsf {mc}^\ast =0$
and
![]() $\mathsf {res}^\ast = |\Lambda |-|\Psi |-\mathsf {fb}^\ast + 1$
.
$\mathsf {res}^\ast = |\Lambda |-|\Psi |-\mathsf {fb}^\ast + 1$
.
When not in these cases,
![]() $\textsf {SD}_{\Lambda /\Psi } = \textsf {SD}_{\Lambda ^1/\Psi ^1}\sqcup \textsf {SD}_{\Lambda ^2/\Psi ^2}$
for some strict partitions
$\textsf {SD}_{\Lambda /\Psi } = \textsf {SD}_{\Lambda ^1/\Psi ^1}\sqcup \textsf {SD}_{\Lambda ^2/\Psi ^2}$
for some strict partitions
![]() $\Psi ^i\subsetneq \Lambda ^i$
such that
$\Psi ^i\subsetneq \Lambda ^i$
such that
![]() $\textsf {SD}_{\Lambda ^1/\Psi ^1}$
has no diagonal boxes and
$\textsf {SD}_{\Lambda ^1/\Psi ^1}$
has no diagonal boxes and
![]() $\textsf {SD}_{\Lambda ^2/\Psi ^2}$
has just one connected component which intersects the diagonal and is not adjacent to any box in
$\textsf {SD}_{\Lambda ^2/\Psi ^2}$
has just one connected component which intersects the diagonal and is not adjacent to any box in
![]() $\textsf {SD}_{\Lambda ^1/\Psi ^1}$
. Then
$\textsf {SD}_{\Lambda ^1/\Psi ^1}$
. Then
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }(t) = j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda ^1/\Psi ^1}(t) j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda ^2/\Psi ^2}(t)$
, where
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /\Psi }(t) = j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda ^1/\Psi ^1}(t) j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda ^2/\Psi ^2}(t)$
, where
for integers with
![]() $\mathsf {sc}^\ast =\mathsf {sc}^\ast _1+\mathsf {sc}^\ast _2$
,
$\mathsf {sc}^\ast =\mathsf {sc}^\ast _1+\mathsf {sc}^\ast _2$
,
![]() $\mathsf {mc}^\ast =\mathsf {mc}^\ast _1+\mathsf {mc}^\ast _2$
,
$\mathsf {mc}^\ast =\mathsf {mc}^\ast _1+\mathsf {mc}^\ast _2$
,
![]() $\mathsf {fb}^\ast =\mathsf {fb}^\ast _1+\mathsf {fb}^\ast _2$
and
$\mathsf {fb}^\ast =\mathsf {fb}^\ast _1+\mathsf {fb}^\ast _2$
and
![]() $\mathsf {res}^\ast = \mathsf {res}^\ast _1 + \mathsf {res}^\ast _2 - 1$
, which suffices.
$\mathsf {res}^\ast = \mathsf {res}^\ast _1 + \mathsf {res}^\ast _2 - 1$
, which suffices.
Since
![]() $\{j\hspace {-0.1mm}p^{\mathrm {comb}}_n(t): n\geq 0\}$
is a homogeneous
$\{j\hspace {-0.1mm}p^{\mathrm {comb}}_n(t): n\geq 0\}$
is a homogeneous
![]() $\mathbb {Z}[\beta ]$
-basis for
$\mathbb {Z}[\beta ]$
-basis for
![]() $\mathbb {Z}[\beta ,t]$
, we can write
$\mathbb {Z}[\beta ,t]$
, we can write
for unique numbers
![]() $ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} \in \mathbb {Z}$
.
$ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} \in \mathbb {Z}$
.
Corollary 4.15. The coefficients
![]() $ \mathfrak {c}^{\Lambda }_{\Psi ,(n)}$
are nonnegative integers with these properties:
$ \mathfrak {c}^{\Lambda }_{\Psi ,(n)}$
are nonnegative integers with these properties:
-
(a) If
 $n = 0 < |\Lambda |-|\Psi |$
or
$n = 0 < |\Lambda |-|\Psi |$
or
 $n> |\Lambda |-|\Psi |$
, then
$n> |\Lambda |-|\Psi |$
, then
 $ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 0$
.
$ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 0$
. -
(b) If
 $0 < n = |\Lambda | - |\Psi |$
, then
$0 < n = |\Lambda | - |\Psi |$
, then
 $ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 2^{ \mathsf {sc}^\ast +\mathsf {mc}^\ast }$
.
$ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 2^{ \mathsf {sc}^\ast +\mathsf {mc}^\ast }$
. -
(c) If
 $0 < n = |\Lambda | - |\Psi | - 1$
, then
$0 < n = |\Lambda | - |\Psi | - 1$
, then
 $ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 2^{\mathsf {sc}^\ast +\mathsf {mc}^\ast -1}(2\mathsf {sc}^\ast +3\mathsf {mc}^\ast +2\mathsf {fb}^\ast -2)$
.
$ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 2^{\mathsf {sc}^\ast +\mathsf {mc}^\ast -1}(2\mathsf {sc}^\ast +3\mathsf {mc}^\ast +2\mathsf {fb}^\ast -2)$
.
Proof. The argument is similar to the proof of Corollary 4.8 and follows as a simple exercise in algebra from Proposition 4.6 and Lemma 4.14. We omit the details.
Lemma 4.16. If
![]() $0 \leq n \leq \Lambda _1$
is an integer, then
$0 \leq n \leq \Lambda _1$
is an integer, then
 $\displaystyle j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /(n)} = \sum _{\substack {\mu \text { strict} \\ \Gamma \subseteq \mu \subseteq \Lambda }} \mathfrak {c}^{\Lambda }_{\mu ,(n)} \cdot \beta ^{|\Lambda |-|\mu |-n}\cdot j\hspace {-0.1mm}p^{\mathrm {comb}}_\mu. $
$\displaystyle j\hspace {-0.1mm}p^{\mathrm {comb}}_{\Lambda /(n)} = \sum _{\substack {\mu \text { strict} \\ \Gamma \subseteq \mu \subseteq \Lambda }} \mathfrak {c}^{\Lambda }_{\mu ,(n)} \cdot \beta ^{|\Lambda |-|\mu |-n}\cdot j\hspace {-0.1mm}p^{\mathrm {comb}}_\mu. $
Proof. Repeat the proof of Lemma 4.9, replacing ‘
![]() $j\hspace {-0.1mm}q^{\mathrm {comb}}$
’ by ‘
$j\hspace {-0.1mm}q^{\mathrm {comb}}$
’ by ‘
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}$
’ and ‘
$j\hspace {-0.1mm}p^{\mathrm {comb}}$
’ and ‘
![]() $\mathfrak {b}$
’ by ‘
$\mathfrak {b}$
’ by ‘
![]() $\mathfrak {c}$
’.
$\mathfrak {c}$
’.
Consider the set of removable corner boxes
![]() $(i,j) \in \textsf {SD}_\Gamma $
with
$(i,j) \in \textsf {SD}_\Gamma $
with
![]() $(i+1,j+1) \notin \textsf {SD}_{\Psi /\Gamma }$
. Let
$(i+1,j+1) \notin \textsf {SD}_{\Psi /\Gamma }$
. Let
![]() $\mathcal {U}^\ast $
,
$\mathcal {U}^\ast $
,
![]() ${\mathcal {V}}^\ast $
and
${\mathcal {V}}^\ast $
and
![]() ${\mathcal {W}}^\ast $
be the sets of such corners
${\mathcal {W}}^\ast $
be the sets of such corners
![]() $(i,j)$
for which the size of
$(i,j)$
for which the size of
![]() $\{(i,j+1),(i+1,j)\} \cap \textsf {SD}_{\Psi /\Gamma }$
is exactly two, one or zero, respectively. The union
$\{(i,j+1),(i+1,j)\} \cap \textsf {SD}_{\Psi /\Gamma }$
is exactly two, one or zero, respectively. The union
![]() $\mathcal {U}^\ast \sqcup {\mathcal {V}}^\ast \sqcup {\mathcal {W}}^\ast $
of these three sets is the same as the union of
$\mathcal {U}^\ast \sqcup {\mathcal {V}}^\ast \sqcup {\mathcal {W}}^\ast $
of these three sets is the same as the union of
![]() $\mathcal {U} \sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
of the sets defined before Lemma 4.10.
$\mathcal {U} \sqcup {\mathcal {V}} \sqcup {\mathcal {W}}$
of the sets defined before Lemma 4.10.
Lemma 4.17. Suppose
![]() $\Lambda _1 - \Psi _1 \geq 2$
. Then
$\Lambda _1 - \Psi _1 \geq 2$
. Then
![]() $ |\mathcal {U}^\ast | = \mathsf {sc}^\ast $
and
$ |\mathcal {U}^\ast | = \mathsf {sc}^\ast $
and
![]() $ |{\mathcal {V}}^\ast | + 2|{\mathcal {W}}^\ast | = \mathsf {mc}^\ast +\mathsf {fb}^\ast -1$
.
$ |{\mathcal {V}}^\ast | + 2|{\mathcal {W}}^\ast | = \mathsf {mc}^\ast +\mathsf {fb}^\ast -1$
.
Proof. Let
![]() $(i,i)$
be the unique diagonal position in
$(i,i)$
be the unique diagonal position in
![]() $\textsf {SD}_{\Lambda /\Gamma }$
. If this box is in
$\textsf {SD}_{\Lambda /\Gamma }$
. If this box is in
![]() $\textsf {SD}_{\Psi /\Gamma }$
rather than
$\textsf {SD}_{\Psi /\Gamma }$
rather than
![]() $\textsf {SD}_{\Lambda /\Psi }$
, then
$\textsf {SD}_{\Lambda /\Psi }$
, then
![]() $\mathcal {U}=\mathcal {U}^\ast $
,
$\mathcal {U}=\mathcal {U}^\ast $
,
![]() ${\mathcal {V}}={\mathcal {V}}^\ast $
and
${\mathcal {V}}={\mathcal {V}}^\ast $
and
![]() ${\mathcal {W}} = {\mathcal {W}}^\ast $
along with
${\mathcal {W}} = {\mathcal {W}}^\ast $
along with
![]() $\mathsf {sc}=\mathsf {sc}^\ast $
,
$\mathsf {sc}=\mathsf {sc}^\ast $
,
![]() $\mathsf {mc}=\mathsf {mc}^\ast $
and
$\mathsf {mc}=\mathsf {mc}^\ast $
and
![]() $\mathsf {fb}=\mathsf {fb}^\ast $
, so the desired properties hold by Lemma 4.10. If box
$\mathsf {fb}=\mathsf {fb}^\ast $
, so the desired properties hold by Lemma 4.10. If box
![]() $(i,i)$
belongs to
$(i,i)$
belongs to
![]() $\textsf {SD}_{\Lambda /\Psi }$
but is not adjacent to any other box in
$\textsf {SD}_{\Lambda /\Psi }$
but is not adjacent to any other box in
![]() $\textsf {SD}_{\Lambda /\Psi }$
, then we cannot have
$\textsf {SD}_{\Lambda /\Psi }$
, then we cannot have
![]() $(i,i+1) \in \textsf {SD}_{\Lambda /\Gamma }$
, so it must hold that
$(i,i+1) \in \textsf {SD}_{\Lambda /\Gamma }$
, so it must hold that
![]() $(i-1,i) \in \textsf {SD}_{\Psi /\Gamma }$
, which means that
$(i-1,i) \in \textsf {SD}_{\Psi /\Gamma }$
, which means that
![]() $\mathcal {U} = \mathcal {U}^\ast \sqcup \{(i-1,i-1)\} $
and
$\mathcal {U} = \mathcal {U}^\ast \sqcup \{(i-1,i-1)\} $
and
![]() $ {\mathcal {V}}^\ast = {\mathcal {V}} \sqcup \{(i-1,i-1)\}$
, and therefore
$ {\mathcal {V}}^\ast = {\mathcal {V}} \sqcup \{(i-1,i-1)\}$
, and therefore
along with
Suppose finally that box
![]() $(i,i)$
belongs to a connected component of
$(i,i)$
belongs to a connected component of
![]() $\textsf {SD}_{\Lambda /\Psi }$
with multiple boxes. Similar to our reasoning above, if the second box of
$\textsf {SD}_{\Lambda /\Psi }$
with multiple boxes. Similar to our reasoning above, if the second box of
![]() $\textsf {SD}_{\Lambda /\Psi }$
is
$\textsf {SD}_{\Lambda /\Psi }$
is
![]() $(i,i+1)$
, then we have
$(i,i+1)$
, then we have
along with
while if the second box of
![]() $\textsf {SD}_{\Lambda /\Psi }$
is
$\textsf {SD}_{\Lambda /\Psi }$
is
![]() $(i-1,i)$
, then we have
$(i-1,i)$
, then we have
along with
In each of these cases, the desired identities follow by Lemma 4.10.
Lemma 4.18. If
![]() $\Lambda _1 - \Psi _1 \geq 2$
, then
$\Lambda _1 - \Psi _1 \geq 2$
, then
Proof. By Proposition 2.7, the number
![]() $ \widehat c^\Psi _{\Gamma ,(n)}$
counts the ways that we can add a subset of removable corner boxes of
$ \widehat c^\Psi _{\Gamma ,(n)}$
counts the ways that we can add a subset of removable corner boxes of
![]() $\textsf {SD}_\Gamma $
to
$\textsf {SD}_\Gamma $
to
![]() $\textsf {SD}_{\Psi /\Gamma }$
to form a shifted ribbon, and then assign either
$\textsf {SD}_{\Psi /\Gamma }$
to form a shifted ribbon, and then assign either
![]() $1$
or
$1$
or
![]() $1'$
or
$1'$
or
![]() $1'1$
to the first box in each connected component of this ribbon, such that the number of boxes plus the number of entries equal to
$1'1$
to the first box in each connected component of this ribbon, such that the number of boxes plus the number of entries equal to
![]() $1'1$
is n. As in the proof of Lemma 4.11, the shifted ribbons that arise in this way are the unions of
$1'1$
is n. As in the proof of Lemma 4.11, the shifted ribbons that arise in this way are the unions of
![]() $\textsf {SD}_{\Psi /\Gamma }$
with arbitrary subsets of
$\textsf {SD}_{\Psi /\Gamma }$
with arbitrary subsets of
![]() $\mathcal {U}^\ast \sqcup {\mathcal {V}}^\ast \sqcup {\mathcal {W}}^\ast $
. The ribbon
$\mathcal {U}^\ast \sqcup {\mathcal {V}}^\ast \sqcup {\mathcal {W}}^\ast $
. The ribbon
![]() $\textsf {SD}_{\Psi /\Gamma }$
starts out with
$\textsf {SD}_{\Psi /\Gamma }$
starts out with
![]() $\mathsf {sc}^\ast +\mathsf {mc}^\ast $
connected components, and each box added from
$\mathsf {sc}^\ast +\mathsf {mc}^\ast $
connected components, and each box added from
![]() $\mathcal {U}^\ast $
,
$\mathcal {U}^\ast $
,
![]() $ {\mathcal {V}}^\ast $
and
$ {\mathcal {V}}^\ast $
and
![]() $ {\mathcal {W}}^\ast $
respectively adds
$ {\mathcal {W}}^\ast $
respectively adds
![]() $-1$
,
$-1$
,
![]() $0$
and
$0$
and
![]() $1$
to this number. Combining these observations with Lemma 4.17, we deduce that
$1$
to this number. Combining these observations with Lemma 4.17, we deduce that
 $$\begin{align*}\begin{aligned} \sum_{n \geq 0} \widehat c^\Psi_{\Gamma,(n)} u^{n } &= u ^{|\Psi|-|\Gamma|}(2 + u)^{\mathsf{sc}^\ast+\mathsf{mc}^\ast}(1 + \tfrac{u}{2+u})^{|\mathcal{U}^\ast|}(1+u)^{|{\mathcal{V}}^\ast|} (1 + u(2+u))^{|{\mathcal{W}}^\ast|} \\& = 2^{\mathsf{sc}^\ast} u ^{|\Psi|-|\Gamma|} (2+u)^{\mathsf{mc}^\ast} (1+u)^{\mathsf{sc}^\ast+\mathsf{mc}^\ast+\mathsf{fb}^\ast-1}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \sum_{n \geq 0} \widehat c^\Psi_{\Gamma,(n)} u^{n } &= u ^{|\Psi|-|\Gamma|}(2 + u)^{\mathsf{sc}^\ast+\mathsf{mc}^\ast}(1 + \tfrac{u}{2+u})^{|\mathcal{U}^\ast|}(1+u)^{|{\mathcal{V}}^\ast|} (1 + u(2+u))^{|{\mathcal{W}}^\ast|} \\& = 2^{\mathsf{sc}^\ast} u ^{|\Psi|-|\Gamma|} (2+u)^{\mathsf{mc}^\ast} (1+u)^{\mathsf{sc}^\ast+\mathsf{mc}^\ast+\mathsf{fb}^\ast-1}. \end{aligned}\end{align*}$$
This becomes the desired identity after dividing both sides by
![]() $u ^{|\Psi |-|\Gamma |}$
, replacing u by
$u ^{|\Psi |-|\Gamma |}$
, replacing u by
![]() $\beta u^{-1}$
, and then multiplying both sides by
$\beta u^{-1}$
, and then multiplying both sides by
![]() $u^{\mathsf {sc}^\ast +2\mathsf {mc}^\ast +\mathsf {fb}^\ast -1} = u^{|\Lambda |-|\Psi |-\mathsf {res}^\ast } =u^{\Lambda _1-\mathsf {res}^\ast + |\Gamma |-|\Psi | }$
.
$u^{\mathsf {sc}^\ast +2\mathsf {mc}^\ast +\mathsf {fb}^\ast -1} = u^{|\Lambda |-|\Psi |-\mathsf {res}^\ast } =u^{\Lambda _1-\mathsf {res}^\ast + |\Gamma |-|\Psi | }$
.
Lemma 4.19. If
![]() $n = \Lambda _1 - \Lambda _2$
and
$n = \Lambda _1 - \Lambda _2$
and
![]() $m=\Lambda _2>0$
, then
$m=\Lambda _2>0$
, then
 $$\begin{align*}\widehat c^\Psi_{\Gamma,(n)} - \mathfrak{c}^{\Lambda}_{\Psi,(m)} = \begin{cases} 1 &\text{if }\Psi = (\Lambda_1,\Lambda_3,\Lambda_4,\dots)\\ 1 &\text{if }\Psi = (\Lambda_1-1,\Lambda_3,\Lambda_4,\dots) \\ 0&\text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\widehat c^\Psi_{\Gamma,(n)} - \mathfrak{c}^{\Lambda}_{\Psi,(m)} = \begin{cases} 1 &\text{if }\Psi = (\Lambda_1,\Lambda_3,\Lambda_4,\dots)\\ 1 &\text{if }\Psi = (\Lambda_1-1,\Lambda_3,\Lambda_4,\dots) \\ 0&\text{otherwise}. \end{cases}\end{align*}$$
Proof. As in the proof of Lemma 4.12, if
![]() $\Lambda _1-\Psi _1 \geq 2$
and
$\Lambda _1-\Psi _1 \geq 2$
and
![]() $n+m=\Lambda _1$
, then it follows from Proposition 4.6 and Lemmas 4.14 and 4.18 that
$n+m=\Lambda _1$
, then it follows from Proposition 4.6 and Lemmas 4.14 and 4.18 that
![]() $\widehat c^\Psi _{\Gamma ,(n)}$
and
$\widehat c^\Psi _{\Gamma ,(n)}$
and
![]() $ \mathfrak {c}^{\Lambda }_{\Psi ,(m)} $
are both equal to the coefficient of
$ \mathfrak {c}^{\Lambda }_{\Psi ,(m)} $
are both equal to the coefficient of
![]() $\beta ^{|\Lambda |-|\Psi | -m} u^{m-\mathsf {res}^\ast }$
in
$\beta ^{|\Lambda |-|\Psi | -m} u^{m-\mathsf {res}^\ast }$
in
![]() $2^{\mathsf {sc}^\ast } (u+\beta )^{\mathsf {sc}^\ast +\mathsf {mc}^\ast +\mathsf {fb}^\ast -1} (2u +\beta )^{\mathsf {mc}^\ast } $
.
$2^{\mathsf {sc}^\ast } (u+\beta )^{\mathsf {sc}^\ast +\mathsf {mc}^\ast +\mathsf {fb}^\ast -1} (2u +\beta )^{\mathsf {mc}^\ast } $
.
To handle the cases when
![]() $\Lambda _1-\Psi _1 \in \{0,1\}$
, we fix
$\Lambda _1-\Psi _1 \in \{0,1\}$
, we fix
![]() $n=\Lambda _1-\Lambda _2$
and
$n=\Lambda _1-\Lambda _2$
and
![]() $m=\Lambda _2>0$
; in particular,
$m=\Lambda _2>0$
; in particular,
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Gamma $
are both nonempty. If
$\Gamma $
are both nonempty. If
![]() $|\Psi |-|\Gamma |>n$
, then
$|\Psi |-|\Gamma |>n$
, then
![]() $|\Lambda |-|\Psi | < m$
and it follows from Proposition 2.7 and Corollary 4.15 that
$|\Lambda |-|\Psi | < m$
and it follows from Proposition 2.7 and Corollary 4.15 that
![]() $\widehat c^\Psi _{\Gamma ,(n)} = \mathfrak {c}^{\Lambda }_{\Psi ,(m)} = 0$
, as desired. We may therefore assume
$\widehat c^\Psi _{\Gamma ,(n)} = \mathfrak {c}^{\Lambda }_{\Psi ,(m)} = 0$
, as desired. We may therefore assume
![]() $|\Psi |-|\Gamma |\leq n$
. There are three main cases, which are similar to the ones in the proof of Lemma 4.12:
$|\Psi |-|\Gamma |\leq n$
. There are three main cases, which are similar to the ones in the proof of Lemma 4.12:
-
(1) If
 $\Lambda _1=\Psi _1$
, then
$\Lambda _1=\Psi _1$
, then
 $\Psi = (\Lambda _1,\Lambda _3,\Lambda _4,\dots )= \Gamma + (n,0,0,\dots )$
as in case (1) of the proof of Lemma 4.12. Then
$\Psi = (\Lambda _1,\Lambda _3,\Lambda _4,\dots )= \Gamma + (n,0,0,\dots )$
as in case (1) of the proof of Lemma 4.12. Then
 $\mathsf {sc}^\ast =\mathsf {mc}^\ast =0$
so
$\mathsf {sc}^\ast =\mathsf {mc}^\ast =0$
so
 $ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 2^{\mathsf {sc}^\ast +\mathsf {mc}^\ast }=1$
by Corollary 4.15, and since
$ \mathfrak {c}^{\Lambda }_{\Psi ,(n)} = 2^{\mathsf {sc}^\ast +\mathsf {mc}^\ast }=1$
by Corollary 4.15, and since
 $\Gamma $
is nonempty, one has
$\Gamma $
is nonempty, one has
 $\widehat c^\Psi _{\Gamma ,(n)} = \widehat b^\Psi _{\Gamma ,(n)}=2$
by Proposition 2.7, so
$\widehat c^\Psi _{\Gamma ,(n)} = \widehat b^\Psi _{\Gamma ,(n)}=2$
by Proposition 2.7, so
 $\widehat c^\Psi _{\Gamma ,(n)} - \mathfrak {c}^{\Lambda }_{\Psi ,(m)}=1 $
, as claimed.
$\widehat c^\Psi _{\Gamma ,(n)} - \mathfrak {c}^{\Lambda }_{\Psi ,(m)}=1 $
, as claimed. -
(2) If
 $\Lambda _1-\Psi _1=1$
, then
$\Lambda _1-\Psi _1=1$
, then
 $|\Psi |-|\Gamma | \in \{n-1,n\}$
as in case (2) of the proof of Lemma 4.12. If we also have
$|\Psi |-|\Gamma | \in \{n-1,n\}$
as in case (2) of the proof of Lemma 4.12. If we also have
 $|\Psi |-|\Gamma | = n$
, then
$|\Psi |-|\Gamma | = n$
, then
 $\textsf {SD}_{\Psi /\Gamma }$
must again consist of the
$\textsf {SD}_{\Psi /\Gamma }$
must again consist of the
 $n-1$
boxes
$n-1$
boxes
 $(1,j) $
with
$(1,j) $
with
 $ \Lambda _2 < j < \Lambda _1$
along with one additional box
$ \Lambda _2 < j < \Lambda _1$
along with one additional box
 $(i,j) \in \textsf {SD}_{\Lambda /\Gamma }$
with
$(i,j) \in \textsf {SD}_{\Lambda /\Gamma }$
with
 $i>1$
. In this case,
$i>1$
. In this case,
 $ \mathfrak {c}^{\Lambda }_{\Psi ,(m)} = 2^{\mathsf {sc}^\ast +\mathsf {mc}^\ast }$
by Corollary 4.15 while
$ \mathfrak {c}^{\Lambda }_{\Psi ,(m)} = 2^{\mathsf {sc}^\ast +\mathsf {mc}^\ast }$
by Corollary 4.15 while
 $\widehat c^\Psi _{\Gamma ,(n)}=2^E$
, where
$\widehat c^\Psi _{\Gamma ,(n)}=2^E$
, where
 $E \in \{1,2\} $
is the number of connected components in
$E \in \{1,2\} $
is the number of connected components in
 $\textsf {SD}_{\Psi /\Gamma }$
by Proposition 2.7. We have
$\textsf {SD}_{\Psi /\Gamma }$
by Proposition 2.7. We have
 $\mathsf {sc}^\ast +\mathsf {mc}^\ast = E$
so
$\mathsf {sc}^\ast +\mathsf {mc}^\ast = E$
so
 $\widehat c^\Psi _{\Gamma ,(n)} = \mathfrak {c}^{\Lambda }_{\Psi ,(m)} $
, as needed.
$\widehat c^\Psi _{\Gamma ,(n)} = \mathfrak {c}^{\Lambda }_{\Psi ,(m)} $
, as needed. -
(3) Finally, if
 $\Lambda _1 - \Psi _1 = 1$
and
$\Lambda _1 - \Psi _1 = 1$
and
 $|\Psi | - |\Gamma | =n-1$
, then as in case (3) of the proof of Lemma 4.12, we must have
$|\Psi | - |\Gamma | =n-1$
, then as in case (3) of the proof of Lemma 4.12, we must have
 $\Psi = (\Lambda _1-1,\Lambda _3,\Lambda _4,\dots ) = \Gamma + (n-1,0,0,\dots )$
. There are now only two subcases:
$\Psi = (\Lambda _1-1,\Lambda _3,\Lambda _4,\dots ) = \Gamma + (n-1,0,0,\dots )$
. There are now only two subcases:-
• If
 $n=1$
, then
$n=1$
, then
 $\Psi =\Gamma $
, so
$\Psi =\Gamma $
, so
 $\mathsf {sc}^\ast =\mathsf {mc}^\ast =0$
and
$\mathsf {sc}^\ast =\mathsf {mc}^\ast =0$
and  $$\begin{align*}\mathfrak{c}^{\Lambda}_{\Psi,(m)}=2^{\mathsf{sc}^\ast+\mathsf{mc}^\ast-1}(2\mathsf{sc}^\ast+3\mathsf{mc}^\ast+2\mathsf{fb}^\ast-2)=\mathsf{fb}^\ast-1\end{align*}$$
$$\begin{align*}\mathfrak{c}^{\Lambda}_{\Psi,(m)}=2^{\mathsf{sc}^\ast+\mathsf{mc}^\ast-1}(2\mathsf{sc}^\ast+3\mathsf{mc}^\ast+2\mathsf{fb}^\ast-2)=\mathsf{fb}^\ast-1\end{align*}$$
by Corollary 4.15, while Proposition 2.7 tells us that
 $\widehat c^\Psi _{\Gamma ,(n)}=2G$
, where
$\widehat c^\Psi _{\Gamma ,(n)}=2G$
, where
 $G>0$
is the number of removable corner boxes of
$G>0$
is the number of removable corner boxes of
 $\textsf {SD}_\Gamma $
. One checks that
$\textsf {SD}_\Gamma $
. One checks that
 $\mathsf {fb}^\ast =2G$
, as illustrated in Figure 6.
$\mathsf {fb}^\ast =2G$
, as illustrated in Figure 6.
Figure 6 Case (3) in the proof of Lemma 4.19: the subcase when
 $n = 1$
,
$n = 1$
,
 $\Psi = \Gamma $
. Forced boxes in
$\Psi = \Gamma $
. Forced boxes in
 $\textsf {SD}_{\Lambda / \Psi }$
are denoted by
$\textsf {SD}_{\Lambda / \Psi }$
are denoted by
 $\bullet $
, diagonally-forced boxes are denoted by
$\bullet $
, diagonally-forced boxes are denoted by
 $\cdot $
, and removable corners of
$\cdot $
, and removable corners of
 $\textsf {SD}_{\Gamma }$
are denoted by
$\textsf {SD}_{\Gamma }$
are denoted by
 $\times $
.
$\times $
. -
• If
 $n>1$
, then
$n>1$
, then
 $\mathsf {sc}^\ast =1$
and
$\mathsf {sc}^\ast =1$
and
 $\mathsf {mc}^\ast =0$
so
$\mathsf {mc}^\ast =0$
so  $$\begin{align*}\mathfrak{b}^{\Lambda}_{\Psi,(m)} =2^{\mathsf{sc}^\ast+\mathsf{mc}^\ast-1}(2\mathsf{sc}^\ast+3\mathsf{mc}^\ast+2\mathsf{fb}^\ast-2)= 2\mathsf{fb}^\ast\end{align*}$$
$$\begin{align*}\mathfrak{b}^{\Lambda}_{\Psi,(m)} =2^{\mathsf{sc}^\ast+\mathsf{mc}^\ast-1}(2\mathsf{sc}^\ast+3\mathsf{mc}^\ast+2\mathsf{fb}^\ast-2)= 2\mathsf{fb}^\ast\end{align*}$$
by Corollary 4.15. But in this case, Proposition 2.7 implies that
 $$\begin{align*}\widehat c^\Psi_{\Gamma,(n)} = 1 + 2J + 4K,\end{align*}$$
$$\begin{align*}\widehat c^\Psi_{\Gamma,(n)} = 1 + 2J + 4K,\end{align*}$$
where
 $J\in \{0,1\}$
and
$J\in \{0,1\}$
and
 $K\geq 0$
are the numbers of removable corner boxes of
$K\geq 0$
are the numbers of removable corner boxes of
 $\textsf {SD}_\Gamma $
which are in or not in the first row. One checks that
$\textsf {SD}_\Gamma $
which are in or not in the first row. One checks that
 $\mathsf {fb}^\ast =J+2K$
as needed.
$\mathsf {fb}^\ast =J+2K$
as needed.
Figure 7 Case (3) in the proof of Lemma 4.19: the subcase when
 $n> 1$
. Left column
$n> 1$
. Left column
 $J = 0$
, right column
$J = 0$
, right column
 $J = 1$
. The blue cells represent
$J = 1$
. The blue cells represent
 $\Psi / \Gamma $
.
$\Psi / \Gamma $
.
In each subcase, we have
 $ \widehat c^\Psi _{\Gamma ,(n)} - \mathfrak {c}^{\Lambda }_{\Psi ,(m)}=1$
, as desired.
$ \widehat c^\Psi _{\Gamma ,(n)} - \mathfrak {c}^{\Lambda }_{\Psi ,(m)}=1$
, as desired. -
This case analysis concludes the proof.
We now arrive at our second main theorem.
Theorem 4.20. If
![]() $\mu $
and
$\mu $
and
![]() $ \lambda $
are strict partitions, then
$ \lambda $
are strict partitions, then
![]() $ j\hspace {-0.1mm}p_{\lambda /\mu }=j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
.
$ j\hspace {-0.1mm}p_{\lambda /\mu }=j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
.
Proof. Our argument has the same structure as the proof of Theorem 4.13. Let
![]() $\prec $
be the total order on strict partitions defined in that proof. Substituting Lemmas 4.16 and 4.19 with
$\prec $
be the total order on strict partitions defined in that proof. Substituting Lemmas 4.16 and 4.19 with
![]() $\Lambda := (n+\lambda _1,\lambda _1,\lambda _2,\dots )$
into Corollary 4.5 shows that
$\Lambda := (n+\lambda _1,\lambda _1,\lambda _2,\dots )$
into Corollary 4.5 shows that
![]() $ j\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda j\hspace {-0.1mm}q^{\mathrm {comb}}_n = \sum _\nu \widehat c^{\nu }_{\lambda ,(n)} \beta ^{|\lambda |-|\nu |+n} j\hspace {-0.1mm}p^{\mathrm {comb}}_\nu $
for all
$ j\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda j\hspace {-0.1mm}q^{\mathrm {comb}}_n = \sum _\nu \widehat c^{\nu }_{\lambda ,(n)} \beta ^{|\lambda |-|\nu |+n} j\hspace {-0.1mm}p^{\mathrm {comb}}_\nu $
for all
![]() $n>0$
. Next, if
$n>0$
. Next, if
![]() $\lambda $
has
$\lambda $
has
![]() $k>0$
nonzero parts,
$k>0$
nonzero parts,
![]() $\mu := (\lambda _1,\lambda _2,\dots ,\lambda _{k-1})$
, and
$\mu := (\lambda _1,\lambda _2,\dots ,\lambda _{k-1})$
, and
![]() $n :=\lambda _k$
, then
$n :=\lambda _k$
, then
by Proposition 2.7, so
 $$\begin{align*}j\hspace{-0.1mm}p_\lambda = \frac{1}{2}j\hspace{-0.1mm}p_{\mu} j\hspace{-0.1mm}q_{n} - \frac{1}{2} \sum_{\nu \prec \lambda} \widehat c^{\nu}_{\mu,(n)} \beta^{|\mu|-|\nu|+n} j\hspace{-0.1mm}p_\nu\end{align*}$$
$$\begin{align*}j\hspace{-0.1mm}p_\lambda = \frac{1}{2}j\hspace{-0.1mm}p_{\mu} j\hspace{-0.1mm}q_{n} - \frac{1}{2} \sum_{\nu \prec \lambda} \widehat c^{\nu}_{\mu,(n)} \beta^{|\mu|-|\nu|+n} j\hspace{-0.1mm}p_\nu\end{align*}$$
and an analogous formula holds for
![]() $j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda } $
. Since
$j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda } $
. Since
![]() $j\hspace {-0.1mm}p_n=j\hspace {-0.1mm}p^{\mathrm {comb}}_n$
and
$j\hspace {-0.1mm}p_n=j\hspace {-0.1mm}p^{\mathrm {comb}}_n$
and
![]() $j\hspace {-0.1mm}q_n=j\hspace {-0.1mm}q^{\mathrm {comb}}_n$
by Proposition 4.1, the identity
$j\hspace {-0.1mm}q_n=j\hspace {-0.1mm}q^{\mathrm {comb}}_n$
by Proposition 4.1, the identity
![]() $j\hspace {-0.1mm}p_\lambda =j\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda $
follows by induction. To deduce that
$j\hspace {-0.1mm}p_\lambda =j\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda $
follows by induction. To deduce that
![]() $j\hspace {-0.1mm}p_{\lambda /\mu }=j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
, one can repeat the last paragraph of the proof of Theorem 4.13 after changing each ‘
$j\hspace {-0.1mm}p_{\lambda /\mu }=j\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
, one can repeat the last paragraph of the proof of Theorem 4.13 after changing each ‘
![]() $j\hspace {-0.1mm}q$
’ to ‘
$j\hspace {-0.1mm}q$
’ to ‘
![]() $j\hspace {-0.1mm}p$
’.
$j\hspace {-0.1mm}p$
’.
4.5 Reverse plane partition generating functions
It remains to show that
![]() $g\hspace {-0.1mm}p_{\lambda /\mu } = g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
and
$g\hspace {-0.1mm}p_{\lambda /\mu } = g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
and
![]() $g\hspace {-0.1mm}q_{\lambda /\mu } = g\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
. Thankfully, we can derive this from Theorems 4.13 and 4.20 by a relatively succinct formal argument.
$g\hspace {-0.1mm}q_{\lambda /\mu } = g\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
. Thankfully, we can derive this from Theorems 4.13 and 4.20 by a relatively succinct formal argument.
Let
![]() $\Lambda $
be the free
$\Lambda $
be the free ![]() -module of linear combinations of strict partitions, and let
-module of linear combinations of strict partitions, and let
![]() $\widehat {\Lambda } $
be the
$\widehat {\Lambda } $
be the ![]() -module of formal (possibly infinite) linear combinations of strict partitions. Write
-module of formal (possibly infinite) linear combinations of strict partitions. Write
![]() $\mathrm {mindeg}(f)$
to denote the smallest degree of any monomial in
$\mathrm {mindeg}(f)$
to denote the smallest degree of any monomial in ![]() , where
, where
![]() $\deg \beta = 0$
and
$\deg \beta = 0$
and
![]() $\deg x_i = 1$
, and set
$\deg x_i = 1$
, and set
![]() $\mathrm {mindeg}(0)=\infty $
. Let
$\mathrm {mindeg}(0)=\infty $
. Let
![]() $\widehat {\Lambda }_{\mathrm {fin}}$
be the submodule of
$\widehat {\Lambda }_{\mathrm {fin}}$
be the submodule of
![]() $\widehat {\Lambda } $
consisting of the elements
$\widehat {\Lambda } $
consisting of the elements
![]() $\sum _\lambda f_\lambda \cdot \lambda $
for which
$\sum _\lambda f_\lambda \cdot \lambda $
for which
![]() $\{ \lambda : \mathrm {mindeg} (f_\lambda ) = n\}$
is finite for all integers n. Then write
$\{ \lambda : \mathrm {mindeg} (f_\lambda ) = n\}$
is finite for all integers n. Then write
for the bilinear form, continuous in the first coordinate, with
![]() $\langle \lambda ,\mu \rangle = \delta _{\lambda \mu }$
for all strict partitions.
$\langle \lambda ,\mu \rangle = \delta _{\lambda \mu }$
for all strict partitions.
Fix an element ![]() with
with
![]() $\mathrm {mindeg}(t)>0$
. Define
$\mathrm {mindeg}(t)>0$
. Define
![]() $\mathcal {P}(t)$
and
$\mathcal {P}(t)$
and
![]() $\mathcal {Q}(t)$
to be the continuous linear maps
$\mathcal {Q}(t)$
to be the continuous linear maps
![]() $\widehat {\Lambda }_{\mathrm {fin}} \to \widehat {\Lambda }_{\mathrm {fin}}$
such that for all strict partitions
$\widehat {\Lambda }_{\mathrm {fin}} \to \widehat {\Lambda }_{\mathrm {fin}}$
such that for all strict partitions
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
, one has
$\lambda $
, one has
Both
![]() $\mathcal {P}(t)$
and
$\mathcal {P}(t)$
and
![]() $\mathcal {Q}(t)$
make sense as maps
$\mathcal {Q}(t)$
make sense as maps
![]() $\widehat {\Lambda } \to \widehat {\Lambda }$
but not as maps
$\widehat {\Lambda } \to \widehat {\Lambda }$
but not as maps
![]() ${\Lambda } \to {\Lambda }$
, since they send any single
${\Lambda } \to {\Lambda }$
, since they send any single
![]() $\mu $
to the infinite sums
$\mu $
to the infinite sums
![]() $\sum _\lambda G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/\mu }(t) \cdot \lambda $
and
$\sum _\lambda G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/\mu }(t) \cdot \lambda $
and
![]() $\sum _\lambda G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\mu }(t)\cdot \lambda $
over all strict partitions
$\sum _\lambda G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\mu }(t)\cdot \lambda $
over all strict partitions
![]() $\lambda \supseteq \mu $
. These operators are well-defined maps
$\lambda \supseteq \mu $
. These operators are well-defined maps
![]() $\widehat {\Lambda }_{\mathrm {fin}}\to \widehat {\Lambda }_{\mathrm {fin}}$
because
$\widehat {\Lambda }_{\mathrm {fin}}\to \widehat {\Lambda }_{\mathrm {fin}}$
because
![]() $\mathrm {mindeg} (G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/\mu }(t))=\mathrm {mindeg} (G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\mu }(t)) = |\lambda /\mu | \cdot \mathrm {mindeg}(t)$
. Similarly, define
$\mathrm {mindeg} (G\hspace {-0.2mm}P_{\lambda /\hspace {-1mm}/\mu }(t))=\mathrm {mindeg} (G\hspace {-0.2mm}Q_{\lambda /\hspace {-1mm}/\mu }(t)) = |\lambda /\mu | \cdot \mathrm {mindeg}(t)$
. Similarly, define
![]() $\mathfrak {p}(t)$
and
$\mathfrak {p}(t)$
and
![]() $\mathfrak {q}(t)$
to be the continuous linear maps
$\mathfrak {q}(t)$
to be the continuous linear maps
![]() $\widehat {\Lambda }_{\mathrm {fin}} \to \widehat {\Lambda }_{\mathrm {fin}}$
with
$\widehat {\Lambda }_{\mathrm {fin}} \to \widehat {\Lambda }_{\mathrm {fin}}$
with
Finally, let
![]() $\tilde {\mathfrak {p}}(t)$
and
$\tilde {\mathfrak {p}}(t)$
and
![]() $\tilde {\mathfrak {q}}(t)$
be the continuous linear maps
$\tilde {\mathfrak {q}}(t)$
be the continuous linear maps
![]() $\widehat {\Lambda }_{\mathrm {fin}} \to \widehat {\Lambda }_{\mathrm {fin}}$
with
$\widehat {\Lambda }_{\mathrm {fin}} \to \widehat {\Lambda }_{\mathrm {fin}}$
with
The second equalities in this last pair of definitions rely on Theorems 4.13 and 4.20.
The operators
![]() $ \mathfrak {p}(t) $
,
$ \mathfrak {p}(t) $
,
![]() $ \mathfrak {q}(t)$
,
$ \mathfrak {q}(t)$
,
![]() $ \tilde {\mathfrak {p}}(t) $
,
$ \tilde {\mathfrak {p}}(t) $
,
![]() $ \tilde {\mathfrak {q}}(t)$
all make sense as maps
$ \tilde {\mathfrak {q}}(t)$
all make sense as maps
![]() ${\Lambda } \to {\Lambda }$
but not as maps
${\Lambda } \to {\Lambda }$
but not as maps
![]() $\widehat {\Lambda } \to \widehat {\Lambda }$
. For example, the coefficient of
$\widehat {\Lambda } \to \widehat {\Lambda }$
. For example, the coefficient of
![]() $\emptyset $
in the image of
$\emptyset $
in the image of
![]() $(1) + (2) + (3) + \dots \in \widehat {\Lambda } - \widehat {\Lambda }_{\mathrm {fin}}$
under any of these operators would be in
$(1) + (2) + (3) + \dots \in \widehat {\Lambda } - \widehat {\Lambda }_{\mathrm {fin}}$
under any of these operators would be in ![]() rather than
rather than ![]() . These operators send
. These operators send
![]() $\widehat {\Lambda }_{\mathrm {fin}}\to \widehat {\Lambda }_{\mathrm {fin}}$
because they each map
$\widehat {\Lambda }_{\mathrm {fin}}\to \widehat {\Lambda }_{\mathrm {fin}}$
because they each map
![]() $\lambda $
into the
$\lambda $
into the ![]() -span of the finite set of strict partitions
-span of the finite set of strict partitions
![]() $\mu \subseteq \lambda $
.
$\mu \subseteq \lambda $
.
Lemma 4.21. It holds that
![]() $\mathfrak {p}(-t)\tilde {\mathfrak {p}}(t) = \tilde {\mathfrak {p}}(t)\mathfrak {p}(-t) = \mathfrak {q}(-t)\tilde {\mathfrak {q}}(t) = \tilde {\mathfrak {q}}(t)\mathfrak {q}(-t) = 1$
.
$\mathfrak {p}(-t)\tilde {\mathfrak {p}}(t) = \tilde {\mathfrak {p}}(t)\mathfrak {p}(-t) = \mathfrak {q}(-t)\tilde {\mathfrak {q}}(t) = \tilde {\mathfrak {q}}(t)\mathfrak {q}(-t) = 1$
.
Proof. For each integer
![]() $j>0$
, let
$j>0$
, let
![]() $r_j $
,
$r_j $
,
![]() $c_j$
and
$c_j$
and
![]() $b_j$
be the linear maps
$b_j$
be the linear maps
![]() ${\Lambda } \to {\Lambda } $
with
${\Lambda } \to {\Lambda } $
with
 $$\begin{align*}\begin{aligned} r_j(\lambda) &= \sum (-\beta)^{|\mu|-|\lambda|-1} \mu, \\ c_j(\lambda) &= \sum (-\beta)^{|\nu|-|\lambda|-1} \nu, \\ b_j(\lambda) &= \sum (-\beta)^{|\kappa|-|\lambda|-1} \kappa, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} r_j(\lambda) &= \sum (-\beta)^{|\mu|-|\lambda|-1} \mu, \\ c_j(\lambda) &= \sum (-\beta)^{|\nu|-|\lambda|-1} \nu, \\ b_j(\lambda) &= \sum (-\beta)^{|\kappa|-|\lambda|-1} \kappa, \end{aligned} \end{align*}$$
where the sums are respectively over the finite sets of strict partitions
![]() $\mu \subsetneq \lambda $
,
$\mu \subsetneq \lambda $
,
![]() $\nu \subsetneq \lambda $
and
$\nu \subsetneq \lambda $
and
![]() $\kappa \subsetneq \lambda $
such that
$\kappa \subsetneq \lambda $
such that
![]() $\textsf {SD}_{\lambda /\mu }$
is contained in row j,
$\textsf {SD}_{\lambda /\mu }$
is contained in row j,
![]() $\textsf {SD}_{\lambda /\nu }$
is contained in column j, and
$\textsf {SD}_{\lambda /\nu }$
is contained in column j, and
![]() $\textsf {SD}_{\lambda /\kappa }$
is contained in column j but does not contain a box on the main diagonal. Next, fix an integer
$\textsf {SD}_{\lambda /\kappa }$
is contained in column j but does not contain a box on the main diagonal. Next, fix an integer
![]() $n>0$
and define
$n>0$
and define
 $$\begin{align*}\begin{aligned} R_n(t)& := (1+t r_1)(1+tr_2) \cdots (1+tr_n), \\ C_n(t) &:= (1+tc_1)(1+tc_2)\cdots (1+tc_n), \\ B_n(t) &:= (1+t b_1)(1+t b_2)\cdots (1+t b_n), \end{aligned} \quad\text{and}\quad \begin{aligned} \tilde R_n(t)& := \tfrac{1}{1-t r_n} \cdots\tfrac{1}{1-tr_2}\tfrac{1}{1-tr_1}, \\ \tilde C_n(t) &:= \tfrac{1}{1-t c_n} \cdots\tfrac{1}{1-tc_2}\tfrac{1}{1-tc_1} , \\ \tilde B_n(t) &:= \tfrac{1}{1-t b_n} \cdots\tfrac{1}{1-t b_2}\tfrac{1}{1-tb_1}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} R_n(t)& := (1+t r_1)(1+tr_2) \cdots (1+tr_n), \\ C_n(t) &:= (1+tc_1)(1+tc_2)\cdots (1+tc_n), \\ B_n(t) &:= (1+t b_1)(1+t b_2)\cdots (1+t b_n), \end{aligned} \quad\text{and}\quad \begin{aligned} \tilde R_n(t)& := \tfrac{1}{1-t r_n} \cdots\tfrac{1}{1-tr_2}\tfrac{1}{1-tr_1}, \\ \tilde C_n(t) &:= \tfrac{1}{1-t c_n} \cdots\tfrac{1}{1-tc_2}\tfrac{1}{1-tc_1} , \\ \tilde B_n(t) &:= \tfrac{1}{1-t b_n} \cdots\tfrac{1}{1-t b_2}\tfrac{1}{1-tb_1}. \end{aligned} \end{align*}$$
Here, we interpret
![]() $\tfrac {1}{1-t r_j} $
as the geometric series
$\tfrac {1}{1-t r_j} $
as the geometric series
![]() $1 + t r_j + t^2 r_j^2 + \dots $
(and likewise for
$1 + t r_j + t^2 r_j^2 + \dots $
(and likewise for
![]() $\tfrac {1}{1-t c_j} $
and
$\tfrac {1}{1-t c_j} $
and
![]() $\tfrac {1}{1-t b_j} $
); this makes sense as maps
$\tfrac {1}{1-t b_j} $
); this makes sense as maps
![]() ${\Lambda } \to {\Lambda } $
because
${\Lambda } \to {\Lambda } $
because
![]() $r_j$
,
$r_j$
,
![]() $c_j$
and
$c_j$
and
![]() $b_j$
are locally nilpotent (i.e., for each
$b_j$
are locally nilpotent (i.e., for each
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $r_j^m(\lambda ) = 0$
for sufficiently large m).
$r_j^m(\lambda ) = 0$
for sufficiently large m).
Now suppose
![]() $\lambda $
is a strict partition whose shifted diagram fits inside
$\lambda $
is a strict partition whose shifted diagram fits inside
![]() $[n]\times [n]$
. By construction,
$[n]\times [n]$
. By construction,
Here, one should think of
![]() $C_n(t)$
as carving out space from
$C_n(t)$
as carving out space from
![]() $\lambda $
for the unprimed entries in a ShRPP while
$\lambda $
for the unprimed entries in a ShRPP while
![]() $R_n(t)$
carves out space for the primed entries. However,
$R_n(t)$
carves out space for the primed entries. However,
![]() $ \tilde R_n(t) $
carves out space from
$ \tilde R_n(t) $
carves out space from
![]() $\lambda $
for the unprimed row bars in a ShBT while
$\lambda $
for the unprimed row bars in a ShBT while
![]() $ \tilde C_n(t) $
carves out space for the primed column bars. Since
$ \tilde C_n(t) $
carves out space for the primed column bars. Since
![]() $\textsf {SD}_\mu \subseteq [n]\times [n]$
for all
$\textsf {SD}_\mu \subseteq [n]\times [n]$
for all
![]() $\mu \subseteq \lambda $
, it follows that
$\mu \subseteq \lambda $
, it follows that
 $$\begin{align*}\begin{aligned} \tilde{\mathfrak{q}}(-t) \mathfrak{q}(t) \lambda & = \sum_{\mu \subseteq \lambda} g\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu}(t) \tilde{\mathfrak{q}}(-t)\mu =\sum_{\mu \subseteq \lambda} g\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu}(t) \tilde C_n(-t) \tilde R_n(-t)\mu \\ & = \tilde C_n(-t) \tilde R_n(-t) R_n(t) C_n(t) \lambda. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \tilde{\mathfrak{q}}(-t) \mathfrak{q}(t) \lambda & = \sum_{\mu \subseteq \lambda} g\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu}(t) \tilde{\mathfrak{q}}(-t)\mu =\sum_{\mu \subseteq \lambda} g\hspace{-0.1mm}q^{\mathrm{comb}}_{\lambda/\mu}(t) \tilde C_n(-t) \tilde R_n(-t)\mu \\ & = \tilde C_n(-t) \tilde R_n(-t) R_n(t) C_n(t) \lambda. \end{aligned} \end{align*}$$
Since
![]() $ \tilde R_n(-t) R_n(t) = \tilde C_n(-t) C_n(t) = 1$
, we have
$ \tilde R_n(-t) R_n(t) = \tilde C_n(-t) C_n(t) = 1$
, we have
![]() $\tilde {\mathfrak {q}}(-t) \mathfrak {q}(t) \lambda = \lambda $
, and a similar calculation shows
$\tilde {\mathfrak {q}}(-t) \mathfrak {q}(t) \lambda = \lambda $
, and a similar calculation shows
![]() $\mathfrak {q}(t) \tilde {\mathfrak {q}}(-t) \lambda = \lambda $
. Since n can be arbitrary, so that
$\mathfrak {q}(t) \tilde {\mathfrak {q}}(-t) \lambda = \lambda $
. Since n can be arbitrary, so that
![]() $\lambda $
can also be arbitrary, we conclude that
$\lambda $
can also be arbitrary, we conclude that
![]() $\mathfrak {q}(-t)\tilde {\mathfrak {q}}(t) = \tilde {\mathfrak {q}}(t)\mathfrak {q}(-t) = 1$
. The identity
$\mathfrak {q}(-t)\tilde {\mathfrak {q}}(t) = \tilde {\mathfrak {q}}(t)\mathfrak {q}(-t) = 1$
. The identity
![]() $\mathfrak {p}(-t)\tilde {\mathfrak {p}}(t) = \tilde {\mathfrak {p}}(t)\mathfrak {p}(-t) = 1$
follows by a similar argument since
$\mathfrak {p}(-t)\tilde {\mathfrak {p}}(t) = \tilde {\mathfrak {p}}(t)\mathfrak {p}(-t) = 1$
follows by a similar argument since
![]() $ \mathfrak {p}(t) \lambda = R_n(t) B_n(t) \lambda $
and
$ \mathfrak {p}(t) \lambda = R_n(t) B_n(t) \lambda $
and
![]() $ \tilde {\mathfrak {p}}(t) \lambda = \tilde B_n(t) \tilde R_n(t) \lambda $
when
$ \tilde {\mathfrak {p}}(t) \lambda = \tilde B_n(t) \tilde R_n(t) \lambda $
when
![]() $\textsf {SD}_\lambda \subseteq [n]\times [n]$
.
$\textsf {SD}_\lambda \subseteq [n]\times [n]$
.
Fix ![]() with
with
![]() $\mathrm {mindeg}(u)=\mathrm {mindeg}(v)=1$
. Recall
$\mathrm {mindeg}(u)=\mathrm {mindeg}(v)=1$
. Recall
![]() $\overline {x} := \frac {-x}{1+\beta x}$
.
$\overline {x} := \frac {-x}{1+\beta x}$
.
Lemma 4.22. The following identities hold:
Proof. For any strict partitions
![]() $\mu $
and
$\mu $
and
![]() $\nu $
, the Cauchy identity (2.9) implies that
$\nu $
, the Cauchy identity (2.9) implies that
(after setting
![]() $x_1 = u$
,
$x_1 = u$
,
![]() $y_1 = v$
, and all other variables to
$y_1 = v$
, and all other variables to
![]() $0$
). The first identity holds since we have
$0$
). The first identity holds since we have
![]() $\langle \mathcal {Q}(v) \tilde {\mathfrak {p}}(u)\mu , \nu \rangle = \sum _\kappa G\hspace {-0.2mm}Q_{\nu /\hspace {-1mm}/\kappa }(u) j\hspace {-0.1mm}p_{\mu /\kappa }(v)$
. The second identity follows similarly using (2.8).
$\langle \mathcal {Q}(v) \tilde {\mathfrak {p}}(u)\mu , \nu \rangle = \sum _\kappa G\hspace {-0.2mm}Q_{\nu /\hspace {-1mm}/\kappa }(u) j\hspace {-0.1mm}p_{\mu /\kappa }(v)$
. The second identity follows similarly using (2.8).
Corollary 4.23. The following identities hold:
Proof. Consider the first identity in Lemma 4.22. Multiplying both sides on the left and right by
![]() $\mathfrak {p}(-v)$
gives
$\mathfrak {p}(-v)$
gives
![]() $\mathcal {Q}(u)\mathfrak {p}(-v) =\tfrac {1+uv}{1+\overline {u}v} \mathfrak {p}(-v) \mathcal {Q}(u)$
by Lemma 4.21. Thus,
$\mathcal {Q}(u)\mathfrak {p}(-v) =\tfrac {1+uv}{1+\overline {u}v} \mathfrak {p}(-v) \mathcal {Q}(u)$
by Lemma 4.21. Thus,
![]() $ \mathfrak {p}(-v) \mathcal {Q}(u) = \tfrac {1+\overline {u}v} {1+uv} \mathcal {Q}(u)\mathfrak {p}(-v)$
, and this becomes the first desired identity on negating v. The other identity follows similarly.
$ \mathfrak {p}(-v) \mathcal {Q}(u) = \tfrac {1+\overline {u}v} {1+uv} \mathcal {Q}(u)\mathfrak {p}(-v)$
, and this becomes the first desired identity on negating v. The other identity follows similarly.
Putting together all of these identities lets us prove our last main theorem.
Theorem 4.24. If
![]() $\mu $
and
$\mu $
and
![]() $ \lambda $
are strict partitions, then
$ \lambda $
are strict partitions, then
Proof. Fix an integer
![]() $n>0$
. Then one has
$n>0$
. Then one has
![]() $ \langle \mathcal {Q}(x_n)\cdots \mathcal {Q}(x_2)\mathcal {Q}(x_1) \emptyset , \lambda \rangle = G\hspace {-0.2mm}Q_{\lambda }(x_1,x_2,\dots ,x_n) $
and
$ \langle \mathcal {Q}(x_n)\cdots \mathcal {Q}(x_2)\mathcal {Q}(x_1) \emptyset , \lambda \rangle = G\hspace {-0.2mm}Q_{\lambda }(x_1,x_2,\dots ,x_n) $
and
![]() $ \langle \mathfrak {p}(x_1)\mathfrak {p}(x_2)\cdots \mathfrak {p}(x_n) \lambda , \emptyset \rangle = g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda }(x_1,x_2,\dots ,x_n) $
for any strict partition
$ \langle \mathfrak {p}(x_1)\mathfrak {p}(x_2)\cdots \mathfrak {p}(x_n) \lambda , \emptyset \rangle = g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda }(x_1,x_2,\dots ,x_n) $
for any strict partition
![]() $\lambda $
, so by Corollary 4.23,
$\lambda $
, so by Corollary 4.23,
 $$\begin{align*}\begin{aligned} \sum_\lambda G\hspace{-0.2mm}Q_\lambda(x_1,\dots,x_n) g\hspace{-0.1mm}p^{\mathrm{comb}}_\lambda(y_1,\dots,y_n) &= \langle \mathfrak{p}(y_1) \mathfrak{p}(y_2)\cdots \mathfrak{p}(y_n) \mathcal{Q}(x_n)\cdots\mathcal{Q}(x_2)\mathcal{Q}(x_1) \emptyset, \emptyset \rangle \\&= \prod_{1\leq i,j\leq n} \tfrac{1-\overline{x_i}y_j}{1-x_iy_j} \langle \mathcal{Q}(x_n) \cdots \mathcal{Q}(x_1) \mathfrak{p}(y_1)\cdots \mathfrak{p}(y_n) \emptyset, \emptyset \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \sum_\lambda G\hspace{-0.2mm}Q_\lambda(x_1,\dots,x_n) g\hspace{-0.1mm}p^{\mathrm{comb}}_\lambda(y_1,\dots,y_n) &= \langle \mathfrak{p}(y_1) \mathfrak{p}(y_2)\cdots \mathfrak{p}(y_n) \mathcal{Q}(x_n)\cdots\mathcal{Q}(x_2)\mathcal{Q}(x_1) \emptyset, \emptyset \rangle \\&= \prod_{1\leq i,j\leq n} \tfrac{1-\overline{x_i}y_j}{1-x_iy_j} \langle \mathcal{Q}(x_n) \cdots \mathcal{Q}(x_1) \mathfrak{p}(y_1)\cdots \mathfrak{p}(y_n) \emptyset, \emptyset \rangle. \end{aligned} \end{align*}$$
As
![]() $\mathfrak {p}(t) \emptyset = \emptyset $
,
$\mathfrak {p}(t) \emptyset = \emptyset $
,
![]() $\langle \mathcal {Q}(t) \emptyset ,\emptyset \rangle = 1$
, and
$\langle \mathcal {Q}(t) \emptyset ,\emptyset \rangle = 1$
, and
![]() $\langle \mathcal {Q}(t) \mu ,\emptyset \rangle = 0$
for
$\langle \mathcal {Q}(t) \mu ,\emptyset \rangle = 0$
for
![]() $\mu \neq \emptyset $
, we get
$\mu \neq \emptyset $
, we get
 $$\begin{align*}\sum_\lambda G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) g\hspace{-0.1mm}p^{\mathrm{comb}}_\lambda(\mathbf{y}) = \prod_{i,j\geq 1} \tfrac{1-\overline{x_i}y_j}{1-x_iy_j}\end{align*}$$
$$\begin{align*}\sum_\lambda G\hspace{-0.2mm}Q_\lambda(\mathbf{x}) g\hspace{-0.1mm}p^{\mathrm{comb}}_\lambda(\mathbf{y}) = \prod_{i,j\geq 1} \tfrac{1-\overline{x_i}y_j}{1-x_iy_j}\end{align*}$$
by taking
![]() $n\to \infty $
. This is the Cauchy identity (1.1) defining
$n\to \infty $
. This is the Cauchy identity (1.1) defining
![]() $g\hspace {-0.1mm}p_\lambda $
, so
$g\hspace {-0.1mm}p_\lambda $
, so
![]() $g\hspace {-0.1mm}p_\lambda = g\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda $
. In particular, this means that
$g\hspace {-0.1mm}p_\lambda = g\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda $
. In particular, this means that
![]() $g\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda $
is symmetric. It therefore follows from the definition of
$g\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda $
is symmetric. It therefore follows from the definition of
![]() $g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
that
$g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
that
![]() $g\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda (\mathbf {x},\mathbf {y}) = \sum _{\mu }g\hspace {-0.1mm}p^{\mathrm {comb}}_\mu (\mathbf {x}) g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }(\mathbf {y})$
. On comparing this with (2.5), we conclude that
$g\hspace {-0.1mm}p^{\mathrm {comb}}_\lambda (\mathbf {x},\mathbf {y}) = \sum _{\mu }g\hspace {-0.1mm}p^{\mathrm {comb}}_\mu (\mathbf {x}) g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }(\mathbf {y})$
. On comparing this with (2.5), we conclude that
![]() $g\hspace {-0.1mm}p_{\lambda /\mu } = g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
for all
$g\hspace {-0.1mm}p_{\lambda /\mu } = g\hspace {-0.1mm}p^{\mathrm {comb}}_{\lambda /\mu }$
for all
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
. A similar argument using
$\mu $
. A similar argument using
![]() $\mathfrak {q}(t)$
and
$\mathfrak {q}(t)$
and
![]() $\mathcal {P}(t)$
shows that
$\mathcal {P}(t)$
shows that
![]() $g\hspace {-0.1mm}q_{\lambda /\mu } = g\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
.
$g\hspace {-0.1mm}q_{\lambda /\mu } = g\hspace {-0.1mm}q^{\mathrm {comb}}_{\lambda /\mu }$
.
Competing interests
The authors have no competing interest to declare.
Financial support
The first author was partially supported by Simons Foundation grant 634530. The second author was partially supported by Hong Kong RGC grant GRF 16306120.