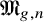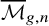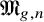1 Introduction
Let
![]() $\overline {\mathcal {M}}_{g,n}$
be the moduli space of stable curves. It parameterises tuples
$\overline {\mathcal {M}}_{g,n}$
be the moduli space of stable curves. It parameterises tuples
![]() $(C,p_1, \ldots , p_n)$
of a nodal curve C of arithmetic genus g with n distinct smooth marked points such that C has only finitely many automorphisms fixing the points
$(C,p_1, \ldots , p_n)$
of a nodal curve C of arithmetic genus g with n distinct smooth marked points such that C has only finitely many automorphisms fixing the points
![]() $p_i$
. After Mumford’s seminal paper [Reference MumfordMum83], there has been a substantial study of the structure of the tautological rings
$p_i$
. After Mumford’s seminal paper [Reference MumfordMum83], there has been a substantial study of the structure of the tautological rings
The tautological rings form a system of subrings of
![]() $\mathrm {CH}^{*}(\overline {\mathcal {M}}_{g,n})_{\mathbb {Q}}$
with explicit generators defined using the universal curve and the boundary gluing maps of the spaces
$\mathrm {CH}^{*}(\overline {\mathcal {M}}_{g,n})_{\mathbb {Q}}$
with explicit generators defined using the universal curve and the boundary gluing maps of the spaces
![]() $\overline {\mathcal {M}}_{g,n}$
; see [Reference Graber and PandharipandeGP03].
$\overline {\mathcal {M}}_{g,n}$
; see [Reference Graber and PandharipandeGP03].
A natural extension of
![]() $\overline {\mathcal {M}}_{g,n}$
is the moduli stack
$\overline {\mathcal {M}}_{g,n}$
is the moduli stack
![]() $\mathfrak {M}_{g,n}$
of marked prestable curves, in which we drop the condition of having only finitely many automorphisms. It is a smooth algebraic stack, locally of finite type over the base field k and containing
$\mathfrak {M}_{g,n}$
of marked prestable curves, in which we drop the condition of having only finitely many automorphisms. It is a smooth algebraic stack, locally of finite type over the base field k and containing
![]() $\overline {\mathcal {M}}_{g,n}$
as an open substack. However, by allowing infinite automorphism groups, the stacks of prestable curves are no longer Deligne-Mumford stacks and not of finite type.Footnote
1
$\overline {\mathcal {M}}_{g,n}$
as an open substack. However, by allowing infinite automorphism groups, the stacks of prestable curves are no longer Deligne-Mumford stacks and not of finite type.Footnote
1
A recent application of Chow groups of such non-finite type algebraic stacks appeared in the paper [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20], which studied cycle classes and tautological rings for the universal Picard stack
![]() $\mathfrak {Pic}_{g}$
over the stack
$\mathfrak {Pic}_{g}$
over the stack
![]() $\mathfrak {M}_{g}$
. The stack
$\mathfrak {M}_{g}$
. The stack
![]() $\mathfrak {Pic}_{g}$
parameterises pairs
$\mathfrak {Pic}_{g}$
parameterises pairs
![]() $(C,\mathcal {L})$
of a prestable curve C and a line bundle
$(C,\mathcal {L})$
of a prestable curve C and a line bundle
![]() $\mathcal {L}$
on C. In [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20], results from [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ20] are used to prove a formula for the fundamental class of the closure of the zero section
$\mathcal {L}$
on C. In [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20], results from [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ20] are used to prove a formula for the fundamental class of the closure of the zero section
![]() $\{(C, \mathcal {O}_C)\} \subseteq \mathfrak {Pic}_{g}$
. By pulling back this equality under natural morphisms
$\{(C, \mathcal {O}_C)\} \subseteq \mathfrak {Pic}_{g}$
. By pulling back this equality under natural morphisms
![]() $\overline {\mathcal {M}}_{g,n} \to \mathfrak {Pic}_{g}$
, new results about the classical double ramification cycles on the moduli of stable curves are established.
$\overline {\mathcal {M}}_{g,n} \to \mathfrak {Pic}_{g}$
, new results about the classical double ramification cycles on the moduli of stable curves are established.
In the paper [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20], the intersection theory of
![]() $\mathfrak {Pic}_{g}$
is studied using a definition of operational Chow groups modelled on [Reference FultonFul98, Chapter 17]. In our paper, we follow the approach [Reference KreschKre99] by Kresch, who developed a cycle theory for algebraic stacks of finite type over a field k. This theory has many structural advantages over the operational theory of [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20], such as projective pushforwards and an excision sequence, and for a smooth stack always admits a natural map to this operational theory.Footnote
2
$\mathfrak {Pic}_{g}$
is studied using a definition of operational Chow groups modelled on [Reference FultonFul98, Chapter 17]. In our paper, we follow the approach [Reference KreschKre99] by Kresch, who developed a cycle theory for algebraic stacks of finite type over a field k. This theory has many structural advantages over the operational theory of [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20], such as projective pushforwards and an excision sequence, and for a smooth stack always admits a natural map to this operational theory.Footnote
2
We extend Kresch’s theory from the case of finite-type stacks to the case of algebraic stacks
![]() $\mathfrak {X}$
locally of finite type over k (such as
$\mathfrak {X}$
locally of finite type over k (such as
![]() $\mathfrak {M}_{g,n}$
) by defining their Chow groupsFootnote
3
as the limit
$\mathfrak {M}_{g,n}$
) by defining their Chow groupsFootnote
3
as the limit
for
![]() $(\mathcal U_i)_{i \in I}$
a directed system of finite-type open substacks covering
$(\mathcal U_i)_{i \in I}$
a directed system of finite-type open substacks covering
![]() $\mathfrak {X}$
. Using this definition, we define the tautological ring
$\mathfrak {X}$
. Using this definition, we define the tautological ring
![]() $\mathrm {R}^*(\mathfrak {M}_{g,n}) \subseteq \mathrm {CH}^*(\mathfrak {M}_{g,n})$
, extending the definition [Reference Graber and PandharipandeGP03] for the moduli spaces of stable curves.Footnote
4
$\mathrm {R}^*(\mathfrak {M}_{g,n}) \subseteq \mathrm {CH}^*(\mathfrak {M}_{g,n})$
, extending the definition [Reference Graber and PandharipandeGP03] for the moduli spaces of stable curves.Footnote
4
Proper pushforwards of Chow groups of algebraic stacks
When extending the definition of the tautological ring to the stacks of prestable curves, we immediately encounter a problem: for the spaces
![]() $\overline {\mathcal {M}}_{g,n}$
of stable curves, these rings can be defined as the smallest system of subrings of
$\overline {\mathcal {M}}_{g,n}$
of stable curves, these rings can be defined as the smallest system of subrings of
![]() $\mathrm {CH}^*(\overline {\mathcal {M}}_{g,n})$
closed under pushforwards by gluing morphisms and the morphisms
$\mathrm {CH}^*(\overline {\mathcal {M}}_{g,n})$
closed under pushforwards by gluing morphisms and the morphisms
![]() $\overline {\mathcal {C}}_{g,n} = \overline {\mathcal {M}}_{g,n+1} \to \overline {\mathcal {M}}_{g,n}$
giving the universal curve over
$\overline {\mathcal {C}}_{g,n} = \overline {\mathcal {M}}_{g,n+1} \to \overline {\mathcal {M}}_{g,n}$
giving the universal curve over
![]() $\overline {\mathcal {M}}_{g,n}$
. However, for the stacks
$\overline {\mathcal {M}}_{g,n}$
. However, for the stacks
![]() $\mathfrak {M}_{g,n}$
of prestable curves, the analogous universal curve morphisms are in general proper, but not projective (see [Reference FulghesuFul10b, Example 2.3]). Thus Kresch’s Chow theory, which a priori only has projective pushforwards, cannot be applied immediately. Historically, this has been a major obstruction in the study of the Chow groups
$\mathfrak {M}_{g,n}$
of prestable curves, the analogous universal curve morphisms are in general proper, but not projective (see [Reference FulghesuFul10b, Example 2.3]). Thus Kresch’s Chow theory, which a priori only has projective pushforwards, cannot be applied immediately. Historically, this has been a major obstruction in the study of the Chow groups
![]() $\mathrm {CH}^*(\mathfrak {M}_{g,n})$
and made it necessary to give many ad hoc constructions of classes that are traditionally defined by proper pushforwards (see [Reference FulghesuFul10c, Reference FulghesuFul10a]).
$\mathrm {CH}^*(\mathfrak {M}_{g,n})$
and made it necessary to give many ad hoc constructions of classes that are traditionally defined by proper pushforwards (see [Reference FulghesuFul10c, Reference FulghesuFul10a]).
To overcome this obstacle, jointly with Skowera, we define proper pushforwards for cycle groups of algebraic stacks. The corresponding results are included as Appendix B to our paper. We state here the main properties of this construction.
Theorem 1.1 (see Theorem B.17 and Proposition B.18)
Let Y be a stack stratified by global quotient stacks, and let
![]() $f : X \to Y$
be a proper, representable morphism. Then there is a proper pushforward
$f : X \to Y$
be a proper, representable morphism. Then there is a proper pushforward
![]() $f_* : \mathrm {CH}_d(X,\mathbb {Z}) \to \mathrm {CH}_d(Y,\mathbb {Z})$
for all d that is functorial (with respect to compositions) and compatible with flat pullbacks and refined Gysin pullbacks.
$f_* : \mathrm {CH}_d(X,\mathbb {Z}) \to \mathrm {CH}_d(Y,\mathbb {Z})$
for all d that is functorial (with respect to compositions) and compatible with flat pullbacks and refined Gysin pullbacks.
If, instead, f is proper and of relative Deligne-Mumford type, then there is a proper pushforward
![]() $f_* : \mathrm {CH}_d(X, \mathbb {Q}) \to \mathrm {CH}_d(Y, \mathbb {Q})$
for all d, with the properties above.
$f_* : \mathrm {CH}_d(X, \mathbb {Q}) \to \mathrm {CH}_d(Y, \mathbb {Q})$
for all d, with the properties above.
The universal curve over the stack of prestable curves
A second problem we encounter when generalizing the definition of the tautological ring of
![]() $\overline {\mathcal {M}}_{g,n}$
to
$\overline {\mathcal {M}}_{g,n}$
to
![]() $\mathfrak {M}_{g,n}$
is that the universal curve
$\mathfrak {M}_{g,n}$
is that the universal curve
![]() $\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
is not given by the forgetful map
$\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
is not given by the forgetful map
![]() $\mathfrak {M}_{g,n+1} \to \mathfrak {M}_{g,n}$
. In particular, since the forgetful maps are in general not proper, we cannot define
$\mathfrak {M}_{g,n+1} \to \mathfrak {M}_{g,n}$
. In particular, since the forgetful maps are in general not proper, we cannot define
![]() $(\mathrm {R}^*(\mathfrak {M}_{g,n}))_{g,n}$
as the smallest system of subrings of
$(\mathrm {R}^*(\mathfrak {M}_{g,n}))_{g,n}$
as the smallest system of subrings of
![]() $(\mathrm {CH}^*(\mathfrak {M}_{g,n}))_{g,n}$
closed under gluing and forgetful pushforwards.
$(\mathrm {CH}^*(\mathfrak {M}_{g,n}))_{g,n}$
closed under gluing and forgetful pushforwards.
To overcome this issue (and give a modular interpretation of
![]() $\mathfrak {C}_{g,n}$
as a stack of
$\mathfrak {C}_{g,n}$
as a stack of
![]() $(n+1)$
-pointed curves), we use the notion of prestable curves with values in a semigroup
$(n+1)$
-pointed curves), we use the notion of prestable curves with values in a semigroup
![]() $\mathcal {A}$
from [Reference Behrend and ManinBM96, Reference CostelloCos06]. Given a suitable (commutative) semigroupFootnote
5
$\mathcal {A}$
from [Reference Behrend and ManinBM96, Reference CostelloCos06]. Given a suitable (commutative) semigroupFootnote
5
![]() $\mathcal {A}$
and an element
$\mathcal {A}$
and an element
![]() $a \in \mathcal {A}$
, these references define a stack
$a \in \mathcal {A}$
, these references define a stack
![]() $\mathfrak {M}_{g,n,a}$
parameterizing tuples
$\mathfrak {M}_{g,n,a}$
parameterizing tuples
![]() $(C,p_1, \ldots , p_n, (a_{C_v})_v)$
of a prestable curve
$(C,p_1, \ldots , p_n, (a_{C_v})_v)$
of a prestable curve
![]() $(C,p_1, \ldots , p_n)$
together with a value
$(C,p_1, \ldots , p_n)$
together with a value
![]() $a_{C_v} \in \mathcal {A}$
for each component
$a_{C_v} \in \mathcal {A}$
for each component
![]() $C_v$
of C such that all
$C_v$
of C such that all
![]() $a_{C_v}$
sum up to a in
$a_{C_v}$
sum up to a in
![]() $\mathcal {A}$
. Moreover, in contrast to the stack
$\mathcal {A}$
. Moreover, in contrast to the stack
![]() $\mathfrak {M}_{g,n}$
, the definition of
$\mathfrak {M}_{g,n}$
, the definition of
![]() $\mathfrak {M}_{g,n,a}$
includes a stability condition: any component
$\mathfrak {M}_{g,n,a}$
includes a stability condition: any component
![]() $C_v$
such that
$C_v$
such that
![]() is the neutral element of
is the neutral element of
![]() $\mathcal {A}$
must actually be stable: that is, have a finite group of automorphisms fixing all markings and nodes on
$\mathcal {A}$
must actually be stable: that is, have a finite group of automorphisms fixing all markings and nodes on
![]() $C_v$
. The advantage of this stability condition is that the natural forgetful map
$C_v$
. The advantage of this stability condition is that the natural forgetful map
![]() $\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
, which forgets the last marking and contracts the component containing it if it becomes unstable, does define the universal curve over
$\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
, which forgets the last marking and contracts the component containing it if it becomes unstable, does define the universal curve over
![]() $\mathfrak {M}_{g,n,a}$
.
$\mathfrak {M}_{g,n,a}$
.
Applying this machinery to a particularly simple semigroup, we obtain the desired modular interpretation of
![]() $\mathfrak {C}_{g,n}$
. For this, consider the semigroup
$\mathfrak {C}_{g,n}$
. For this, consider the semigroup
Then we show the following.
Proposition 1.2 (see Proposition 2.7, Corollary 2.8)
Let
![]() $g,n \geq 0$
, and consider the semigroup
$g,n \geq 0$
, and consider the semigroup
above. Then the stack
![]() $\mathfrak {M}_{g,n}$
is naturally contained inside
$\mathfrak {M}_{g,n}$
is naturally contained inside
as the open substack of
![]() $(C,p_1, \ldots , p_n, (a_{C_v})_v)$
such that
$(C,p_1, \ldots , p_n, (a_{C_v})_v)$
such that
for all v. Thus the universal curve
![]() $\mathfrak {C}_{g,n}$
is naturally contained as an open substack of
$\mathfrak {C}_{g,n}$
is naturally contained as an open substack of
sitting in the Cartesian diagram

In particular, this proposition indeed gives an interpretation of
![]() $\mathfrak {C}_{g,n}$
as a stack of
$\mathfrak {C}_{g,n}$
as a stack of
![]() $(n+1)$
-pointed prestable curves together with some additional structure (see the paragraph below Corollary 2.8 for more details).
$(n+1)$
-pointed prestable curves together with some additional structure (see the paragraph below Corollary 2.8 for more details).
Tautological rings of stacks of prestable curves
Having solved both the issues with proper pushforwards and the modular interpretation of the universal curve, we are now ready to define the tautological rings. Since the discussion in the last section shows that the spaces
![]() $\mathfrak {M}_{g,n,a}$
appear naturally, we will in fact define the tautological rings for these spaces and obtain the rings for
$\mathfrak {M}_{g,n,a}$
appear naturally, we will in fact define the tautological rings for these spaces and obtain the rings for
![]() $\mathfrak {M}_{g,n}$
by restriction. To write down the definition, we note that in addition to the forgetful maps
$\mathfrak {M}_{g,n}$
by restriction. To write down the definition, we note that in addition to the forgetful maps
mentioned above, there also exist gluing maps
for every prestable graph
![]() $\Gamma $
together with an
$\Gamma $
together with an
![]() $\mathcal {A}$
-valuation
$\mathcal {A}$
-valuation
![]() $a: V(\Gamma ) \to \mathcal {A}$
satisfying
$a: V(\Gamma ) \to \mathcal {A}$
satisfying
![]() $\sum _{v \in V(\Gamma )} a(v) = a$
. Here
$\sum _{v \in V(\Gamma )} a(v) = a$
. Here
![]() $V(\Gamma )$
is the set of vertices of the graph
$V(\Gamma )$
is the set of vertices of the graph
![]() $\Gamma $
.
$\Gamma $
.
Definition 1.3. The tautological rings
![]() $(\mathrm {R}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
are defined as the smallest system of
$(\mathrm {R}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
are defined as the smallest system of
![]() $\mathbb {Q}$
-subalgebras with unit of the Chow rings
$\mathbb {Q}$
-subalgebras with unit of the Chow rings
![]() $(\mathrm {CH}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
closed under taking pushforwards by the natural forgetful and gluing maps in equations (1) and (2).
$(\mathrm {CH}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
closed under taking pushforwards by the natural forgetful and gluing maps in equations (1) and (2).
The tautological ring
![]() $\mathrm {R}^*(\mathfrak {M}_{g,n}) \subseteq \mathrm {CH}^*(\mathfrak {M}_{g,n})$
is defined as the image of the restriction of
$\mathrm {R}^*(\mathfrak {M}_{g,n}) \subseteq \mathrm {CH}^*(\mathfrak {M}_{g,n})$
is defined as the image of the restriction of
![]() to the open substack
to the open substack
![]() from Proposition 1.2.
from Proposition 1.2.
Just as for the moduli spaces of stable curves, we define
![]() $\psi $
and
$\psi $
and
![]() $\kappa $
-classes: given
$\kappa $
-classes: given
![]() $1 \leq i \leq n$
, we set
$1 \leq i \leq n$
, we set
where
![]() $\sigma _i : \mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n+1,a}$
is the ith universal section and
$\sigma _i : \mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n+1,a}$
is the ith universal section and
![]() $\omega _{\pi }$
is the relative dualizing sheaf of
$\omega _{\pi }$
is the relative dualizing sheaf of
![]() $\pi $
. Similarly, given
$\pi $
. Similarly, given
![]() $m \geq 0$
, we set
$m \geq 0$
, we set
It is easy to see that both types of classes are in fact tautological. Given any
![]() $\mathcal {A}$
-valued prestable graph
$\mathcal {A}$
-valued prestable graph
![]() $\Gamma $
, consider the products
$\Gamma $
, consider the products
 $$ \begin{align} \alpha = \prod_{v\in V} \left( \prod_{i \in H(v)} \psi_{v,i}^{a_i} \prod_{a=1}^{m_v} \kappa_{v,a}^{b_{v,a}} \right)\in \mathrm{CH}^*(\mathfrak{M}_{\Gamma})\end{align} $$
$$ \begin{align} \alpha = \prod_{v\in V} \left( \prod_{i \in H(v)} \psi_{v,i}^{a_i} \prod_{a=1}^{m_v} \kappa_{v,a}^{b_{v,a}} \right)\in \mathrm{CH}^*(\mathfrak{M}_{\Gamma})\end{align} $$
of
![]() $\psi $
and
$\psi $
and
![]() $\kappa $
-classes on the space
$\kappa $
-classes on the space
![]() $\mathfrak {M}_{\Gamma }$
above. Then we define the decorated stratum class
$\mathfrak {M}_{\Gamma }$
above. Then we define the decorated stratum class
![]() $[\Gamma ,\alpha ]$
as the pushforward
$[\Gamma ,\alpha ]$
as the pushforward
The following result (generalizing [Reference Graber and PandharipandeGP03, Proposition 11]) shows that these classes additively generate the tautological rings.
Theorem 1.4. The tautological ring
![]() $\mathrm {R}^*(\mathfrak {M}_{g,n,a})$
is generated as a
$\mathrm {R}^*(\mathfrak {M}_{g,n,a})$
is generated as a
![]() $\mathbb {Q}$
-vector space by the decorated strata classes
$\mathbb {Q}$
-vector space by the decorated strata classes
![]() $[\Gamma , \alpha ]$
. In addition to being closed under pushforwards by gluing and forgetful maps, the tautological rings are likewise closed under pullbacks by these maps, with explicit formulas describing all these operations on the generators
$[\Gamma , \alpha ]$
. In addition to being closed under pushforwards by gluing and forgetful maps, the tautological rings are likewise closed under pullbacks by these maps, with explicit formulas describing all these operations on the generators
![]() $[\Gamma ,\alpha ]$
.Footnote
6
$[\Gamma ,\alpha ]$
.Footnote
6
This result gives an effective method to perform computations in the Chow rings of the stacks
![]() $\mathfrak {M}_{g,n,a}$
. Moreover, it shows that while both the Chow and the tautological rings of these stacks are in general infinite-dimensional, the individual graded pieces of
$\mathfrak {M}_{g,n,a}$
. Moreover, it shows that while both the Chow and the tautological rings of these stacks are in general infinite-dimensional, the individual graded pieces of
![]() $\mathrm {R}^*(\mathfrak {M}_{g,n,a})$
always have a finite set of generators.
$\mathrm {R}^*(\mathfrak {M}_{g,n,a})$
always have a finite set of generators.
Relations to other work
In this section, we explain how our results relate to previous results on the intersection theory of the stacks
![]() $\mathfrak {M}_{g,n}$
.
$\mathfrak {M}_{g,n}$
.
As a first example, in [Reference GathmannGat03], Gathmann used the pullback formula of
![]() $\psi $
-classes along the stabilization morphism
$\psi $
-classes along the stabilization morphism
![]() $\mathrm {st}\colon \mathfrak {M}_{g,1}\to \overline {\mathcal {M}}_{g,1}$
to prove certain properties of the Gromov-Witten potential. In Section 3.2, we compute arbitrary pullbacks of tautological classes under the stabilization map, in particular recovering Gathmann’s result.
$\mathrm {st}\colon \mathfrak {M}_{g,1}\to \overline {\mathcal {M}}_{g,1}$
to prove certain properties of the Gromov-Witten potential. In Section 3.2, we compute arbitrary pullbacks of tautological classes under the stabilization map, in particular recovering Gathmann’s result.
In [Reference OesinghausOes19], Oesinghaus computed the Chow rings of the open locus
![]() $\mathcal {T} \subset \mathfrak {M}_{0,3}$
of curves with dual graph of the shape
$\mathcal {T} \subset \mathfrak {M}_{0,3}$
of curves with dual graph of the shape

This stack has a natural interpretation as the stack of expanded pairs appearing in [Reference Abramovich, Cadman, Fantechi and WiseACFW13]. Oesinghaus showed that the Chow ring of
![]() $\mathcal {T}$
is given by the known algebra of quasi-symmetric functions
$\mathcal {T}$
is given by the known algebra of quasi-symmetric functions
![]() $\mathrm {QSym}$
(see [Reference Luoto, Mykytiuk and van WilligenburgLMvW13] for an overview). The ring
$\mathrm {QSym}$
(see [Reference Luoto, Mykytiuk and van WilligenburgLMvW13] for an overview). The ring
![]() $\mathrm {QSym}$
has a natural basis
$\mathrm {QSym}$
has a natural basis
![]() $M_J$
(as a
$M_J$
(as a
![]() $\mathbb {Q}$
-vector space) indexed by positive integer vectors
$\mathbb {Q}$
-vector space) indexed by positive integer vectors
![]() $J = (j_1, \ldots , j_k) \in \mathbb {Z}_{\geq 1}^{k}$
of some length
$J = (j_1, \ldots , j_k) \in \mathbb {Z}_{\geq 1}^{k}$
of some length
![]() $k \geq 0$
, and the product
$k \geq 0$
, and the product
![]() $M_J \cdot M_{J'}$
can be defined in terms of a certain shuffle rule on the vectors
$M_J \cdot M_{J'}$
can be defined in terms of a certain shuffle rule on the vectors
![]() $J, J'$
(see [Reference OesinghausOes19, Proposition 2]).
$J, J'$
(see [Reference OesinghausOes19, Proposition 2]).
Oesinghaus’ proof worked by writing down an open exhaustion of
![]() $\mathcal {T}$
by quotient stacks, allowing to write the Chow ring as a certain projective limit of polynomial rings that is known to produce the algebra
$\mathcal {T}$
by quotient stacks, allowing to write the Chow ring as a certain projective limit of polynomial rings that is known to produce the algebra
![]() $\mathrm {QSym}$
. However, due to the nature of this proof, a geometric interpretation for the generators
$\mathrm {QSym}$
. However, due to the nature of this proof, a geometric interpretation for the generators
![]() $M_J$
was not immediately clear (see [Reference OesinghausOes19, Remark 7]). Using the techniques of our paper, we can now answer this question, showing that the generators
$M_J$
was not immediately clear (see [Reference OesinghausOes19, Remark 7]). Using the techniques of our paper, we can now answer this question, showing that the generators
![]() $M_J$
have a concrete interpretation as tautological classes.
$M_J$
have a concrete interpretation as tautological classes.
Proposition 1.5 (see Example 4.3)
For
![]() $J = (j_1, \ldots , j_k) \in \mathbb {Z}_{\geq 1}^{k}$
, the generator
$J = (j_1, \ldots , j_k) \in \mathbb {Z}_{\geq 1}^{k}$
, the generator
![]() $M_J \in \mathrm {QSym} \cong \mathrm {CH}^*(\mathcal {T})$
is given by the restriction of the tautological class
$M_J \in \mathrm {QSym} \cong \mathrm {CH}^*(\mathcal {T})$
is given by the restriction of the tautological class

on
![]() $\mathfrak {M}_{0,3}$
.
$\mathfrak {M}_{0,3}$
.
Furthermore, it is straightforward to see that the shuffle rule describing products
![]() $M_J \cdot M_{J'}$
is an immediate consequence of the product formula for the tautological classes in equation (4). Oesinghaus also computes the Chow rings of the loci
$M_J \cdot M_{J'}$
is an immediate consequence of the product formula for the tautological classes in equation (4). Oesinghaus also computes the Chow rings of the loci
![]() $\mathfrak {M}_{0,2}^{\mathrm {ss}}$
and
$\mathfrak {M}_{0,2}^{\mathrm {ss}}$
and
![]() $\mathfrak {M}_{0,3}^{\mathrm {ss}}$
of semistable curves in
$\mathfrak {M}_{0,3}^{\mathrm {ss}}$
of semistable curves in
![]() $\mathfrak {M}_{0,2}$
and
$\mathfrak {M}_{0,2}$
and
![]() $\mathfrak {M}_{0,3}$
, giving a description in terms of tensor products involving the rings
$\mathfrak {M}_{0,3}$
, giving a description in terms of tensor products involving the rings
![]() $\mathrm {QSym}$
. Again, we give a description in terms of tautological classes in Example 4.3.
$\mathrm {QSym}$
. Again, we give a description in terms of tautological classes in Example 4.3.
Tautological relations in genus zero
The present paper lays down the foundations of the theory of the Chow rings
![]() $\mathrm {CH}^*(\mathfrak {M}_{g,n})$
. In the second part [Reference Bae and SchmittBS21], we use results of this paper to fully determine the Chow rings of
$\mathrm {CH}^*(\mathfrak {M}_{g,n})$
. In the second part [Reference Bae and SchmittBS21], we use results of this paper to fully determine the Chow rings of
![]() $\mathfrak {M}_{0,n}$
for all n: we prove that all classes are tautological, and we compute all relations among generators of the tautological ring.
$\mathfrak {M}_{0,n}$
for all n: we prove that all classes are tautological, and we compute all relations among generators of the tautological ring.
Structure of the paper
In Section 2, we establish basic properties of the stacks
![]() $\mathfrak {M}_{g,n}$
. We discuss boundary gluing maps in Section 2.1 and introduce the stacks of prestable curves with values in a semigroup in Section 2.2. In Section 3, we establish basic properties of the Chow group of
$\mathfrak {M}_{g,n}$
. We discuss boundary gluing maps in Section 2.1 and introduce the stacks of prestable curves with values in a semigroup in Section 2.2. In Section 3, we establish basic properties of the Chow group of
![]() $\mathfrak {M}_{g,n}$
. In Section 3.1, we define Chow groups and tautological rings of such stacks. In Section 3.2, we compute formulas for intersection products and pullbacks and pushforwards of tautological classes under natural maps. In Section 4, we compare our result with previous works by Gathmann [Reference GathmannGat03], Pixton [Reference PixtonPix18] and Oesinghaus [Reference OesinghausOes19].
$\mathfrak {M}_{g,n}$
. In Section 3.1, we define Chow groups and tautological rings of such stacks. In Section 3.2, we compute formulas for intersection products and pullbacks and pushforwards of tautological classes under natural maps. In Section 4, we compare our result with previous works by Gathmann [Reference GathmannGat03], Pixton [Reference PixtonPix18] and Oesinghaus [Reference OesinghausOes19].
In Appendix A, we give some general treatment of Chow groups of locally finite type algebraic stacks. We give a definition of such Chow groups based on [Reference KreschKre99] and show various basic properties. In Appendix B (jointly with J. Skowera), we construct proper pushforwards of cycles, show basic compatibility properties of these pushforwards and explain how they extend to the setting of algebraic stacks locally of finite type. Finally, in Appendix C, we give a definition and establish the basic properties of operational Chow groups on locally finite type stacks, a technical tool needed for some of the computations in Section 3.2.
2 The stack
 $\mathfrak {M}_{g,n}$
of prestable curves
$\mathfrak {M}_{g,n}$
of prestable curves
Throughout the paper, we work over an arbitrary base field k. Let
![]() $\mathfrak {M}_{g,n}$
be the moduli stack of prestable curves of genus g with n marked points. An object of
$\mathfrak {M}_{g,n}$
be the moduli stack of prestable curves of genus g with n marked points. An object of
![]() $\mathfrak {M}_{g,n}$
over a scheme S is a tuple
$\mathfrak {M}_{g,n}$
over a scheme S is a tuple
where C is an algebraic space and the map
![]() $\pi $
is a flat, proper morphism of finite presentation and relative dimension
$\pi $
is a flat, proper morphism of finite presentation and relative dimension
![]() $1$
. The geometric fibres of
$1$
. The geometric fibres of
![]() $\pi $
are connected, reduced curves of arithmetic genus g with at worst nodal singularities. The morphisms
$\pi $
are connected, reduced curves of arithmetic genus g with at worst nodal singularities. The morphisms
![]() $p_1, \ldots , p_n$
are disjoint sections of
$p_1, \ldots , p_n$
are disjoint sections of
![]() $\pi $
with image in the smooth locus of
$\pi $
with image in the smooth locus of
![]() $\pi $
; see [Sta20, 0E6S].
$\pi $
; see [Sta20, 0E6S].
This stack is quasi-separated, smooth and locally of finite type over k ([Reference Alper and KreschAK16]) and of dimension
![]() $3g-3+n$
([Reference BehrendBeh97]). For
$3g-3+n$
([Reference BehrendBeh97]). For
![]() $2g-2+n>0$
, there is a natural stabilization morphism
$2g-2+n>0$
, there is a natural stabilization morphism
that contracts unstable rational components. This morphism is flat by [Reference BehrendBeh97, Proposition 3].
2.1 Boundary gluing maps
A prestable graph
![]() $\Gamma $
of genus g with
$\Gamma $
of genus g with
![]() $n $
markings consists of the data
$n $
markings consists of the data
satisfying the properties:
-
(i) V is a vertex set with a genus function
 $g\colon V\to \mathbb {Z}_{\geq 0}$
,
$g\colon V\to \mathbb {Z}_{\geq 0}$
, -
(ii) H is a half-edge set equipped with a vertex assignment
 $v:H \to V$
and an involution
$v:H \to V$
and an involution
 $\iota $
,
$\iota $
, -
(iii) E, the edge set, is defined by the 2-cycles of
 $\iota $
in H (self-edges at vertices are permitted),
$\iota $
in H (self-edges at vertices are permitted), -
(iv)
 $L \subseteq H$
, the set of legs, is defined by the fixed points of
$L \subseteq H$
, the set of legs, is defined by the fixed points of
 $\iota $
and corresponds to n markings via the bijection
$\iota $
and corresponds to n markings via the bijection
 $\ell : L \to \{1, \ldots , n\}$
,
$\ell : L \to \{1, \ldots , n\}$
, -
(v) the pair
 $(V,E)$
defines a connected graph satisfying the genus condition where
$(V,E)$
defines a connected graph satisfying the genus condition where $$ \begin{align*}\sum_{v \in V} g(v) + h^1(\Gamma) = g,\end{align*} $$
$$ \begin{align*}\sum_{v \in V} g(v) + h^1(\Gamma) = g,\end{align*} $$
 $h^1(\Gamma ) = |E| - |V| + 1$
is the first Betti number of the graph
$h^1(\Gamma ) = |E| - |V| + 1$
is the first Betti number of the graph
 $\Gamma $
.
$\Gamma $
.
A prestable graph
![]() $\Gamma $
is called stable if the following additional condition is satisfied:
$\Gamma $
is called stable if the following additional condition is satisfied:
-
(vi) for each vertex
 $w\in V$
, we have where
$w\in V$
, we have where $$\begin{align*}2g(w)-2+n(w)>0,\end{align*}$$
$$\begin{align*}2g(w)-2+n(w)>0,\end{align*}$$
 $n(w) = |v^{-1}(w)|$
is the valence of w in
$n(w) = |v^{-1}(w)|$
is the valence of w in
 $\Gamma $
: that is, the number of half-edges incident to w.
$\Gamma $
: that is, the number of half-edges incident to w.
Given a second graph
![]() $\Gamma ' = (V',H', \ell ',g',v',\iota ')$
, an isomorphism
$\Gamma ' = (V',H', \ell ',g',v',\iota ')$
, an isomorphism
![]() $\varphi : \Gamma \to \Gamma '$
is the data of bijective maps
$\varphi : \Gamma \to \Gamma '$
is the data of bijective maps
that are compatible with the remaining data of the prestable graphs, in the sense that
For every vertex
![]() $v \in V(\Gamma )$
, let
$v \in V(\Gamma )$
, let
![]() $H(v)$
be the set of half-edges at v, with cardinality
$H(v)$
be the set of half-edges at v, with cardinality
![]() $n(v)$
. Then there exists a natural gluing morphism
$n(v)$
. Then there exists a natural gluing morphism
which assigns to a collection
![]() $((C_v, (p_h)_{h \in H(v)})$
the curve
$((C_v, (p_h)_{h \in H(v)})$
the curve
![]() $(C,p_1, \ldots , p_n)$
obtained by identifying the markings
$(C,p_1, \ldots , p_n)$
obtained by identifying the markings
![]() $p_h, p_{h'}$
for each pair
$p_h, p_{h'}$
for each pair
![]() $(h,h')$
forming an edge of
$(h,h')$
forming an edge of
![]() $\Gamma $
.Footnote
7
Restricting to the preimage of the open substack
$\Gamma $
.Footnote
7
Restricting to the preimage of the open substack
![]() $\overline {\mathcal {M}}_{g,n} \subset \mathfrak {M}_{g,n}$
, we get the usual gluing maps
$\overline {\mathcal {M}}_{g,n} \subset \mathfrak {M}_{g,n}$
, we get the usual gluing maps
Note that unless
![]() $\Gamma $
is stable, the left-hand side is empty.
$\Gamma $
is stable, the left-hand side is empty.
On the other hand, given
![]() $m \geq 0$
, we have the forgetful morphism
$m \geq 0$
, we have the forgetful morphism
Since the curve C remains prestable after forgetting a subset of the markings, there is no stabilization procedure in the morphism
![]() $F_m$
, and the underlying curve remains unchanged.
$F_m$
, and the underlying curve remains unchanged.
Lemma 2.1. The morphism
![]() $F_m$
is smooth and representable of relative dimension m, and the collection
$F_m$
is smooth and representable of relative dimension m, and the collection
forms a smooth and representable cover of
![]() $\mathfrak {M}_{g,n}$
. The complement of the image of
$\mathfrak {M}_{g,n}$
. The complement of the image of
![]() $\overline {\mathcal {M}}_{g,n+m}$
under
$\overline {\mathcal {M}}_{g,n+m}$
under
![]() $F_m$
in
$F_m$
in
![]() $\mathfrak {M}_{g,n}$
has codimension
$\mathfrak {M}_{g,n}$
has codimension
![]() $\lfloor \frac {m}{2} \rfloor +1$
, except for finitely many m in the unstable setting
$\lfloor \frac {m}{2} \rfloor +1$
, except for finitely many m in the unstable setting
![]() $2g-2+n \leq 0$
.Footnote
8
$2g-2+n \leq 0$
.Footnote
8
Proof. Except for the statement about the codimension of the complement of the image, this is [Reference BehrendBeh97, Proposition 2]. To show the formula for the codimension, observe on the one hand that in a prestable graph
![]() $\Gamma $
, every unstable vertex can be stabilized by adding at most two legs. Conversely, consider the prestable graph
$\Gamma $
, every unstable vertex can be stabilized by adding at most two legs. Conversely, consider the prestable graph
![]() $\Gamma _0$
formed by a central vertex of genus g with all n legs, connected via single edges to c outlying vertices of genus
$\Gamma _0$
formed by a central vertex of genus g with all n legs, connected via single edges to c outlying vertices of genus
![]() $0$
with no legs. Then
$0$
with no legs. Then
![]() $\Gamma _0$
belongs to a codimension c stratum, and we need precisely
$\Gamma _0$
belongs to a codimension c stratum, and we need precisely
![]() $2c$
additional legs to stabilize it. Thus the stratum of
$2c$
additional legs to stabilize it. Thus the stratum of
![]() $\mathfrak {M}_{g,n}$
associated to
$\mathfrak {M}_{g,n}$
associated to
![]() $\Gamma _0$
lies in the complement of
$\Gamma _0$
lies in the complement of
![]() $F(\overline {\mathcal {M}}_{g,n+m})$
if and only if
$F(\overline {\mathcal {M}}_{g,n+m})$
if and only if
![]() $c\geq \lfloor \frac {m}{2} \rfloor +1$
. The finitely many exceptions in the unstable range arise from the fact that the central vertex of
$c\geq \lfloor \frac {m}{2} \rfloor +1$
. The finitely many exceptions in the unstable range arise from the fact that the central vertex of
![]() $\Gamma _0$
is not stable if
$\Gamma _0$
is not stable if
![]() $2g-2+n+c<0$
.
$2g-2+n+c<0$
.
Let
![]() $\mathrm {st}_m(\Gamma )$
be the set of stable graphs
$\mathrm {st}_m(\Gamma )$
be the set of stable graphs
![]() $\Gamma '$
in genus g with
$\Gamma '$
in genus g with
![]() $n+m$
markings obtained from a prestable graph
$n+m$
markings obtained from a prestable graph
![]() $\Gamma $
of genus g with n legs by adding m additional legs, labeled
$\Gamma $
of genus g with n legs by adding m additional legs, labeled
![]() $n+1, \ldots , n+m$
, at vertices of
$n+1, \ldots , n+m$
, at vertices of
![]() $\Gamma $
. As explained above, for a fixed prestable graph
$\Gamma $
. As explained above, for a fixed prestable graph
![]() $\Gamma $
, the set
$\Gamma $
, the set
![]() $\mathrm {st}_m(\Gamma )$
starts being nonempty for m sufficiently large.
$\mathrm {st}_m(\Gamma )$
starts being nonempty for m sufficiently large.
Given
![]() $\Gamma ' \in \mathrm {st}_m(\Gamma )$
, there is a natural map
$\Gamma ' \in \mathrm {st}_m(\Gamma )$
, there is a natural map
that is just the product of forgetful maps
![]() $F_{m_v} : \overline {\mathcal {M}}_{g(v),n(v)+m_v} \to \mathfrak {M}_{g(v),n(v)}$
for each
$F_{m_v} : \overline {\mathcal {M}}_{g(v),n(v)+m_v} \to \mathfrak {M}_{g(v),n(v)}$
for each
![]() $v \in V(\Gamma )=V(\Gamma ')$
.
$v \in V(\Gamma )=V(\Gamma ')$
.
Lemma 2.2. For every prestable graph
![]() $\Gamma $
in genus g with n markings and every
$\Gamma $
in genus g with n markings and every
![]() $m \geq 0$
, there is a fibre diagram
$m \geq 0$
, there is a fibre diagram

In particular, the map
![]() $\xi _{\Gamma }: \mathfrak {M}_{\Gamma } \to \mathfrak {M}_{g,n}$
is representable, proper and a local complete intersection.
$\xi _{\Gamma }: \mathfrak {M}_{\Gamma } \to \mathfrak {M}_{g,n}$
is representable, proper and a local complete intersection.
Proof. An object of the fibre product of
![]() $\mathfrak {M}_{\Gamma }$
with
$\mathfrak {M}_{\Gamma }$
with
![]() $\overline {\mathcal {M}}_{g,n+m}$
over a (connected) scheme S is given by
$\overline {\mathcal {M}}_{g,n+m}$
over a (connected) scheme S is given by
-
○ a collection of families
 $(C_v, (p_h)_{h \in H(v)})$
of prestable curves over S for each
$(C_v, (p_h)_{h \in H(v)})$
of prestable curves over S for each
 $v \in V(\Gamma )$
,
$v \in V(\Gamma )$
, -
○ a family
 $(C',p^{\prime }_1, \ldots , p^{\prime }_n, q^{\prime }_1, \ldots , q^{\prime }_m)$
of stable curves over S,
$(C',p^{\prime }_1, \ldots , p^{\prime }_n, q^{\prime }_1, \ldots , q^{\prime }_m)$
of stable curves over S, -
○ an isomorphism (of families of prestable curves)
satisfying $$\begin{align*}\varphi: C=\coprod_v C_v / (p_h \sim p_{h'}, (h,h') \in E(\Gamma)) \to C' \end{align*}$$
$$\begin{align*}\varphi: C=\coprod_v C_v / (p_h \sim p_{h'}, (h,h') \in E(\Gamma)) \to C' \end{align*}$$
 $\varphi (p_i)=p_i'$
.
$\varphi (p_i)=p_i'$
.
By the assumption that S is connected, for each
![]() $j=1, \ldots , m$
, there exists a unique
$j=1, \ldots , m$
, there exists a unique
![]() $v=v(j) \in V(\Gamma )$
such that
$v=v(j) \in V(\Gamma )$
such that
![]() $q^{\prime }_j \in \varphi (C_v)$
at each point of S. This uses that via
$q^{\prime }_j \in \varphi (C_v)$
at each point of S. This uses that via
![]() $\varphi $
, the smooth unmarked points of
$\varphi $
, the smooth unmarked points of
![]() $C_v$
(
$C_v$
(
![]() $v \in V(\Gamma )$
) form a disjoint open cover of the smooth unmarked points of
$v \in V(\Gamma )$
) form a disjoint open cover of the smooth unmarked points of
![]() $(C',p_1, \ldots , p_n)$
in which
$(C',p_1, \ldots , p_n)$
in which
![]() $q^{\prime }_j$
is always contained.
$q^{\prime }_j$
is always contained.
But for
![]() $j,v$
as above, we obtain a section
$j,v$
as above, we obtain a section
![]() $q_j=\varphi ^{-1} \circ q_j' : S \to C_v$
landing in the smooth unmarked locus of
$q_j=\varphi ^{-1} \circ q_j' : S \to C_v$
landing in the smooth unmarked locus of
![]() $C_v$
. Thus for every
$C_v$
. Thus for every
![]() $v \in V(\Gamma )$
, this allows us to define a family
$v \in V(\Gamma )$
, this allows us to define a family
of prestable curves over S. From the fact that
![]() $(C',p^{\prime }_1, \ldots , p^{\prime }_n,q^{\prime }_1, \ldots , q^{\prime }_m)$
is a family of stable curves, it follows that the family in equation (6) is actually a family of stable curves. Then one sees that the collection
$(C',p^{\prime }_1, \ldots , p^{\prime }_n,q^{\prime }_1, \ldots , q^{\prime }_m)$
is a family of stable curves, it follows that the family in equation (6) is actually a family of stable curves. Then one sees that the collection
![]() $({\widehat {C}}_v)_{v \in V(\Gamma ')}$
is exactly an S-point of one of the spaces
$({\widehat {C}}_v)_{v \in V(\Gamma ')}$
is exactly an S-point of one of the spaces
![]() $\overline {\mathcal {M}}_{\Gamma '}$
for the suitable
$\overline {\mathcal {M}}_{\Gamma '}$
for the suitable
![]() $\Gamma ' \in \mathrm {st}_m(\Gamma )$
for which the marking
$\Gamma ' \in \mathrm {st}_m(\Gamma )$
for which the marking
![]() $q_j$
is added at the vertex
$q_j$
is added at the vertex
![]() $v(j) \in V(\Gamma ')=V(\Gamma )$
.
$v(j) \in V(\Gamma ')=V(\Gamma )$
.
The above operations define a map from
![]() $\mathfrak {M}_{\Gamma } \times _{\mathfrak {M}_{g,n}} \overline {\mathcal {M}}_{g,n+m}$
to the disjoint union of the
$\mathfrak {M}_{\Gamma } \times _{\mathfrak {M}_{g,n}} \overline {\mathcal {M}}_{g,n+m}$
to the disjoint union of the
![]() $\overline {\mathcal {M}}_{\Gamma '}$
and clearly this disjoint union also maps to the fibre product using the maps
$\overline {\mathcal {M}}_{\Gamma '}$
and clearly this disjoint union also maps to the fibre product using the maps
![]() $F_{\Gamma ' \to \Gamma }$
and
$F_{\Gamma ' \to \Gamma }$
and
![]() $\xi _{\Gamma '}$
. One verifies that these are inverse isomorphisms.
$\xi _{\Gamma '}$
. One verifies that these are inverse isomorphisms.
Since being proper and being a local complete intersection is local on the target, and since the maps
![]() $F_m$
form a smooth cover of
$F_m$
form a smooth cover of
![]() $\mathfrak {M}_{g,n}$
, these properties of
$\mathfrak {M}_{g,n}$
, these properties of
![]() $\xi _{\Gamma }$
follow from the corresponding properties of the maps
$\xi _{\Gamma }$
follow from the corresponding properties of the maps
![]() $\xi _{\Gamma '}|_{\overline {\mathcal {M}}_{\Gamma '}}$
.
$\xi _{\Gamma '}|_{\overline {\mathcal {M}}_{\Gamma '}}$
.
Later we will need some stronger statements about the locus of curves whose prestable graph is exactly a given graph
![]() $\Gamma $
. This locus is a locally closed substack
$\Gamma $
. This locus is a locally closed substack
![]() $\mathfrak {M}^{\Gamma }$
of
$\mathfrak {M}^{\Gamma }$
of
![]() $\mathfrak {M}_{g,n}$
whose geometric points are precisely the curves
$\mathfrak {M}_{g,n}$
whose geometric points are precisely the curves
![]() $(C,p_1, \ldots , p_n)$
with prestable graph isomorphic to
$(C,p_1, \ldots , p_n)$
with prestable graph isomorphic to
![]() $\Gamma $
. However, since a family of prestable curves over an arbitrary base does not in general have a well-defined prestable graph, this definition is slightly tricky to write down in a functorial way. Thus we approach the definition from a different angle and then show that it defines the desired locus.
$\Gamma $
. However, since a family of prestable curves over an arbitrary base does not in general have a well-defined prestable graph, this definition is slightly tricky to write down in a functorial way. Thus we approach the definition from a different angle and then show that it defines the desired locus.
Definition 2.3. Let
![]() $\Gamma $
be a prestable graph in genus g with n markings, and let e be the number of edges of
$\Gamma $
be a prestable graph in genus g with n markings, and let e be the number of edges of
![]() $\Gamma $
. Then we define
$\Gamma $
. Then we define
where
![]() $\mathrm {im}$
denotes the stack theoretic image and the union goes over prestable graphs
$\mathrm {im}$
denotes the stack theoretic image and the union goes over prestable graphs
![]() $\Gamma '$
with precisely
$\Gamma '$
with precisely
![]() $e+1$
edges.
$e+1$
edges.
By definition, we have that
![]() $\mathfrak {M}^{\Gamma }$
is a locally closed substack of
$\mathfrak {M}^{\Gamma }$
is a locally closed substack of
![]() $\mathfrak {M}_{g,n}$
. In the following lemma, we check that its geometric points are as desired.
$\mathfrak {M}_{g,n}$
. In the following lemma, we check that its geometric points are as desired.
Lemma 2.4. The geometric points of
![]() $\mathfrak {M}^{\Gamma }$
are precisely the
$\mathfrak {M}^{\Gamma }$
are precisely the
![]() $(C,p_1, \ldots , p_n)$
with prestable graph isomorphic to
$(C,p_1, \ldots , p_n)$
with prestable graph isomorphic to
![]() $\Gamma $
.
$\Gamma $
.
Proof. First we note that since
![]() $\xi _{\Gamma }$
is proper, it is surjective onto its image. Then, on the one hand, each
$\xi _{\Gamma }$
is proper, it is surjective onto its image. Then, on the one hand, each
![]() $(C,p_1, \ldots , p_n)$
with prestable graph isomorphic to
$(C,p_1, \ldots , p_n)$
with prestable graph isomorphic to
![]() $\Gamma $
is in
$\Gamma $
is in
![]() $\mathfrak {M}^{\Gamma }$
, since it is in the image of
$\mathfrak {M}^{\Gamma }$
, since it is in the image of
![]() $\xi _{\Gamma }$
but cannot be in the image of a gluing map for a graph
$\xi _{\Gamma }$
but cannot be in the image of a gluing map for a graph
![]() $\Gamma '$
with more than e edges (since its number of nodes is precisely e). Conversely, let
$\Gamma '$
with more than e edges (since its number of nodes is precisely e). Conversely, let
![]() $(C_v)_v = (C_v,(p_h)_{h\in H(v)})_{v \in V(\Gamma )} \in \mathfrak {M}_{\Gamma }$
be a geometric point. Then if all
$(C_v)_v = (C_v,(p_h)_{h\in H(v)})_{v \in V(\Gamma )} \in \mathfrak {M}_{\Gamma }$
be a geometric point. Then if all
![]() $C_v$
are smooth, its image
$C_v$
are smooth, its image
![]() $\xi _{\Gamma }((C_v)_v)$
has prestable graph
$\xi _{\Gamma }((C_v)_v)$
has prestable graph
![]() $\Gamma $
. On the other hand, if any of the
$\Gamma $
. On the other hand, if any of the
![]() $C_v$
are not smooth, then the prestable graph of
$C_v$
are not smooth, then the prestable graph of
![]() $\xi _{\Gamma }((C_v)_v)$
has at least
$\xi _{\Gamma }((C_v)_v)$
has at least
![]() $e+1$
edges. By contracting all but
$e+1$
edges. By contracting all but
![]() $e+1$
of them, we obtain one of the prestable graphs
$e+1$
of them, we obtain one of the prestable graphs
![]() $\Gamma '$
in the definition of
$\Gamma '$
in the definition of
![]() $\mathfrak {M}^{\Gamma }$
, and it is easy to see that
$\mathfrak {M}^{\Gamma }$
, and it is easy to see that
![]() $\xi _{\Gamma }((C_v)_v)$
is then in the image of
$\xi _{\Gamma }((C_v)_v)$
is then in the image of
![]() $\xi _{\Gamma '}$
.
$\xi _{\Gamma '}$
.
We have the following neat description of
![]() $\mathfrak {M}^{\Gamma }$
, which is a generalization of [Reference FulghesuFul10b, Lemma 5.1]. For the statement, let
$\mathfrak {M}^{\Gamma }$
, which is a generalization of [Reference FulghesuFul10b, Lemma 5.1]. For the statement, let
be the open substack where the curve C is smooth. For
![]() $g,n$
in the stable range, this is the usual stack
$g,n$
in the stable range, this is the usual stack
![]() $\mathcal {M}_{g,n}$
of smooth curves, but since the latter might be defined to be empty for
$\mathcal {M}_{g,n}$
of smooth curves, but since the latter might be defined to be empty for
![]() $2g-2+n<0$
, we use the notation
$2g-2+n<0$
, we use the notation
![]() $\mathfrak {M}_{g,n}^{\mathrm {sm}}$
for clarity.
$\mathfrak {M}_{g,n}^{\mathrm {sm}}$
for clarity.
Proposition 2.5. For a prestable graph
![]() $\Gamma $
, consider the open substack
$\Gamma $
, consider the open substack
Then the restriction of the gluing map
![]() $\xi _{\Gamma }$
to
$\xi _{\Gamma }$
to
![]() $\mathfrak {M}_{\Gamma }^{\mathrm {sm}}$
factors through
$\mathfrak {M}_{\Gamma }^{\mathrm {sm}}$
factors through
![]() $\mathfrak {M}^{\Gamma }$
, and it is invariant under the natural action of
$\mathfrak {M}^{\Gamma }$
, and it is invariant under the natural action of
![]() $\mathrm {Aut}(\Gamma )$
. The induced map
$\mathrm {Aut}(\Gamma )$
. The induced map
from the quotient stackFootnote
9
of
![]() $\mathfrak {M}_{\Gamma }$
by
$\mathfrak {M}_{\Gamma }$
by
![]() $\mathrm {Aut}(\Gamma )$
is an isomorphism.
$\mathrm {Aut}(\Gamma )$
is an isomorphism.
Proof. For each point
![]() $(C_v)_v = (C_v,(p_h)_{h\in H(v)})_{v \in V(\Gamma )} \in \mathfrak {M}_{\Gamma }^{\mathrm {sm}}$
, the stabilizer
$(C_v)_v = (C_v,(p_h)_{h\in H(v)})_{v \in V(\Gamma )} \in \mathfrak {M}_{\Gamma }^{\mathrm {sm}}$
, the stabilizer
![]() $\mathrm {Aut}(\Gamma )_{(C_v)_v}$
under the action of
$\mathrm {Aut}(\Gamma )_{(C_v)_v}$
under the action of
![]() $\mathrm {Aut}(\Gamma )$
is the set of automorphisms of
$\mathrm {Aut}(\Gamma )$
is the set of automorphisms of
![]() $\Gamma $
such that there exist compatible isomorphisms of the curves
$\Gamma $
such that there exist compatible isomorphisms of the curves
![]() $(C_v,(p_h)_{h\in H(v)})$
. The stabilizer group of
$(C_v,(p_h)_{h\in H(v)})$
. The stabilizer group of
![]() $[(C_v)_v] \in \mathfrak {M}_{\Gamma }^{\mathrm {sm}} / \mathrm {Aut}(\Gamma )$
is then an extension of the product of the automorphism groups of the
$[(C_v)_v] \in \mathfrak {M}_{\Gamma }^{\mathrm {sm}} / \mathrm {Aut}(\Gamma )$
is then an extension of the product of the automorphism groups of the
![]() $(C_v,(p_h)_{h\in H(v)})$
by the group
$(C_v,(p_h)_{h\in H(v)})$
by the group
![]() $\mathrm {Aut}(\Gamma )_{(C_v)_v}$
.
$\mathrm {Aut}(\Gamma )_{(C_v)_v}$
.
On the other hand, for the curve
![]() $(C,p_1,\ldots ,p_n)$
obtained from
$(C,p_1,\ldots ,p_n)$
obtained from
![]() $(C_v)_v$
by gluing and an element
$(C_v)_v$
by gluing and an element
![]() $\sigma \in \mathrm {Aut}(\Gamma )_{(C_v)_v}$
, the isomorphisms between the curves
$\sigma \in \mathrm {Aut}(\Gamma )_{(C_v)_v}$
, the isomorphisms between the curves
![]() $C_v$
that are compatible with
$C_v$
that are compatible with
![]() $\sigma $
can be glued to an automorphism of
$\sigma $
can be glued to an automorphism of
![]() $(C,p_1,\ldots ,p_n)$
. From this it follows that there exists an exact sequence
$(C,p_1,\ldots ,p_n)$
. From this it follows that there exists an exact sequence
From this sequence we see that
![]() $\mathrm {Aut}(C,p_1,\ldots ,p_n)$
is precisely the group extension defining the stabilizer of
$\mathrm {Aut}(C,p_1,\ldots ,p_n)$
is precisely the group extension defining the stabilizer of
![]() $[(C_v)_v] \in \mathfrak {M}_{\Gamma }^{\mathrm {sm}} / \mathrm {Aut}(\Gamma )$
, and hence
$[(C_v)_v] \in \mathfrak {M}_{\Gamma }^{\mathrm {sm}} / \mathrm {Aut}(\Gamma )$
, and hence
![]() $\xi _{\Gamma }$
induces an isomorphism of each stabilizer. Thus the morphism
$\xi _{\Gamma }$
induces an isomorphism of each stabilizer. Thus the morphism
![]() $\xi _{\Gamma }$
in equation (7) is representable. It is easy to check that it is bijective on geometric points and it is separated by similar argument as in Lemma 2.2. So by [Sta20, 0DUD] it is enough to show that
$\xi _{\Gamma }$
in equation (7) is representable. It is easy to check that it is bijective on geometric points and it is separated by similar argument as in Lemma 2.2. So by [Sta20, 0DUD] it is enough to show that
![]() $\xi _{\Gamma }$
is an étale morphism to conclude that it is an isomorphism.
$\xi _{\Gamma }$
is an étale morphism to conclude that it is an isomorphism.
Consider the atlas
![]() $F_m$
restricted to
$F_m$
restricted to
![]() $\mathfrak {M}^{\Gamma }$
. Since being étale is local on the target, it is enough to show that
$\mathfrak {M}^{\Gamma }$
. Since being étale is local on the target, it is enough to show that
![]() $\xi _{\Gamma }$
is étale on each atlas. On each atlas, the dimension of the fibre is constantly zero. The domain of
$\xi _{\Gamma }$
is étale on each atlas. On each atlas, the dimension of the fibre is constantly zero. The domain of
![]() $\xi _{\Gamma }$
is smooth because it can be written as a quotient of a smooth algebraic space by a group scheme ([Sta20, 0DLS]). Following a slight variation of the proof of [Reference Arbarello, Cornalba and GriffithsACG11, Proposition 10.11], the stack
$\xi _{\Gamma }$
is smooth because it can be written as a quotient of a smooth algebraic space by a group scheme ([Sta20, 0DLS]). Following a slight variation of the proof of [Reference Arbarello, Cornalba and GriffithsACG11, Proposition 10.11], the stack
![]() $\mathfrak {M}^{\Gamma }$
is also smooth. Since the domain and the target of
$\mathfrak {M}^{\Gamma }$
is also smooth. Since the domain and the target of
![]() $\xi _{\Gamma }$
are smooth, the ‘miracle flatness’ ([Sta20, 00R3]) implies that
$\xi _{\Gamma }$
are smooth, the ‘miracle flatness’ ([Sta20, 00R3]) implies that
![]() $\xi _{\Gamma }$
is flat. Furthermore, the morphism is smooth because it is flat, and each geometric fibre is smooth. Smooth and quasi-finite morphisms are étale, and hence
$\xi _{\Gamma }$
is flat. Furthermore, the morphism is smooth because it is flat, and each geometric fibre is smooth. Smooth and quasi-finite morphisms are étale, and hence
![]() $\xi _{\Gamma }$
is an isomorphism.
$\xi _{\Gamma }$
is an isomorphism.
2.2
 $\mathcal {A}$
-valued prestable curves
$\mathcal {A}$
-valued prestable curves
For each
![]() $g,n$
, there exists the universal curve
$g,n$
, there exists the universal curve
![]() $\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
. For later applications, it will be necessary to compute with tautological classes on
$\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
. For later applications, it will be necessary to compute with tautological classes on
![]() $\mathfrak {C}_{g,n}$
(and tautological classes on the universal curve over
$\mathfrak {C}_{g,n}$
(and tautological classes on the universal curve over
![]() $\mathfrak {C}_{g,n}$
, etc.). For the moduli spaces of stable curves, a separate theory is not necessary because the universal curve over
$\mathfrak {C}_{g,n}$
, etc.). For the moduli spaces of stable curves, a separate theory is not necessary because the universal curve over
![]() $\overline {\mathcal {M}}_{g,n}$
is given by the forgetful map
$\overline {\mathcal {M}}_{g,n}$
is given by the forgetful map
![]() $\overline {\mathcal {M}}_{g,n+1} \to \overline {\mathcal {M}}_{g,n}$
. The same is not true for
$\overline {\mathcal {M}}_{g,n+1} \to \overline {\mathcal {M}}_{g,n}$
. The same is not true for
![]() $\mathfrak {M}_{g,n}$
. Indeed, in Lemma 2.1, we saw that the forgetful morphism
$\mathfrak {M}_{g,n}$
. Indeed, in Lemma 2.1, we saw that the forgetful morphism
![]() $\mathfrak {M}_{g,n+1} \to \mathfrak {M}_{g,n}$
is smooth, so it cannot be the universal curve over
$\mathfrak {M}_{g,n+1} \to \mathfrak {M}_{g,n}$
is smooth, so it cannot be the universal curve over
![]() $\mathfrak {M}_{g,n}$
. In this section, we put an additional structure on prestable curves, called the
$\mathfrak {M}_{g,n}$
. In this section, we put an additional structure on prestable curves, called the
![]() $\mathcal {A}$
-value, which allows us to give a modular interpretation of the universal curve as a stack of
$\mathcal {A}$
-value, which allows us to give a modular interpretation of the universal curve as a stack of
![]() $(n+1)$
-pointed curves with additional structure. This realization will be convenient to compute tautological classes on
$(n+1)$
-pointed curves with additional structure. This realization will be convenient to compute tautological classes on
![]() $\mathfrak {C}_{g,n}$
.
$\mathfrak {C}_{g,n}$
.
So let us start by recalling the notion of prestable curves with values in a semigroup
![]() $\mathcal {A}$
from [Reference CostelloCos06]. In what follows, let
$\mathcal {A}$
from [Reference CostelloCos06]. In what follows, let
![]() $\mathcal {A}$
be a commutative semigroup with unit
$\mathcal {A}$
be a commutative semigroup with unit
such that
-
○
 $\mathcal {A}$
has indecomposable zero: that is, for
$\mathcal {A}$
has indecomposable zero: that is, for
 $x,y \in \mathcal {A}$
, we have
$x,y \in \mathcal {A}$
, we have
 implies
implies
 ,
,
 ,
, -
○
 $\mathcal {A}$
has finite decomposition: that is, for
$\mathcal {A}$
has finite decomposition: that is, for
 $a \in \mathcal {A}$
the set is finite.
$a \in \mathcal {A}$
the set is finite. $$ \begin{align*}\{(a_1,a_2) \in \mathcal{A} \times \mathcal{A} : a_1 + a_2 =a\}\end{align*} $$
$$ \begin{align*}\{(a_1,a_2) \in \mathcal{A} \times \mathcal{A} : a_1 + a_2 =a\}\end{align*} $$
Classical examples include
or
![]() $\mathcal {A}=\mathbb {N}$
, but later we are going to work with
$\mathcal {A}=\mathbb {N}$
, but later we are going to work with
Fixing
![]() $\mathcal {A}$
and an element
$\mathcal {A}$
and an element
![]() $a \in \mathcal {A}$
, Behrend-Manin [Reference Behrend and ManinBM96] and Costello [Reference CostelloCos06] define an algebraic stack
$a \in \mathcal {A}$
, Behrend-Manin [Reference Behrend and ManinBM96] and Costello [Reference CostelloCos06] define an algebraic stack
![]() $\mathfrak {M}_{g,n,a}$
. A geometric point corresponds to a prestable curve
$\mathfrak {M}_{g,n,a}$
. A geometric point corresponds to a prestable curve
![]() $(C,p_1, \ldots , p_n)$
together with a map
$(C,p_1, \ldots , p_n)$
together with a map
![]() $C_v \mapsto a_{C_v}$
from the set of irreducible components
$C_v \mapsto a_{C_v}$
from the set of irreducible components
![]() $C_v$
of the normalization of C to
$C_v$
of the normalization of C to
![]() $\mathcal {A}$
such that the sum of all
$\mathcal {A}$
such that the sum of all
![]() $a_{C_v}$
equals a. The curve must satisfy the stability condition that for each
$a_{C_v}$
equals a. The curve must satisfy the stability condition that for each
![]() $C_v$
either
$C_v$
either
![]() or that
or that
![]() $C_v$
is stable, in the sense that for
$C_v$
is stable, in the sense that for
![]() $g(C_v)=0$
it carries three special points and for
$g(C_v)=0$
it carries three special points and for
![]() $g(C_v)=1$
it carries at least one special point. Over an arbitrary base scheme, the definition of
$g(C_v)=1$
it carries at least one special point. Over an arbitrary base scheme, the definition of
![]() $\mathcal {A}$
-valued stable curves needs extra care; see [Reference CostelloCos06, p.569] for details. As an example, for any
$\mathcal {A}$
-valued stable curves needs extra care; see [Reference CostelloCos06, p.569] for details. As an example, for any
![]() $\mathcal {A}$
as above and
$\mathcal {A}$
as above and
![]() , we obtain
, we obtain
![]() .
.
Our main motivation for considering the moduli spaces
![]() $\mathfrak {M}_{g,n,a}$
is the fact that we have a forgetful morphism
$\mathfrak {M}_{g,n,a}$
is the fact that we have a forgetful morphism
![]() $\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
making
$\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
making
![]() $\mathfrak {M}_{g,n+1,a}$
the universal curve over
$\mathfrak {M}_{g,n+1,a}$
the universal curve over
![]() $\mathfrak {M}_{g,n,a}$
. The image of a point
$\mathfrak {M}_{g,n,a}$
. The image of a point
under
![]() $\pi $
is formed by first forgetting the marked point
$\pi $
is formed by first forgetting the marked point
![]() $p_{n+1}$
. Then if the component
$p_{n+1}$
. Then if the component
![]() $C_v$
of C containing
$C_v$
of C containing
![]() $p_{n+1}$
becomes unstable,Footnote
10
the component
$p_{n+1}$
becomes unstable,Footnote
10
the component
![]() $C_v$
of C is contracted. With this notation in place, we summarize the relevant properties of
$C_v$
of C is contracted. With this notation in place, we summarize the relevant properties of
![]() $\mathfrak {M}_{g,n,a}$
from [Reference CostelloCos06].
$\mathfrak {M}_{g,n,a}$
from [Reference CostelloCos06].
Proposition 2.6. The stack
![]() $\mathfrak {M}_{g,n,a}$
is a smooth, algebraic stack, locally of finite type and the morphism
$\mathfrak {M}_{g,n,a}$
is a smooth, algebraic stack, locally of finite type and the morphism
![]() $\mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n}$
forgetting the value in
$\mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n}$
forgetting the value in
![]() $\mathcal {A}$
is étale and relatively a scheme of finite type. The universal curve over
$\mathcal {A}$
is étale and relatively a scheme of finite type. The universal curve over
![]() $\mathfrak {M}_{g,n,a}$
is given by the forgetful morphism
$\mathfrak {M}_{g,n,a}$
is given by the forgetful morphism
![]() $\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
.
$\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
.
Proof. See Proposition 2.0.2 and 2.1.1 from [Reference CostelloCos06].
The fact that the universal curve is given by a moduli space of curves with an extra marked point turns out to be very convenient. Indeed, as discussed above, this is not the case for the forgetful morphism
![]() $\mathfrak {M}_{g,n+1} \to \mathfrak {M}_{g,n}$
. It is easy to identify
$\mathfrak {M}_{g,n+1} \to \mathfrak {M}_{g,n}$
. It is easy to identify
![]() $\mathfrak {M}_{g,n+1}$
as the open substack
$\mathfrak {M}_{g,n+1}$
as the open substack
![]() $\mathfrak {M}_{g,n+1} \subset \mathfrak {C}_{g,n}$
given as the complement of the set of markings and nodes.
$\mathfrak {M}_{g,n+1} \subset \mathfrak {C}_{g,n}$
given as the complement of the set of markings and nodes.
Many other constructions we saw for prestable curves work in the
![]() $\mathcal {A}$
-valued setting. For instance, for
$\mathcal {A}$
-valued setting. For instance, for
![]() $g_1+g_2=g$
,
$g_1+g_2=g$
,
![]() $n_1+n_2=n$
and
$n_1+n_2=n$
and
![]() $a_1, a_2 \in \mathcal {A}$
with
$a_1, a_2 \in \mathcal {A}$
with
![]() $a_1 + a_2 = a$
, we have a gluing morphism
$a_1 + a_2 = a$
, we have a gluing morphism
These gluing maps are again representable, proper and local complete intersections. Indeed, we have a fibre diagram

and the map at the bottom has all these properties by Lemma 2.2. More generally, one defines the notion of an
![]() $\mathcal {A}$
-valued stable graph, and the corresponding gluing map has all the desired properties.
$\mathcal {A}$
-valued stable graph, and the corresponding gluing map has all the desired properties.
The following result allows us to apply the machinery of Costello to the moduli spaces of prestable curves.
Proposition 2.7. Let
with
; then given
![]() $g,n$
, the subset
$g,n$
, the subset
of
![]() $\mathcal {A}$
-valued curves
$\mathcal {A}$
-valued curves
![]() $(C,p_1, \ldots , p_n; (a_{C_v})_v)$
such that one of the values
$(C,p_1, \ldots , p_n; (a_{C_v})_v)$
such that one of the values
![]() $a_{C_v}$
equals
$a_{C_v}$
equals
is closed. Let
be its complement. Then the composition
of the inclusion of
![]() $\mathfrak U_{g,n}$
with the morphism
$\mathfrak U_{g,n}$
with the morphism
forgetting the
![]() $\mathcal {A}$
-values defines an isomorphism
$\mathcal {A}$
-values defines an isomorphism
![]() $\mathfrak {U}_{g,n} \cong \mathfrak {M}_{g,n}$
.
$\mathfrak {U}_{g,n} \cong \mathfrak {M}_{g,n}$
.
Proof. The underlying reason why
![]() $\mathfrak {Z}_{g,n}$
is closed is that
$\mathfrak {Z}_{g,n}$
is closed is that
![]() is indecomposable in
is indecomposable in
![]() $\mathcal {A}$
: given a curve
$\mathcal {A}$
: given a curve
![]() $(C,p_1, \ldots , p_n; (a_{C_v})_v)$
such that some
$(C,p_1, \ldots , p_n; (a_{C_v})_v)$
such that some
![]() , any degeneration of this curve still has some component with value
, any degeneration of this curve still has some component with value
![]() since in a degeneration of
since in a degeneration of
![]() $C_v$
,
$C_v$
,
![]() $a_{C_v}$
must distribute to the components to which
$a_{C_v}$
must distribute to the components to which
![]() $C_v$
degenerates.
$C_v$
degenerates.
More concretely, we can write
![]() $\mathfrak {Z}_{g,n}$
as the union of images of gluing maps
$\mathfrak {Z}_{g,n}$
as the union of images of gluing maps
![]() $\xi _{\Gamma }$
for suitable
$\xi _{\Gamma }$
for suitable
![]() $\mathcal {A}$
-valued prestable graphs
$\mathcal {A}$
-valued prestable graphs
![]() $\Gamma $
. Indeed, we exactly have to remove the images of
$\Gamma $
. Indeed, we exactly have to remove the images of
![]() $\xi _{\Gamma }$
for
$\xi _{\Gamma }$
for
![]() $\Gamma $
of the form
$\Gamma $
of the form

where
![]() $s \geq 1$
,
$s \geq 1$
,
![]() $e_1, \ldots , e_s \in \mathbb {Z}_{>0}$
,
$e_1, \ldots , e_s \in \mathbb {Z}_{>0}$
,
 $$\begin{align*}g_0+g_1+\ldots+g_s=g+\sum_{i=1}^s e_i-1\end{align*}$$
$$\begin{align*}g_0+g_1+\ldots+g_s=g+\sum_{i=1}^s e_i-1\end{align*}$$
and
![]() $I_0 \coprod I_1 \coprod \ldots \coprod I_s = \{1, \ldots , n\}$
. Note that for this locus to be nonempty, we must require
$I_0 \coprod I_1 \coprod \ldots \coprod I_s = \{1, \ldots , n\}$
. Note that for this locus to be nonempty, we must require
![]() $g_0>0$
or
$g_0>0$
or
![]() $|I_0|+\sum _i e_i>2$
.
$|I_0|+\sum _i e_i>2$
.
While the image of each
![]() $\xi _{\Gamma }$
is closed, we use infinitely many of them. But in the open exhaustion of
$\xi _{\Gamma }$
is closed, we use infinitely many of them. But in the open exhaustion of
![]() by the substacks of curves with at most
by the substacks of curves with at most
![]() $\ell $
nodes, each of these open substacks only intersects finitely many of the images of
$\ell $
nodes, each of these open substacks only intersects finitely many of the images of
![]() $\xi _{\Gamma }$
nontrivially, so the union of their images is still closed.
$\xi _{\Gamma }$
nontrivially, so the union of their images is still closed.
The fact that
![]() $\mathfrak U_{g,n} \to \mathfrak {M}_{g,n}$
is an isomorphism can be seen in different ways: its inverse is just given by the functor sending each prestable curve
$\mathfrak U_{g,n} \to \mathfrak {M}_{g,n}$
is an isomorphism can be seen in different ways: its inverse is just given by the functor sending each prestable curve
![]() $(C,p_1, \ldots , p_n)$
to itself with value
$(C,p_1, \ldots , p_n)$
to itself with value
on each component: that is,
Alternatively, one observes that
![]() $\mathfrak U_{g,n} \to \mathfrak {M}_{g,n}$
is étale, representable and a bijection on geometric points.
$\mathfrak U_{g,n} \to \mathfrak {M}_{g,n}$
is étale, representable and a bijection on geometric points.
Corollary 2.8. The universal curve
![]() $\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
is given by the morphism
$\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
is given by the morphism
forgetting the marking
![]() $n+1$
and contracting the component containing it if this component becomes unstable. The
$n+1$
and contracting the component containing it if this component becomes unstable. The
![]() $\mathcal {A}$
-valued prestable graphs
$\mathcal {A}$
-valued prestable graphs
![]() $\Gamma $
appearing in
$\Gamma $
appearing in
![]() $\mathfrak {Z}_{g,n+1}$
but not contained in
$\mathfrak {Z}_{g,n+1}$
but not contained in
![]() $\pi ^{-1}(\mathfrak Z_{g,n})$
are exactly of one of the three following forms:
$\pi ^{-1}(\mathfrak Z_{g,n})$
are exactly of one of the three following forms:
-
○ for
 $i=1, \ldots , n$
, the graphs (9)corresponding to the n sections of the universal curve
$i=1, \ldots , n$
, the graphs (9)corresponding to the n sections of the universal curve
 $\pi : \mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
,
$\pi : \mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
,
-
○ boundary divisors with edge subdivided, inserting a genus zero, value
 vertex carrying
vertex carrying
 $n+1$
where
$n+1$
where
 $g_1+g_2=g$
and corresponding to the locus of nodes inside the universal curve
$g_1+g_2=g$
and corresponding to the locus of nodes inside the universal curve
 $\pi : \mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
.
$\pi : \mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
.
Corollary 2.8 shows that in order to develop the intersection theory of
![]() $\mathfrak {M}_{g,n}$
and
$\mathfrak {M}_{g,n}$
and
![]() $\mathfrak {C}_{g,n}$
, it suffices to consider the general case of the intersection theory of
$\mathfrak {C}_{g,n}$
, it suffices to consider the general case of the intersection theory of
![]() (or even more generally,
(or even more generally,
![]() $\mathfrak {M}_{g,n,a}$
for any semigroup
$\mathfrak {M}_{g,n,a}$
for any semigroup
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $a \in \mathcal {A}$
).
$a \in \mathcal {A}$
).
3 Chow groups and the tautological ring of
 $\mathfrak {M}_{g,n}$
$\mathfrak {M}_{g,n}$
3.1 Definitions
In this paper, we want to study the Chow groups (with
![]() $\mathbb {Q}$
-coefficients) of the stacks
$\mathbb {Q}$
-coefficients) of the stacks
![]() $\mathfrak {M}_{g,n}$
(and, more generally, the stacks
$\mathfrak {M}_{g,n}$
(and, more generally, the stacks
![]() $\mathfrak {M}_{g,n,a}$
for some element
$\mathfrak {M}_{g,n,a}$
for some element
![]() $a \in \mathcal {A}$
in a semigroup
$a \in \mathcal {A}$
in a semigroup
![]() $\mathcal {A}$
).
$\mathcal {A}$
).
To define these Chow groups, recall that in [Reference KreschKre99], Kresch constructed Chow groups
![]() $\mathrm {CH}_*(\mathcal {X})$
for algebraic stacks
$\mathrm {CH}_*(\mathcal {X})$
for algebraic stacks
![]() $\mathcal {X}$
of finite type over a field k. Moreover, there is an intersection product on
$\mathcal {X}$
of finite type over a field k. Moreover, there is an intersection product on
![]() $\mathrm {CH}_*(\mathcal {X})$
when
$\mathrm {CH}_*(\mathcal {X})$
when
![]() $\mathcal {X}$
is smooth and stratified by global quotient stacks
Footnote
11
; see [Reference KreschKre99, Theorem 2.1.12]. This last condition can be checked point-wise: a reduced stack
$\mathcal {X}$
is smooth and stratified by global quotient stacks
Footnote
11
; see [Reference KreschKre99, Theorem 2.1.12]. This last condition can be checked point-wise: a reduced stack
![]() $\mathcal {X}$
is stratified by global quotient stacks if and only if the stabilizers of geometric points of
$\mathcal {X}$
is stratified by global quotient stacks if and only if the stabilizers of geometric points of
![]() $\mathcal {X}$
are affine ([Reference KreschKre99, Proposition 3.5.9]).
$\mathcal {X}$
are affine ([Reference KreschKre99, Proposition 3.5.9]).
Now the spaces
![]() $\mathfrak {M}_{g,n,a}$
are in general not of finite type (only locally of finite type) and so we need to extend the definition of Chow groups above. Assume that
$\mathfrak {M}_{g,n,a}$
are in general not of finite type (only locally of finite type) and so we need to extend the definition of Chow groups above. Assume that
![]() $\mathfrak {M}$
is an algebraic stack, locally of finite type over a field k. Choose a directed systemFootnote
12
$\mathfrak {M}$
is an algebraic stack, locally of finite type over a field k. Choose a directed systemFootnote
12
![]() $(\mathcal {U}_i)_{i \in I}$
of finite type open substacks of
$(\mathcal {U}_i)_{i \in I}$
of finite type open substacks of
![]() $\mathfrak {M}$
whose union is all of
$\mathfrak {M}$
whose union is all of
![]() $\mathfrak {M}$
. Then we set
$\mathfrak {M}$
. Then we set
where for
![]() $\mathcal U_i \subseteq \mathcal U_j$
the transition map
$\mathcal U_i \subseteq \mathcal U_j$
the transition map
![]() $\mathrm {CH}_*(\mathcal U_j) \to \mathrm {CH}_*(\mathcal U_i)$
is given by the restriction to
$\mathrm {CH}_*(\mathcal U_j) \to \mathrm {CH}_*(\mathcal U_i)$
is given by the restriction to
![]() $\mathcal U_i$
. In other words, we have
$\mathcal U_i$
. In other words, we have
We give the details of this definition in Appendix A and show that the Chow groups of locally finite type stacks inherit all the usual properties (e.g., flat pullback, projective pushforward, Chern classes of vector bundles and Gysin pullbacks) of the Chow groups from [Reference KreschKre99]. Moreover, if
![]() $\mathfrak {M}$
is smooth and has affine stabilizer groups at geometric points, the intersection products on the groups
$\mathfrak {M}$
is smooth and has affine stabilizer groups at geometric points, the intersection products on the groups
![]() $\mathrm {CH}_*(\mathcal U_i)$
give rise to an intersection product on
$\mathrm {CH}_*(\mathcal U_i)$
give rise to an intersection product on
![]() $\mathrm {CH}_*(\mathfrak {M})$
. In this case, for
$\mathrm {CH}_*(\mathfrak {M})$
. In this case, for
![]() $\mathfrak {M}$
equidimensional, we often use the cohomological degree convention
$\mathfrak {M}$
equidimensional, we often use the cohomological degree convention
Proposition 3.1. Let
![]() $g,n \geq 0$
, and let
$g,n \geq 0$
, and let
![]() $\mathcal {A}$
be a semigroup with indecomposable zero and finite decomposition as in Section 2.2 and
$\mathcal {A}$
be a semigroup with indecomposable zero and finite decomposition as in Section 2.2 and
![]() $a \in \mathcal {A}$
. Then the stacks
$a \in \mathcal {A}$
. Then the stacks
![]() $\mathfrak {M}_{g,n}$
and
$\mathfrak {M}_{g,n}$
and
![]() $\mathfrak {M}_{g,n,a}$
have well-defined Chow groups
$\mathfrak {M}_{g,n,a}$
have well-defined Chow groups
![]() $\mathrm {CH}_*(\mathfrak {M}_{g,n})$
and
$\mathrm {CH}_*(\mathfrak {M}_{g,n})$
and
![]() $\mathrm {CH}_*(\mathfrak {M}_{g,n,a})$
. For
$\mathrm {CH}_*(\mathfrak {M}_{g,n,a})$
. For
![]() $(g,n) \neq (1,0)$
the stabilizer groups of all geometric points of
$(g,n) \neq (1,0)$
the stabilizer groups of all geometric points of
![]() $\mathfrak {M}_{g,n}$
and
$\mathfrak {M}_{g,n}$
and
![]() $\mathfrak {M}_{g,n,a}$
are affine and so the Chow groups have an intersection product.
$\mathfrak {M}_{g,n,a}$
are affine and so the Chow groups have an intersection product.
Proof. The stacks
![]() $\mathfrak {M}_{g,n}$
and
$\mathfrak {M}_{g,n}$
and
![]() $\mathfrak {M}_{g,n,a}$
are locally of finite type (and smooth) by Proposition 2.6 and thus satisfy the conditions of Definition A.1 from the appendix. For the existence of intersection products, we need to check that geometric points have affine stabilizers. The stabilizer group of such a prestable curve is a finite extension of the automorphism groups of its components. The only non-finite automorphism groups that can occur here are in genus
$\mathfrak {M}_{g,n,a}$
are locally of finite type (and smooth) by Proposition 2.6 and thus satisfy the conditions of Definition A.1 from the appendix. For the existence of intersection products, we need to check that geometric points have affine stabilizers. The stabilizer group of such a prestable curve is a finite extension of the automorphism groups of its components. The only non-finite automorphism groups that can occur here are in genus
![]() $0$
(where they are subgroups of
$0$
(where they are subgroups of
![]() $\mathrm {PGL}_{2}$
and thus affine) and in genus
$\mathrm {PGL}_{2}$
and thus affine) and in genus
![]() $1$
with no special points. Since the prestable curves are assumed to be connected, the last case can only occur for
$1$
with no special points. Since the prestable curves are assumed to be connected, the last case can only occur for
![]() $(g,n)=(1,0)$
.
$(g,n)=(1,0)$
.
Now recall from Definition 1.3 that the tautological rings
![]() $(\mathrm {R}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
are defined as the smallest system of
$(\mathrm {R}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
are defined as the smallest system of
![]() $\mathbb {Q}$
-subalgebras with unit of the Chow rings
$\mathbb {Q}$
-subalgebras with unit of the Chow rings
![]() $(\mathrm {CH}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
closed under taking pushforwards by the natural forgetful and gluing maps.
$(\mathrm {CH}^*(\mathfrak {M}_{g,n,a}))_{g,n,a}$
closed under taking pushforwards by the natural forgetful and gluing maps.
We recall the following particular examples of tautological classes:
Definition 3.2. Let
![]() $\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
be the universal curve over
$\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
be the universal curve over
![]() $\mathfrak {M}_{g,n,a}$
, and for
$\mathfrak {M}_{g,n,a}$
, and for
![]() $i=1, \ldots , n$
, let
$i=1, \ldots , n$
, let
![]() $\sigma _i : \mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n+1,a}$
be the section corresponding to the i-th marked points. Let
$\sigma _i : \mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n+1,a}$
be the section corresponding to the i-th marked points. Let
![]() $\omega _{\pi }$
be the relative canonical line bundle on
$\omega _{\pi }$
be the relative canonical line bundle on
![]() $\mathfrak {M}_{g,n+1,a}$
. Then we define
$\mathfrak {M}_{g,n+1,a}$
. Then we define
and
Definition 3.3. Let
![]() $\Gamma $
be an
$\Gamma $
be an
![]() $\mathcal {A}$
-valued prestable graph in genus g with n markings with total value
$\mathcal {A}$
-valued prestable graph in genus g with n markings with total value
![]() $a \in \mathcal {A}$
. For
$a \in \mathcal {A}$
. For
![]() $\mathfrak {M}_{\Gamma } = \prod _{v \in V(\Gamma )} \mathfrak {M}_{g(v),n(v),a(v)}$
, a decoration
$\mathfrak {M}_{\Gamma } = \prod _{v \in V(\Gamma )} \mathfrak {M}_{g(v),n(v),a(v)}$
, a decoration
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
is an element of
$\Gamma $
is an element of
![]() $\mathrm {CH}^*(\mathfrak {M}_{\Gamma })$
given by a product of
$\mathrm {CH}^*(\mathfrak {M}_{\Gamma })$
given by a product of
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes on the factors
$\psi $
-classes on the factors
![]() $\mathfrak {M}_{g(v),n(v),a(v)}$
of
$\mathfrak {M}_{g(v),n(v),a(v)}$
of
![]() $\mathfrak {M}_{\Gamma }$
. Thus it has the form
$\mathfrak {M}_{\Gamma }$
. Thus it has the form
 $$ \begin{align} \alpha = \prod_{v\in V} \left( \prod_{i \in H(v)} \psi_{v,i}^{a_i} \prod_{a=1}^{m_v} \kappa_{v,a}^{b_{v,a}} \right)\in \mathrm{CH}^*(\mathfrak{M}_{\Gamma}),\end{align} $$
$$ \begin{align} \alpha = \prod_{v\in V} \left( \prod_{i \in H(v)} \psi_{v,i}^{a_i} \prod_{a=1}^{m_v} \kappa_{v,a}^{b_{v,a}} \right)\in \mathrm{CH}^*(\mathfrak{M}_{\Gamma}),\end{align} $$
where
![]() $a_i, b_{v,a}\geq 0$
and
$a_i, b_{v,a}\geq 0$
and
![]() $m_v\geq 0$
are some integers. We define the decorated stratum class
$m_v\geq 0$
are some integers. We define the decorated stratum class
![]() $[\Gamma ,\alpha ]$
as the pushforward
$[\Gamma ,\alpha ]$
as the pushforward
One of the main goals of this section is to show that the set of tautological classes
![]() $\mathrm {R}^*(\mathfrak {M}_{g,n,a}) \subseteq \mathrm {CH}^*(\mathfrak {M}_{g,n,a})$
is the
$\mathrm {R}^*(\mathfrak {M}_{g,n,a}) \subseteq \mathrm {CH}^*(\mathfrak {M}_{g,n,a})$
is the
![]() $\mathbb {Q}$
-linear span of all classes
$\mathbb {Q}$
-linear span of all classes
![]() $[\Gamma ,\alpha ]$
.
$[\Gamma ,\alpha ]$
.
Remark 3.4. We define tautological classes on the spaces
![]() $\mathfrak {M}_{g,n}$
and
$\mathfrak {M}_{g,n}$
and
![]() $\mathfrak {C}_{g,n}$
by seeing these stacks as open subsets of
$\mathfrak {C}_{g,n}$
by seeing these stacks as open subsets of
![]() and
and
![]() for
for
![]() as in Corollary 2.8. Then tautological classes on
as in Corollary 2.8. Then tautological classes on
![]() $\mathfrak {M}_{g,n}$
and
$\mathfrak {M}_{g,n}$
and
![]() $\mathfrak {C}_{g,n}$
are given by the restrictions of tautological classes on
$\mathfrak {C}_{g,n}$
are given by the restrictions of tautological classes on
![]() and
and
![]() .
.
From the point of view of decorated strata classes, note that for
![]() $\mathfrak {M}_{g,n}$
, only
$\mathfrak {M}_{g,n}$
, only
![]() $\mathcal {A}$
-valued prestable graphs where all values are
$\mathcal {A}$
-valued prestable graphs where all values are
![]() can contribute (and these are in natural bijections with prestable graphs without valuation). On the other hand, for
can contribute (and these are in natural bijections with prestable graphs without valuation). On the other hand, for
![]() $\mathfrak {C}_{g,n}$
, we can have vertices v with value
$\mathfrak {C}_{g,n}$
, we can have vertices v with value
![]() contributing nontrivial classes. This happens exactly for the graphs shown in Corollary 2.8, corresponding to the universal sections of
contributing nontrivial classes. This happens exactly for the graphs shown in Corollary 2.8, corresponding to the universal sections of
![]() $\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
and the loci of nodes inside
$\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
and the loci of nodes inside
![]() $\mathfrak {C}_{g,n}$
over boundary strata of
$\mathfrak {C}_{g,n}$
over boundary strata of
![]() $\mathfrak {M}_{g,n}$
.
$\mathfrak {M}_{g,n}$
.
3.2 Intersections and functoriality of tautological classes
In this section, we describe how the classes
![]() $[\Gamma ,\alpha ]$
behave under taking intersections as well as pullbacks and pushforwards under natural gluing, forgetful and stabilization maps.
$[\Gamma ,\alpha ]$
behave under taking intersections as well as pullbacks and pushforwards under natural gluing, forgetful and stabilization maps.
Pushforwards by gluing maps
Pushing forward by gluing maps is by far the easiest operation: given an
![]() $\mathcal {A}$
-valued graph
$\mathcal {A}$
-valued graph
![]() $\Gamma _0$
and classes
$\Gamma _0$
and classes
![]() $[\Gamma _v,\alpha _v] \in \mathrm {R}^*(\mathfrak {M}_{g(v),n(v),a(v)})$
for
$[\Gamma _v,\alpha _v] \in \mathrm {R}^*(\mathfrak {M}_{g(v),n(v),a(v)})$
for
![]() $v \in V(\Gamma _0)$
, the pushforward of the class
$v \in V(\Gamma _0)$
, the pushforward of the class
is given by
![]() $[\Gamma ,\alpha ]$
, where
$[\Gamma ,\alpha ]$
, where
![]() $\Gamma $
is obtained by gluing the
$\Gamma $
is obtained by gluing the
![]() $\Gamma _i$
into the vertices of the outer graph
$\Gamma _i$
into the vertices of the outer graph
![]() $\Gamma _0$
and
$\Gamma _0$
and
![]() $\alpha $
is obtained by combining the decorations
$\alpha $
is obtained by combining the decorations
![]() $\alpha _v$
using that
$\alpha _v$
using that
![]() $V(\Gamma ) = \coprod _{v \in V(\Gamma _0)} V(\Gamma _v)$
.
$V(\Gamma ) = \coprod _{v \in V(\Gamma _0)} V(\Gamma _v)$
.
Pullbacks by gluing maps and intersection products
The next natural question is how a class
![]() $[B,\beta ]$
pulls back along a gluing morphism
$[B,\beta ]$
pulls back along a gluing morphism
![]() $\xi _A$
for an
$\xi _A$
for an
![]() $\mathcal {A}$
-valued graph A. This operation allows a purely combinatorial description, generalizing the description in
$\mathcal {A}$
-valued graph A. This operation allows a purely combinatorial description, generalizing the description in
![]() $\overline {\mathcal {M}}_{g,n}$
from [Reference Graber and PandharipandeGP03] (and already discussed for graphs A with exactly one edge in [Reference CostelloCos06, Section 4]). As combinatorial preparation, we recall the notion of morphisms of
$\overline {\mathcal {M}}_{g,n}$
from [Reference Graber and PandharipandeGP03] (and already discussed for graphs A with exactly one edge in [Reference CostelloCos06, Section 4]). As combinatorial preparation, we recall the notion of morphisms of
![]() $\mathcal {A}$
-valued stable graphs.
$\mathcal {A}$
-valued stable graphs.
Definition 3.5. An A-structure on an
![]() $\mathcal {A}$
-valued prestable graph
$\mathcal {A}$
-valued prestable graph
![]() $\Gamma $
(write
$\Gamma $
(write
![]() $\Gamma \to A$
) is a choice of subgraphs
$\Gamma \to A$
) is a choice of subgraphs
![]() $\Gamma _v$
of
$\Gamma _v$
of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma $
can be constructed by replacing each vertex v of A by the corresponding
$\Gamma $
can be constructed by replacing each vertex v of A by the corresponding
![]() $\mathcal {A}$
-valued graph
$\mathcal {A}$
-valued graph
![]() $\Gamma _v$
. More precisely, the data of
$\Gamma _v$
. More precisely, the data of
![]() $\Gamma \to A$
is given by maps
$\Gamma \to A$
is given by maps
They must satisfy that
![]() $V(\Gamma ) \to V(A)$
is surjective, such that the preimage of
$V(\Gamma ) \to V(A)$
is surjective, such that the preimage of
![]() $v \in V(A)$
are the vertices of a subgraph
$v \in V(A)$
are the vertices of a subgraph
![]() $\Gamma _v$
of
$\Gamma _v$
of
![]() $\Gamma $
with total
$\Gamma $
with total
![]() $\mathcal {A}$
-value
$\mathcal {A}$
-value
![]() $a_v$
. The map
$a_v$
. The map
![]() $H(A) \to H(\Gamma )$
of half-edges in the opposite direction is required to be injective and allows one to see half-edges
$H(A) \to H(\Gamma )$
of half-edges in the opposite direction is required to be injective and allows one to see half-edges
![]() $h \in H(v)$
of A with legs of the graph
$h \in H(v)$
of A with legs of the graph
![]() $\Gamma _v$
. These maps must respect the incidence relation of half-edges and vertices and the pairs of half-edges forming edges. In particular, the injection of half-edges allows us to see the set of edges
$\Gamma _v$
. These maps must respect the incidence relation of half-edges and vertices and the pairs of half-edges forming edges. In particular, the injection of half-edges allows us to see the set of edges
![]() $E(A)$
of A as a subset of the set of edges
$E(A)$
of A as a subset of the set of edges
![]() $E(\Gamma )$
of
$E(\Gamma )$
of
![]() $\Gamma $
(see, e.g., [Reference Schmitt and van ZelmSvZ20, Definition 2.5] for more details in the case of stable graphs).
$\Gamma $
(see, e.g., [Reference Schmitt and van ZelmSvZ20, Definition 2.5] for more details in the case of stable graphs).
Given an A-structure
![]() $\Gamma \to A$
, there exists a gluing morphism
$\Gamma \to A$
, there exists a gluing morphism
For a decoration
![]() $\alpha $
on
$\alpha $
on
![]() $\mathfrak {M}_A$
as in equation (12), it is easy to describe
$\mathfrak {M}_A$
as in equation (12), it is easy to describe
![]() $\xi _{\Gamma \to A}^* \alpha $
using that
$\xi _{\Gamma \to A}^* \alpha $
using that
-
○
 $\xi _{\Gamma \to A}^* \psi _{v,i} = \psi _{w,j}$
if
$\xi _{\Gamma \to A}^* \psi _{v,i} = \psi _{w,j}$
if
 $\Gamma \to A$
maps half-edge i in A to half-edge j in
$\Gamma \to A$
maps half-edge i in A to half-edge j in
 $\Gamma $
,
$\Gamma $
, -
○
 $\xi _{\Gamma \to A}^* \kappa _{v,\ell } = \sum _{w \mapsto v} \kappa _{w,\ell }$
, where the sum goes over vertices w of
$\xi _{\Gamma \to A}^* \kappa _{v,\ell } = \sum _{w \mapsto v} \kappa _{w,\ell }$
, where the sum goes over vertices w of
 $\Gamma $
mapping to the vertex v of A on which
$\Gamma $
mapping to the vertex v of A on which
 $\kappa _{v,\ell }$
lives.
$\kappa _{v,\ell }$
lives.
Both these properties follow immediately from the definitionsFootnote
13
of
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes.
$\psi $
-classes.
Let
![]() $f_A : \Gamma \to A$
,
$f_A : \Gamma \to A$
,
![]() $f_B : \Gamma \to B$
be A and B-structures on the prestable graph
$f_B : \Gamma \to B$
be A and B-structures on the prestable graph
![]() $\Gamma $
. The pair
$\Gamma $
. The pair
![]() $f = (f_A, f_B)$
is called a generic
$f = (f_A, f_B)$
is called a generic
![]() $(A,B)$
-structure
$(A,B)$
-structure
![]() $f=(f_A,f_B)$
on
$f=(f_A,f_B)$
on
![]() $\Gamma $
if every half-edge of
$\Gamma $
if every half-edge of
![]() $\Gamma $
corresponds to a half-edge of A or a half-edge of B. Given a second
$\Gamma $
corresponds to a half-edge of A or a half-edge of B. Given a second
![]() $(A,B)$
-structure
$(A,B)$
-structure
![]() $f'=(f_A': \Gamma ' \to A, f_B': \Gamma ' \to B)$
, an isomorphism from f to
$f'=(f_A': \Gamma ' \to A, f_B': \Gamma ' \to B)$
, an isomorphism from f to
![]() $f'$
is an isomorphism
$f'$
is an isomorphism
![]() $\Gamma \to \Gamma '$
commuting with the maps to
$\Gamma \to \Gamma '$
commuting with the maps to
![]() $A,B$
. Let
$A,B$
. Let
![]() $\mathcal {G}_{A,B}$
be the set of isomorphism classes of prestable graphs
$\mathcal {G}_{A,B}$
be the set of isomorphism classes of prestable graphs
![]() $\Gamma $
together with a generic
$\Gamma $
together with a generic
![]() $(A,B)$
-structures on
$(A,B)$
-structures on
![]() $\Gamma $
.
$\Gamma $
.
Proposition 3.6. Let
![]() $A,B$
be
$A,B$
be
![]() $\mathcal {A}$
-valued prestable graphs for
$\mathcal {A}$
-valued prestable graphs for
![]() $\mathfrak {M}_{g,n,a}$
; then the fibre product of the gluing maps
$\mathfrak {M}_{g,n,a}$
; then the fibre product of the gluing maps
![]() $\xi _A : \mathfrak {M}_A \to \mathfrak {M}_{g,n,a}$
and
$\xi _A : \mathfrak {M}_A \to \mathfrak {M}_{g,n,a}$
and
![]() $\xi _B : \mathfrak {M}_B \to \mathfrak {M}_{g,n,a}$
is given by a disjoint union
$\xi _B : \mathfrak {M}_B \to \mathfrak {M}_{g,n,a}$
is given by a disjoint union

of spaces
![]() $\mathfrak {M}_{\Gamma }$
for the set of isomorphism classes of generic
$\mathfrak {M}_{\Gamma }$
for the set of isomorphism classes of generic
![]() $(A,B)$
-structures on prestable graphs
$(A,B)$
-structures on prestable graphs
![]() $\Gamma $
. The top Chern class of the excess bundle
$\Gamma $
. The top Chern class of the excess bundle
is given by
where the product is over the edges of
![]() $\Gamma $
coming both from edges of A and edges of B in the generic
$\Gamma $
coming both from edges of A and edges of B in the generic
![]() $(A,B)$
-structure.
$(A,B)$
-structure.
Proof. The proof from [Reference Graber and PandharipandeGP03, Proposition 9] of the analogous result for the moduli spaces of stable curves goes through verbatim (see also [Reference Schmitt and van ZelmSvZ20, Section 2] for a more detailed version of the argument).
Using the projection formula, we can then also intersect tautological classes.
Corollary 3.7. Given decorated stratum classes
![]() $[A,\alpha ]$
,
$[A,\alpha ]$
,
![]() $[B,\beta ]$
on
$[B,\beta ]$
on
![]() $\mathfrak {M}_{g,n,a}$
, their product is given by
$\mathfrak {M}_{g,n,a}$
, their product is given by
 $$ \begin{align} [A,\alpha] \cdot [B,\beta] = \sum_{\Gamma \in \mathcal{G}_{A,B}} (\xi_{\Gamma})_* \left(\xi_{\Gamma \to A}^* \alpha \cdot \xi_{\Gamma \to B}^* \beta \cdot c_{\mathrm{top}}(E_{\Gamma}) \right).\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} [A,\alpha] \cdot [B,\beta] = \sum_{\Gamma \in \mathcal{G}_{A,B}} (\xi_{\Gamma})_* \left(\xi_{\Gamma \to A}^* \alpha \cdot \xi_{\Gamma \to B}^* \beta \cdot c_{\mathrm{top}}(E_{\Gamma}) \right).\\[-15pt]\nonumber \end{align} $$
Pushforwards and pullbacks by forgetful maps of points
In this section, we look at the behaviour of tautological classes under the forgetful map
![]() $\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
, which is the universal curve over
$\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
, which is the universal curve over
![]() $\mathfrak {M}_{g,n,a}$
. As such, it is both flat and proper, so we can compute pullbacks as well as pushforwards. We will start with pullbacks.
$\mathfrak {M}_{g,n,a}$
. As such, it is both flat and proper, so we can compute pullbacks as well as pushforwards. We will start with pullbacks.
Proposition 3.8. Given an
![]() $\mathcal {A}$
-valued prestable graph
$\mathcal {A}$
-valued prestable graph
![]() $\Gamma $
for
$\Gamma $
for
![]() $\mathfrak {M}_{g,n,a}$
, we have a commutative diagram
$\mathfrak {M}_{g,n,a}$
, we have a commutative diagram

where the graph
![]() $\widehat \Gamma _v$
is obtained from
$\widehat \Gamma _v$
is obtained from
![]() $\Gamma $
by adding the marking
$\Gamma $
by adding the marking
![]() $n+1$
at vertex v and the map
$n+1$
at vertex v and the map
![]() $\pi _v$
is the identity on the factors of
$\pi _v$
is the identity on the factors of
![]() $\mathfrak {M}_{\widehat \Gamma _v}$
for vertices
$\mathfrak {M}_{\widehat \Gamma _v}$
for vertices
![]() $w \neq v$
and the forgetful map of marking
$w \neq v$
and the forgetful map of marking
![]() $n+1$
at the vertex v. The induced map
$n+1$
at the vertex v. The induced map
satisfies that the fundamental class on the left pushes forward to the fundamental class on the right.
Proof. This follows from the definition of the gluing map
![]() $\xi _{\Gamma }$
: giving the map
$\xi _{\Gamma }$
: giving the map
![]() $\xi _{\Gamma }$
is the same as giving the universal curve over
$\xi _{\Gamma }$
is the same as giving the universal curve over
![]() $\mathfrak {M}_{\Gamma }$
, and this curve is obtained by gluing the universal curves
$\mathfrak {M}_{\Gamma }$
, and this curve is obtained by gluing the universal curves
![]() $\mathfrak {M}_{\widehat \Gamma _v}$
over the various factors along the half-edges connected in
$\mathfrak {M}_{\widehat \Gamma _v}$
over the various factors along the half-edges connected in
![]() $\Gamma $
. The map in equation (18) is obtained by taking, for each edge
$\Gamma $
. The map in equation (18) is obtained by taking, for each edge
![]() $\{h_1,h_2\} \in E(\Gamma )$
the loci inside
$\{h_1,h_2\} \in E(\Gamma )$
the loci inside
![]() $\mathfrak {M}_{\widehat \Gamma _{v_i}}$
, where marking
$\mathfrak {M}_{\widehat \Gamma _{v_i}}$
, where marking
![]() $p_{n+1}$
and marking
$p_{n+1}$
and marking
![]() $q_{h_i}$
are on a contracted component and identifying them. Thus, if
$q_{h_i}$
are on a contracted component and identifying them. Thus, if
![]() $p_{n+1}$
is not on a contracted component, the map is an isomorphism in a neighborhood. Therefore the map in equation (18) is an isomorphism at the general point of each component of the right-hand side, and the fundamental class pushes forward to the fundamental class.
$p_{n+1}$
is not on a contracted component, the map is an isomorphism in a neighborhood. Therefore the map in equation (18) is an isomorphism at the general point of each component of the right-hand side, and the fundamental class pushes forward to the fundamental class.
Corollary 3.9. Given a tautological class
![]() $[\Gamma ,\alpha ]$
, write
$[\Gamma ,\alpha ]$
, write
![]() $\alpha = \prod _{v \in V(\Gamma )} \alpha _v$
with
$\alpha = \prod _{v \in V(\Gamma )} \alpha _v$
with
![]() $\alpha _v$
the factors of
$\alpha _v$
the factors of
![]() $\alpha $
located at vertex v of
$\alpha $
located at vertex v of
![]() $\Gamma $
. Then we have
$\Gamma $
. Then we have
Proof. The class
![]() $[\Gamma ,\alpha ]$
is represented by
$[\Gamma ,\alpha ]$
is represented by
![]() $\xi _{\Gamma *}\left (\alpha \cap \,[\mathfrak {M}_{\Gamma }]\right )$
, where
$\xi _{\Gamma *}\left (\alpha \cap \,[\mathfrak {M}_{\Gamma }]\right )$
, where
![]() $\alpha $
is an operational Chow class in
$\alpha $
is an operational Chow class in
![]() $\mathrm {CH}_{\mathrm {OP}}^*(\mathfrak {M}_{\Gamma })$
. We refer the reader to Appendix C for definitions and properties of these operational classes. By Proposition 3.8, the diagram in equation (17) together with the map in equation (18) satisfies assumptions in Lemma C.8. Therefore the equality follows from Lemma C.8.
$\mathrm {CH}_{\mathrm {OP}}^*(\mathfrak {M}_{\Gamma })$
. We refer the reader to Appendix C for definitions and properties of these operational classes. By Proposition 3.8, the diagram in equation (17) together with the map in equation (18) satisfies assumptions in Lemma C.8. Therefore the equality follows from Lemma C.8.
The above corollary shows that to finish our understanding of pullbacks of tautological classes, it suffices to understand how
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes pull back.
$\psi $
-classes pull back.
Proposition 3.10. For the universal curve morphism
![]() $\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
, we have
$\pi : \mathfrak {M}_{g,n+1,a} \to \mathfrak {M}_{g,n,a}$
, we have
where
![]() $D_{i,n+1} \subset \mathfrak {M}_{g,n+1,a}$
is the image of the section
$D_{i,n+1} \subset \mathfrak {M}_{g,n+1,a}$
is the image of the section
![]() $\sigma _i$
of
$\sigma _i$
of
![]() $\pi $
corresponding to the ith marked point. It can be seen as the tautological class corresponding to the (undecorated) graph in equation (9) above.
$\pi $
corresponding to the ith marked point. It can be seen as the tautological class corresponding to the (undecorated) graph in equation (9) above.
Proof. The statement is a generalization of the classical pullback formulas for
![]() $\overline {\mathcal {M}}_{g,n}$
(which are the case
$\overline {\mathcal {M}}_{g,n}$
(which are the case
). A convenient way to prove it is to use that
To show this, we note that
![]() $\sigma _i$
can be identified with the gluing map
$\sigma _i$
can be identified with the gluing map
where we glue the ith marking on
![]() $\mathfrak {M}_{g,n,a}$
with the marking
$\mathfrak {M}_{g,n,a}$
with the marking
![]() $\bullet $
on
$\bullet $
on
. Then indeed the locus
![]() $D_{i,n+1}$
is the image of the above gluing map (similar to the usual case of stable maps), and equation (21) follows from Corollary 3.7. On the other hand, it can also be seen directly from the fact that
$D_{i,n+1}$
is the image of the above gluing map (similar to the usual case of stable maps), and equation (21) follows from Corollary 3.7. On the other hand, it can also be seen directly from the fact that
![]() $\sigma _i$
is a closed embedding with normal bundle
$\sigma _i$
is a closed embedding with normal bundle
![]() $\sigma _i^*(\omega _{\pi }^{\vee })$
.
$\sigma _i^*(\omega _{\pi }^{\vee })$
.
Now we have a commutative diagram

and the space in the upper left maps birationally to the fibre product of the two forgetful maps. Then

Similarly, using the same diagram, the definition of
![]() $\kappa _a$
and the pullback formula for
$\kappa _a$
and the pullback formula for
![]() $\psi $
, one concludes the pullback formula for
$\psi $
, one concludes the pullback formula for
![]() $\kappa _a$
.
$\kappa _a$
.
We now turn to the question how to push forward tautological classes
![]() $[\Gamma , \alpha ] \in \mathrm {R}^*(\mathfrak {M}_{g,n+1,a})$
under the map
$[\Gamma , \alpha ] \in \mathrm {R}^*(\mathfrak {M}_{g,n+1,a})$
under the map
![]() $\pi $
.
$\pi $
.
Proposition 3.11. Let
![]() $[\Gamma , \alpha ] \in \mathrm {R}^*(\mathfrak {M}_{g,n+1,a})$
with
$[\Gamma , \alpha ] \in \mathrm {R}^*(\mathfrak {M}_{g,n+1,a})$
with
![]() $\alpha = \prod _{v \in V(\Gamma )} \alpha _v$
. Let
$\alpha = \prod _{v \in V(\Gamma )} \alpha _v$
. Let
![]() $v \in V(\Gamma )$
be the vertex incident to
$v \in V(\Gamma )$
be the vertex incident to
![]() $n+1$
, and let
$n+1$
, and let
![]() $\Gamma '$
be the graph obtained from
$\Gamma '$
be the graph obtained from
![]() $\Gamma $
by forgetting the marking
$\Gamma $
by forgetting the marking
![]() $n+1$
and stabilizing if the vertex v becomes unstable. There are two cases:
$n+1$
and stabilizing if the vertex v becomes unstable. There are two cases:
-
○ If the vertex v remains stable, then
where $$\begin{align*}\pi_* [\Gamma,\alpha] = (\xi_{\Gamma'})_*\left((\pi_v)_* \alpha_v \cdot \prod_{w \neq v} \alpha_w \right), \end{align*}$$
$$\begin{align*}\pi_* [\Gamma,\alpha] = (\xi_{\Gamma'})_*\left((\pi_v)_* \alpha_v \cdot \prod_{w \neq v} \alpha_w \right), \end{align*}$$
 $\pi _v$
is the forgetful map of marking
$\pi _v$
is the forgetful map of marking
 $n+1$
of vertex v.
$n+1$
of vertex v.
-
○ If the vertex v becomes unstable, then
 $g(v)=0$
,
$g(v)=0$
,
 $n(v)=3$
and
$n(v)=3$
and
 . If
. If
 $\alpha _v \neq 1$
, then
$\alpha _v \neq 1$
, then
 $[\Gamma , \alpha ]=0$
. Otherwise, we have
$[\Gamma , \alpha ]=0$
. Otherwise, we have  $$\begin{align*}\pi_* [\Gamma,\alpha] = [\Gamma', \prod_{w \neq v} \alpha_w].\end{align*}$$
$$\begin{align*}\pi_* [\Gamma,\alpha] = [\Gamma', \prod_{w \neq v} \alpha_w].\end{align*}$$
Proof. The result follows from the fact that the composition of the gluing map
![]() $\xi _{\Gamma }$
and the forgetful map
$\xi _{\Gamma }$
and the forgetful map
![]() $\pi $
factors through the gluing map
$\pi $
factors through the gluing map
![]() $\xi _{\Gamma '}$
downstairs. In the second part, we use that
$\xi _{\Gamma '}$
downstairs. In the second part, we use that
![]() , so any nontrivial decoration by
, so any nontrivial decoration by
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes on this space vanishes.
$\psi $
-classes on this space vanishes.
The proposition allows us to reduce to computing forgetful pushforwards of products of
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes. As in the case of
$\psi $
-classes. As in the case of
![]() $\overline {\mathcal {M}}_{g,n}$
, these can be computed using the projection formula. Indeed, given a product
$\overline {\mathcal {M}}_{g,n}$
, these can be computed using the projection formula. Indeed, given a product
 $$\begin{align*}\alpha = \prod_{a} \kappa_a^{e_a} \cdot \prod_{i=1}^n \psi_i^{\ell_i} \cdot \psi_{n+1}^{\ell_{n+1}} \in \mathrm{R}^*(\mathfrak{M}_{g,n+1,a}),\end{align*}$$
$$\begin{align*}\alpha = \prod_{a} \kappa_a^{e_a} \cdot \prod_{i=1}^n \psi_i^{\ell_i} \cdot \psi_{n+1}^{\ell_{n+1}} \in \mathrm{R}^*(\mathfrak{M}_{g,n+1,a}),\end{align*}$$
we can use Proposition 3.10 and the known intersection formulas on
![]() $\mathfrak {M}_{g,n+1,a}$
to write it as
$\mathfrak {M}_{g,n+1,a}$
to write it as
 $$\begin{align*}\alpha = \pi^* \left( \prod_{a} \kappa_a^{e_a} \cdot \prod_{i=1}^n \psi_i^{\ell_i}\right)\cdot \psi_{n+1}^{\ell_{n+1}} + \text{boundary terms}. \end{align*}$$
$$\begin{align*}\alpha = \pi^* \left( \prod_{a} \kappa_a^{e_a} \cdot \prod_{i=1}^n \psi_i^{\ell_i}\right)\cdot \psi_{n+1}^{\ell_{n+1}} + \text{boundary terms}. \end{align*}$$
Using the projection formula, we conclude
 $$\begin{align*}\pi_*(\alpha) = \left( \prod_{a} \kappa_a^{e_a} \cdot \prod_{i=1}^n \psi_i^{\ell_i}\right)\cdot \kappa_{\ell_{n+1}-1} + \pi_*(\text{boundary terms}), \end{align*}$$
$$\begin{align*}\pi_*(\alpha) = \left( \prod_{a} \kappa_a^{e_a} \cdot \prod_{i=1}^n \psi_i^{\ell_i}\right)\cdot \kappa_{\ell_{n+1}-1} + \pi_*(\text{boundary terms}), \end{align*}$$
where
![]() $\kappa _0=2g-2+n$
and
$\kappa _0=2g-2+n$
and
![]() $\kappa _{-1}=0$
. The boundary terms are handled by induction on the degree together with Proposition 3.11.
$\kappa _{-1}=0$
. The boundary terms are handled by induction on the degree together with Proposition 3.11.
Together with the previous results of this section, this shows that the
![]() $\mathbb {Q}$
-linear span of the decorated strata classes
$\mathbb {Q}$
-linear span of the decorated strata classes
![]() $[\Gamma , \alpha ]$
in
$[\Gamma , \alpha ]$
in
![]() $\mathrm {CH}^*(\mathfrak {M}_{g,n,a})$
is closed under intersections as well as pushforwards under gluing and forgetful maps. Thus, by definition, it equals the tautological ring of
$\mathrm {CH}^*(\mathfrak {M}_{g,n,a})$
is closed under intersections as well as pushforwards under gluing and forgetful maps. Thus, by definition, it equals the tautological ring of
![]() $\mathfrak {M}_{g,n,a}$
so that we have finished the proof of Theorem 1.4.
$\mathfrak {M}_{g,n,a}$
so that we have finished the proof of Theorem 1.4.
Pullbacks by forgetful maps of
 $\mathcal {A}$
-values
$\mathcal {A}$
-values
Proposition 3.12. For the map
![]() $F_{\mathcal {A}}: \mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n}$
forgetting the
$F_{\mathcal {A}}: \mathfrak {M}_{g,n,a} \to \mathfrak {M}_{g,n}$
forgetting the
![]() $\mathcal {A}$
-values on all components of the curve, without stabilizing, we have
$\mathcal {A}$
-values on all components of the curve, without stabilizing, we have
 $$\begin{align*}F_{\mathcal{A}}^* [\Gamma,\alpha] = \sum_{\substack{(a_v)_{v \in V(\Gamma)}\\\sum_v a_v=a}} [\Gamma_{(a_v)_v}, \alpha],\end{align*}$$
$$\begin{align*}F_{\mathcal{A}}^* [\Gamma,\alpha] = \sum_{\substack{(a_v)_{v \in V(\Gamma)}\\\sum_v a_v=a}} [\Gamma_{(a_v)_v}, \alpha],\end{align*}$$
where the sum is over tuples
![]() $(a_v)_v$
of elements of
$(a_v)_v$
of elements of
![]() $\mathcal {A}$
summing to a, such that the
$\mathcal {A}$
summing to a, such that the
![]() $\mathcal {A}$
-valuation
$\mathcal {A}$
-valuation
![]() $v \mapsto a_v$
on the vertices v of
$v \mapsto a_v$
on the vertices v of
![]() $\Gamma $
gives a well-defined
$\Gamma $
gives a well-defined
![]() $\mathcal {A}$
-valued graph
$\mathcal {A}$
-valued graph
![]() $\Gamma _{(a_v)_v}$
.
$\Gamma _{(a_v)_v}$
.
Proof. The fibre product of
![]() $F_{\mathcal {A}}$
and a gluing map
$F_{\mathcal {A}}$
and a gluing map
![]() $\xi _{\Gamma }$
is the disjoint union of the gluing maps
$\xi _{\Gamma }$
is the disjoint union of the gluing maps
![]() $\xi _{\Gamma _{(a_v)_v}}$
. A short computation shows that
$\xi _{\Gamma _{(a_v)_v}}$
. A short computation shows that
![]() $F_{\mathcal {A}}^* \psi _i = \psi _i$
and
$F_{\mathcal {A}}^* \psi _i = \psi _i$
and
![]() $F_{\mathcal {A}}^* \kappa _a = \kappa _a$
.
$F_{\mathcal {A}}^* \kappa _a = \kappa _a$
.
Pullback by stabilization map
We saw before that the stabilization morphism
![]() $\mathrm {st}: \mathfrak {M}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
is flat, so we can ask how to pull back tautological classes along this morphism. We start by computing the pullback of gluing maps under
$\mathrm {st}: \mathfrak {M}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
is flat, so we can ask how to pull back tautological classes along this morphism. We start by computing the pullback of gluing maps under
![]() $\mathrm {st}$
.
$\mathrm {st}$
.
Proposition 3.13. Given a stable graph
![]() $\Gamma $
in genus g with n marked points (for
$\Gamma $
in genus g with n marked points (for
![]() $2g-2+n>0$
), we have a commutative diagram
$2g-2+n>0$
), we have a commutative diagram

where
![]() $\mathrm {st}_v : \mathfrak {M}_{g(v),n(v)} \to \overline {\mathcal {M}}_{g(v),n(v)}$
is the stabilization morphism at vertex v. Moreover, the induced map
$\mathrm {st}_v : \mathfrak {M}_{g(v),n(v)} \to \overline {\mathcal {M}}_{g(v),n(v)}$
is the stabilization morphism at vertex v. Moreover, the induced map
is proper and birational. In particular
 $$ \begin{align} \mathrm{st}^* \left[\Gamma, \prod_v \alpha_v\right] = (\xi_{\Gamma})_* \left( \prod_v {\mathrm{st}_v^*} \alpha_v \right). \end{align} $$
$$ \begin{align} \mathrm{st}^* \left[\Gamma, \prod_v \alpha_v\right] = (\xi_{\Gamma})_* \left( \prod_v {\mathrm{st}_v^*} \alpha_v \right). \end{align} $$
Proof. The commutativity of the diagram in equation (23) follows from the definition of the stabilization. The map in equation (24) is easily seen to be birational, and its properness follows from the diagram

and the cancellation property of proper morphisms (in the diagram, the map
![]() $\xi _{\Gamma }$
and
$\xi _{\Gamma }$
and
![]() $\mathrm {pr}_1$
are proper). Equation (25) again follows by an application of Lemma C.8.
$\mathrm {pr}_1$
are proper). Equation (25) again follows by an application of Lemma C.8.
The proposition above reduces the pullback of tautological classes under
![]() $\mathrm {st}$
to computing the pullback of
$\mathrm {st}$
to computing the pullback of
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes.
$\psi $
-classes.
Proposition 3.14. Let
![]() $g,n$
with
$g,n$
with
![]() $2g-2+n>0$
, and let
$2g-2+n>0$
, and let
![]() . Then for
. Then for
![]() $1 \leq i \leq n$
and the stabilization map
$1 \leq i \leq n$
and the stabilization map
![]() , we have
, we have

Proof. Consider the commutative diagram

where the right square is Cartesian and the map c is the map contracting the unstable components of the universal curve
![]() . By the cancellation property of proper morphisms, the map c is proper and easily seen to be birational.
. By the cancellation property of proper morphisms, the map c is proper and easily seen to be birational.
For computing the pullback of
![]() $\psi _i$
under
$\psi _i$
under
![]() $\mathrm {st}_{\mathcal {A}}$
, we use that
$\mathrm {st}_{\mathcal {A}}$
, we use that
![]() $\psi _i = -\pi _*( D_{i,n+1}^2)$
on
$\psi _i = -\pi _*( D_{i,n+1}^2)$
on
![]() $\overline {\mathcal {M}}_{g,n}$
, where
$\overline {\mathcal {M}}_{g,n}$
, where
![]() $D_{i,n+1} \subset \overline {\mathcal {M}}_{g,n+1}$
is the image of the ith section. By Lemma C.8, we have
$D_{i,n+1} \subset \overline {\mathcal {M}}_{g,n+1}$
is the image of the ith section. By Lemma C.8, we have
The composition
![]() $c \circ \widehat {\mathrm {st}}_{\mathcal {A}}$
is just the usual stabilization map, and the pullback of
$c \circ \widehat {\mathrm {st}}_{\mathcal {A}}$
is just the usual stabilization map, and the pullback of
![]() $D_{i,n+1}$
under this map is the sum of three boundary divisors of
$D_{i,n+1}$
under this map is the sum of three boundary divisors of
![]() : their underlying graph is the same as for
: their underlying graph is the same as for
![]() $D_{i,n+1}$
and the
$D_{i,n+1}$
and the
![]() $\mathcal {A}$
-values correspond to the three different ways
$\mathcal {A}$
-values correspond to the three different ways
![]() to distribute the value
to distribute the value
![]() to the two vertices. A short computation using the rules for intersection and pushforward presented earlier gives the formula in equation (26).
to the two vertices. A short computation using the rules for intersection and pushforward presented earlier gives the formula in equation (26).
The formula for the pullback of
![]() $\kappa $
-classes is more involved, and we need to introduce a bit of notation to state it. Fix
$\kappa $
-classes is more involved, and we need to introduce a bit of notation to state it. Fix
![]() $g,n$
with
$g,n$
with
![]() $2g-2+n>0$
; then for
$2g-2+n>0$
; then for
![]() $k \geq 0$
, let
$k \geq 0$
, let
![]() $\widehat G_k, G_k$
be the following
$\widehat G_k, G_k$
be the following
![]() $(n+1)$
and n-pointed prestable graphs in genus g with k edges
$(n+1)$
and n-pointed prestable graphs in genus g with k edges

Here
![]() $v_0$
is the leftmost vertex and, for
$v_0$
is the leftmost vertex and, for
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $h_0$
is the unique half-edge incident to this vertex. For
$h_0$
is the unique half-edge incident to this vertex. For
![]() $k=0$
, the graphs
$k=0$
, the graphs
![]() $\widehat {G}_k, G_k$
are the trivial graphs, respectively.
$\widehat {G}_k, G_k$
are the trivial graphs, respectively.
Also, in the proposition below, we consider the power series
We use the notation
![]() $[\Phi (t)]_{t^a \mapsto \kappa _a}$
to indicate that in the power series
$[\Phi (t)]_{t^a \mapsto \kappa _a}$
to indicate that in the power series
![]() $\Phi $
, the term
$\Phi $
, the term
![]() $t^a$
is substituted with the class
$t^a$
is substituted with the class
![]() $\kappa _a$
, getting the mixed-degree Chow class
$\kappa _a$
, getting the mixed-degree Chow class
Proposition 3.15. For
![]() $g,n$
with
$g,n$
with
![]() $2g-2+n>0$
, the stabilization morphism
$2g-2+n>0$
, the stabilization morphism
![]() $\mathrm {st}: \mathfrak {M}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
satisfies the following equality of mixed-degree Chow classes on
$\mathrm {st}: \mathfrak {M}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
satisfies the following equality of mixed-degree Chow classes on
![]() $\mathfrak {M}_{g,n}$
:
$\mathfrak {M}_{g,n}$
:
 $$ \begin{align} &\mathrm{st}^*\left[\Phi(t)\right]_{t^a \mapsto \kappa_a} \nonumber \\=& \left[\Phi(t)\right]_{t^a \mapsto \kappa_a} + \sum_{k \geq 1} (\xi_{G_k})_* \left( \left(\left[\Phi(t) \right]_{t^a \mapsto \kappa_{v_0,a}} + \psi_{h_0}^{-1} \right) \cdot \mathrm{Cont}_{E(G_k)} \right). \end{align} $$
$$ \begin{align} &\mathrm{st}^*\left[\Phi(t)\right]_{t^a \mapsto \kappa_a} \nonumber \\=& \left[\Phi(t)\right]_{t^a \mapsto \kappa_a} + \sum_{k \geq 1} (\xi_{G_k})_* \left( \left(\left[\Phi(t) \right]_{t^a \mapsto \kappa_{v_0,a}} + \psi_{h_0}^{-1} \right) \cdot \mathrm{Cont}_{E(G_k)} \right). \end{align} $$
Here
![]() $\mathrm {Cont}_{E(G_k)}$
is the mixed-degree class
$\mathrm {Cont}_{E(G_k)}$
is the mixed-degree class
on
![]() $\mathfrak {M}_{G_k}$
. In the formula above, the term
$\mathfrak {M}_{G_k}$
. In the formula above, the term
![]() $\psi _{h_0}^{-1}$
is understood to vanish unless it pairs with a term of
$\psi _{h_0}^{-1}$
is understood to vanish unless it pairs with a term of
![]() $\mathrm {Cont}_{E(G_k)}$
containing a positive power of
$\mathrm {Cont}_{E(G_k)}$
containing a positive power of
![]() $\psi _{h_0}$
, and we have
$\psi _{h_0}$
, and we have
![]() $\kappa _{v_0,0}=2\cdot 0 -2+1=-1$
.
$\kappa _{v_0,0}=2\cdot 0 -2+1=-1$
.
To obtain the pullback of an individual class
![]() $\kappa _a$
under
$\kappa _a$
under
![]() $\mathrm {st}$
, we take the degree a part of equation (28) and obtain a formula of the form
$\mathrm {st}$
, we take the degree a part of equation (28) and obtain a formula of the form
As an example, for
![]() $a=1,2$
, we obtain
$a=1,2$
, we obtain
and
where
![]() $e=(h_0,h_1)$
is the unique edge of the graph
$e=(h_0,h_1)$
is the unique edge of the graph
![]() $G_1$
.
$G_1$
.
Proof of Proposition 3.15
Consider the following commutative diagram:

Then as
![]() $\mathfrak {C}_{g,n}$
maps proper and birationally to the fibre product in the right diagram, we have
$\mathfrak {C}_{g,n}$
maps proper and birationally to the fibre product in the right diagram, we have
Here we use that computations in
![]() $\mathfrak {C}_{g,n}$
can be performed in
$\mathfrak {C}_{g,n}$
can be performed in
![]() together with the pullback formula from Proposition 3.14 (noting that the third term in in equation (26) vanishes since it lies in the complement of the open substack
together with the pullback formula from Proposition 3.14 (noting that the third term in in equation (26) vanishes since it lies in the complement of the open substack
![]()
From now on, it will be more convenient working with mixed-degree classes and exponentials. In this language, equation (30) translates to
The occurrence of the power series
![]() $\Phi $
is due to the discrepancy between the degree a of
$\Phi $
is due to the discrepancy between the degree a of
![]() $\kappa _a$
on the left of equation (30) and the degree
$\kappa _a$
on the left of equation (30) and the degree
![]() $a+1$
of the term on the right. Using the rules for intersections of tautological classes, one shows
$a+1$
of the term on the right. Using the rules for intersections of tautological classes, one shows
 $$ \begin{align} \exp(- [\widehat{G}_1]) = \sum_{k\geq 1} (\xi_{\widehat{G}_k})_* \left( \prod_{(h,h') \in E(\widehat{G}_k)} - \Phi(\psi_h + \psi_{h'}) \right). \end{align} $$
$$ \begin{align} \exp(- [\widehat{G}_1]) = \sum_{k\geq 1} (\xi_{\widehat{G}_k})_* \left( \prod_{(h,h') \in E(\widehat{G}_k)} - \Phi(\psi_h + \psi_{h'}) \right). \end{align} $$
Now, in the pushforward in equation (31), the only terms supported on the trivial graph are those from
explaining the first term of the answer. All other terms of the product of the exponentials are supported on some
![]() $\widehat {G}_k$
for
$\widehat {G}_k$
for
![]() $k \geq 1$
, where marking
$k \geq 1$
, where marking
![]() $n+1$
is on a rational component with just one other half-edge
$n+1$
is on a rational component with just one other half-edge
![]() $h_0$
. Using the formulas for the pushforward by the forgetful map
$h_0$
. Using the formulas for the pushforward by the forgetful map
![]() $\pi '$
from Proposition 3.11, the only nontrivial pushforward we have to compute is the one by the universal curve
$\pi '$
from Proposition 3.11, the only nontrivial pushforward we have to compute is the one by the universal curve
![]() $\pi _{0,1}: \mathfrak {C}_{0,1} \to \mathfrak {M}_{0,1}$
, corresponding to forgetting
$\pi _{0,1}: \mathfrak {C}_{0,1} \to \mathfrak {M}_{0,1}$
, corresponding to forgetting
![]() $n+1$
on the
$n+1$
on the
![]() $2$
-marked genus
$2$
-marked genus
![]() $0$
component
$0$
component
![]() $v_0$
of
$v_0$
of
![]() $\widehat {G}_k$
. Here, a short computation shows
$\widehat {G}_k$
. Here, a short computation shows
where
![]() $\delta _{a,0}$
is the Kronecker delta, and we have the convention
$\delta _{a,0}$
is the Kronecker delta, and we have the convention
![]() $\kappa _{-1}=\psi _1^{-1}=0$
. Applying this formula for the pushforward, the first term in equation (33) gives rise to the term of the result involving
$\kappa _{-1}=\psi _1^{-1}=0$
. Applying this formula for the pushforward, the first term in equation (33) gives rise to the term of the result involving
![]() $\left [\Phi (t) \right ]_{t^a \mapsto \kappa _{v_0,a}}$
, where again
$\left [\Phi (t) \right ]_{t^a \mapsto \kappa _{v_0,a}}$
, where again
![]() $\Phi $
appears due to the shift of degree from b to
$\Phi $
appears due to the shift of degree from b to
![]() $b-1$
in equation (33). The second term of equation (33) gives rise to the term involving
$b-1$
in equation (33). The second term of equation (33) gives rise to the term involving
![]() $\psi _{h_0}^{-1}$
, where due to the Kronecker delta
$\psi _{h_0}^{-1}$
, where due to the Kronecker delta
![]() $\delta _{a,0}$
only the constant term of
$\delta _{a,0}$
only the constant term of
![]() $\exp (\psi _{n+1})$
survives in the pushforward.
$\exp (\psi _{n+1})$
survives in the pushforward.
Remark 3.16. The following is a nontrivial check and application of the computations from the last sections: for
![]() $g,n,m$
with
$g,n,m$
with
![]() $2g-2+n>0$
, consider the diagram
$2g-2+n>0$
, consider the diagram

where
![]() $F_m$
is the map forgetting the last m markings (without stabilizing the curve), the map
$F_m$
is the map forgetting the last m markings (without stabilizing the curve), the map
![]() $\mathrm {st}$
is the stabilization map and their composition
$\mathrm {st}$
is the stabilization map and their composition
![]() $\pi $
is the ‘usual’ forgetful map between moduli spaces of stable curves. The pullback of tautological classes under
$\pi $
is the ‘usual’ forgetful map between moduli spaces of stable curves. The pullback of tautological classes under
![]() $\pi $
is known classically, and the pullback by the two other maps has been computed in the previous sections. Since the pullbacks must be compatible, this gives rise to tautological relations, which we can verify in examples.
$\pi $
is known classically, and the pullback by the two other maps has been computed in the previous sections. Since the pullbacks must be compatible, this gives rise to tautological relations, which we can verify in examples.
For instance, for the class
![]() $\kappa _1 \in \mathrm {CH}^1(\overline {\mathcal {M}}_{g,n})$
, we have
$\kappa _1 \in \mathrm {CH}^1(\overline {\mathcal {M}}_{g,n})$
, we have
 $$\begin{align*}\pi^* \kappa_1 = \kappa_1 - \sum_{i=n+1}^{n+m} \psi_i + \sum_{\substack{I \subset \{n+1, \ldots, n+m\}\\|I| \geq 2}} D_{0,I},\end{align*}$$
$$\begin{align*}\pi^* \kappa_1 = \kappa_1 - \sum_{i=n+1}^{n+m} \psi_i + \sum_{\substack{I \subset \{n+1, \ldots, n+m\}\\|I| \geq 2}} D_{0,I},\end{align*}$$
where
![]() $D_{0,I} \subset \overline {\mathcal {M}}_{g,n+m}$
is the boundary divisor of curves with a rational component carrying markings I. On the other hand we have
$D_{0,I} \subset \overline {\mathcal {M}}_{g,n+m}$
is the boundary divisor of curves with a rational component carrying markings I. On the other hand we have
 $$ \begin{align*} \mathrm{st}^* \kappa_1 &= \kappa_1 + [G_1] = \kappa_1 + D_{0,\emptyset}\\ \pi^* \mathrm{st}^* \kappa_1 &= \kappa_1 - \sum_{i=n+1}^{n+m} \psi_i + \sum_{\substack{I \subset \{n+1, \ldots, n+m\}\\|I| \geq 2}} D_{0,I}. \end{align*} $$
$$ \begin{align*} \mathrm{st}^* \kappa_1 &= \kappa_1 + [G_1] = \kappa_1 + D_{0,\emptyset}\\ \pi^* \mathrm{st}^* \kappa_1 &= \kappa_1 - \sum_{i=n+1}^{n+m} \psi_i + \sum_{\substack{I \subset \{n+1, \ldots, n+m\}\\|I| \geq 2}} D_{0,I}. \end{align*} $$
So indeed we get the same answer.
4 Relation to previous works
In this section, we review several results in the literature relating to our study of the intersection theory of the stacks
![]() $\mathfrak {M}_{g,n}$
.
$\mathfrak {M}_{g,n}$
.
Example 4.1. In [Reference GathmannGat03, Lemma 1], Gathmann used the pullback formula of
![]() $\psi $
-classes along the stabilization morphism
$\psi $
-classes along the stabilization morphism
![]() $\mathrm {st}\colon \mathfrak {M}_{g,1}\to \overline {\mathcal {M}}_{g,1}$
to prove certain properties of the Gromov–Witten potential. It coincides with our calculation in Proposition 3.14.
$\mathrm {st}\colon \mathfrak {M}_{g,1}\to \overline {\mathcal {M}}_{g,1}$
to prove certain properties of the Gromov–Witten potential. It coincides with our calculation in Proposition 3.14.
Example 4.2. In [Reference PixtonPix18], Pixton introduces classes
![]() $[\Gamma ] \in \mathrm {R}^*(\overline {\mathcal {M}}_{g,n})$
indexed by prestable graphs of genus g with n legs. In his construction, chains of unstable vertices encode insertions of
$[\Gamma ] \in \mathrm {R}^*(\overline {\mathcal {M}}_{g,n})$
indexed by prestable graphs of genus g with n legs. In his construction, chains of unstable vertices encode insertions of
![]() $\kappa $
and
$\kappa $
and
![]() $\psi $
-classes in such a way that the formula for products
$\psi $
-classes in such a way that the formula for products
![]() $[\Gamma ] \cdot [\Gamma ']$
takes a particularly simple shape. While it is not a priori obvious how to relate his classes to the corresponding boundary strata classes
$[\Gamma ] \cdot [\Gamma ']$
takes a particularly simple shape. While it is not a priori obvious how to relate his classes to the corresponding boundary strata classes
![]() $[\Gamma ] \in \mathrm {R}^*(\mathfrak {M}_{g,n})$
in the moduli stack of prestable curves, this is a question we plan to investigate in future work.
$[\Gamma ] \in \mathrm {R}^*(\mathfrak {M}_{g,n})$
in the moduli stack of prestable curves, this is a question we plan to investigate in future work.
Example 4.3. In [Reference OesinghausOes19], Oesinghaus computes the Chow ring (with integral coefficients) of a certain open substack
![]() $\mathcal {T}$
of
$\mathcal {T}$
of
![]() $\mathfrak {M}_{0,3}$
, defined by the conditions that the curve is semistable (i.e., every component of the curve has at least two distinguished points) and that the markings
$\mathfrak {M}_{0,3}$
, defined by the conditions that the curve is semistable (i.e., every component of the curve has at least two distinguished points) and that the markings
![]() $2,3$
are on a stable component of the curve. As a consequence, the prestable graphs of geometric points of
$2,3$
are on a stable component of the curve. As a consequence, the prestable graphs of geometric points of
![]() $\mathcal {T}$
are all of the form
$\mathcal {T}$
are all of the form

where we denote by
![]() $\Gamma _k$
the graph of the shape above with k edges (for
$\Gamma _k$
the graph of the shape above with k edges (for
![]() $k \geq 0$
). The stack
$k \geq 0$
). The stack
![]() $\mathcal {T} $
has an atlas given by
$\mathcal {T} $
has an atlas given by
Since
![]() $\mathcal {A}^n$
is a vector bundle over
$\mathcal {A}^n$
is a vector bundle over
![]() $B \mathbb {G}_m^n$
, its Chow groupFootnote
14
is given by
$B \mathbb {G}_m^n$
, its Chow groupFootnote
14
is given by
where
![]() $\alpha _{\ell }$
is the class of the
$\alpha _{\ell }$
is the class of the
![]() $\ell $
th coordinate hyperplane
$\ell $
th coordinate hyperplane
From a computation in [Reference OesinghausOes19, Lemma 1], it follows that the first Chern class of the normal bundle of
![]() $\iota _{\ell }$
is given by the restriction
$\iota _{\ell }$
is given by the restriction
of
![]() $\alpha _{\ell }$
to this hyperplane. Using the charts
$\alpha _{\ell }$
to this hyperplane. Using the charts
![]() $\pi _n$
, Oesinghaus shows that the Chow ring
$\pi _n$
, Oesinghaus shows that the Chow ring
![]() $\mathrm {CH}^*(\mathcal {T}\;)$
is given by the ring QSym of quasi-symmetric functions on the index set
$\mathrm {CH}^*(\mathcal {T}\;)$
is given by the ring QSym of quasi-symmetric functions on the index set
![]() $\mathbb {Z}_{>0}$
. QSym can be seen as the subring of
$\mathbb {Z}_{>0}$
. QSym can be seen as the subring of
![]() $\mathbb {Q}[\alpha _1, \alpha _2, \ldots ]$
with additive basis given by
$\mathbb {Q}[\alpha _1, \alpha _2, \ldots ]$
with additive basis given by
Under the isomorphism
![]() $\mathrm {CH}^*(\mathcal {T}\;) \cong \text {QSym}$
, the element
$\mathrm {CH}^*(\mathcal {T}\;) \cong \text {QSym}$
, the element
![]() $M_J$
is a basis element of degree
$M_J$
is a basis element of degree
![]() $\sum _{\ell } j_{\ell }$
in the Chow group of
$\sum _{\ell } j_{\ell }$
in the Chow group of
![]() $\mathcal {T}$
. The pullback
$\mathcal {T}$
. The pullback
is induced by the map sending
![]() $\alpha _m$
to zero for
$\alpha _m$
to zero for
![]() $m> n$
. In particular, it is easy to see that it is injective in Chow-degree at most n.
$m> n$
. In particular, it is easy to see that it is injective in Chow-degree at most n.
With these preparations in place, we can now identify the generators
![]() $M_J$
of
$M_J$
of
![]() $\mathrm {CH}^*(\mathcal {T})$
with tautological classes. Indeed, we claim that
$\mathrm {CH}^*(\mathcal {T})$
with tautological classes. Indeed, we claim that
![]() $M_J$
corresponds to the class supported on the stratum
$M_J$
corresponds to the class supported on the stratum
![]() $\mathfrak {M}^{\Gamma _k}$
given by
$\mathfrak {M}^{\Gamma _k}$
given by

To see this, we note that from the definition of the charts
![]() $\pi _n$
in [Reference OesinghausOes19, Section 3.3] one can show that we have a fibre diagram
$\pi _n$
in [Reference OesinghausOes19, Section 3.3] one can show that we have a fibre diagram

As a first example, this implies that
![]() $[\Gamma _k,1] = (\xi _{\Gamma _k})_* [\mathfrak {M}_{\Gamma _k}]$
corresponds to the class
$[\Gamma _k,1] = (\xi _{\Gamma _k})_* [\mathfrak {M}_{\Gamma _k}]$
corresponds to the class
on
![]() $\mathcal {A}^n$
, which indeed is equal to
$\mathcal {A}^n$
, which indeed is equal to
![]() $\pi _n^*(M_{(1, \ldots , 1)})$
. For the comparison of more complicated classes, we observe that the decorations
$\pi _n^*(M_{(1, \ldots , 1)})$
. For the comparison of more complicated classes, we observe that the decorations
![]() $(-\psi - \psi ')^{j_{\ell }-1}$
are the
$(-\psi - \psi ')^{j_{\ell }-1}$
are the
![]() $(j_{\ell }-1)$
-st powers of the Chern class of the normal bundle associated to the
$(j_{\ell }-1)$
-st powers of the Chern class of the normal bundle associated to the
![]() $\ell $
th edge of
$\ell $
th edge of
![]() $\Gamma _k$
. On the other hand, in the diagram in equation (37), the function
$\Gamma _k$
. On the other hand, in the diagram in equation (37), the function
![]() $x_{i_{\ell }}$
around the linear subspace
$x_{i_{\ell }}$
around the linear subspace
![]() $V(x_{i_1}, \ldots , x_{i_k})$
is the smoothing parameter for the
$V(x_{i_1}, \ldots , x_{i_k})$
is the smoothing parameter for the
![]() $\ell $
th node of the curve and the first Chern class of the normal bundle to the locus
$\ell $
th node of the curve and the first Chern class of the normal bundle to the locus
![]() $V(x_{i_{\ell }})$
, and where the
$V(x_{i_{\ell }})$
, and where the
![]() $\ell $
th node persists is given by (the restriction of)
$\ell $
th node persists is given by (the restriction of)
![]() $\alpha _{i_{\ell }}$
. Since
$\alpha _{i_{\ell }}$
. Since
![]() $V(x_{i_1}, \ldots , x_{i_k})$
has class
$V(x_{i_1}, \ldots , x_{i_k})$
has class
![]() $\alpha _{i_1} \cdots \alpha _{i_k}$
in
$\alpha _{i_1} \cdots \alpha _{i_k}$
in
![]() $\mathcal {A}_n$
, we conclude that the element equation (36) of
$\mathcal {A}_n$
, we conclude that the element equation (36) of
![]() $\mathrm {CH}^*(\mathcal {T})$
pulls back via
$\mathrm {CH}^*(\mathcal {T})$
pulls back via
![]() $\pi _n$
to
$\pi _n$
to
This shows the desired correspondence because this holds for all n and
![]() $\pi _n^*$
is injective in degree at most n.
$\pi _n^*$
is injective in degree at most n.
Using the correspondence, it is straightforward to see that the product formula for expressing
![]() $M_J \cdot M_{J'}$
in terms of basis elements
$M_J \cdot M_{J'}$
in terms of basis elements
![]() $M_{J_i}$
discussed in [Reference OesinghausOes19, Proposition 2] follows from the product formula for decorated strata classes discussed in Section 3.2.
$M_{J_i}$
discussed in [Reference OesinghausOes19, Proposition 2] follows from the product formula for decorated strata classes discussed in Section 3.2.
In [Reference OesinghausOes19], Oesinghaus also computes the Chow group of the semistable loci
![]() $\mathfrak {M}_{0,2}^{ss}$
and
$\mathfrak {M}_{0,2}^{ss}$
and
![]() $\mathfrak {M}_{0,3}^{ss}$
, and there are correspondence results to the tautological generators of these spaces closely parallel to the above discussion. We leave the details to the interested reader.
$\mathfrak {M}_{0,3}^{ss}$
, and there are correspondence results to the tautological generators of these spaces closely parallel to the above discussion. We leave the details to the interested reader.
A Chow groups of locally finite type algebraic stacks
The Chow group of a finite type algebraic stack over a field k is defined in [Reference KreschKre99]. We extend this notion to an algebraic stack that is not necessarily of finite type over k.
Definition A.1. Let
![]() $\mathfrak {M}$
be an algebraic stack, locally of finite type over a field k. Choose
$\mathfrak {M}$
be an algebraic stack, locally of finite type over a field k. Choose
![]() $(\mathcal {U}_i)_{i \in I}$
a directed systemFootnote
15
of finite type open substacks of
$(\mathcal {U}_i)_{i \in I}$
a directed systemFootnote
15
of finite type open substacks of
![]() $\mathfrak {M}$
whose union is all of
$\mathfrak {M}$
whose union is all of
![]() $\mathfrak {M}$
. Then we define
$\mathfrak {M}$
. Then we define
where for
![]() $\mathcal U_i \subseteq \mathcal U_j$
, the transition map
$\mathcal U_i \subseteq \mathcal U_j$
, the transition map
![]() $\mathrm {CH}_*(\mathcal U_j) \to \mathrm {CH}_*(\mathcal U_i)$
is given by the restriction to
$\mathrm {CH}_*(\mathcal U_j) \to \mathrm {CH}_*(\mathcal U_i)$
is given by the restriction to
![]() $\mathcal U_i$
. In other words, we have
$\mathcal U_i$
. In other words, we have
For the existence of a system
![]() $(\mathcal {U}_i)_{i \in I}$
as above, observe that since
$(\mathcal {U}_i)_{i \in I}$
as above, observe that since
![]() $\mathfrak {M}$
is locally of finite type, we can simply take the system of all finite type substacks
$\mathfrak {M}$
is locally of finite type, we can simply take the system of all finite type substacks
![]() $\mathcal U \subset \mathfrak {M}$
. Moreover, given any two systems
$\mathcal U \subset \mathfrak {M}$
. Moreover, given any two systems
![]() $(\mathcal {U}_i)_{i \in I}$
,
$(\mathcal {U}_i)_{i \in I}$
,
![]() $(\mathcal {U}^{\prime }_i)_{i \in I'}$
, one uses Noetherian induction to show that they mutually dominate each other. By standard arguments, the Chow group
$(\mathcal {U}^{\prime }_i)_{i \in I'}$
, one uses Noetherian induction to show that they mutually dominate each other. By standard arguments, the Chow group
![]() $\mathrm {CH}_*(\mathfrak {M})$
is independent of the choice of
$\mathrm {CH}_*(\mathfrak {M})$
is independent of the choice of
![]() $(\mathcal {U}_i)_{i \in I}$
.
$(\mathcal {U}_i)_{i \in I}$
.
From the definition as a limit, one sees that the Chow groups
![]() $\mathrm {CH}_*(\mathfrak {M})$
inherit all the usual properties (e.g., flat pullback, projective pushforward, Chern classes of vector bundles and Gysin pullbacks) of the Chow groups from [Reference KreschKre99]. Moreover, if
$\mathrm {CH}_*(\mathfrak {M})$
inherit all the usual properties (e.g., flat pullback, projective pushforward, Chern classes of vector bundles and Gysin pullbacks) of the Chow groups from [Reference KreschKre99]. Moreover, if
![]() $\mathfrak {M}$
is smooth and has affine stabilizer groups at geometric points, the intersection products on the groups
$\mathfrak {M}$
is smooth and has affine stabilizer groups at geometric points, the intersection products on the groups
![]() $\mathrm {CH}_*(\mathcal U_i)$
give rise to an intersection product on
$\mathrm {CH}_*(\mathcal U_i)$
give rise to an intersection product on
![]() $\mathrm {CH}_*(\mathfrak {M})$
. In this case, if
$\mathrm {CH}_*(\mathfrak {M})$
. In this case, if
![]() $\mathfrak {M}$
is equidimensional, we often use the cohomological degree convention
$\mathfrak {M}$
is equidimensional, we often use the cohomological degree convention
The Chow group of a locally finite type algebraic stack is defined as taking a projective limit. Since taking projective limits is not an exact functor and does not commute with tensor products, some of the properties of Chow groups of finite type algebraic stacks do not (obviously) extend. In the following definition, we present two finiteness assumptions on locally finite type stacks, which guarantee that the Chow groups we define continue to have some nice properties (like having an excision sequence).
Definition A.2. Let
![]() $\mathfrak {M}$
be an equidimensional algebraic stack, locally finite type over a field k.
$\mathfrak {M}$
be an equidimensional algebraic stack, locally finite type over a field k.
-
a) We say
 $\mathfrak {M}$
is Lindelöf if every cover of
$\mathfrak {M}$
is Lindelöf if every cover of
 $\mathfrak {M}$
by open substacks has a countable subcover.
$\mathfrak {M}$
by open substacks has a countable subcover. -
b) We say that
 $\mathfrak {M}$
has a good filtration by finite type substacks
Footnote
16
if there exists a collection
$\mathfrak {M}$
has a good filtration by finite type substacks
Footnote
16
if there exists a collection
 $(\mathcal {U}_m)_{m \in \mathbb {N}}$
of open substack of finite type on
$(\mathcal {U}_m)_{m \in \mathbb {N}}$
of open substack of finite type on
 $\mathfrak {M}$
that is increasing (i.e.,
$\mathfrak {M}$
that is increasing (i.e.,
 $\mathcal {U}_m \subset \mathcal {U}_{\ell }$
for
$\mathcal {U}_m \subset \mathcal {U}_{\ell }$
for
 $m<\ell $
) and such that
$m<\ell $
) and such that
 $\mathrm {dim}(\mathfrak {M} \setminus \mathcal {U}_m) < \mathrm {dim}\, \mathfrak {M} -m$
.
$\mathrm {dim}(\mathfrak {M} \setminus \mathcal {U}_m) < \mathrm {dim}\, \mathfrak {M} -m$
.
Lemma A.3. A locally finite type algebraic stack
![]() $\mathfrak {M}$
over k is Lindelöf if and only if it has a countable cover
$\mathfrak {M}$
over k is Lindelöf if and only if it has a countable cover
![]() $(\mathcal {U}_i)_{i\in \mathbb {N}}$
by finite type open substacks
$(\mathcal {U}_i)_{i\in \mathbb {N}}$
by finite type open substacks
![]() $\mathcal {U}_i \subseteq \mathfrak {M}$
. In this case, the cover
$\mathcal {U}_i \subseteq \mathfrak {M}$
. In this case, the cover
![]() $\mathcal {U}_i$
can be chosen to be increasing. In particular, if
$\mathcal {U}_i$
can be chosen to be increasing. In particular, if
![]() $\mathfrak {M}$
has a good filtration by finite type substacks, it is automatically Lindelöf.
$\mathfrak {M}$
has a good filtration by finite type substacks, it is automatically Lindelöf.
Proof. If
![]() $\mathfrak {M}$
is Lindelöf, its cover by the system of all finite type substacks has a countable subcover. Conversely, assume that
$\mathfrak {M}$
is Lindelöf, its cover by the system of all finite type substacks has a countable subcover. Conversely, assume that
![]() $(\mathcal {U}_i)_{i \in \mathbb {N}}$
is a countable cover of
$(\mathcal {U}_i)_{i \in \mathbb {N}}$
is a countable cover of
![]() $\mathfrak {M}$
by finite type open substacks. Given any open cover
$\mathfrak {M}$
by finite type open substacks. Given any open cover
![]() $(\mathcal V_j)_{j \in J}$
of
$(\mathcal V_j)_{j \in J}$
of
![]() $\mathfrak {M}$
, each single open
$\mathfrak {M}$
, each single open
![]() $\mathcal {U}_i$
is covered by finitely many elements
$\mathcal {U}_i$
is covered by finitely many elements
![]() $\mathcal V_{j_{i,\ell }}$
of the second cover via Noetherian induction. Then the system
$\mathcal V_{j_{i,\ell }}$
of the second cover via Noetherian induction. Then the system
![]() $(\mathcal V_{j_{i,\ell }})_{i,\ell }$
is a countable subcover.
$(\mathcal V_{j_{i,\ell }})_{i,\ell }$
is a countable subcover.
Example A.4.
-
a) The stacks
 $\mathfrak {M}_{g,n}$
filtration by finite type substacks, given by the loci
$\mathfrak {M}_{g,n}$
filtration by finite type substacks, given by the loci
 $\mathfrak {M}_{g,n}^{\leq e}$
of curves having at most e nodes.
$\mathfrak {M}_{g,n}^{\leq e}$
of curves having at most e nodes. -
b) The universal Picard stack
 $\mathfrak {Pic}_{g,n}$
over
$\mathfrak {Pic}_{g,n}$
over
 $\mathfrak {M}_{g,n}$
parameterizing tuples of a prestable marked curve and a line bundle
$\mathfrak {M}_{g,n}$
parameterizing tuples of a prestable marked curve and a line bundle $$ \begin{align*}(C,p_1, \ldots, p_n, \mathcal{L})\end{align*} $$
$$ \begin{align*}(C,p_1, \ldots, p_n, \mathcal{L})\end{align*} $$
 $\mathcal {L}$
on C is Lindelöf but does not have a good filtration by finite type substacks.
$\mathcal {L}$
on C is Lindelöf but does not have a good filtration by finite type substacks.
Indeed, we do get a countable cover
 $(\mathcal {U}_m)_{m \in \mathbb {N}}$
by finite type substacks, where
$(\mathcal {U}_m)_{m \in \mathbb {N}}$
by finite type substacks, where
 $\mathcal {U}_m$
is the set of
$\mathcal {U}_m$
is the set of
 $(C,p_1, \ldots , p_n, \mathcal {L})$
such that C has at most m nodes and such that the absolute value of the degree of
$(C,p_1, \ldots , p_n, \mathcal {L})$
such that C has at most m nodes and such that the absolute value of the degree of
 $\mathcal {L}$
on any component of C is at most m. This cover is increasing but does not satisfy that
$\mathcal {L}$
on any component of C is at most m. This cover is increasing but does not satisfy that
 $\dim (\mathfrak {Pic}_{g,n} \setminus \mathcal {U}_m)$
goes to
$\dim (\mathfrak {Pic}_{g,n} \setminus \mathcal {U}_m)$
goes to
 $-\infty $
.
$-\infty $
.The fact that no good filtration can exist follows from the observation that
 $\mathfrak {Pic}_{g,n}$
has infinitely many boundary divisors (corresponding to ways that the degree of
$\mathfrak {Pic}_{g,n}$
has infinitely many boundary divisors (corresponding to ways that the degree of
 $\mathcal {L}$
can split up on the components of a curve with two components) and no finite type stack
$\mathcal {L}$
can split up on the components of a curve with two components) and no finite type stack
 $\mathcal {U}_1$
can contain all generic points of these divisors.
$\mathcal {U}_1$
can contain all generic points of these divisors.The paper [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20] studied cycles and relations in the operational Chow ring
 $\mathrm {CH}^*_{\text {op}}(\mathfrak {Pic}_{g,n})$
; see Section C for details. While we do not pursue this direction of study in the current paper, the Picard stack is one of our main motivations for introducing the property of being Lindelöf.
$\mathrm {CH}^*_{\text {op}}(\mathfrak {Pic}_{g,n})$
; see Section C for details. While we do not pursue this direction of study in the current paper, the Picard stack is one of our main motivations for introducing the property of being Lindelöf. -
c) For completeness, let us mention that an example of an irreducible scheme that is not Lindelöf is the line with uncountably many origins, obtained from the disjoint union of uncountably many copies of the affine line by identifying them away from the origin.
When
![]() $\mathfrak {M}$
has a good filtration
$\mathfrak {M}$
has a good filtration
![]() $(\mathcal {U}_m)_{m \in \mathbb {N}}$
by finite type substacks, for fixed d, we have
$(\mathcal {U}_m)_{m \in \mathbb {N}}$
by finite type substacks, for fixed d, we have
for
![]() $m>d$
. This implies that, as long as we are interested in a fixed codimension, all computations can be carried out on a finite type stack, and thus essentially all results for the Chow groups of such stacks carry over (e.g., the excision sequence, including the version extended on the left by one higher Chow group from [Reference KreschKre99, Proposition 4.2.1]).
$m>d$
. This implies that, as long as we are interested in a fixed codimension, all computations can be carried out on a finite type stack, and thus essentially all results for the Chow groups of such stacks carry over (e.g., the excision sequence, including the version extended on the left by one higher Chow group from [Reference KreschKre99, Proposition 4.2.1]).
For stacks that are Lindelöf, we get at least the first three terms of the excision sequence.
Proposition A.5. Let
![]() $\mathfrak {M}$
be an equidimensional algebraic stack, locally finite type over a field k that is Lindelöf. Let
$\mathfrak {M}$
be an equidimensional algebraic stack, locally finite type over a field k that is Lindelöf. Let
![]() $j: \mathfrak {Z} \to \mathfrak {M}$
be a closed substack with complement
$j: \mathfrak {Z} \to \mathfrak {M}$
be a closed substack with complement
![]() $i: \mathfrak {V} = \mathfrak {M} \setminus \mathfrak {Z} \to \mathfrak {M}$
. Then there exists a complex
$i: \mathfrak {V} = \mathfrak {M} \setminus \mathfrak {Z} \to \mathfrak {M}$
. Then there exists a complex
that is exact at
![]() $\mathrm {CH}_*(\mathfrak {V})$
: that is,
$\mathrm {CH}_*(\mathfrak {V})$
: that is,
![]() $i^*$
is surjective. If moreover the stack
$i^*$
is surjective. If moreover the stack
![]() $\mathfrak {V}$
is a countable (finite or infinite) disjoint union of quotient stacks, the sequence is also exact at
$\mathfrak {V}$
is a countable (finite or infinite) disjoint union of quotient stacks, the sequence is also exact at
![]() $\mathrm {CH}_*(\mathfrak {M})$
.
$\mathrm {CH}_*(\mathfrak {M})$
.
Note that while the condition on
![]() $\mathfrak {V}$
being a countable union of quotient stacks might sound far-fetched, this is the situation we would encounter, for example, by taking
$\mathfrak {V}$
being a countable union of quotient stacks might sound far-fetched, this is the situation we would encounter, for example, by taking
![]() $\mathfrak {M}$
to be the boundary of the Picard stack
$\mathfrak {M}$
to be the boundary of the Picard stack
![]() $\mathfrak {Pic}_{g,n}$
and taking
$\mathfrak {Pic}_{g,n}$
and taking
![]() $\mathfrak {Z} \subset \mathfrak {M}$
the closed substack where the curve has at least
$\mathfrak {Z} \subset \mathfrak {M}$
the closed substack where the curve has at least
![]() $2$
nodes.
$2$
nodes.
Proof of Proposition A.5
Let
![]() $(\mathcal {U}_m)_{m \in \mathbb {N}}$
be an increasing cover of
$(\mathcal {U}_m)_{m \in \mathbb {N}}$
be an increasing cover of
![]() $\mathfrak {M}$
by finite type substacks. Denote by
$\mathfrak {M}$
by finite type substacks. Denote by
![]() $\mathfrak {M}_m, \mathfrak {Z}_m, \mathfrak {V}_m$
the intersections of
$\mathfrak {M}_m, \mathfrak {Z}_m, \mathfrak {V}_m$
the intersections of
![]() $\mathfrak {M}, \mathfrak {Z}, \mathfrak {V}$
with
$\mathfrak {M}, \mathfrak {Z}, \mathfrak {V}$
with
![]() $\mathcal {U}_m$
and by
$\mathcal {U}_m$
and by
![]() $j_m, i_m$
the restrictions of
$j_m, i_m$
the restrictions of
![]() $j,i$
. Then by the usual excision sequence for finite-type stacks, we have that
$j,i$
. Then by the usual excision sequence for finite-type stacks, we have that
are exact sequences. From another application of the excision sequence, we see that the restriction maps
are surjective. This implies that the system
![]() $(\mathrm {CH}_*(\mathfrak {Z}_m)/ \ker ((j_m)_*))_m$
is Mittag-Leffler (see [Sta20, Tag 0596]). Then it follows from [Sta20, Tag 0598] that we obtain an exact sequence
$(\mathrm {CH}_*(\mathfrak {Z}_m)/ \ker ((j_m)_*))_m$
is Mittag-Leffler (see [Sta20, Tag 0596]). Then it follows from [Sta20, Tag 0598] that we obtain an exact sequence
This finishes the proof of exactness of equation (38) at
![]() $\mathrm {CH}_*(\mathfrak {U})$
.
$\mathrm {CH}_*(\mathfrak {U})$
.
If
![]() $\mathfrak {V}$
is a countable disjoint union of quotient stacks, we can modify the exact sequence of equation (39), extending it to the left to obtain
$\mathfrak {V}$
is a countable disjoint union of quotient stacks, we can modify the exact sequence of equation (39), extending it to the left to obtain
We claim that the directed system
is Mittag-Leffler: that is, for m fixed, the images of the restriction maps
![]() $K_{m'} \to K_m$
stabilize for
$K_{m'} \to K_m$
stabilize for
![]() $m'\gg m$
. This follows from two easy observations:
$m'\gg m$
. This follows from two easy observations:
-
○ Since by construction
 $\mathfrak {V}_m = \mathfrak {V} \cap \mathcal {U}_m$
is of finite type, it is supported on a finite number of connected components
$\mathfrak {V}_m = \mathfrak {V} \cap \mathcal {U}_m$
is of finite type, it is supported on a finite number of connected components
 $\mathfrak {V}^1, \ldots , \mathfrak {V}^{e_m}$
of
$\mathfrak {V}^1, \ldots , \mathfrak {V}^{e_m}$
of
 $\mathfrak {V}$
.
$\mathfrak {V}$
. -
○ Since the stacks
 $\mathcal {U}_m$
cover
$\mathcal {U}_m$
cover
 $\mathfrak {M}$
, we know by Noetherian induction that for
$\mathfrak {M}$
, we know by Noetherian induction that for
 $m' \gg m$
the stack
$m' \gg m$
the stack
 $\mathfrak {V}_{m'}$
contains the union of
$\mathfrak {V}_{m'}$
contains the union of
 $\mathfrak {V}^1, \ldots , \mathfrak {V}^{e_m}$
, so we have
$\mathfrak {V}^1, \ldots , \mathfrak {V}^{e_m}$
, so we have  $$\begin{align*}K_{m'} = \bigoplus_{i=1}^{e_m} \mathrm{CH}_*(\mathfrak{V}^i, 1) \oplus \mathrm{CH}_*\left(\mathfrak{V}_{m'} \setminus \bigcup_{i=1}^{e_m} \mathfrak{V}^i , 1\right). \end{align*}$$
$$\begin{align*}K_{m'} = \bigoplus_{i=1}^{e_m} \mathrm{CH}_*(\mathfrak{V}^i, 1) \oplus \mathrm{CH}_*\left(\mathfrak{V}_{m'} \setminus \bigcup_{i=1}^{e_m} \mathfrak{V}^i , 1\right). \end{align*}$$
Under the map
![]() $K_{m'} \to K_m$
, the second direct summand always maps to zero (since it is supported on a different connected component). Thus indeed, for
$K_{m'} \to K_m$
, the second direct summand always maps to zero (since it is supported on a different connected component). Thus indeed, for
![]() $m' \gg m$
, the image of
$m' \gg m$
, the image of
![]() $K_{m'} \to K_m$
stabilizes to the image of the restriction morphism
$K_{m'} \to K_m$
stabilizes to the image of the restriction morphism
 $$\begin{align*}\bigoplus_{i=1}^{e_m} \mathrm{CH}_*(\mathfrak{V}^i, 1) \to \mathrm{CH}_*(\mathfrak{V}_m, 1) = K_m. \end{align*}$$
$$\begin{align*}\bigoplus_{i=1}^{e_m} \mathrm{CH}_*(\mathfrak{V}^i, 1) \to \mathrm{CH}_*(\mathfrak{V}_m, 1) = K_m. \end{align*}$$
We conclude that the system
![]() $(K_m)_m$
is Mittag-Leffler, so again using [Sta20, Tag 0598], we obtain an exact sequence
$(K_m)_m$
is Mittag-Leffler, so again using [Sta20, Tag 0598], we obtain an exact sequence
where we use that taking directed inverse limits is left-exact to identify the limit of
![]() $\ker (i_m^*)$
as
$\ker (i_m^*)$
as
![]() $\ker (i^*)$
. Thus we conclude that
$\ker (i^*)$
. Thus we conclude that
![]() $\mathrm {CH}_*(\mathfrak {Z})$
surjects onto the kernel of
$\mathrm {CH}_*(\mathfrak {Z})$
surjects onto the kernel of
![]() $i^*$
, obtaining exactness of equation (38) at
$i^*$
, obtaining exactness of equation (38) at
![]() $\mathrm {CH}_*(\mathfrak {M})$
.
$\mathrm {CH}_*(\mathfrak {M})$
.
Remark A.6. In the context of algebraic spaces, a different definition of Chow groups for locally finite type spaces is presented in [Sta20, Tag 0EDZ]. It works directly with formal linear combinations of cycles where locally only finitely many of the coefficients are nonzero. We expect that by adapting the definitions of [Reference KreschKre99], one can give a similar definition in the case of algebraic stacks locally of finite type. It seems likely that for stacks that are far away from being finite type (e.g., stacks not being Lindelöf), these alternative Chow groups have better formal properties than the groups we construct, since, for example, in the setting of algebraic spaces, they satisfy an excision sequence without such assumptions on the ambient space (see [Sta20, Tag 0EP9]). The advantage of Definition A.1 is that it does not require us to reprove the standard constructions and properties of Chow groups since they descend easily to the projective limit. We do expect that the alternative definition of Chow groups modeled on [Sta20, Tag 0EDZ] coincides with our definition for algebraic stacks locally of finite type over a field that have good filtration by finite type substacks.
B Proper pushforward of cycles (jointly with J. Skowera)
It is known that algebraic stacks of finite type over a field that can be stratified by locally closed substacks that are global quotient stacks admit an intersection theory with integral coefficients. The theory includes a pushforward operation for projective morphisms [Reference KreschKre99]. In the definition of the tautological ring, we frequently use pushforwards along forgetful and morphisms. For the moduli stacks of prestable curves, these morphisms are proper but not projective. A priori, this is a problem. Here we show that the pushforward operation for integral coefficients may be extended to proper representable morphisms. If the coefficients are rational, there is also a pushforward for morphisms of relative Deligne-Mumford type.
B.1 Definitions and terminologies
Let a base field k be fixed. In this section, stacks are algebraic stacks of finite type over k. All morphisms are morphisms over k. A morphism of stacks
![]() $X \to Y$
is projective if it can be factored up to 2-isomorphism through a closed immersion into the projective bundle
$X \to Y$
is projective if it can be factored up to 2-isomorphism through a closed immersion into the projective bundle
![]() $\mathbb {P}(\mathcal {E}) \to Y$
for a coherent sheaf
$\mathbb {P}(\mathcal {E}) \to Y$
for a coherent sheaf
![]() $\mathcal {E}$
of
$\mathcal {E}$
of
![]() $\mathcal {O}_Y$
-modules.
$\mathcal {O}_Y$
-modules.
We briefly recall the construction of the Chow groups of an algebraic stack Y of finite type over k. A representative of a d-cycle is a pair
![]() $(f, \alpha )$
for a projective morphism
$(f, \alpha )$
for a projective morphism
![]() $f : X \to Y$
from an algebraic stack X and a naive cycle
$f : X \to Y$
from an algebraic stack X and a naive cycle
![]() $\alpha \in \mathrm {CH}^{\circ }_{d+\mathrm {rk}\, E}(E)$
on a vector bundle
$\alpha \in \mathrm {CH}^{\circ }_{d+\mathrm {rk}\, E}(E)$
on a vector bundle
![]() $E \to X$
of constant rank. The Chow groups of Y are
$E \to X$
of constant rank. The Chow groups of Y are
 $$\begin{align*}\mathrm{CH}_d(Y) = \varinjlim_{X \to Y \in \mathfrak{A}_{Y}} \left[ \widehat{\mathrm{CH}}_d (X) / \widehat{B}_d (X) \right] \end{align*}$$
$$\begin{align*}\mathrm{CH}_d(Y) = \varinjlim_{X \to Y \in \mathfrak{A}_{Y}} \left[ \widehat{\mathrm{CH}}_d (X) / \widehat{B}_d (X) \right] \end{align*}$$
where
 $$ \begin{align*} \widehat{\mathrm{CH}}_d(X) & = \varinjlim_{E \in \mathfrak{B}_X} \mathrm{CH}_{d+\mathrm{rk}\, E}^{\circ} E \\ \mathrm{CH}_d^{\circ}(E) & = Z_d(E) / \delta \mathrm{Rat}_{d}(E) \\ Z_d(E) & = d\textrm{-dimensional cycles} \\ \mathrm{Rat}_{d}(E) & = \bigoplus_Z k(Z)^{*}, Z \subset E \text{ integral closed }, \dim Z = d+1 \\ Ob(\mathfrak{A}_Y) & = \{ X \to Y \mid \textrm{ projective} \} \\ Mor(X, X') & = \{ X \to X' \mid Y\textrm{-isom. onto an open and closed substack of } X' \} \\ Ob(\mathfrak{B}_X) & = \{ E \to X \mid \textrm{ vector bundle of constant rank} \} \\ Mor(E, F) & = \{ E \to F \mid \textrm{ surjective vector bundle morphism}\}. \end{align*} $$
$$ \begin{align*} \widehat{\mathrm{CH}}_d(X) & = \varinjlim_{E \in \mathfrak{B}_X} \mathrm{CH}_{d+\mathrm{rk}\, E}^{\circ} E \\ \mathrm{CH}_d^{\circ}(E) & = Z_d(E) / \delta \mathrm{Rat}_{d}(E) \\ Z_d(E) & = d\textrm{-dimensional cycles} \\ \mathrm{Rat}_{d}(E) & = \bigoplus_Z k(Z)^{*}, Z \subset E \text{ integral closed }, \dim Z = d+1 \\ Ob(\mathfrak{A}_Y) & = \{ X \to Y \mid \textrm{ projective} \} \\ Mor(X, X') & = \{ X \to X' \mid Y\textrm{-isom. onto an open and closed substack of } X' \} \\ Ob(\mathfrak{B}_X) & = \{ E \to X \mid \textrm{ vector bundle of constant rank} \} \\ Mor(E, F) & = \{ E \to F \mid \textrm{ surjective vector bundle morphism}\}. \end{align*} $$
The subgroup
![]() $\widehat {B}_d (X)$
is defined to be
$\widehat {B}_d (X)$
is defined to be
 $$ \begin{align*} \widehat{B}_d(X) = \coprod_{\begin{subarray}{c} p_1, p_2 : W \to X \\ g \circ p_1 \cong g \circ p_2 \end{subarray}} \coprod_{E, F \in \mathfrak{B}_{X}} Z_{E, F}, \end{align*} $$
$$ \begin{align*} \widehat{B}_d(X) = \coprod_{\begin{subarray}{c} p_1, p_2 : W \to X \\ g \circ p_1 \cong g \circ p_2 \end{subarray}} \coprod_{E, F \in \mathfrak{B}_{X}} Z_{E, F}, \end{align*} $$
 $$ \begin{align*} Z_{E, F} = \left\{ p_{2*}\beta_2 - p_{1*}\beta_1 \left| \begin{array}{c} \beta_1 \in \mathrm{CH}_{d+\mathrm{rk}\, E}^{\circ}(p_1^{*}E), \quad \beta_2 \in \mathrm{CH}_{d+\mathrm{rk}\, F}^{\circ}(p_2^{*}F) \\ \beta_1 \sim \beta_2 \textrm{ in } \widehat{\mathrm{CH}}_d(W) \end{array} \right. \right\} \end{align*} $$
$$ \begin{align*} Z_{E, F} = \left\{ p_{2*}\beta_2 - p_{1*}\beta_1 \left| \begin{array}{c} \beta_1 \in \mathrm{CH}_{d+\mathrm{rk}\, E}^{\circ}(p_1^{*}E), \quad \beta_2 \in \mathrm{CH}_{d+\mathrm{rk}\, F}^{\circ}(p_2^{*}F) \\ \beta_1 \sim \beta_2 \textrm{ in } \widehat{\mathrm{CH}}_d(W) \end{array} \right. \right\} \end{align*} $$
where the first union is over projective morphisms and introduces a dependence on the morphism
![]() $g : X \to Y$
through the constraint
$g : X \to Y$
through the constraint
![]() $g \circ p_1 \cong g \circ p_2$
. This accomplishes in a single step what the original definition [Reference KreschKre99, Definition 2.1.4(iii)] does in two by assuming the vector bundles to be of constant rank.
$g \circ p_1 \cong g \circ p_2$
. This accomplishes in a single step what the original definition [Reference KreschKre99, Definition 2.1.4(iii)] does in two by assuming the vector bundles to be of constant rank.
The above definition facilitates projective pushforwards: the cycle
![]() $(g, \alpha )$
pushes forward under f to
$(g, \alpha )$
pushes forward under f to
![]() $(f\circ g, \alpha )$
. A projective morphism
$(f\circ g, \alpha )$
. A projective morphism
![]() $S \to U$
to an open substack
$S \to U$
to an open substack
![]() $U \subset Y$
can be realized as the pullback of a projective morphism to Y [Reference KreschKre99, Corollary 2.3.2]. It is unknown whether this property can be extended to proper morphisms.
$U \subset Y$
can be realized as the pullback of a projective morphism to Y [Reference KreschKre99, Corollary 2.3.2]. It is unknown whether this property can be extended to proper morphisms.
Definition B.1. Let
![]() $f : X \to Y$
be a morphism of algebraic stacks. We further define restricted Chow groups formed from the pullbacks of vector bundles,
$f : X \to Y$
be a morphism of algebraic stacks. We further define restricted Chow groups formed from the pullbacks of vector bundles,
 $$ \begin{align*} \mathrm{CH}^f_d (X) = \varinjlim_{Y' \to Y \in \mathfrak{A}_{Y}} \left[ \widehat{\mathrm{CH}}_d^{f'} \left( X' \right) / \widehat{B}_d^{f'} \left( X' \right) \right], \end{align*} $$
$$ \begin{align*} \mathrm{CH}^f_d (X) = \varinjlim_{Y' \to Y \in \mathfrak{A}_{Y}} \left[ \widehat{\mathrm{CH}}_d^{f'} \left( X' \right) / \widehat{B}_d^{f'} \left( X' \right) \right], \end{align*} $$
where
![]() $f' : X' \to Y'$
is the pullback of f by the projective morphism
$f' : X' \to Y'$
is the pullback of f by the projective morphism
![]() $Y' \to Y$
. Recall that the restricted Edidin–Graham–Totaro Chow groups [Reference KreschKre99, Definition 2.1.4(iv)] are the groups defined by
$Y' \to Y$
. Recall that the restricted Edidin–Graham–Totaro Chow groups [Reference KreschKre99, Definition 2.1.4(iv)] are the groups defined by
 $$ \begin{align} \widehat{\mathrm{CH}}^{f'}_d (X') = \varinjlim_{E \in \mathfrak{B}_{Y'}}\mathrm{CH}^{\circ}_{d + \mathrm{rk}\, E} (f^{'*} E). \end{align} $$
$$ \begin{align} \widehat{\mathrm{CH}}^{f'}_d (X') = \varinjlim_{E \in \mathfrak{B}_{Y'}}\mathrm{CH}^{\circ}_{d + \mathrm{rk}\, E} (f^{'*} E). \end{align} $$
The quotient group
 $$\begin{align*}\widehat{B}_d^{f'}X' = \coprod_{\begin{subarray}{c} p_1, p_2 : W \to Y' \\ g \circ p_1 \cong g \circ p_2 \end{subarray}} \coprod_{E,F \in \mathfrak{B}_{Y'}} Z_{E, F}^f, \end{align*}$$
$$\begin{align*}\widehat{B}_d^{f'}X' = \coprod_{\begin{subarray}{c} p_1, p_2 : W \to Y' \\ g \circ p_1 \cong g \circ p_2 \end{subarray}} \coprod_{E,F \in \mathfrak{B}_{Y'}} Z_{E, F}^f, \end{align*}$$
where
 $$\begin{align*}Z_{E, F}^f = \left\{p_{2*}' \beta_2 - p_{1*}' \beta_1 \left| \begin{array}{c} \beta_1 \in \mathrm{CH}^{\circ}_{d + \mathrm{rk}\, E}({p'}_1^{*}{f'}^{*}E), \,\beta_2 \in \mathrm{CH}^{\circ}_{d + \mathrm{rk}\, F}({p'}_2^{*}{f'}^{*}F) \\ \beta_1 \sim \beta_2 \textrm{ in } \widehat{\mathrm{CH}}_d^{f''}(W') \end{array} \right. \right\}, \end{align*}$$
$$\begin{align*}Z_{E, F}^f = \left\{p_{2*}' \beta_2 - p_{1*}' \beta_1 \left| \begin{array}{c} \beta_1 \in \mathrm{CH}^{\circ}_{d + \mathrm{rk}\, E}({p'}_1^{*}{f'}^{*}E), \,\beta_2 \in \mathrm{CH}^{\circ}_{d + \mathrm{rk}\, F}({p'}_2^{*}{f'}^{*}F) \\ \beta_1 \sim \beta_2 \textrm{ in } \widehat{\mathrm{CH}}_d^{f''}(W') \end{array} \right. \right\}, \end{align*}$$
depends on the notation,

Recall that we only consider vector bundles of constant rank. Therefore a cycle in
![]() $\mathrm {CH}^f_d (X)$
is represented by
$\mathrm {CH}^f_d (X)$
is represented by
![]() $(g, \alpha ')$
,
$(g, \alpha ')$
,
![]() $\alpha ' \in \mathrm {CH}^{\circ }_{d + \mathrm {rk}\, E'} (E')$
as in the pullback diagram
$\alpha ' \in \mathrm {CH}^{\circ }_{d + \mathrm {rk}\, E'} (E')$
as in the pullback diagram

There is a natural morphism from the restricted Chow groups to the usual Chow groups
When f is proper and representable, the cycles in
![]() $\mathrm {CH}_d^f(X)$
can be pushed forward between naive Chow groups by direct generalization of the definition of pushforward for Deligne-Mumford stacks [Reference VistoliVis89, Definition 3.6]. If E is a vector bundle on
$\mathrm {CH}_d^f(X)$
can be pushed forward between naive Chow groups by direct generalization of the definition of pushforward for Deligne-Mumford stacks [Reference VistoliVis89, Definition 3.6]. If E is a vector bundle on
![]() $Y'$
, then
$Y'$
, then
![]() $f_*$
pushes the class represented by a cycle
$f_*$
pushes the class represented by a cycle
![]() $\alpha \in \mathrm {CH}^{\circ }_*(E')$
forward to
$\alpha \in \mathrm {CH}^{\circ }_*(E')$
forward to
![]() ${f''}_*(\alpha ) \in \mathrm {CH}^{\circ }_*(E)$
in the notation of the diagram in equation (42).
${f''}_*(\alpha ) \in \mathrm {CH}^{\circ }_*(E)$
in the notation of the diagram in equation (42).
Lemma B.2. If
![]() $f : X \to Y$
is a proper, representable morphism, then there is a proper pushforward
$f : X \to Y$
is a proper, representable morphism, then there is a proper pushforward
![]() $f_* : \mathrm {CH}^f_d(X) \to \mathrm {CH}_d (Y)$
for all d.
$f_* : \mathrm {CH}^f_d(X) \to \mathrm {CH}_d (Y)$
for all d.
A morphism
![]() $f : X \to Y$
of stacks is of relative Deligne-Mumford type if any morphism
$f : X \to Y$
of stacks is of relative Deligne-Mumford type if any morphism
![]() $T\to Y$
from a scheme T to Y pulls back to a Deligne-Mumford stack
$T\to Y$
from a scheme T to Y pulls back to a Deligne-Mumford stack
![]() $X\times _Y T$
. Note that representable morphisms are of relative Deligne-Mumford type. The proper pushforward of naive Chow groups
$X\times _Y T$
. Note that representable morphisms are of relative Deligne-Mumford type. The proper pushforward of naive Chow groups
![]() $\mathrm {CH}^{\circ }(-)_{\mathbb {Q}}$
along a relative Deligne-Mumford type morphism is defined as follows: for
$\mathrm {CH}^{\circ }(-)_{\mathbb {Q}}$
along a relative Deligne-Mumford type morphism is defined as follows: for
![]() $f\colon X\to Y$
a relative Deligne-Mumford type, proper morphism between algebraic stacks, we construct a pushforward map
$f\colon X\to Y$
a relative Deligne-Mumford type, proper morphism between algebraic stacks, we construct a pushforward map
To define equation (43), the degree of f defined in [Reference VistoliVis89] should be extended to this setting. We first consider the case when X is an integral algebraic stack and Y is the image of f. For a smooth surjective morphism
![]() $u: U\to Y$
from an integral scheme U, consider the Cartesian diagram
$u: U\to Y$
from an integral scheme U, consider the Cartesian diagram

Since f is a relative Deligne-Mumford type, the fibre product
![]() $U_X$
is a Deligne-Mumford stack. Moreover,
$U_X$
is a Deligne-Mumford stack. Moreover,
![]() $U_X$
is reduced because
$U_X$
is reduced because
![]() $U_X\to X$
is smooth, and X is reduced. Let
$U_X\to X$
is smooth, and X is reduced. Let
![]() $U_X= \cup _i U_i$
be a finite number of irreducible components of U, and let
$U_X= \cup _i U_i$
be a finite number of irreducible components of U, and let
![]() $f_i'\colon U_i\to U$
be the restriction of
$f_i'\colon U_i\to U$
be the restriction of
![]() $f'$
to each irreducible component. We define
$f'$
to each irreducible component. We define
 $$\begin{align*}\deg f =\begin{cases} \sum_i \deg f^{\prime}_i,& \text{ when } \dim X = \dim Y \\ 0,& \text{ otherwise} \end{cases}\end{align*}$$
$$\begin{align*}\deg f =\begin{cases} \sum_i \deg f^{\prime}_i,& \text{ when } \dim X = \dim Y \\ 0,& \text{ otherwise} \end{cases}\end{align*}$$
where
![]() $\deg f^{\prime }_i$
is the degree of
$\deg f^{\prime }_i$
is the degree of
![]() $f^{\prime }_i$
between Deligne-Mumford stacks defined in [Reference VistoliVis89].Footnote
17
This definition is independent of the choice of a smooth atlas u. For an arbitrary
$f^{\prime }_i$
between Deligne-Mumford stacks defined in [Reference VistoliVis89].Footnote
17
This definition is independent of the choice of a smooth atlas u. For an arbitrary
![]() $\mathbb {Q}$
-linear combination of integral cycles
$\mathbb {Q}$
-linear combination of integral cycles
![]() $Z=\sum _j a_j\cdot Z_j$
, the map in equation (43) is defined by
$Z=\sum _j a_j\cdot Z_j$
, the map in equation (43) is defined by
It is straightforward to check that
![]() $f_*$
is functorial.
$f_*$
is functorial.
Similarly, we can define a proper pushforward
on the space of rational equivalences. Let
![]() $Z \subseteq X$
be an integral closed substack of dimension
$Z \subseteq X$
be an integral closed substack of dimension
![]() $d+1$
, and let
$d+1$
, and let
![]() $\varphi \in k(Z)^*$
, giving an element
$\varphi \in k(Z)^*$
, giving an element
![]() $(Z, \varphi ) \in \mathrm {Rat}_d(Y)$
. Then for
$(Z, \varphi ) \in \mathrm {Rat}_d(Y)$
. Then for
![]() $Z'=f(Z)\subseteq Y$
, we set
$Z'=f(Z)\subseteq Y$
, we set
![]() $f_*(Z, \varphi )=0$
if
$f_*(Z, \varphi )=0$
if
![]() $\dim Z'<\dim Z$
and
$\dim Z'<\dim Z$
and
![]() $f_*(Z, \varphi )=(Z',N_{k(Z)/k(Z')}(\varphi ))$
otherwise, where
$f_*(Z, \varphi )=(Z',N_{k(Z)/k(Z')}(\varphi ))$
otherwise, where
![]() $N_{k(Z)/k(Z')}$
is the norm map of the finite field extension
$N_{k(Z)/k(Z')}$
is the norm map of the finite field extension
![]() $k(Z)/k(Z')$
.
$k(Z)/k(Z')$
.
Before continuing, we want to argue that this pushforward of rational equivalences is compatible with taking smooth covers. Indeed, given a smooth surjective morphism
![]() $U \to Y$
of relative dimension e, consider the fibre diagram
$U \to Y$
of relative dimension e, consider the fibre diagram

Pullbacks to
![]() $U,V$
induce maps
$U,V$
induce maps
![]() $\mathrm {Rat}_*(Y) \to \mathrm {Rat}_{*+e}(U)$
and
$\mathrm {Rat}_*(Y) \to \mathrm {Rat}_{*+e}(U)$
and
![]() $\mathrm {Rat}_*(X) \to \mathrm {Rat}_{*+e}(V)$
, and we claim that the natural diagram
$\mathrm {Rat}_*(X) \to \mathrm {Rat}_{*+e}(V)$
, and we claim that the natural diagram

commutes. To see this, let
![]() $Z \subseteq X$
be an integral closed substack, write
$Z \subseteq X$
be an integral closed substack, write
![]() $Z'=f(Z)$
and denote by
$Z'=f(Z)$
and denote by
![]() $Z_V, Z^{\prime }_U$
their preimages in
$Z_V, Z^{\prime }_U$
their preimages in
![]() $V,U$
. Then
$V,U$
. Then
![]() $\dim (Z')<\dim (Z)$
if and only if
$\dim (Z')<\dim (Z)$
if and only if
![]() $\dim (Z^{\prime }_U)<\dim (Z_V)$
. On the other hand, when we have equality of dimensions and denote by
$\dim (Z^{\prime }_U)<\dim (Z_V)$
. On the other hand, when we have equality of dimensions and denote by
![]() $Z_{V,i}, Z^{\prime }_{U,i}$
the irreducible components of
$Z_{V,i}, Z^{\prime }_{U,i}$
the irreducible components of
![]() $Z_V, Z^{\prime }_U$
, it holds that
$Z_V, Z^{\prime }_U$
, it holds that
![]() $k(Z_{V,i}) = k(Z) \otimes _{k(Z')} k(Z^{\prime }_{U,i})$
. Then we claim that for
$k(Z_{V,i}) = k(Z) \otimes _{k(Z')} k(Z^{\prime }_{U,i})$
. Then we claim that for
![]() $\varphi \in k(Z)$
, we have
$\varphi \in k(Z)$
, we have
which finishes the proof of the commutativity of the diagram in equation (44). But indeed, the claim in equation (45) follows from the definition of the norm, since the determinant of an endomorphism of a vector space over some field K is unchanged by tensoring with an extension field of K.
Lemma B.3. The pushforward
![]() $f_*$
commutes with the boundary map
$f_*$
commutes with the boundary map
![]() $\delta $
and thus passes through rational equivalence.
$\delta $
and thus passes through rational equivalence.
Proof. We first argue that it is enough to prove the compatibility on a smooth atlas of Y. Let
![]() $U\to Y$
be a smooth atlas of relative dimension e; then we have a commutative diagram
$U\to Y$
be a smooth atlas of relative dimension e; then we have a commutative diagram

where the rows are equalizer sequences. There is a similar diagram for the induced map
![]() $U \times _Y X \to X$
, and this diagram maps to the diagram above via the proper pushforward
$U \times _Y X \to X$
, and this diagram maps to the diagram above via the proper pushforward
![]() $f_*$
. But then, due to the injectivity of the map
$f_*$
. But then, due to the injectivity of the map
![]() $Z_*(Y) \to Z_{*+e}(U)$
, the claimed equality of maps
$Z_*(Y) \to Z_{*+e}(U)$
, the claimed equality of maps
can be checked on U. Thus we can reduce to checking the lemma for a target that is a scheme, in which case the corresponding argument was given in the proof of [Reference VistoliVis89, Proposition 3.7].Footnote 18
B.2 Properties of restricted Chow groups
Definition B.4 ([Reference TotaroTot99])
An approximating vector bundle of X in codimension d is a vector bundle
![]() $E \to X$
such that
$E \to X$
such that
![]() $E \setminus S$
is an algebraic space for a closed substack S with
$E \setminus S$
is an algebraic space for a closed substack S with
![]() $\mathrm {codim}_E S> d$
. It is called approximating, because
$\mathrm {codim}_E S> d$
. It is called approximating, because
![]() $\mathrm {CH}_j(X) {\stackrel {\sim }{\longrightarrow }} \mathrm {CH}^{\circ }_{j+\mathrm {rk}\, E}(E)$
for large enough j ([Reference KreschKre99, Corollary 2.4.9]).
$\mathrm {CH}_j(X) {\stackrel {\sim }{\longrightarrow }} \mathrm {CH}^{\circ }_{j+\mathrm {rk}\, E}(E)$
for large enough j ([Reference KreschKre99, Corollary 2.4.9]).
Let
![]() $X = [\widehat {X}/G]$
be a global quotient stack. Then for any d, X has an approximating vector bundle in codimension d, which is the pullback of
$X = [\widehat {X}/G]$
be a global quotient stack. Then for any d, X has an approximating vector bundle in codimension d, which is the pullback of
![]() $\mathrm {Hom}_k(k^{N+n}, W)$
from
$\mathrm {Hom}_k(k^{N+n}, W)$
from
![]() $BG$
for a faithful representation W of G of dimension n and N large ([Reference TotaroTot99, Remark 1.4]).
$BG$
for a faithful representation W of G of dimension n and N large ([Reference TotaroTot99, Remark 1.4]).
Lemma B.5. Let
![]() $f: X \to Y$
be a representable morphism. Let
$f: X \to Y$
be a representable morphism. Let
![]() $(g, \alpha )$
be a cycle in
$(g, \alpha )$
be a cycle in
![]() $\mathrm {CH}_d(X)$
or
$\mathrm {CH}_d(X)$
or
![]() $\mathrm {CH}^f_d(X)$
, and let F be an approximating vector bundle of X in codimension D, respectively the pullback by f of an approximating vector bundle on Y in codimension D. When D is sufficiently large, we have
$\mathrm {CH}^f_d(X)$
, and let F be an approximating vector bundle of X in codimension D, respectively the pullback by f of an approximating vector bundle on Y in codimension D. When D is sufficiently large, we have
![]() $(g, \alpha ) \sim (1_X, \delta )$
for some naive cycle
$(g, \alpha ) \sim (1_X, \delta )$
for some naive cycle
![]() $\delta \in \mathrm {CH}^{\circ }_{d + \mathrm {rk}\, F}(F)$
. In fact, the natural map
$\delta \in \mathrm {CH}^{\circ }_{d + \mathrm {rk}\, F}(F)$
. In fact, the natural map
![]() $\mathrm {CH}^{\circ } _{d+\mathrm {rk}\, F}(F) \to \mathrm {CH}_d(X), \delta \mapsto (1_X, \delta )$
is an isomorphism.
$\mathrm {CH}^{\circ } _{d+\mathrm {rk}\, F}(F) \to \mathrm {CH}_d(X), \delta \mapsto (1_X, \delta )$
is an isomorphism.
Proof. We consider the case of
![]() $\mathrm {CH}_d(X)$
; the case of
$\mathrm {CH}_d(X)$
; the case of
![]() $\mathrm {CH}^f_d(X)$
is analogous. Let
$\mathrm {CH}^f_d(X)$
is analogous. Let
![]() $\alpha \in \mathrm {CH}_{d+\mathrm {rk}\, E}^{\circ } (E)$
be a representative of a cycle in
$\alpha \in \mathrm {CH}_{d+\mathrm {rk}\, E}^{\circ } (E)$
be a representative of a cycle in
![]() $\mathrm {CH}_d(X)$
. Consider the following Cartesian diagram:
$\mathrm {CH}_d(X)$
. Consider the following Cartesian diagram:

Let
![]() $S\subset F$
be a closed substack with
$S\subset F$
be a closed substack with
![]() $\mathrm {codim}_F S>D$
and such that
$\mathrm {codim}_F S>D$
and such that
![]() $F\setminus S$
is an algebraic space. Then the intersection of S with any fibre of
$F\setminus S$
is an algebraic space. Then the intersection of S with any fibre of
![]() $F \to X$
has codimension at least
$F \to X$
has codimension at least
![]() $D-\dim (X)$
inside the fibre, and thus, after taking the Cartesian diagram with
$D-\dim (X)$
inside the fibre, and thus, after taking the Cartesian diagram with
![]() $g: X' \to X$
, we have
$g: X' \to X$
, we have
Moreover, since s is projective, we know that H is an algebraic space away from
![]() $s^{-1}(S)$
. Let
$s^{-1}(S)$
. Let
![]() $r = \mathrm {rk}\, F$
; then for
$r = \mathrm {rk}\, F$
; then for
![]() $D>\dim (X)+\dim (X')-d$
, we have that
$D>\dim (X)+\dim (X')-d$
, we have that
![]() $\mathrm {CH}_{d+r}(H) \cong \mathrm {CH}_{d+r}^{\circ }(H)$
and likewise
$\mathrm {CH}_{d+r}(H) \cong \mathrm {CH}_{d+r}^{\circ }(H)$
and likewise
![]() $\mathrm {CH}_{d+r+\mathrm {rk}\, E}(E \oplus H) \cong \mathrm {CH}_{d+r+\mathrm {rk}\, E}^{\circ }(E \oplus H)$
. Since the pullback
$\mathrm {CH}_{d+r+\mathrm {rk}\, E}(E \oplus H) \cong \mathrm {CH}_{d+r+\mathrm {rk}\, E}^{\circ }(E \oplus H)$
. Since the pullback
![]() $q^*$
on the usual Chow groups is an isomorphism by [Reference KreschKre99, Theorem 2.1.12 (vi)], we conclude that
$q^*$
on the usual Chow groups is an isomorphism by [Reference KreschKre99, Theorem 2.1.12 (vi)], we conclude that
is an isomorphism.
Now, starting with the cycle
![]() $\alpha $
on E, we have that
$\alpha $
on E, we have that
![]() $\beta =p^*\alpha $
is a cycle on
$\beta =p^*\alpha $
is a cycle on
![]() $E\oplus H$
. Since the map
$E\oplus H$
. Since the map
![]() $q^*$
above is an isomorphism, there exists a unique
$q^*$
above is an isomorphism, there exists a unique
![]() $\gamma \in \mathrm {CH}_{d+r}^{\circ }(H)$
such that
$\gamma \in \mathrm {CH}_{d+r}^{\circ }(H)$
such that
![]() $\beta = q^{*}\gamma $
. Then on the one hand we have
$\beta = q^{*}\gamma $
. Then on the one hand we have
![]() $(g, \alpha ) \sim (g, \beta ) \sim (g, \gamma )$
by [Reference KreschKre99, Remark 2.1.5]. On the other hand, defining
$(g, \alpha ) \sim (g, \beta ) \sim (g, \gamma )$
by [Reference KreschKre99, Remark 2.1.5]. On the other hand, defining
![]() $\delta = s_{*}\gamma $
we have
$\delta = s_{*}\gamma $
we have
![]() $(g, \gamma ) \sim (1_X, \delta )$
as in [Reference KreschKre99, Remark 2.1.16], concluding the proof. Going through this construction, the association
$(g, \gamma ) \sim (1_X, \delta )$
as in [Reference KreschKre99, Remark 2.1.16], concluding the proof. Going through this construction, the association
![]() $(g,\alpha ) \mapsto (1_X, \delta )$
gives a well-defined map, and it is immediate to check that it gives the inverse to the natural homomorphism
$(g,\alpha ) \mapsto (1_X, \delta )$
gives a well-defined map, and it is immediate to check that it gives the inverse to the natural homomorphism
![]() $\mathrm {CH}^{\circ } _{d+\mathrm {rk}\, F}(F) \to \mathrm {CH}_d(X)$
.
$\mathrm {CH}^{\circ } _{d+\mathrm {rk}\, F}(F) \to \mathrm {CH}_d(X)$
.
Proposition B.6. If Y is a global quotient stack and
![]() $f : X \to Y$
is representable, then for all d, the natural morphism
$f : X \to Y$
is representable, then for all d, the natural morphism
![]() $\iota _f: \mathrm {CH}^f_d(X) \to \mathrm {CH}_d(X)$
is an isomorphism.
$\iota _f: \mathrm {CH}^f_d(X) \to \mathrm {CH}_d(X)$
is an isomorphism.
Proof. In the notation of equation (42), let F be the pullback of an approximating vector bundle on Y. Then
![]() $\iota _f$
factors as
$\iota _f$
factors as
The association
![]() $(g, \alpha ) \mapsto (1_X, \delta )$
of Lemma B.5 defines the first isomorphism. Its inverse is the inclusion
$(g, \alpha ) \mapsto (1_X, \delta )$
of Lemma B.5 defines the first isomorphism. Its inverse is the inclusion
![]() $\mathrm {CH}^{\circ }_{d+\mathrm {rk}\, F}(F) \to \mathrm {CH}^f_d(X)$
. The second map is an isomorphism because F is an algebraic space in dimension
$\mathrm {CH}^{\circ }_{d+\mathrm {rk}\, F}(F) \to \mathrm {CH}^f_d(X)$
. The second map is an isomorphism because F is an algebraic space in dimension
![]() $d+\mathrm {rk}\, F$
([Reference KreschKre99, Theorem 2.1.12(i)]). The third map is an isomorphism by homotopy invariance [Reference KreschKre99, Corollary 2.4.9].
$d+\mathrm {rk}\, F$
([Reference KreschKre99, Theorem 2.1.12(i)]). The third map is an isomorphism by homotopy invariance [Reference KreschKre99, Corollary 2.4.9].
Proposition B.7. If
![]() $f : X \to Y$
is of relative Deligne-Mumford type and Y is a global quotient stack, then the natural morphism
$f : X \to Y$
is of relative Deligne-Mumford type and Y is a global quotient stack, then the natural morphism
![]() $\iota _f : \mathrm {CH}^f_d(X, \mathbb {Q}) \to \mathrm {CH}_d(X, \mathbb {Q})$
is an isomorphism for all d.
$\iota _f : \mathrm {CH}^f_d(X, \mathbb {Q}) \to \mathrm {CH}_d(X, \mathbb {Q})$
is an isomorphism for all d.
Proof. By the fact that
![]() $\mathrm {CH}^{\circ }_d(X, \mathbb {Q}) \cong \mathrm {CH}_d(X, \mathbb {Q})$
for any Deligne-Mumford stack X [Reference KreschKre99, Theorem 2.1.12(ii)], the morphism
$\mathrm {CH}^{\circ }_d(X, \mathbb {Q}) \cong \mathrm {CH}_d(X, \mathbb {Q})$
for any Deligne-Mumford stack X [Reference KreschKre99, Theorem 2.1.12(ii)], the morphism
![]() $\iota _f$
factors in the same way as
$\iota _f$
factors in the same way as
![]() $\iota _f$
in Proposition B.6 over
$\iota _f$
in Proposition B.6 over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Let
![]() $f:X\to Y$
be a proper morphism of relative Deligne-Mumford type, and let
$f:X\to Y$
be a proper morphism of relative Deligne-Mumford type, and let
![]() $h:W\to Y$
be a morphism of algebraic stacks. Consider the following Cartesian diagram:
$h:W\to Y$
be a morphism of algebraic stacks. Consider the following Cartesian diagram:

For each d, the groups
![]() $\mathrm {CH}^f_d (X)$
satisfy the following properties:
$\mathrm {CH}^f_d (X)$
satisfy the following properties:
-
(i) Let the above morphism
 $h:W \to Y$
be a flat morphism of relative dimension r. Then there is a functorial pullback homomorphism
$h:W \to Y$
be a flat morphism of relative dimension r. Then there is a functorial pullback homomorphism
 $\mathrm {CH}^f_d(X) \to \mathrm {CH}^{\tilde {f}}_{d+r}(V)$
.
$\mathrm {CH}^f_d(X) \to \mathrm {CH}^{\tilde {f}}_{d+r}(V)$
. -
(ii) Let the above morphism
 $h:W \to Y$
be a projective morphism; then there is a functorial pushforward homomorphism
$h:W \to Y$
be a projective morphism; then there is a functorial pushforward homomorphism
 $\mathrm {CH}^{\tilde {f}}_d(V) \to \mathrm {CH}^f_d(X)$
.
$\mathrm {CH}^{\tilde {f}}_d(V) \to \mathrm {CH}^f_d(X)$
. -
(iii) The homomorphisms (i) and (ii) are compatible with the natural morphism from restricted Chow groups to the usual Chow groups; that is, we have commutative diagrams

Proposition B.8 (Excision)
Let
![]() $i : Z \to Y$
be a closed substack, and
$i : Z \to Y$
be a closed substack, and
![]() $j : U \to Y$
its complement. Let
$j : U \to Y$
its complement. Let
![]() $Z' \to X$
be the preimage of Z under f, and let
$Z' \to X$
be the preimage of Z under f, and let
![]() $U'$
be its complement. Let
$U'$
be its complement. Let
![]() $f' = f|_{Z'}$
and
$f' = f|_{Z'}$
and
![]() $\widetilde {f} = f|_{U'}$
:
$\widetilde {f} = f|_{U'}$
:

Then for each d, the flat pullback and projective pushforward fit together into an exact sequence
Proof. This is [Reference KreschKre99, Proposition 2.3.6] where constructions are performed in the lower level
![]() $(Y, Z, U)$
and pulled back by f.
$(Y, Z, U)$
and pulled back by f.
Recall that the excision sequence for Chow groups may be extended using underlined Chow groups. Imitating the definition of Chow groups, these were defined in [Reference KreschKre99], beginning with a ‘naive’ variant
![]() $\underline {A}^{\circ }_d(X)$
in [Reference KreschKre99, Definition 4.1.3], which satisfies functoriality under proper pushforwards and flat pullbacks. As before, the theory is extended via limits over projective morphisms
$\underline {A}^{\circ }_d(X)$
in [Reference KreschKre99, Definition 4.1.3], which satisfies functoriality under proper pushforwards and flat pullbacks. As before, the theory is extended via limits over projective morphisms
![]() $Z \to X$
and vector bundles on Z in [Reference KreschKre99, Corollary 4.1.10]. Here we define their restricted analogues.
$Z \to X$
and vector bundles on Z in [Reference KreschKre99, Corollary 4.1.10]. Here we define their restricted analogues.
Definition B.9. Let
![]() $f : X \to Y$
be a morphism of algebraic stacks. Let
$f : X \to Y$
be a morphism of algebraic stacks. Let
 $$\begin{align*}\underline{A}^f_d (X) = \varinjlim_{Y' \in \mathfrak{A}_{Y}} \left[ \underline{\widehat{A}}_d^{f'} \left( X' \right) / \underline{\widehat{B}}_d^{f'} \left( X' \right) \right], \end{align*}$$
$$\begin{align*}\underline{A}^f_d (X) = \varinjlim_{Y' \in \mathfrak{A}_{Y}} \left[ \underline{\widehat{A}}_d^{f'} \left( X' \right) / \underline{\widehat{B}}_d^{f'} \left( X' \right) \right], \end{align*}$$
where
![]() $\underline {\widehat {A}}_d^{f'}$
is defined in analogy with equation (41). The quotient group
$\underline {\widehat {A}}_d^{f'}$
is defined in analogy with equation (41). The quotient group
 $$\begin{align*}\underline{\widehat{B}}_d^{f'}X' = \coprod_{\begin{subarray}{c} p_1, p_2 : W \to Y' \\ g \circ p_1 \cong g \circ p_2 \end{subarray}} \coprod_{E,F \in \mathfrak{B}_{Y'}} \underline{Z}_{E, F}^f, \end{align*}$$
$$\begin{align*}\underline{\widehat{B}}_d^{f'}X' = \coprod_{\begin{subarray}{c} p_1, p_2 : W \to Y' \\ g \circ p_1 \cong g \circ p_2 \end{subarray}} \coprod_{E,F \in \mathfrak{B}_{Y'}} \underline{Z}_{E, F}^f, \end{align*}$$
where
 $$\begin{align*}\underline{Z}_{E, F}^f = \left\{p_{2*}' \beta_2 - p_{1*}' \beta_1 \left| \begin{array}{c} \beta_1 \in \underline{A}^{\circ}_{d + \mathrm{rk}\, E}({p'}_1^{*}{f'}^{*}E), \,\beta_2 \in \underline{A}^{\circ}_{d + \mathrm{rk}\, F}({p'}_2^{*}{f'}^{*}F) \\ \beta_1 \sim \beta_2 \textrm{ in } \widehat{\underline{A}}_d^{f''}(W') \end{array} \right. \right\}, \end{align*}$$
$$\begin{align*}\underline{Z}_{E, F}^f = \left\{p_{2*}' \beta_2 - p_{1*}' \beta_1 \left| \begin{array}{c} \beta_1 \in \underline{A}^{\circ}_{d + \mathrm{rk}\, E}({p'}_1^{*}{f'}^{*}E), \,\beta_2 \in \underline{A}^{\circ}_{d + \mathrm{rk}\, F}({p'}_2^{*}{f'}^{*}F) \\ \beta_1 \sim \beta_2 \textrm{ in } \widehat{\underline{A}}_d^{f''}(W') \end{array} \right. \right\}, \end{align*}$$
depends on the diagram used in the Definition B.1. There is a natural homomorphism
![]() $\iota _f: \underline {A}^f_d(X) \to \underline {A}_d(X)$
.
$\iota _f: \underline {A}^f_d(X) \to \underline {A}_d(X)$
.
Proposition B.10. Let
![]() $p : E \to Y$
be a vector bundle on a Deligne-Mumford stack. Then the natural flat pullback map
$p : E \to Y$
be a vector bundle on a Deligne-Mumford stack. Then the natural flat pullback map
![]() $p^* : \underline {A}_d^{\circ }(Y, \mathbb {Q}) \to \underline {A}_{d + \mathrm {rk}\, E}^{\circ }(E, \mathbb {Q})$
is a surjection for all d.
$p^* : \underline {A}_d^{\circ }(Y, \mathbb {Q}) \to \underline {A}_{d + \mathrm {rk}\, E}^{\circ }(E, \mathbb {Q})$
is a surjection for all d.
Proof. First, we note that the existence of the map
![]() $p^*$
follows directly from the definition of
$p^*$
follows directly from the definition of
![]() $\underline {A}_d^{\circ }$
, as was observed in [Reference KreschKre99, Remark 4.1.4]. To show that it is surjective, we first reduce to the case of global quotient stacks of the form
$\underline {A}_d^{\circ }$
, as was observed in [Reference KreschKre99, Remark 4.1.4]. To show that it is surjective, we first reduce to the case of global quotient stacks of the form
![]() $[W/G]$
for a scheme W and a finite group G. Assuming the proposition holds for such quotient stacks, let
$[W/G]$
for a scheme W and a finite group G. Assuming the proposition holds for such quotient stacks, let
![]() $U \subset Y$
be such a stack, non-empty and open in Y. Such U always exists by [Reference Laumon and Moret-BaillyLMB00, Corollaire 6.1.1]. By naturality of the long exact sequence in [Reference KreschKre99, equation (4.2.1)], there are morphisms
$U \subset Y$
be such a stack, non-empty and open in Y. Such U always exists by [Reference Laumon and Moret-BaillyLMB00, Corollaire 6.1.1]. By naturality of the long exact sequence in [Reference KreschKre99, equation (4.2.1)], there are morphisms

where
![]() $Z = Y \setminus U$
. The rightmost morphism is an isomorphism by homotopy invariance of Deligne-Mumford stacks with rational coefficients. By noetherian induction on Y, the leftmost vertical morphism is surjective. Hence
$Z = Y \setminus U$
. The rightmost morphism is an isomorphism by homotopy invariance of Deligne-Mumford stacks with rational coefficients. By noetherian induction on Y, the leftmost vertical morphism is surjective. Hence
![]() $\underline {A}_*^{\circ }(Y,\mathbb {Q}) \to \underline {A}_*^{\circ }(E, \mathbb {Q})$
is a surjection by the four lemma.
$\underline {A}_*^{\circ }(Y,\mathbb {Q}) \to \underline {A}_*^{\circ }(E, \mathbb {Q})$
is a surjection by the four lemma.
For the base case, consider a quotient
![]() $[W / G]$
with vector bundle E. Then E has the form
$[W / G]$
with vector bundle E. Then E has the form
![]() $[V / G]$
for a vector bundle
$[V / G]$
for a vector bundle
![]() $V \to W$
. There is a diagram
$V \to W$
. There is a diagram

The upper square vertical isomorphisms follow from the natural isomorphism for schemes
![]() $\underline {A}_*^{\circ }(-) {\stackrel {\sim }{\longrightarrow }} \mathrm {CH}_*(-;1)$
; see [Reference KreschKre99, Proposition 4.1.7]. The lower squares exist because the quotient morphisms are flat and proper, and they commute by compatibility of pullback and pushforward. The morphism
$\underline {A}_*^{\circ }(-) {\stackrel {\sim }{\longrightarrow }} \mathrm {CH}_*(-;1)$
; see [Reference KreschKre99, Proposition 4.1.7]. The lower squares exist because the quotient morphisms are flat and proper, and they commute by compatibility of pullback and pushforward. The morphism
![]() $r_*$
is surjective, because
$r_*$
is surjective, because
![]() $r_* \circ r^*$
is multiplication by
$r_* \circ r^*$
is multiplication by
![]() $|G|$
. But
$|G|$
. But
![]() $r_* = p^* \circ q_* \circ (s^*)^{-1}$
, so
$r_* = p^* \circ q_* \circ (s^*)^{-1}$
, so
![]() $p^*$
must also be surjective. By similar reasoning,
$p^*$
must also be surjective. By similar reasoning,
![]() $p^*$
is injective, hence an isomorphism.
$p^*$
is injective, hence an isomorphism.
Using Proposition B.10, we can generalize Lemma B.5 to the setting of underlined Chow groups.
Lemma B.11. Let
![]() $f: X \to Y$
be a representable (respectively, relative Deligne-Mumford type) morphism and let F be the pullback by f of an approximating vector bundle on Y in codimension D. Let furthermore
$f: X \to Y$
be a representable (respectively, relative Deligne-Mumford type) morphism and let F be the pullback by f of an approximating vector bundle on Y in codimension D. Let furthermore
![]() $(g, \alpha )$
be a cycle in
$(g, \alpha )$
be a cycle in
![]() $\underline {A}_d(X)$
or
$\underline {A}_d(X)$
or
![]() $\underline {A}^f_d(X)$
(respectively, a cycle in
$\underline {A}^f_d(X)$
(respectively, a cycle in
![]() $\underline {A}_d(X, \mathbb {Q})$
). When D is sufficiently large, we have
$\underline {A}_d(X, \mathbb {Q})$
). When D is sufficiently large, we have
![]() $(g, \alpha ) \sim (1_X, \delta )$
for some naive cycle
$(g, \alpha ) \sim (1_X, \delta )$
for some naive cycle
![]() $\delta \in \underline {A}^{\circ }_{d + \mathrm {rk}\, F}(F)$
(respectively,
$\delta \in \underline {A}^{\circ }_{d + \mathrm {rk}\, F}(F)$
(respectively,
![]() $\delta \in \underline {A}^{\circ }_{d + \mathrm {rk}\, F}(F, \mathbb {Q})$
). In fact, in this case the natural maps
$\delta \in \underline {A}^{\circ }_{d + \mathrm {rk}\, F}(F, \mathbb {Q})$
). In fact, in this case the natural maps
are isomorphisms.
Proof. To show the lemma, one repeats the proof of Lemma B.5 verbatim, replacing (naive) Chow groups with (naive) underlined Chow groups. In the last step of the argument, we need to show that the pullback
![]() $q^*$
under a vector bundle map
$q^*$
under a vector bundle map
![]() $q: E \oplus H \to H$
induces an isomorphism of naive underlined Chow groups in the correct degree, for f representable. To see this, we note that
$q: E \oplus H \to H$
induces an isomorphism of naive underlined Chow groups in the correct degree, for f representable. To see this, we note that
![]() $E \oplus H$
and H are algebraic spaces away from a high-codimension subset, and so by the excision sequence for naive underlined Chow groups ([Reference KreschKre99, equation (4.2.1)]) these groups are unchanged by restricting to these open subspaces. Then the isomorphism follows by identifying naive and non-naive underlined Chow groups of these algebraic spaces ([Reference KreschKre99, Corollary 4.1.10]) and using that pullback by a vector bundle induces an isomorphism for the latter ([Reference KreschKre99, Proposition 4.3.1]).Footnote
19
$E \oplus H$
and H are algebraic spaces away from a high-codimension subset, and so by the excision sequence for naive underlined Chow groups ([Reference KreschKre99, equation (4.2.1)]) these groups are unchanged by restricting to these open subspaces. Then the isomorphism follows by identifying naive and non-naive underlined Chow groups of these algebraic spaces ([Reference KreschKre99, Corollary 4.1.10]) and using that pullback by a vector bundle induces an isomorphism for the latter ([Reference KreschKre99, Proposition 4.3.1]).Footnote
19
On the other hand, in case f is of relative Deligne-Mumford type, we need to show that
![]() $q^*$
gives a surjection, which follows from Proposition B.10.
$q^*$
gives a surjection, which follows from Proposition B.10.
Proposition B.12. If
![]() $f : X \to Y$
is representable and
$f : X \to Y$
is representable and
![]() $Y=[V/G]$
is the global quotient stack of a quasi-projective scheme V by a linear algebraic group G acting linearly on U, then the natural morphism
$Y=[V/G]$
is the global quotient stack of a quasi-projective scheme V by a linear algebraic group G acting linearly on U, then the natural morphism
![]() $\iota _f : \underline {A}_d^f (X) \to \underline {A}_d (X)$
is an isomorphism for all d.
$\iota _f : \underline {A}_d^f (X) \to \underline {A}_d (X)$
is an isomorphism for all d.
Proof. The assumptions on Y imply that it possesses approximating vector bundles that are algebraic spaces away from subsets of arbitrarily large codimension by using [Reference Edidin and GrahamEG98, Lemma 9, Proposition 23]. Let F be the pullback by f of such a vector bundle; then the map
![]() $\iota _f$
is simply the composition
$\iota _f$
is simply the composition
![]() $\iota _f = j \circ j_f^{-1}$
for the isomorphisms
$\iota _f = j \circ j_f^{-1}$
for the isomorphisms
![]() $j,j_f$
from equation (46).
$j,j_f$
from equation (46).
For relative Deligne-Mumford type morphisms, we have a weaker property that is enough for our purpose.
Proposition B.13. If
![]() $f : X \to Y$
is of relative Deligne-Mumford type and Y is a global quotient stack, the natural morphism
$f : X \to Y$
is of relative Deligne-Mumford type and Y is a global quotient stack, the natural morphism
![]() $\iota _f: \underline {A}^f_d(X, \mathbb {Q}) \to \underline {A}_d(X, \mathbb {Q})$
is a surjection for all d.
$\iota _f: \underline {A}^f_d(X, \mathbb {Q}) \to \underline {A}_d(X, \mathbb {Q})$
is a surjection for all d.
Proof. Let
![]() $(g, \alpha ) \in \underline {A}_d(X, \mathbb {Q})$
. By Lemma B.11,
$(g, \alpha ) \in \underline {A}_d(X, \mathbb {Q})$
. By Lemma B.11,
![]() $(g, \alpha ) \sim (1_X, \delta )$
for some naive cycle
$(g, \alpha ) \sim (1_X, \delta )$
for some naive cycle
![]() $\delta $
on the pullback of a vector bundle on Y by f. Then
$\delta $
on the pullback of a vector bundle on Y by f. Then
![]() $(1_X, \delta )$
maps to
$(1_X, \delta )$
maps to
![]() $(g, \alpha )$
under
$(g, \alpha )$
under
![]() $\iota _f$
.
$\iota _f$
.
Proposition B.14. With the notation of Proposition B.8, there is a connecting homomorphism
![]() $\delta _f$
fitting into a commutative diagram with the connecting homomorphism of [Reference KreschKre99, equation (4.2.2)],
$\delta _f$
fitting into a commutative diagram with the connecting homomorphism of [Reference KreschKre99, equation (4.2.2)],

Proof. The construction of
![]() $\delta $
in [Reference KreschKre99, equation (4.2.2)] goes through for restricted Chow groups.
$\delta $
in [Reference KreschKre99, equation (4.2.2)] goes through for restricted Chow groups.
Propositions B.8 and B.14 fit together in an exact sequence.
Proposition B.15. With the notation of Proposition B.8, let U be a global quotient stack. Then there is an exact sequence
Proof. The proof is completely analogous to the proof of [Reference KreschKre99, Proposition 4.2.1].
B.3 Main theorems
Recall that a stack admits a stratification by global quotient stacks if and only if every geometric stabilizer is affine [Reference KreschKre99, Proposition 3.5.9].
Proposition B.16. Let Y be a stack stratified by global quotient stacks, and let
![]() $f : X \to Y$
be representable. Then
$f : X \to Y$
be representable. Then
![]() $\mathrm {CH}^f_d(X) \to \mathrm {CH}_d(X)$
is an isomorphism for all d. If, alternatively, f is of relative Deligne-Mumford type, then
$\mathrm {CH}^f_d(X) \to \mathrm {CH}_d(X)$
is an isomorphism for all d. If, alternatively, f is of relative Deligne-Mumford type, then
![]() $\mathrm {CH}^f_d(X, \mathbb {Q}) \to \mathrm {CH}_d(X, \mathbb {Q})$
is an isomorphism for all d.
$\mathrm {CH}^f_d(X, \mathbb {Q}) \to \mathrm {CH}_d(X, \mathbb {Q})$
is an isomorphism for all d.
Proof. The proof proceeds by Noetherian induction. Using the same notation as Proposition B.8, let U be a nonempty global quotient stack. There is a morphism from the exact sequence of Proposition B.15 to the exact sequence of [Reference KreschKre99, Proposition 4.2.1]

The morphism a is an isomorphism by the induction hypothesis and morphism c by Proposition B.6. Then
![]() $c'$
is an isomorphism by Proposition B.12 if f is representable, and is a surjection by Proposition B.13 if f is of relative Deligne-Mumford type where all Chow groups are taken with
$c'$
is an isomorphism by Proposition B.12 if f is representable, and is a surjection by Proposition B.13 if f is of relative Deligne-Mumford type where all Chow groups are taken with
![]() $\mathbb {Q}$
-coefficients. By the five lemma, b is also an isomorphism.
$\mathbb {Q}$
-coefficients. By the five lemma, b is also an isomorphism.
Theorem B.17. Let Y be an algebraic stack stratified by global quotient stacks, and let
![]() $f : X \to Y$
be a proper, representable morphism. Then there is a proper pushforward
$f : X \to Y$
be a proper, representable morphism. Then there is a proper pushforward
![]() $f_* : \mathrm {CH}_d(X) \to \mathrm {CH}_d(Y)$
for all d. If, instead, f is proper and of relative Deligne-Mumford type, then there is a proper pushforward
$f_* : \mathrm {CH}_d(X) \to \mathrm {CH}_d(Y)$
for all d. If, instead, f is proper and of relative Deligne-Mumford type, then there is a proper pushforward
![]() $f_* : \mathrm {CH}_d(X, \mathbb {Q}) \to \mathrm {CH}_d(Y, \mathbb {Q})$
for all d.
$f_* : \mathrm {CH}_d(X, \mathbb {Q}) \to \mathrm {CH}_d(Y, \mathbb {Q})$
for all d.
Proof. The pushforward arises from the factorization

In case f is of relative Deligne-Mumford type, Chow groups should be taken with
![]() $\mathbb {Q}$
-coefficients.
$\mathbb {Q}$
-coefficients.
B.4 Properties of proper pushforward
The proper pushforward satisfies the following expected properties.
Proposition B.18. Let Y be an algebraic stack stratified by global quotient stacks and let
![]() $f\colon X\to Y$
be a proper, representable morphism as above. Then the proper pushforward is compatible with the representable flat pullback and refined Gysin maps for representable regular local immersions. The same compatibilities hold for Chow groups with
$f\colon X\to Y$
be a proper, representable morphism as above. Then the proper pushforward is compatible with the representable flat pullback and refined Gysin maps for representable regular local immersions. The same compatibilities hold for Chow groups with
![]() $\mathbb {Q}$
-coefficients when f is of relative Deligne-Mumford type.
$\mathbb {Q}$
-coefficients when f is of relative Deligne-Mumford type.
Proof. We will prove the case when f is a representable morphism. The proof for the Deligne-Mumford type is similar. We first prove the compatibility of proper pushforwards with flat pullbacks. Consider a Cartesian diagram

where
![]() $u\colon Z\to Y$
is a representable flat morphism of relative constant dimension
$u\colon Z\to Y$
is a representable flat morphism of relative constant dimension
![]() $\ell $
. Since u is representable, Z is stratified by global quotient stacks (see [Reference KreschKre99, Proposition 3.5.5]). By property (iii) mentioned above Proposition B.8, the natural isomorphism
$\ell $
. Since u is representable, Z is stratified by global quotient stacks (see [Reference KreschKre99, Proposition 3.5.5]). By property (iii) mentioned above Proposition B.8, the natural isomorphism
![]() $\mathrm {CH}^f_*\to \mathrm {CH}_*$
is compatible with flat pullbacks. A class
$\mathrm {CH}^f_*\to \mathrm {CH}_*$
is compatible with flat pullbacks. A class
![]() $(\rho ,\alpha )$
in
$(\rho ,\alpha )$
in
![]() $\mathrm {CH}^f_*(X)$
is represented by the following Cartesian diagram
$\mathrm {CH}^f_*(X)$
is represented by the following Cartesian diagram

where
![]() $\rho $
is a projective morphism, E is a vector bundle on
$\rho $
is a projective morphism, E is a vector bundle on
![]() $Y'$
and
$Y'$
and
![]() $\alpha $
is a class in
$\alpha $
is a class in
![]() $\mathrm {CH}^{\circ }_{d+\mathrm {rk} E'}(E')$
. By pulling back equation (48) along equation (47), we get
$\mathrm {CH}^{\circ }_{d+\mathrm {rk} E'}(E')$
. By pulling back equation (48) along equation (47), we get

where F is the pullback of E to
![]() $Z\times _Y Y'$
and
$Z\times _Y Y'$
and
![]() $F'$
is the pullback of
$F'$
is the pullback of
![]() $E'$
to
$E'$
to
![]() $W\times _X X'$
. This diagram commutes because of the corresponding statement for naive Chow groups. Therefore the following diagram
$W\times _X X'$
. This diagram commutes because of the corresponding statement for naive Chow groups. Therefore the following diagram

commutes.
The compatibility with regular local immersions states that for the Cartesian diagram in equation (47) with u a regular local immersion, we have
![]() $u^! f_* = g_* v^!$
. Note that here the pushforward by g is well-defined since the assumption that Y is stratified by global quotient stacks together with the representability of u implies that Z likewise is stratified by global quotient stacks, using [Reference KreschKre99, Proposition 3.5.5]. Then the desired compatibility also follows from a formal argument as above (see [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Proposition 18]).
$u^! f_* = g_* v^!$
. Note that here the pushforward by g is well-defined since the assumption that Y is stratified by global quotient stacks together with the representability of u implies that Z likewise is stratified by global quotient stacks, using [Reference KreschKre99, Proposition 3.5.5]. Then the desired compatibility also follows from a formal argument as above (see [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Proposition 18]).
The following proposition is a generalization of [Reference VistoliVis89, Lemma 3.8] to algebraic stacks.
Proposition B.19. Let X and Y be algebraic stacks, finite type over a field k and stratified by global quotient stacks. Let
![]() $f \colon X \to Y$
be a proper, surjective morphism of relative Deligne-Mumford type. Then the pushforward
$f \colon X \to Y$
be a proper, surjective morphism of relative Deligne-Mumford type. Then the pushforward
is surjective for all d.
Proof. By the assumption of being stratified by global quotient stacks, there exists a nonempty open substack
![]() $U \subset Y$
isomorphic to a quotient
$U \subset Y$
isomorphic to a quotient
![]() $U \cong [T / G]$
of a quasi-projective scheme T by a smooth, connected linear algebraic group G acting linearly on T. Let
$U \cong [T / G]$
of a quasi-projective scheme T by a smooth, connected linear algebraic group G acting linearly on T. Let
![]() $Z=Y \setminus U$
be the complement. Consider a commutative diagram
$Z=Y \setminus U$
be the complement. Consider a commutative diagram

with exact rows from the excision sequences and vertical arrows from the proper pushforwards by f as defined above. Commutativity of the squares follows from the compatibility of proper pushforwards with compositions of proper maps and pullbacks by flat maps. The pushforward
![]() $f_*$
is surjective over Y if it is surjective over U and Z by the four lemma. Since the assumptions of the proposition hold for Z and since Y is of finite type, we can reduce by Noetherian induction to showing the statement over U.
$f_*$
is surjective over Y if it is surjective over U and Z by the four lemma. Since the assumptions of the proposition hold for Z and since Y is of finite type, we can reduce by Noetherian induction to showing the statement over U.
By [Reference KreschKre99, Proposition 3.5.10], the global quotient U admits a vector bundle
![]() $\pi : E \to U$
such that E is represented by a scheme off a locus of arbitrarily high codimension. Moreover, the pullback
$\pi : E \to U$
such that E is represented by a scheme off a locus of arbitrarily high codimension. Moreover, the pullback
![]() $\pi ^*$
induces an isomorphism of Chow groups. Let
$\pi ^*$
induces an isomorphism of Chow groups. Let
![]() $V=f^{-1}(U)$
and
$V=f^{-1}(U)$
and
![]() $E' = (f|_{V})^* E \to V$
be the pullback of E under f. It suffices to show that the pushforward under
$E' = (f|_{V})^* E \to V$
be the pullback of E under f. It suffices to show that the pushforward under
![]() $E' \to E$
is surjective because of the compatibility of proper pushforward with flat pullback. This computation can be done away from the locus where E is not a scheme because we work in a fixed dimension d. Thus we have reduced to the case where the target is a scheme.
$E' \to E$
is surjective because of the compatibility of proper pushforward with flat pullback. This computation can be done away from the locus where E is not a scheme because we work in a fixed dimension d. Thus we have reduced to the case where the target is a scheme.
Now assume that
![]() $f:X \to Y$
is as in the proposition and Y is a scheme. Then the domain is a Deligne-Mumford stack because f is assumed to be of relative Deligne-Mumford type. By [Reference Edidin, Hassett, Kresch and VistoliEHKV01, Theorem 2.7], such a stack admits a finite surjective morphism from a scheme. This means the machinery of Chow groups as developed by Vistoli in [Reference VistoliVis89] is applicable. By [Reference VistoliVis89, Lemma 3.8], the pushforward
$f:X \to Y$
is as in the proposition and Y is a scheme. Then the domain is a Deligne-Mumford stack because f is assumed to be of relative Deligne-Mumford type. By [Reference Edidin, Hassett, Kresch and VistoliEHKV01, Theorem 2.7], such a stack admits a finite surjective morphism from a scheme. This means the machinery of Chow groups as developed by Vistoli in [Reference VistoliVis89] is applicable. By [Reference VistoliVis89, Lemma 3.8], the pushforward
![]() $f_*$
is surjective on naive Chow groups (with
$f_*$
is surjective on naive Chow groups (with
![]() $\mathbb {Q}$
-coefficients). Since Y is a scheme, the naive Chow groups agree with those defined in [Reference KreschKre99], so for every cycle on Y, there exists a naive cycle on X pushing forward to it. Finally, for naive cycles on X, the definition of proper pushforward agrees with the naive pushforward, so we are done.
$\mathbb {Q}$
-coefficients). Since Y is a scheme, the naive Chow groups agree with those defined in [Reference KreschKre99], so for every cycle on Y, there exists a naive cycle on X pushing forward to it. Finally, for naive cycles on X, the definition of proper pushforward agrees with the naive pushforward, so we are done.
Remark B.20. Even in very good situations, the pushforward by proper, surjective maps of finite type stacks is not surjective on naive Chow groups. Indeed, for
![]() $n \geq 1$
, consider the map
$n \geq 1$
, consider the map
where
![]() $\mathrm {PGL}_{n+1}$
acts in the usual way on
$\mathrm {PGL}_{n+1}$
acts in the usual way on
![]() $\mathbb {P}^n$
. Then f is a representable, proper surjective morphism of quotient stacks, and in fact we claim that it is also projective. To see the latter, note that the line bundle
$\mathbb {P}^n$
. Then f is a representable, proper surjective morphism of quotient stacks, and in fact we claim that it is also projective. To see the latter, note that the line bundle
![]() $\mathcal {O}_{\mathbb {P}^n}(n+1)$
on
$\mathcal {O}_{\mathbb {P}^n}(n+1)$
on
![]() $\mathbb {P}^n$
is
$\mathbb {P}^n$
is
![]() $\mathrm {PGL}_{n+1}$
-linearisable (see, e.g., [Reference BrionBri18, Example 3.2.7]). Thus it descends to a line bundle on
$\mathrm {PGL}_{n+1}$
-linearisable (see, e.g., [Reference BrionBri18, Example 3.2.7]). Thus it descends to a line bundle on
![]() $[\mathbb {P}^n / \mathrm {PGL}_{n+1}]$
, which is relatively ample for f. Therefore, the proper morphism f is indeed projective. However, even though f has all these nice properties, the pushforward
$[\mathbb {P}^n / \mathrm {PGL}_{n+1}]$
, which is relatively ample for f. Therefore, the proper morphism f is indeed projective. However, even though f has all these nice properties, the pushforward
![]() $f_*$
still vanishes on naive Chow groups. Let
$f_*$
still vanishes on naive Chow groups. Let
![]() $V\to [\mathbb {P}^n/\mathrm {PGL}_{n+1}]$
be an integral closed substack. Let
$V\to [\mathbb {P}^n/\mathrm {PGL}_{n+1}]$
be an integral closed substack. Let
![]() $V_{\mathbb {P}^n}$
be the fibre product
$V_{\mathbb {P}^n}$
be the fibre product

Then
![]() $V_{\mathbb {P}^n}$
is a closed subscheme of
$V_{\mathbb {P}^n}$
is a closed subscheme of
![]() $\mathbb {P}^n$
that is invariant under
$\mathbb {P}^n$
that is invariant under
![]() $\mathrm {PGL}_{n+1}$
so
$\mathrm {PGL}_{n+1}$
so
![]() $V_{\mathbb {P}^n} = \mathbb {P}^n$
and thus also
$V_{\mathbb {P}^n} = \mathbb {P}^n$
and thus also
![]() $V=[\mathbb {P}^n/\mathrm {PGL}_{n+1}]$
. On the other hand, f is relative dimension n, hence
$V=[\mathbb {P}^n/\mathrm {PGL}_{n+1}]$
. On the other hand, f is relative dimension n, hence
![]() $f_*[V]$
=0. We are grateful to Andrew Kresch, who pointed out this example to us.
$f_*[V]$
=0. We are grateful to Andrew Kresch, who pointed out this example to us.
Remark B.21. Since the proper pushforward constructed in this section is compatible with flat pullbacks, it follows immediately from the definition of Chow groups of locally finite type stacks in the previous section that these inherit the proper pushforward construction. In particular, Theorem B.17 and Proposition B.18 remain true for stacks only locally of finite type.
On the other hand, Proposition B.19 remains true for algebraic stacks
![]() $X,Y$
that are Lindelöf and stratified by global quotient stacks (as is the case for the stacks
$X,Y$
that are Lindelöf and stratified by global quotient stacks (as is the case for the stacks
![]() $\mathfrak {M}_{g,n,a}$
described in Section 2.2).
$\mathfrak {M}_{g,n,a}$
described in Section 2.2).
Indeed, let
![]() $U_i$
be a finite type cover of Y; then
$U_i$
be a finite type cover of Y; then
![]() $V_i = f^{-1}(U_i)$
is also finite type since f is proper. Let
$V_i = f^{-1}(U_i)$
is also finite type since f is proper. Let
![]() $K_i$
be the kernel of the proper pushforward
$K_i$
be the kernel of the proper pushforward
![]() $f_*: \mathrm {CH}_*(V_i) \to \mathrm {CH}_*(U_i)$
; then applying the proposition, we have a commutative diagram
$f_*: \mathrm {CH}_*(V_i) \to \mathrm {CH}_*(U_i)$
; then applying the proposition, we have a commutative diagram

The columns are exact by Proposition B.19, and the middle and the bottom rows are exact by [Reference KreschKre99, Proposition 2.3.6]. Applying a small variant of the Snake lemma,Footnote
20
we see that the maps
![]() $K_i \to K_j$
of the directed system
$K_i \to K_j$
of the directed system
![]() $(K_i)_i$
are surjective, so this system is Mittag-Leffler (see [Sta20, Tag 0596]). Then it follows from [Sta20, Tag 0598] that the induced map
$(K_i)_i$
are surjective, so this system is Mittag-Leffler (see [Sta20, Tag 0596]). Then it follows from [Sta20, Tag 0598] that the induced map
is indeed surjective.
C Operational Chow groups for algebraic stacks
In this section, we give a definition of operational Chow classes for algebraic stacks, which we assume throughout to be locally finite type over k.
Definition C.1. An operational class c in the pth operational Chow group
![]() $\mathrm {CH}_{\mathrm {OP}}^p(X)$
is a collection of homomorphisms
$\mathrm {CH}_{\mathrm {OP}}^p(X)$
is a collection of homomorphisms
for all morphisms
![]() $g\colon B\to X$
, where B is an algebraic stack of finite type over k, stratified by global quotient stacks and for all integers m, compatible with representable proper pushforward, flat pullback, and refined Gysin pullback along representable lci morphisms (see [Reference FultonFul98, Section 17.1]). In particular, the compatibility with refined Gysin pullback means the following compatibility condition: consider a diagram
$g\colon B\to X$
, where B is an algebraic stack of finite type over k, stratified by global quotient stacks and for all integers m, compatible with representable proper pushforward, flat pullback, and refined Gysin pullback along representable lci morphisms (see [Reference FultonFul98, Section 17.1]). In particular, the compatibility with refined Gysin pullback means the following compatibility condition: consider a diagram

where
![]() $g : B \to X$
is a morphism from an algebraic stack B of finite type over k, stratified by global quotient stacks,
$g : B \to X$
is a morphism from an algebraic stack B of finite type over k, stratified by global quotient stacks,
![]() $f: Z' \to Z$
is a representable lci morphism and
$f: Z' \to Z$
is a representable lci morphism and
![]() $Z'$
is stratified by global quotient stacks and the square in the diagram is Cartesian. Then we require that for all
$Z'$
is stratified by global quotient stacks and the square in the diagram is Cartesian. Then we require that for all
![]() $c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
and
$c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
and
![]() $\alpha \in \mathrm {CH}_*(B)$
, we have
$\alpha \in \mathrm {CH}_*(B)$
, we have
This notion of the operational Chow group of algebraic stacks shares the following formal properties of the operational Chow group of schemes: it is a contravariant functor for all morphisms and has the structure of an associative
![]() $\mathbb {Q}$
-algebra coming from composing two operations. Note that for the functoriality under all morphisms, it is important that we did not restrict the morphisms
$\mathbb {Q}$
-algebra coming from composing two operations. Note that for the functoriality under all morphisms, it is important that we did not restrict the morphisms
![]() $g : B \to X$
in the definition above, for example, to be representable. Otherwise, we would only get functoriality under representable morphisms.
$g : B \to X$
in the definition above, for example, to be representable. Otherwise, we would only get functoriality under representable morphisms.
Example C.2. Let E be a vector bundle on X; then its rth Chern class
is naturally an operational class on X. Given
![]() $g: B \to X$
, it acts by
$g: B \to X$
, it acts by
where the Chern class of
![]() $g^* E$
and its action on the cycle
$g^* E$
and its action on the cycle
![]() $\alpha $
on B are as defined in [Reference KreschKre99].
$\alpha $
on B are as defined in [Reference KreschKre99].
We start with a small observation: the operational Chow group of X can be computed on a suitable finite-type cover of X.
Lemma C.3. Let X be a locally finite type algebraic stack over k. Let
![]() $(\mathcal {U}_i)_{i \in I}$
be a directed system of finite type open substacks of X whose union is all of X. Then the flat pullbacks
$(\mathcal {U}_i)_{i \in I}$
be a directed system of finite type open substacks of X whose union is all of X. Then the flat pullbacks
![]() $j_i^*$
by the inclusions
$j_i^*$
by the inclusions
![]() $j_i : \mathcal {U}_i \to X$
induce a map
$j_i : \mathcal {U}_i \to X$
induce a map
and this map
![]() $\Phi $
is an isomorphism.
$\Phi $
is an isomorphism.
Proof. The proof, which uses the fact that each map
![]() $B \to X$
from a finite-type stack B must factor through one of the
$B \to X$
from a finite-type stack B must factor through one of the
![]() $\mathcal U_i$
by Noetherian induction, goes verbatim as the proof presented in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Corollary 15].
$\mathcal U_i$
by Noetherian induction, goes verbatim as the proof presented in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Corollary 15].
Lemma C.4. Let
![]() $f\colon X\to Y$
be a representable, proper, flat morphism of relative dimension d. Then there is a pushforward map
$f\colon X\to Y$
be a representable, proper, flat morphism of relative dimension d. Then there is a pushforward map
defined as follows. For a Cartesian diagram

and
![]() $c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
,
$c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
,
If
![]() $f\colon X\to Y$
is a representable, proper, lci morphism of relative dimension d, the pushforward map is similarly defined by the formula
$f\colon X\to Y$
is a representable, proper, lci morphism of relative dimension d, the pushforward map is similarly defined by the formula
using the refined Gysin pullback. For a morphism f that is representable, flat and lci, the two definitions coincide.
Proof. We check that the collection of maps
![]() $f_*c$
defines an operational Chow class. We will only give a proof for the case that f is lci; the proof for flat morphisms is similar. The fact that the two notions coincide for f both flat and lci follows from the formula and the fact that the flat pullback and the lci pullback of cycles coincide.
$f_*c$
defines an operational Chow class. We will only give a proof for the case that f is lci; the proof for flat morphisms is similar. The fact that the two notions coincide for f both flat and lci follows from the formula and the fact that the flat pullback and the lci pullback of cycles coincide.
Let
![]() $h\colon B'\to B$
be a representable proper morphism, and consider the following Cartesian diagram:
$h\colon B'\to B$
be a representable proper morphism, and consider the following Cartesian diagram:

For
![]() $c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
and
$c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
and
![]() $\alpha \in \mathrm {CH}_*(B')$
, we have
$\alpha \in \mathrm {CH}_*(B')$
, we have
 $$ \begin{align*} h_* (f_* c)(g \circ h)(\alpha) &= h_* \left( f^{\prime\prime}_*( c(g' \circ h') \cdot f^! \alpha)\right) \\ &= f^{\prime}_* \left( h^{\prime}_*( c(g' \circ h') \cdot f^! \alpha)\right) \\ &= f^{\prime}_* \left( c(g' ) \cdot h^{\prime}_* f^! \alpha\right) \\ &= f^{\prime}_* \left( c(g' ) \cdot f^! h_* \alpha\right) = (f_* c)(g)(h_* \alpha), \end{align*} $$
$$ \begin{align*} h_* (f_* c)(g \circ h)(\alpha) &= h_* \left( f^{\prime\prime}_*( c(g' \circ h') \cdot f^! \alpha)\right) \\ &= f^{\prime}_* \left( h^{\prime}_*( c(g' \circ h') \cdot f^! \alpha)\right) \\ &= f^{\prime}_* \left( c(g' ) \cdot h^{\prime}_* f^! \alpha\right) \\ &= f^{\prime}_* \left( c(g' ) \cdot f^! h_* \alpha\right) = (f_* c)(g)(h_* \alpha), \end{align*} $$
where the third equality uses the compatibility with proper pushforward for the operational class c and the fourth equality uses compatibility of Gysin pullback and proper pushforward in Proposition B.18.
Similarly, let
![]() $h\colon B'\to B$
be a flat morphism and
$h\colon B'\to B$
be a flat morphism and
![]() $\beta \in \mathrm {CH}_*(B)$
; then we have
$\beta \in \mathrm {CH}_*(B)$
; then we have
 $$ \begin{align*} (f_* c)(g \circ h)(h^* \beta) &= f^{\prime\prime}_*( c(g' \circ h') \cdot f^! h^* \beta) \\ &= f^{\prime\prime}_*( c(g' \circ h') \cdot (h')^* f^! \beta) \\ &= f^{\prime\prime}_*( (h')^* ( c(g') \cdot f^! \beta) )\\ &= h^* f^{\prime}_* ( c(g') \cdot f^! \beta) = h^*(f_* c)(g )(\beta), \end{align*} $$
$$ \begin{align*} (f_* c)(g \circ h)(h^* \beta) &= f^{\prime\prime}_*( c(g' \circ h') \cdot f^! h^* \beta) \\ &= f^{\prime\prime}_*( c(g' \circ h') \cdot (h')^* f^! \beta) \\ &= f^{\prime\prime}_*( (h')^* ( c(g') \cdot f^! \beta) )\\ &= h^* f^{\prime}_* ( c(g') \cdot f^! \beta) = h^*(f_* c)(g )(\beta), \end{align*} $$
where the second equality uses compatibility of Gysin maps with flat pullbacks, the third equality uses that c is compatible with flat pullbacks and the fourth equality uses that pushforwards are compatible with flat pullbacks.
Let
![]() $j\colon B\to Z$
be a morphism and
$j\colon B\to Z$
be a morphism and
![]() $h\colon Z'\to Z$
be a (representable) regular local immersion where
$h\colon Z'\to Z$
be a (representable) regular local immersion where
![]() $Z'$
is stratified by global quotient stacks. Consider the fibre diagram
$Z'$
is stratified by global quotient stacks. Consider the fibre diagram

For
![]() $\alpha \in \mathrm {CH}_*(B)$
, we have
$\alpha \in \mathrm {CH}_*(B)$
, we have
 $$ \begin{align*} h^!(f_*c)(g)(\alpha) &= h^!\left(f^{\prime}_*(c(g')\cdot f^!\alpha)\right)\\ &=f^{\prime\prime}_*\left(h^!(c(g')\cdot f^!\alpha)\right)\\ &=f^{\prime\prime}_*\left(c(g'\circ h'')\cdot h^!f^!(\alpha)\right)\\ &=f^{\prime\prime}_*\left(c(g'\circ h'')\cdot f^!h^!(\alpha)\right)=(f_*c)(g\circ h')(h^!\alpha), \end{align*} $$
$$ \begin{align*} h^!(f_*c)(g)(\alpha) &= h^!\left(f^{\prime}_*(c(g')\cdot f^!\alpha)\right)\\ &=f^{\prime\prime}_*\left(h^!(c(g')\cdot f^!\alpha)\right)\\ &=f^{\prime\prime}_*\left(c(g'\circ h'')\cdot h^!f^!(\alpha)\right)\\ &=f^{\prime\prime}_*\left(c(g'\circ h'')\cdot f^!h^!(\alpha)\right)=(f_*c)(g\circ h')(h^!\alpha), \end{align*} $$
where the fourth equality comes from the commutativity of refined Gysin pullback ([Reference KreschKre99, Section 3.1]) and the second equality comes from Proposition B.18.
Lemma C.5. Let X be an equidimensional algebraic stack of dimension n that is stratified by global quotient stacks. Then there exists a well-defined map
Proof. Let
![]() $(\mathcal {U}_i)_{i \in I}$
be a directed system of finite type open substacks of X whose union is all of X. Given
$(\mathcal {U}_i)_{i \in I}$
be a directed system of finite type open substacks of X whose union is all of X. Given
![]() $c \in \mathrm {CH}_{\mathrm {OP}}^*(X)$
, for each open embedding
$c \in \mathrm {CH}_{\mathrm {OP}}^*(X)$
, for each open embedding
![]() $\iota _i\colon \mathcal {U}_i\to X$
, we consider the cycle
$\iota _i\colon \mathcal {U}_i\to X$
, we consider the cycle
![]() $c(\iota _i)\cdot [\mathcal {U}_i] \in \mathrm {CH}_*(\mathcal {U}_i)$
. For a given
$c(\iota _i)\cdot [\mathcal {U}_i] \in \mathrm {CH}_*(\mathcal {U}_i)$
. For a given
![]() $i\in I$
, let
$i\in I$
, let
![]() $\ell \in I$
be an element such that
$\ell \in I$
be an element such that
![]() $\mathcal {U}_{\ell }$
contains
$\mathcal {U}_{\ell }$
contains
![]() $\mathcal {U}_i$
. Let
$\mathcal {U}_i$
. Let
![]() $\iota _{i\ell }:\mathcal {U}_i\to \mathcal {U}_{\ell }$
be the open embedding. Since an operational Chow class commutes with the flat pullback, we have
$\iota _{i\ell }:\mathcal {U}_i\to \mathcal {U}_{\ell }$
be the open embedding. Since an operational Chow class commutes with the flat pullback, we have
Therefore the collection of cycles
![]() $c(\iota _i)\cdot [\mathcal {U}_i]$
gives a well-defined element in
$c(\iota _i)\cdot [\mathcal {U}_i]$
gives a well-defined element in
![]() $\varprojlim _{i \in I} \mathrm {CH}_*(\mathcal U_i)$
.
$\varprojlim _{i \in I} \mathrm {CH}_*(\mathcal U_i)$
.
The following theorem is an analogy of the Poincaré duality for smooth stacks.
Theorem C.6. Let X be a smooth equidimensional algebraic stack of dimension n stratified by global quotient stacks. Then the canonical map in equation (53) with
![]() $\mathbb {Q}$
-coefficients is an isomorphism of associative
$\mathbb {Q}$
-coefficients is an isomorphism of associative
![]() $\mathbb {Q}$
-algebras.
$\mathbb {Q}$
-algebras.
Proof. In the following proof, all Chow groups are with
![]() $\mathbb {Q}$
-coefficients. By Lemma C.3, we see that both sides of equation (53) can be defined as the inverse limit over a cover of X by finite-type open substacks
$\mathbb {Q}$
-coefficients. By Lemma C.3, we see that both sides of equation (53) can be defined as the inverse limit over a cover of X by finite-type open substacks
![]() $\mathcal {U}_i$
and the map in equation (53) is the map induced by the compatible system of maps
$\mathcal {U}_i$
and the map in equation (53) is the map induced by the compatible system of maps
Thus it suffices to prove the result for X of finite type over k.
To start, there exists a map
constructed in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Section 2.3]. Given
![]() $\beta \in \mathrm {CH}_{n-*}(X)$
and
$\beta \in \mathrm {CH}_{n-*}(X)$
and
![]() $\varphi : B \to X$
from an algebraic stack finite type over k, stratified by global quotient stacks, consider the graph morphism
$\varphi : B \to X$
from an algebraic stack finite type over k, stratified by global quotient stacks, consider the graph morphism
![]() $\varphi _B : B \to B \times X$
. Then
$\varphi _B : B \to B \times X$
. Then
![]() $\varphi _B$
is representable and regular local immersion because X is smooth over k. The map
$\varphi _B$
is representable and regular local immersion because X is smooth over k. The map
![]() $\Phi $
is defined by
$\Phi $
is defined by
We show that
![]() $\Phi $
is the inverse of
$\Phi $
is the inverse of
![]() $\cap \,[X]$
following the parallel argument in [Reference FultonFul98, Chapter 17]. We note that from the definition of
$\cap \,[X]$
following the parallel argument in [Reference FultonFul98, Chapter 17]. We note that from the definition of
![]() $\Phi $
it is easy to see that it is multiplicative, using that the product in
$\Phi $
it is easy to see that it is multiplicative, using that the product in
![]() $\mathrm {CH}_*(X)$
is defined by
$\mathrm {CH}_*(X)$
is defined by
![]() $\beta _1 \cdot \beta _2 = \Delta ^! ( \beta _1 \times \beta _2)$
, where
$\beta _1 \cdot \beta _2 = \Delta ^! ( \beta _1 \times \beta _2)$
, where
![]() $\Delta \colon X\to X\times X$
is the diagonal morphism.
$\Delta \colon X\to X\times X$
is the diagonal morphism.
Let
![]() $p_2\colon X\times X\to X$
be the projection to the second factor. For all
$p_2\colon X\times X\to X$
be the projection to the second factor. For all
![]() $\beta \in \mathrm {CH}_*(X)$
, we have
$\beta \in \mathrm {CH}_*(X)$
, we have
by the functoriality of the Gysin pullback. It shows that
![]() $\Phi (\beta )\cap [X]=\beta $
.
$\Phi (\beta )\cap [X]=\beta $
.
We prove the other direction. For
![]() $c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
and
$c\in \mathrm {CH}_{\mathrm {OP}}^*(X)$
and
![]() $\alpha \in \mathrm {CH}_*(B)$
it is sufficient to prove that
$\alpha \in \mathrm {CH}_*(B)$
it is sufficient to prove that
Let
![]() $p_2 \colon B\times X\to X$
be the projection to the second factor. We first prove
$p_2 \colon B\times X\to X$
be the projection to the second factor. We first prove
When B is equidimensional and
![]() $\alpha $
is the class of the fundamental class
$\alpha $
is the class of the fundamental class
![]() $[B]$
, the equality follows from the compatibility of c with flat pullback by
$[B]$
, the equality follows from the compatibility of c with flat pullback by
![]() $p_2$
:
$p_2$
:
A general class
![]() $\alpha $
can be represented as
$\alpha $
can be represented as
![]() $(f,\alpha _0)$
, where
$(f,\alpha _0)$
, where
![]() $f\colon Y\to B$
is a projective morphism and E is a vector bundle on Y and
$f\colon Y\to B$
is a projective morphism and E is a vector bundle on Y and
![]() $\alpha _0\in \mathrm {CH}^{\circ }_*(E)$
. Adding a trivial component to Y, we may assume f is surjective. By Proposition B.19 and the homotopy invariance property, it is enough to check this equality for a class in
$\alpha _0\in \mathrm {CH}^{\circ }_*(E)$
. Adding a trivial component to Y, we may assume f is surjective. By Proposition B.19 and the homotopy invariance property, it is enough to check this equality for a class in
![]() $\mathrm {CH}^{\circ }_*(E)$
. A class in
$\mathrm {CH}^{\circ }_*(E)$
. A class in
![]() $\mathrm {CH}^{\circ }_*(E)$
can be written as a linear combination of classes
$\mathrm {CH}^{\circ }_*(E)$
can be written as a linear combination of classes
![]() $[V]$
, where
$[V]$
, where
![]() $j:V\to E$
are integral closed substacks. Thus it suffices to show the statement for
$j:V\to E$
are integral closed substacks. Thus it suffices to show the statement for
![]() $\alpha _0 = [V]$
. For this, consider the composition of maps
$\alpha _0 = [V]$
. For this, consider the composition of maps
By the definition of the exterior product, we have
in
![]() $\mathrm {CH}_*(E\times X)$
. Then we get
$\mathrm {CH}_*(E\times X)$
. Then we get
 $$ \begin{align*} j_{*}[V] \times (c(\mathrm{id})\cdot [X]) &= (J)_*([V]\times c(\mathrm{id})\cdot [X])\\ &= (J)_*( c(p_2\circ J)\cdot [V\times X])\\ &= c(p_2)\cdot J_{*}[V\times X]\\ &= c(p_2)\cdot (j_{*}[V]\times [X]),\ \end{align*} $$
$$ \begin{align*} j_{*}[V] \times (c(\mathrm{id})\cdot [X]) &= (J)_*([V]\times c(\mathrm{id})\cdot [X])\\ &= (J)_*( c(p_2\circ J)\cdot [V\times X])\\ &= c(p_2)\cdot J_{*}[V\times X]\\ &= c(p_2)\cdot (j_{*}[V]\times [X]),\ \end{align*} $$
where the second equality follows from the proven case in equation (56) and the third equality follows from the compatibility of proper pushforward. Using equation (55), we then have
 $$ \begin{align*} \varphi_B^!\left(\alpha\times (c(\mathrm{id})\cdot [X])\right) &= \varphi_B^!\left(c(p_2)\cdot (\alpha\times [X])\right)\\ &= c(\varphi)\cdot\varphi_B^!\left(\alpha\times [X]\right) = c(\varphi)\cdot \alpha, \end{align*} $$
$$ \begin{align*} \varphi_B^!\left(\alpha\times (c(\mathrm{id})\cdot [X])\right) &= \varphi_B^!\left(c(p_2)\cdot (\alpha\times [X])\right)\\ &= c(\varphi)\cdot\varphi_B^!\left(\alpha\times [X]\right) = c(\varphi)\cdot \alpha, \end{align*} $$
which proves the theorem.
The above theorem gives the commutativity of the operational Chow group under assumptions.
Corollary C.7. Let X be an algebraic stack stratified by global quotient stacks.
-
a) When X is smooth over k,
 $\mathrm {CH}_{\mathrm {OP}}^*(X)_{\mathbb {Q}}$
is a commutative ring.
$\mathrm {CH}_{\mathrm {OP}}^*(X)_{\mathbb {Q}}$
is a commutative ring. -
b) When
 $\mathrm {char} (k)=0$
,
$\mathrm {char} (k)=0$
,
 $\mathrm {CH}_{\mathrm {OP}}^*(X)_{\mathbb {Q}}$
is a commutative ring.
$\mathrm {CH}_{\mathrm {OP}}^*(X)_{\mathbb {Q}}$
is a commutative ring.
Proof. We adapt the proof of [Reference FultonFul98, Example 17.4.4]. Part a) is a direct consequence of Theorem C.6 since the intersection product of [Reference KreschKre99] is commutative:
for
![]() $\alpha , \beta \in \mathrm {CH}_*(X)$
and where
$\alpha , \beta \in \mathrm {CH}_*(X)$
and where
![]() $\Delta : X \to X \times X$
is the diagonal, which is invariant under switching the factors of
$\Delta : X \to X \times X$
is the diagonal, which is invariant under switching the factors of
![]() $X \times X$
.
$X \times X$
.
The proof of b) relies on the functorial resolution of singularities. When
![]() $\mathrm {char} (k)=0$
, the resolution of singularities can be done functorially with respect to smooth morphisms; see [Reference Encinas and VillamayorEV98]. Therefore we can find a smooth stack
$\mathrm {char} (k)=0$
, the resolution of singularities can be done functorially with respect to smooth morphisms; see [Reference Encinas and VillamayorEV98]. Therefore we can find a smooth stack
![]() $\tilde {X}$
and a representable, surjective, birational morphism
$\tilde {X}$
and a representable, surjective, birational morphism
![]() $p: \widetilde {X}\to X$
. Since X is stratified by global quotient stacks and p is representable,
$p: \widetilde {X}\to X$
. Since X is stratified by global quotient stacks and p is representable,
![]() $\widetilde {X}$
is also stratified by global quotient stacks. Therefore the commutativity of
$\widetilde {X}$
is also stratified by global quotient stacks. Therefore the commutativity of
![]() $\mathrm {CH}_{\mathrm {OP}}^*(X)_{\mathbb {Q}}$
follows because the pullback
$\mathrm {CH}_{\mathrm {OP}}^*(X)_{\mathbb {Q}}$
follows because the pullback
![]() $p^*$
on
$p^*$
on
![]() $\mathrm {CH}_{\mathrm {OP}}^*(-)_{\mathbb {Q}}$
is injective.
$\mathrm {CH}_{\mathrm {OP}}^*(-)_{\mathbb {Q}}$
is injective.
When k is a perfect field, the commutativity of rational operational Chow groups of schemes follows from de Jong’s alteration ([Reference de JongdJ96]). However, the authors do not know whether a functorial (with respect to smooth morphisms) construction of alteration is possible. Hence we cannot prove for now the commutativity of operational Chow groups for algebraic stacks over a perfect field of positive characteristic.
However, we note that nonetheless, all results and formulas concerning tautological classes discussed in the main text are valid over arbitrary fields. Indeed, the operational classes only appear in intermediate steps of some of the computations, and while these contain some examples of non-smooth spaces (like the universal curve over the space
![]() $\mathfrak {M}_{\Gamma }$
), we are never in the position of having to exchange orders of multiplication of operational classes on these singular spaces.
$\mathfrak {M}_{\Gamma }$
), we are never in the position of having to exchange orders of multiplication of operational classes on these singular spaces.
In the main part of the paper, we use Theorem C.6 above to realize tautological classes in
![]() $\mathrm {CH}_*(\mathfrak {M}_{g,n,a})$
as operational Chow classes. The following lemma is then useful when doing calculus between tautological classes.
$\mathrm {CH}_*(\mathfrak {M}_{g,n,a})$
as operational Chow classes. The following lemma is then useful when doing calculus between tautological classes.
Lemma C.8. Consider the following commutative diagram

where all stacks are locally of finite type over k, equidimensional and stratified by global quotient stacks and the square in the middle is a Cartesian square. Suppose f is representable, proper and
![]() $\pi $
is representable, proper, flat and p is representable, proper, birational. For
$\pi $
is representable, proper, flat and p is representable, proper, birational. For
![]() $\alpha \in \mathrm {CH}_{\mathrm {OP}}^*(X)$
,
$\alpha \in \mathrm {CH}_{\mathrm {OP}}^*(X)$
,
Proof. Using the compatibility of proper pushforward and flat pullback of the cycle
![]() $\alpha \cap [X]$
in
$\alpha \cap [X]$
in
![]() $\mathrm {CH}_*(X,\mathbb {Q})$
and the fact that, by definition,
$\mathrm {CH}_*(X,\mathbb {Q})$
and the fact that, by definition,
![]() $\alpha $
is compatible with flat pullback by
$\alpha $
is compatible with flat pullback by
![]() $\pi '$
, we have
$\pi '$
, we have
 $$ \begin{align*} \pi^* f_* (\alpha \cap [X]) &= f^{\prime}_*(\pi')^* (\alpha \cap [X])\\ &= f^{\prime}_* \left( ((\pi')^*\alpha) \cap (\pi')^*[X] \right)\\ &= f^{\prime}_* \left( ((\pi')^*\alpha) \cap [W] \right). \end{align*} $$
$$ \begin{align*} \pi^* f_* (\alpha \cap [X]) &= f^{\prime}_*(\pi')^* (\alpha \cap [X])\\ &= f^{\prime}_* \left( ((\pi')^*\alpha) \cap (\pi')^*[X] \right)\\ &= f^{\prime}_* \left( ((\pi')^*\alpha) \cap [W] \right). \end{align*} $$
Since
![]() $p_*[U]=W$
, we use the projection formula for the proper morphism p and obtain
$p_*[U]=W$
, we use the projection formula for the proper morphism p and obtain
 $$ \begin{align*} f^{\prime}_* \left( ((\pi')^*\alpha) \cap [W] \right) &= f^{\prime}_* \left( ((\pi')^*\alpha) \cap p_*[U] \right)\\ &=f^{\prime}_* \left( p_* \left( (p^* (\pi')^*\alpha) \cap [U] \right)\right)\\ &=r_* (s^*\alpha) \cap [U]. \end{align*} $$
$$ \begin{align*} f^{\prime}_* \left( ((\pi')^*\alpha) \cap [W] \right) &= f^{\prime}_* \left( ((\pi')^*\alpha) \cap p_*[U] \right)\\ &=f^{\prime}_* \left( p_* \left( (p^* (\pi')^*\alpha) \cap [U] \right)\right)\\ &=r_* (s^*\alpha) \cap [U]. \end{align*} $$
This proves the identity.
We conclude the section by comparing the approach to operational classes above to the one taken in the paper [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20]. This paper studies the intersection theory of the universal Picard stack
![]() $\mathfrak {Pic}_{g,n}$
of the universal curve
$\mathfrak {Pic}_{g,n}$
of the universal curve
![]() $\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
. However, instead of studying the operational Chow classes defined above, this paper considers operational Chow groups
$\mathfrak {C}_{g,n} \to \mathfrak {M}_{g,n}$
. However, instead of studying the operational Chow classes defined above, this paper considers operational Chow groups
![]() $\mathrm {CH}^*_{\text {op}}(\mathfrak {Pic}_{g,n})$
where the test spaces
$\mathrm {CH}^*_{\text {op}}(\mathfrak {Pic}_{g,n})$
where the test spaces
![]() $B \to X$
are restricted to be finite type schemes. A class
$B \to X$
are restricted to be finite type schemes. A class
![]() $c \in \mathrm {CH}^p_{\text {op}}(X)$
on a locally finite type algebraic stack X over k is a collection of operations
$c \in \mathrm {CH}^p_{\text {op}}(X)$
on a locally finite type algebraic stack X over k is a collection of operations
for every morphism
![]() $\varphi : B \to X$
, where B is a scheme of finite type over k, satisfying compatibility conditions as in Definition C.1; see [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Definition 10] for details. We have comparison maps between
$\varphi : B \to X$
, where B is a scheme of finite type over k, satisfying compatibility conditions as in Definition C.1; see [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Definition 10] for details. We have comparison maps between
![]() $\mathrm {CH}_{\mathrm {OP}}^*, \mathrm {CH}^*_{\text {op}}$
and
$\mathrm {CH}_{\mathrm {OP}}^*, \mathrm {CH}^*_{\text {op}}$
and
![]() $\mathrm {CH}^*$
.Footnote
21
As explained in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Section 2.3], for X smooth, equidimensional and admitting a stratification by global quotient stacks, there exists a natural map
$\mathrm {CH}^*$
.Footnote
21
As explained in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Section 2.3], for X smooth, equidimensional and admitting a stratification by global quotient stacks, there exists a natural map
On the other hand, for any algebraic stack X, there exists a natural map
defined by the restriction. The following statement is a direct consequence of Theorem C.6.
Corollary C.9. When X is an equidimensional smooth Deligne-Mumford stack over k, the comparison maps in equations (57) and (58) are isomorphisms.
Proof. Indeed, for the two maps
we have that the first is an isomorphism by Theorem C.6 and the composition is an isomorphism by [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20, Lemma 15], and thus the second map must also be an isomorphism.
Acknowledgments
We are indebted to Andrew Kresch for many stimulating conversations and considerable help and input concerning Chow groups of algebraic stacks. We are also grateful to Jakob Oesinghaus, Rahul Pandharipande and Rachel Webb for many interesting conversations. Finally, we want to thank the anonymous referee for an exceptionally thorough reading of the first version of this paper and numerous comments and suggestions that have helped to both improve the presentation as well as clarify several technical issues.
Conflicts of Interest
None.
Financial Support
Y. B. was supported by ERC Grant ERC-2017-AdG-786580-MACI and Korea Foundation for Advanced Studies (KFAS). J. S. was supported by the Early Postdoc.Mobility grant 184245 and grant 184613 of the Swiss National Science Foundation and thanks the Max Planck Institute for Mathematics in Bonn for its hospitality.
The project has received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation program (grant agreement No. 786580).