Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-09T08:46:28.288Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CHERN–SCHWARTZ–MACPHERSON CLASS OF AN EMBEDDABLE SCHEME

Part of: Surfaces and higher-dimensional varieties Cycles and subschemes

Published online by Cambridge University Press:  18 September 2019

PAOLO ALUFFI
PAOLO ALUFFI*
Affiliation:
Mathematics Department, Florida State University, Tallahassee FL 32306, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Chern–Schwartz–MacPherson class of a hypersurface in a nonsingular variety may be computed directly from the Segre class of the Jacobian subscheme of the hypersurface; this has been known for a number of years. We generalize this fact to arbitrary embeddable schemes: for every subscheme 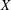$X$ of a nonsingular variety 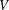$V$, we define an associated subscheme 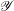$\mathscr{Y}$ of a projective bundle 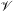$\mathscr{V}$ over 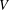$V$ and provide an explicit formula for the Chern–Schwartz–MacPherson class of 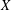$X$ in terms of the Segre class of 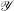$\mathscr{Y}$ in 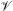$\mathscr{V}$. If 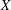$X$ is a local complete intersection, a version of the result yields a direct expression for the Milnor class of 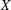$X$.

For 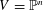$V=\mathbb{P}^{n}$, we also obtain expressions for the Chern–Schwartz–MacPherson class of 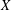$X$ in terms of the ‘Segre zeta function’ of 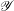$\mathscr{Y}$.

MSC classification

Primary: 14C17: Intersection theory, characteristic classes, intersection multiplicities
Secondary: 14J17: Singularities
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e30
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2019

References

Aluffi, P. and Esole, M., ‘Chern class identities from tadpole matching in type IIB and F-theory’, J. High Energy Phys. (3) (2009), 032 29.Google Scholar
Aluffi, P., ‘Characteristic classes of discriminants and enumerative geometry’, Comm. Algebra 26(10) (1998), 3165–3193.Google Scholar
Aluffi, P., ‘Chern classes for singular hypersurfaces’, Trans. Amer. Math. Soc. 351(10) (1999), 3989–4026.Google Scholar
Aluffi, P., ‘Computing characteristic classes of projective schemes’, J. Symbolic Comput. 35(1) (2003), 3–19.Google Scholar
Aluffi, P., ‘Characteristic classes of singular varieties’, inTopics in Cohomological Studies of Algebraic Varieties, Trends in Mathematics (Birkhäuser, Basel, 2005), 1–32.Google Scholar
Aluffi, P., ‘Limits of Chow groups, and a new construction of Chern–Schwartz–MacPherson classes’, Pure Appl. Math. Q. 2(4) (2006), 915–941.Google Scholar
Aluffi, P., ‘Euler characteristics of general linear sections and polynomial Chern classes’, Rend. Circ. Mat. Palermo (2) 62(1) (2013), 3–26.Google Scholar
Aluffi, P., ‘The Segre zeta function of an ideal’, Adv. Math. 320 (2017), 1201–1226.Google Scholar
Aluffi, P., ‘MacPherson’s and Fulton’s Chern classes of hypersurfaces’, Int. Math. Res. Not. IMRN (11) (1994), 455–465.Google Scholar
Aluffi, P. and Mihalcea, L. C., ‘Chern classes of Schubert cells and varieties’, J. Algebraic Geom. 18(1) (2009), 63–100.Google Scholar
Aluffi, P. and Mihalcea, L. C., ‘Chern–Schwartz–MacPherson classes for Schubert cells in flag manifolds’, Compos. Math. 152(12) (2016), 2603–2625.Google Scholar
Aluffi, P., Mihalcea, L. C., Schürmann, J. and Su, C., ‘Shadows of characteristic cycles, Verma modules, and positivity of Chern–Schwartz–MacPherson classes of Schubert cells’. Preprint, 2017, arXiv:1709.08697.Google Scholar
Brasselet, J.-P., Lehmann, D., Seade, J. and Suwa, T., ‘Milnor classes of local complete intersections’, Trans. Amer. Math. Soc. 354(4) (2002), 1351–1371 (electronic).Google Scholar
Brasselet, J.-P. and Schwartz, M.-H., ‘Sur les classes de Chern d’un ensemble analytique complexe’, inThe Euler–Poincaré Characteristic (French), Astérisque, 83 (Soc. Math. France, Paris, 1981), 93–147.Google Scholar
Callejas-Bedregal, R., Morgado, M. F. Z. and Seade, J., ‘On the Milnor classes of local complete intersections’. Preprint, 2012, arXiv:1208.5084, retrieved 5/28/2018.Google Scholar
Cappell, S. E., Maxim, L., Schürmann, J. and Shaneson, J. L., ‘Characteristic classes of complex hypersurfaces’, Adv. Math. 225(5) (2010), 2616–2647.Google Scholar
Cukierman, F., Soares, M. G. and Vainsencher, I., ‘Singularities of logarithmic foliations’, Compos. Math. 142(1) (2006), 131–142.Google Scholar
Fehér, L. and Rimányi, R., ‘Chern–Schwartz–MacPherson classes of degeneracy loci’, Geom. Topol. 22(6) (2018), 3575–3622.Google Scholar
Feher, L. M., Rimanyi, R. and Weber, A., ‘Characteristic classes of orbit stratifications, the axiomatic approach’. Preprint, 2018, arXiv:1811.11467.Google Scholar
Fullwood, J., ‘On Milnor classes via invariants of singular subschemes’, J. Singul. 8 (2014), 1–10.Google Scholar
Fulton, W., Intersection Theory, (Springer, Berlin, 1984).Google Scholar
Fullwood, J. and Wang, D., ‘Towards a simple characterization of the Chern–Schwartz–MacPherson class’. Preprint, 2016, arXiv:1604.07954.Google Scholar
Grayson, D. R. and Stillman, M. E., ‘Macaulay2, a software system for research in algebraic geometry’. Available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Hartshorne, R., Algebraic Geometry, (Springer, New York, 1977).Google Scholar
Helmer, M., ‘Algorithms to compute the topological Euler characteristic, Chern–Schwartz–MacPherson class and Segre class of projective varieties’, J. Symbolic Comput. 73 (2016), 120–138.Google Scholar
Helmer, M., ‘Computing characteristic classes of subschemes of smooth toric varieties’, J. Algebra 476 (2017), 548–582.Google Scholar
Helmer, M., ‘A direct algorithm to compute the topological Euler characteristic and Chern–Schwartz–MacPherson class of projective complete intersection varieties’, Theoret. Comput. Sci. 681 (2017), 54–74.Google Scholar
Helmer, M. and Jost, C., ‘CharacteristicClasses.m2, a Macaulay2 package’.Google Scholar
Jorgenson, G., ‘A relative Segre zeta function’. Preprint, 2019, arXiv:1906.09651.Google Scholar
Jost, C., ‘Computing characteristic classes and the topological Euler characteristic of complex projective schemes’, J. Softw. Algebra Geom. 7 (2015), 31–39.Google Scholar
Kennedy, G., ‘MacPherson’s Chern classes of singular algebraic varieties’, Comm. Algebra 18(9) (1990), 2821–2839.Google Scholar
Liao, X., ‘An approach to Lagrangian specialization via MacPherson’s graph construction’. Preprint, 2018, arXiv:1808.09606.Google Scholar
MacPherson, R. D., ‘Chern classes for singular algebraic varieties’, Ann. of Math. (2) 100 (1974), 423–432.Google Scholar
Marco-Buzunáriz, M. A., ‘A polynomial generalization of the Euler characteristic for algebraic sets’, J. Singul. 4 (2012), 114–130.Google Scholar
Maxim, L., Saito, M. and Schürmann, J., ‘Hirzebruch–Milnor classes of complete intersections’, Adv. Math. 241 (2013), 220–245.Google Scholar
Ohmoto, T., ‘Thom polynomial and Milnor number for isolated complete intersection singularities’. Preprint.Google Scholar
Parusiński, A. and Pragacz, P., ‘Chern–Schwartz–MacPherson classes and the Euler characteristic of degeneracy loci and special divisors’, J. Amer. Math. Soc. 8(4) (1995), 793–817.Google Scholar
Parusiński, A. and Pragacz, P., ‘Characteristic classes of hypersurfaces and characteristic cycles’, J. Algebraic Geom. 10(1) (2001), 63–79.Google Scholar
Rimányi, R. and Varchenko, A., ‘Equivariant Chern–Schwartz–MacPherson classes in partial flag varieties: interpolation and formulae’, inSchubert Varieties, Equivariant Cohomology and Characteristic Classes—IMPANGA 15, EMS Series of Congress Reports (European Mathematical Society, Zürich, 2018), 225–235.Google Scholar
Schwartz., M.-H., ‘Classes caractéristiques définies par une stratification d’une variété analytique complexe. I’, C. R. Math. Acad. Sci. Paris 260 (1965), 3262–3264.Google Scholar
Schwartz, M.-H., ‘Classes caractéristiques définies par une stratification d’une variété analytique complexe. II’, C. R. Math. Acad. Sci. Paris 260 (1965), 3535–3537.Google Scholar
Yokura, S., ‘On a Verdier-type Riemann–Roch for Chern–Schwartz–MacPherson class’, Topology Appl. 94(1–3) (1999), 315–327.Google Scholar
Yokura, S., ‘On characteristic classes of complete intersections’, inAlgebraic Geometry: Hirzebruch 70 (Warsaw, 1998), Contemporary Mathematics, 241 (American Mathematical Society, Providence, RI, 1999), 349–369.Google Scholar
Yokura, S., ‘Motivic Milnor classes’, J. Singul. 1 (2010), 39–59.Google Scholar
Zhang, X., ‘Chern classes and characteristic cycles of determinantal varieties.’, J. Algebra 497 (2018), 55–91.Google Scholar