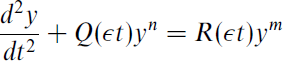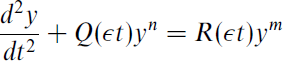An unforced oscillator which obeys the equation x¨+α (x2+x˙2−1)x˙+x=0 has a pure sine-wave limit cycle which is attained rapidly for a range of values of α. In this paper, free and forced oscillation of this equation are examined experimentally and compared with those for the Van der Pol oscillator. Asymptotic solutions for small α confirm the experimental results.

Analysing the motion of a driven, damped pendulum as a function of the amplitude of the driving force, we show, first, that for moderate values and larger of the amplitude, deviations from a simple motion with the period of the driving force are bounded by a constant times the inverse square root of the amplitude, for late times. For amplitudes above a larger threshold we are able to show that, for late times, the motion becomes a periodic motion with the period of the driving force. The manner in which this periodic motion is achieved with the passage of time is analysed.

The scattering of high-frequency sound waves by two-dimensional curved boundaries has received much attention over the past few decades, with particular interest in the effects of tangential ray incidence. In the event that the radius of curvature is not small, an analysis near the point of tangency gives rise to the Fock–Leontovič equation for the local field amplitude which, in turn, matches the creeping field of Keller's geometrical theory of diffraction. If the radius of curvature is sufficiently small, however, then this analysis is not valid and it is necessary to solve the full Helmholtz equation in the presence of a parabolic boundary. Under these conditions, which are canonical for diffraction by a sufficiently slender body, results are presented for the case of a plane wave impinging upon an acoustically hard parabolic cylinder. This diffraction process engenders a creeping field at one tip of the slender body, which then propagates around the body to the other tip. Here its energy is partially reflected, partially transmitted and partially radiated out in a detached field. A full description of this is given, along with a discussion of the ‘blunt’ limit in which we show that not only do we get the traditional creeping field of Keller's geometrical theory of diffraction, but also an exponentially small backward-propagating creeping field not predicted by traditional ray methods.

Formal hyperasymptotic expansions of integrals are obtained from the Poincaré asymptotic expansion by re-expanding the remainder term. We show that for the integrals under consideration these hyperasymptotic expansions can be made accurate to any desired exponentially-small order.

In a recent paper, the author showed that for certain symmetric bisuperlinear equations, cosine-like boundary behaviours will not yield symmetric solutions [1]. In this paper, we attack the adiabatic invariant problem by showing that, for these strongly nonlinear oscillators, the adiabatic invariant is intimately related to z′(0;∈) for a family of solutions.

This paper addresses short-time existence and uniqueness of a solution to the N-dimensional Hele–Shaw flow problem with surface tension as driving mechanism. Global existence in time and exponential decay of the solution near equilibrium are also proved. The results are obtained in Sobolev spaces Hs with sufficiently large s. The main tools are perturbations of a fixed reference domain, linearization with respect to these perturbations, a quasilinearization argument based on a geometric invariance property, and a priori energy estimates.